Natural Science
Vol.6 No.6(2014), Article ID:44854,12 pages DOI:10.4236/ns.2014.66040
Generalized Lagrange Structure of Deformed Minkowski Spacetime
Roberto Mignani1,2,3, Fabio Cardone2,4, Andrea Petrucci5
1Dipartimento di Matematica e Fisica, Sezione di Fisica, Università degli Studi “Roma Tre”, Roma, Italy
2GNFM, Istituto Nazionale di Alta Matematica “F.Severi”, Città Universitaria, Roma, Italy
3I.N.F.N.-Sezione di Roma III, Roma, Italy
4Istituto per lo Studio dei Materiali Nanostrutturati, (ISMN-CNR), Roma, Italy
5ENEA, Italian National Agency for New Technologies, Energy and Sustainable Economic Development, Roma, Italy
Email: mignani@fis.uniroma3.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 4 December 2013; revised 4 January 2014; accepted 11 January 2014
ABSTRACT
We discuss the generalized Lagrange structure of a deformed Minkowski space (DMS), 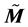 , namely a (four-dimensional) generalization of the (local) space-time based on an energy-dependent “deformation” of the usual Minkowski geometry. In
, namely a (four-dimensional) generalization of the (local) space-time based on an energy-dependent “deformation” of the usual Minkowski geometry. In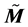 , local Lorentz invariance is naturally violated, due to the energy dependence of the deformed metric. Moreover, the generalized Lagrange structure of
, local Lorentz invariance is naturally violated, due to the energy dependence of the deformed metric. Moreover, the generalized Lagrange structure of 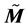 allows one to endow the deformed space-time with both curvature and torsion.
allows one to endow the deformed space-time with both curvature and torsion.
Keywords:Deformed Space-Time, Lorentz Invariance, Generalized Lagrange Space

1. Introduction
It is well known that symmetries play a basic role in all fields of physics. In particular, in relativity the most fundamental symmetry is local Lorentz invariance (LLI). Over the last two decades there have been tremendous interest and progress in testing LLI [1] [2] although theoretical speculations on LLI violation can be traced back to the early sixties of the past century. The theoretical formalisms admitting for LLI breakdown can be roughly divided in two classes: unified theories and theories with modified spacetimes.
A formalism of this second kind is Deformed Special Relativity (DSR), namely a (four-dimensional) generalization of the (local) space-time structure based on an energy-dependent “deformation” of the usual Minkowski geometry [3] [4] . As we shall see, the energy-dependence of the deformed metric in DSR gives rise to a natural violation of the standard Lorentz invariance. However, LLI can be recovered in a wider, generalized sense. Moreover, the deformed Minkowski space (DMS) 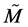 can be shown to be endowed with an additional geometrical structure, that of Generalized Lagrange Space. This allows one to define in
can be shown to be endowed with an additional geometrical structure, that of Generalized Lagrange Space. This allows one to define in 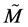 both curvature and torsion.
both curvature and torsion.
The paper is organized as follows. In Section 2, we review the basic features of DSR that are relevant to our purposes. Lorentz violation in DSR is discussed in Subsect. 2.2. Section 3 deals with the generalized Lagrange structure of . Conclusions and perspectives are given in Section 4.
. Conclusions and perspectives are given in Section 4.
2. Elements of Deformed Special Relativity
2.1. Energy and Geometry
The geometrical structure of the physical world-both at a large and a small scale—has been debated since a long. After Einstein, the generally accepted view considers the arena of physical phenomena as a four-dimensional space-time, endowed with a global, curved, Riemannian structure and a local, flat, Minkowskian geometry.
However, an analysis of some experimental data concerning physical phenomena ruled by different fundamental interactions have provided evidence for a local departure from Minkowski metric [3] [4] : among them, the lifetime of the (weakly decaying) 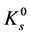 meson, the Bose-Einstein correlation in (strong) pion production and the superluminal propagation of electromagnetic waves in waveguides. These phenomena seemingly show a (local) breakdown of Lorentz invariance, together with a plausible inadequacy of the Minkowski metric; on the other hand, they can be interpreted in terms of a deformed Minkowski spacetime, with metric coefficients depending on the energy of the process considered [3] [4] .
meson, the Bose-Einstein correlation in (strong) pion production and the superluminal propagation of electromagnetic waves in waveguides. These phenomena seemingly show a (local) breakdown of Lorentz invariance, together with a plausible inadequacy of the Minkowski metric; on the other hand, they can be interpreted in terms of a deformed Minkowski spacetime, with metric coefficients depending on the energy of the process considered [3] [4] .
All the above facts suggested to introduce a (four-dimensional) generalization of the (local) space-time structure based on an energy-dependent “deformation” of the usual Minkowski geometry of M, whereby the corresponding deformed metrics ensuing from the fit to the experimental data seem to provide an effective dynamical description of the relevant interactions (at the energy scale and in the energy range considered).
An analogous energy-dependent metric seems to hold for the gravitational field (at least locally, i.e. in a neighborhood of Earth) when analyzing some classical experimental data concerning the slowing down of clocks.
Let us shortly review the main ideas and results concerning the (four-dimensional) deformed Minkowski spacetime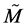 .
.
The four-dimensional “ deformed” metric scheme is based on the assumption that spacetime, in a preferred frame which is fixed by the scale of energy  , is endowed with a metric of the form
, is endowed with a metric of the form
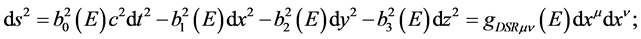 (1)
(1)
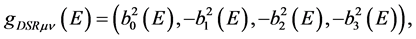 (2)
(2)
with 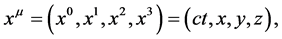
![]() being the usual speed of light in vacuum. We named “Deformed Special Relativity” (DSR) the relativity theory built up on metric (1), (2).
being the usual speed of light in vacuum. We named “Deformed Special Relativity” (DSR) the relativity theory built up on metric (1), (2).
Metric (1), (2) is supposed to hold locally, i.e. in the spacetime region where the process occurs. It is supposed moreover to play a dynamical role, and to provide a geometric description of the interaction considered. In this sense, DSR realizes the so called “Finzi Principle of Solidarity” between space-time and phenomena occurring in it1 (see [5] ). Futhermore, we stress that, from the physical point of view, 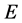 is the measured energy of the system, and thus a merely phenomenological (non-metric) variable2.
is the measured energy of the system, and thus a merely phenomenological (non-metric) variable2.
We notice explicitly that the spacetime  described by (1), (2) is flat (it has zero four-dimensional curvature, at least at this level; but see below), so that the geometrical description of the fundamental interactions based on it differs from the general relativistic one (whence the name “deformation” used to characterize such a situation). Although for each interaction the corresponding metric reduces to the Minkowskian one for a suitable value of the energy
described by (1), (2) is flat (it has zero four-dimensional curvature, at least at this level; but see below), so that the geometrical description of the fundamental interactions based on it differs from the general relativistic one (whence the name “deformation” used to characterize such a situation). Although for each interaction the corresponding metric reduces to the Minkowskian one for a suitable value of the energy 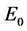 (which is characteristic of the interaction considered), the energy of the process is fixed and cannot be changed at will. Thus, in spite of the fact that formally it would be possible to recover the usual Minkowski space
(which is characteristic of the interaction considered), the energy of the process is fixed and cannot be changed at will. Thus, in spite of the fact that formally it would be possible to recover the usual Minkowski space 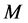 by a suitable change of coordinates (e.g. by a rescaling), this would amount, in such a framework, to be a mere mathematical operation devoid of any physical meaning.
by a suitable change of coordinates (e.g. by a rescaling), this would amount, in such a framework, to be a mere mathematical operation devoid of any physical meaning.
As far as phenomenology is concerned, it is important to recall that a local breakdown of Lorentz invariance may be envisaged for all the four fundamental interactions (electromagnetic, weak, strong and gravitational) whereby one gets evidence for a departure of the spacetime metric from the Minkowskian one (in the energy range examined). The explicit functional form of the metric (2) for all the four interactions can be found in [3] [4] . Here, we confine ourselves to recall the following basic features of these energy-dependent phenomenological metrics:
1) Both the electromagnetic and the weak metric show the same functional behavior, namely
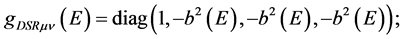 (3)
(3)
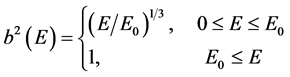 (4)
(4)
with the only difference between them being the threshold energy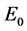 , i.e. the energy value at which the metric parameters are constant, i.e. the metric becomes Minkowskian; the fits to the experimental data yield
, i.e. the energy value at which the metric parameters are constant, i.e. the metric becomes Minkowskian; the fits to the experimental data yield
![]() (5)
(5)
2) for strong and gravitational interactions, the metrics read:
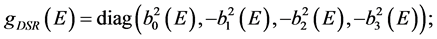 (6)
(6)
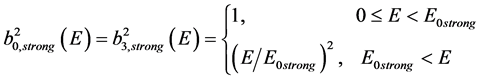
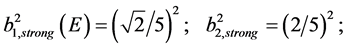 (7)
(7)
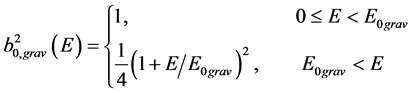 (7’)
(7’)
with
![]() (8)
(8)
Let us stress that, in this case, contrarily to the electromagnetic and the weak ones, a deformation of the time coordinate occurs; moreover, the three-space is anisotropic3, with two spatial parameters constant (but different in value) and the third one variable with energy in an “over-Minkowskian” way (namely it reaches the limit of Minkowskian metric for decreasing values of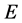 , with
, with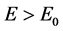 ) [3] [4] .
) [3] [4] .
As a final remark, we stress that actually the four-dimensional energy-dependent spacetime  is just a manifestation of a larger, five-dimensional space in which energy plays the role of a fifth dimension. Indeed, it can be shown that the physics of the interaction lies in the curvature of such a five-dimensional spacetime, in which the four-dimensional, deformed Minkowski space is embedded. Moreover, all the phenomenological metrics (2), (3) and (5), (6) can be obtained as solutions of the vacuum Einstein equations in this generalized Kaluza-Klein scheme [3] [4] .
is just a manifestation of a larger, five-dimensional space in which energy plays the role of a fifth dimension. Indeed, it can be shown that the physics of the interaction lies in the curvature of such a five-dimensional spacetime, in which the four-dimensional, deformed Minkowski space is embedded. Moreover, all the phenomenological metrics (2), (3) and (5), (6) can be obtained as solutions of the vacuum Einstein equations in this generalized Kaluza-Klein scheme [3] [4] .
2.2. Breakdown of Standard LLI Invariance in DSR
Let us remark the mathematically self-evident, but physically basic, point that the generalized metric (2) (and the corresponding interval (1)) is clearly not preserved by the usual Lorentz transformations. If 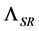 is the
is the 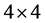 matrix representing a standard Lorentz transformation, this amounts to say that the similarity transformation generated by
matrix representing a standard Lorentz transformation, this amounts to say that the similarity transformation generated by 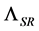 does not leave the deformed metric tensor
does not leave the deformed metric tensor 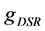 invariant:
invariant:
 (9)
(9)
(where 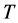 denotes transpose) namely, standard Lorentz invariance is violated.
denotes transpose) namely, standard Lorentz invariance is violated.
However, in DSR it is possible to introduce generalized Lorentz transformations which are the isometries of the deformed Minkowski space 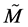 [3] [4] . They are also referred to as deformed Lorentz transformations (DLT). If
[3] [4] . They are also referred to as deformed Lorentz transformations (DLT). If 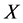 denotes a column four-vector, a DLT is therefore a
denotes a column four-vector, a DLT is therefore a 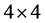 matrix
matrix 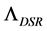 connecting two inertial frames
connecting two inertial frames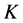 ,
, 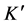
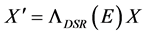 (10)
(10)
and leaving the deformed interval (1) invariant, namely
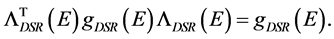 (11)
(11)
Therefore, unlike the case of a standard LT, a deformed Lorentz transformation generates a similarity transformation which preserves the deformed metric tensor. Let us also notice the explicit dependence of  on the energy
on the energy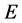 . This means that in DSR Lorentz invariance is recovered, although in a generalized sense.
. This means that in DSR Lorentz invariance is recovered, although in a generalized sense.
The explicit form of the deformed Lorentz transformations can be found in [3] [4] .
2.3. DSR as Metric Gauge Theory
It is clear from the discussion of the phenomenological metrics describing the four fundamental interactions in DSR that the Minkowski space 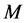 is the space-time manifold of background of any experimental measurement and detection (namely, of any process of acquisition of information on physical reality). In particular, we can consider this Minkowski space as that associated to the electromagnetic interaction above the threshold energy
is the space-time manifold of background of any experimental measurement and detection (namely, of any process of acquisition of information on physical reality). In particular, we can consider this Minkowski space as that associated to the electromagnetic interaction above the threshold energy![]() . Therefore, in modeling the physical phenomena, one has to take into account this fact. The geometrical nature of interactions, i.e. assuming the validity of the Finzi principle, means that one has to suitably gauge (with reference to M) the space-time metrics with respect to the interaction-and/or the phenomenon-under study. In other words, one needs to “adjust” suitably the local metric of space-time according to the interaction acting in the region considered. We can name such a procedure “Metric Gaugement Process” (M.G.P.). Like in usual gauge theories a different phase is chosen in different space-time points, in DSR different metrics are associated to different space-time manifolds according to the interaction acting therein. We have thus a gauge structure on the space of manifolds
. Therefore, in modeling the physical phenomena, one has to take into account this fact. The geometrical nature of interactions, i.e. assuming the validity of the Finzi principle, means that one has to suitably gauge (with reference to M) the space-time metrics with respect to the interaction-and/or the phenomenon-under study. In other words, one needs to “adjust” suitably the local metric of space-time according to the interaction acting in the region considered. We can name such a procedure “Metric Gaugement Process” (M.G.P.). Like in usual gauge theories a different phase is chosen in different space-time points, in DSR different metrics are associated to different space-time manifolds according to the interaction acting therein. We have thus a gauge structure on the space of manifolds
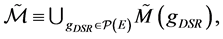 (12)
(12)
where 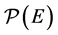 is the set of the energy-dependent pseudoeuclidean metrics of the type (2). This is why it is possible to regard Deformed Special Relativity as a Metric Gauge Theory [6] . In this case, we can consider the related fields as external metric gauge fields.
is the set of the energy-dependent pseudoeuclidean metrics of the type (2). This is why it is possible to regard Deformed Special Relativity as a Metric Gauge Theory [6] . In this case, we can consider the related fields as external metric gauge fields.
However, let us notice that DSR can be considered as a metric gauge theory from another point of view, on account of the dependence of the metric coefficients on the energy. Actually, once the MGP has been applied, by selecting the suitable gauge (namely, the suitable functional form of the metric) according to the interaction considered (thus implementing the Finzi principle), the metric dependence on the energy implies another different gauge process. Namely, the metric is gauged according to the process under study, thus selecting the given metric, with the given values of the coefficients, suitable for the given phenomenon.
We have therefore a double metric gaugement, according, on one side, to the interaction ruling the physical phenomenon examined, and on the other side to its energy, in which the metric coefficients are the analogous of the gauge functions4.
3. Deformed Minkowski Space as Generalized Lagrange Space
We want now to show that the deformed Minkowski space  of Deformed Special Relativity does possess another well-defined geometrical structure, besides the deformed metrical one. Precisely, we will show that
of Deformed Special Relativity does possess another well-defined geometrical structure, besides the deformed metrical one. Precisely, we will show that 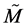 is a generalized Lagrange space [7] . As we shall see, this implies that DSR admits a different, intrinsic gauge structure.
is a generalized Lagrange space [7] . As we shall see, this implies that DSR admits a different, intrinsic gauge structure.
3.1. Generalized Lagrange Spaces
Let us give the definition of generalized Lagrange space [8] [9] , since usually one is not acquainted with it.
Consider a N-dimensional, differentiable manifold 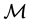 and its (N-dimensional) tangent space in a point,
and its (N-dimensional) tangent space in a point,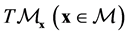 . As is well known, the union
. As is well known, the union
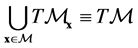 (13)
(13)
has a fibre bundle structure. Let us denote by  the generic element of
the generic element of , namely a vector tangent to
, namely a vector tangent to 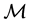 in
in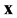 . Then, an element
. Then, an element 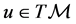 is a vector tangent to the manifold in some point
is a vector tangent to the manifold in some point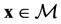 . Local coordinates for
. Local coordinates for 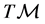 are introduced by considering a local coordinate system
are introduced by considering a local coordinate system 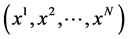 on
on 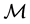 and the components of
and the components of 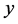 in such a coordinate system
in such a coordinate system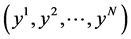 . The
. The  numbers
numbers  constitute a local coordinate system on
constitute a local coordinate system on . We can write synthetically
. We can write synthetically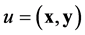 .
. 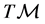 is a
is a 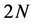 -dimensional, differentiable manifold.
-dimensional, differentiable manifold.
Let 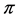 be the mapping (natural projection)
be the mapping (natural projection)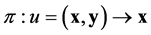 . (
. (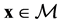 ,
,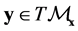 ). Then, the tern
). Then, the tern 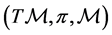 is the tangent bundle to the base manifold
is the tangent bundle to the base manifold . The image of the inverse mapping
. The image of the inverse mapping  is of course the tangent space
is of course the tangent space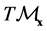 , which is called the fiber corresponding to the point
, which is called the fiber corresponding to the point  in the fiber bundle One considers also sometimes the manifold
in the fiber bundle One considers also sometimes the manifold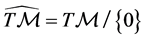 , where 0 is the zero section of the projection
, where 0 is the zero section of the projection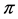 . We do not dwell further on the theory of the fiber bundles, and refer the reader to the wide and excellent literature on the subject [10] .
. We do not dwell further on the theory of the fiber bundles, and refer the reader to the wide and excellent literature on the subject [10] .
The natural basis of the tangent space  at a point
at a point 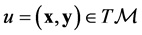 is
is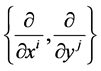 ,
,
 .
.
A local coordinate transformation in the differentiable manifold 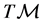 reads
reads
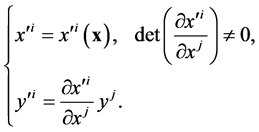 (14)
(14)
Here, 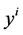 is the Liouville vector field on
is the Liouville vector field on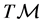 , i.e.
, i.e. .
.
On account of Equation (14), the natural basis of 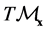 can be written as
can be written as
 (15)
(15)
Second Equation (15) shows therefore that the vector basis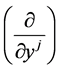 ,
, 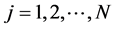 , generates a distribution
, generates a distribution
 defined everywhere on
defined everywhere on  and integrable, too (vertical distribution on
and integrable, too (vertical distribution on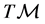 ).
).
If 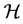 is a distribution on
is a distribution on 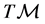 supplementary to
supplementary to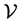 , namely
, namely
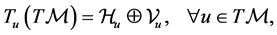 (16)
(16)
then  is called a horizontal distribution, or a nonlinear connection on
is called a horizontal distribution, or a nonlinear connection on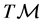 . A basis for the distributions
. A basis for the distributions
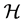 and
and  are given respectively by
are given respectively by 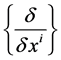 and
and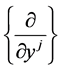 , where the basis in
, where the basis in 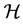 explicitly reads
explicitly reads
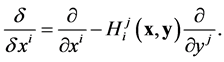 (17)
(17)
Here, 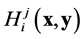 are the coefficients of the nonlinear connection
are the coefficients of the nonlinear connection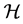 . The basis
. The basis 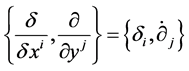 is called the adapted basis.
is called the adapted basis.
The dual basis to the adapted basis is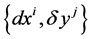 , with
, with
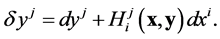 (18)
(18)
A distinguished tensor (or d-tensor) field of (r,s)-type is a quantity whose components transform like a tensor under the first coordinate transformation (19) on 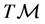 (namely they change as tensor in
(namely they change as tensor in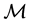 ). For instance, for a d-tensor of type (1,2):
). For instance, for a d-tensor of type (1,2):
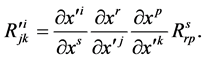 (19)
(19)
In particular, both 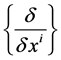 and
and 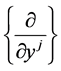 are d-(covariant) vectors, whereas
are d-(covariant) vectors, whereas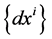 ,
, 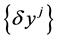 are d-(contravariant) vectors.
are d-(contravariant) vectors.
A generalized Lagrange space is a pair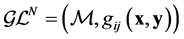 , with
, with 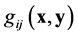 being a d-tensor of type (0,2) (covariant) on the manifold
being a d-tensor of type (0,2) (covariant) on the manifold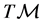 , which is symmetric, non-degenerate5 and of constant signature.
, which is symmetric, non-degenerate5 and of constant signature.
A function
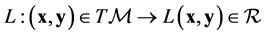 (20)
(20)
differentiable on ![]() and continuous on the null section of
and continuous on the null section of  is named a regular Lagrangian if the Hessian of
is named a regular Lagrangian if the Hessian of 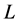 with respect to the variables
with respect to the variables 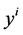 is non-singular.
is non-singular.
A generalized Lagrange space 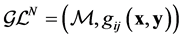 is reducible to a Lagrange space
is reducible to a Lagrange space 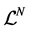 if there is a regular Lagrangian
if there is a regular Lagrangian 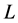 satisfying
satisfying
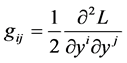 (21)
(21)
on![]() . In order that
. In order that ![]() is reducible to a Lagrange space, a necessary condition is the total symmetry of the d-tensor
is reducible to a Lagrange space, a necessary condition is the total symmetry of the d-tensor . If such a condition is satisfied, and
. If such a condition is satisfied, and ![]() are 0-homogeneous in the variables
are 0-homogeneous in the variables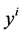 , then the function
, then the function 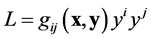 is a solution of system (21). In this case, the pair
is a solution of system (21). In this case, the pair 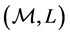 is a Finsler space6
is a Finsler space6 , with
, with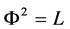 . One says that
. One says that ![]() is reducible to a Finsler space.
is reducible to a Finsler space.
Of course, ![]() reduces to a pseudo-Riemannian (or Riemannian) space
reduces to a pseudo-Riemannian (or Riemannian) space 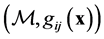 if the d-tensor
if the d-tensor 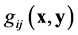 does not depend on
does not depend on . On the contrary, if
. On the contrary, if 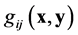 depends only on
depends only on  (at least in preferred charts), it is a generalized Lagrange space which is locally Minkowskian.
(at least in preferred charts), it is a generalized Lagrange space which is locally Minkowskian.
Since, in general, a generalized Lagrange space is not reducible to a Lagrange one, it cannot be studied by means of the methods of symplectic geometry, on which—as is well known—analytical mechanics is based.
A linear 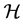 -connection on
-connection on 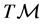 (or on
(or on![]() ) is defined by a couple of geometrical objects
) is defined by a couple of geometrical objects 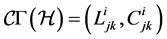 on
on 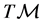 with different transformation properties under the coordinate transformation (14). Precisely,
with different transformation properties under the coordinate transformation (14). Precisely, 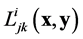 transform like the coefficients of a linear connection on
transform like the coefficients of a linear connection on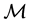 , whereas
, whereas 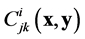 transform like a d-tensor of type (1,2).
transform like a d-tensor of type (1,2). 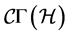 is called the metrical canonical
is called the metrical canonical 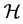 -connection of the generalized Lagrange space
-connection of the generalized Lagrange space![]() .
.
In terms of ![]() and
and ![]() one can define two kinds of covariant derivatives: a covariant horizontal (h-) derivative, denoted by “
one can define two kinds of covariant derivatives: a covariant horizontal (h-) derivative, denoted by “ ” , and a covariant vertical (v-) derivative, denoted by “
” , and a covariant vertical (v-) derivative, denoted by “ ”. For instance, for the d-tensor
”. For instance, for the d-tensor 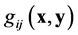 one has
one has
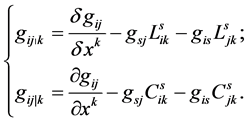 (22)
(22)
The two derivatives ![]() and
and ![]() are both d-tensors of type (0,3).
are both d-tensors of type (0,3).
The coefficients of 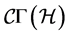 can be expressed in terms of the following generalized Christoffel symbols:
can be expressed in terms of the following generalized Christoffel symbols:
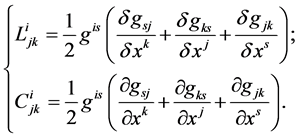 (23)
(23)
3.2. Curvature and Torsion in a Generalized Lagrange Space
By means of the connection 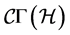 it is possible to define a d-curvature in
it is possible to define a d-curvature in  by means of the tensors
by means of the tensors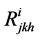 ,
, 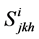 and
and 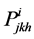 given by
given by
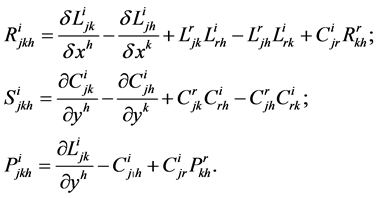 (24)
(24)
Here, the d-tensor ![]() is related to the bracket of the basis
is related to the bracket of the basis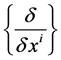 :
:
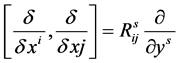 (25)
(25)
and is explicitly given by7
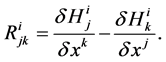 (26)
(26)
The tensor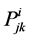 , together with
, together with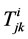 ,
, 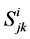 , defined by
, defined by
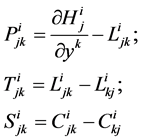 (27)
(27)
are the d-tensors of torsion of the metrical connection .
.
From the curvature tensors one can get the corresponding Ricci tensors of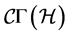 :
:
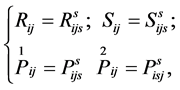 (28)
(28)
and the scalar curvatures
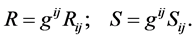 (29)
(29)
Finally, the deflection d-tensors associated to the connection 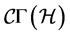 are
are
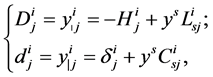 (30)
(30)
namely the hand v-covariant derivatives of the Liouville vector fields.
In the generalized Lagrange space ![]() it is possible to write the Einstein equations with respect to the canonical connection
it is possible to write the Einstein equations with respect to the canonical connection 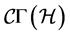 as follows:
as follows:
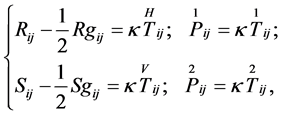 (31)
(31)
where 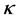 is a constant and
is a constant and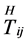 ,
, 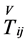 ,
, 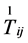 ,
, 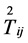 are the components of the energy-momentum tensor.
are the components of the energy-momentum tensor.
3.3. Generalized Lagrangian Structure of 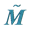
On the basis of the previous considerations, let us analyze the geometrical structure of the deformed Minkowski space of DSR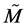 , endowed with the by now familiar metric
, endowed with the by now familiar metric 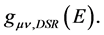 As said in Section 2,
As said in Section 2, 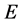 is the energy of the process measured by the detectors in Minkowskian conditions. Therefore,
is the energy of the process measured by the detectors in Minkowskian conditions. Therefore, 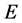 is a function of the velocity components,
is a function of the velocity components,  , where
, where 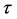 is the (Minkowskian) proper time:8
is the (Minkowskian) proper time:8
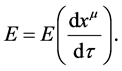 (32)
(32)
The derivatives 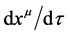 define a contravariant vector tangent to
define a contravariant vector tangent to 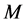 at
at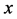 , namely they belong to
, namely they belong to . We shall denote this vector (according to the notation of the previous Subsubsection) by
. We shall denote this vector (according to the notation of the previous Subsubsection) by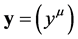 . Then,
. Then,  is a point of the tangent bundle to
is a point of the tangent bundle to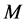 . We can therefore consider the generalized Lagrange space
. We can therefore consider the generalized Lagrange space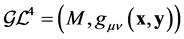 , with
, with
 (33)
(33)
Then, it is possible to prove the following theorem [7] :
The pair  is a generalized Lagrange space which is not reducible to a Riemann space, or to a Finsler space, or to a Lagrange space.
is a generalized Lagrange space which is not reducible to a Riemann space, or to a Finsler space, or to a Lagrange space.
Notice that such a result is strictly related to the fact that the deformed metric tensor of DSR is diagonal.
If an external electromagnetic field ![]() is present in the Minkowski space
is present in the Minkowski space , in
, in 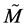 the deformed electromagnetic field is given by
the deformed electromagnetic field is given by . Such a field is a d-tensor and is called the electromagnetic tensor of the generalized Lagrange space. Then, the nonlinear connection
. Such a field is a d-tensor and is called the electromagnetic tensor of the generalized Lagrange space. Then, the nonlinear connection 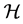 is given by
is given by
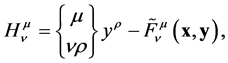 (34)
(34)
where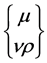 , the Christoffel symbols of the Minkowski metric
, the Christoffel symbols of the Minkowski metric![]() , are zero, so that
, are zero, so that
 (35)
(35)
namely, the connection coincides with the deformed field.
The adapted basis of the distribution  reads therefore
reads therefore
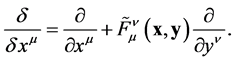 (36)
(36)
The local covector field of the dual basis (cfr. Equation (18)) is given by
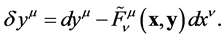 (37)
(37)
3.4. Canonical Metric Connection of 
The derivation operators applied to the deformed metric tensor of the space ![]() yield
yield
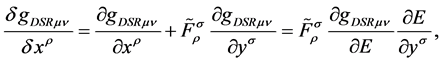 (38)
(38)
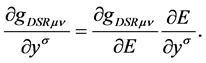 (39)
(39)
Then, the coefficients of the canonical metric connection  in
in 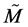 (see Equation (23 )) are given by
(see Equation (23 )) are given by
 (40)
(40)
The vanishing of the electromagnetic field tensor, 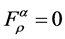 , implies
, implies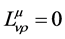 .
.
One can define the deflection tensors associated to the metric connection 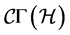 as follows (cfr. Equation (30)):
as follows (cfr. Equation (30)):
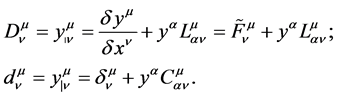 (41)
(41)
The covariant components of these tensors read
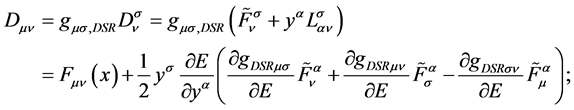
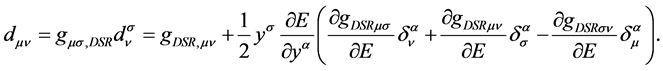 (42)
(42)
It is important to stress explicitly that, on the basis of the results of 3.2.1, the deformed Minkowski space 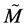 does possess curvature and torsion, namely it is endowed with a very rich geometrical structure. This permits to understand the variety of new physical phenomena that occur in it (as compared to the standard Minkowski space) [3] [4] . Notice that this result follows by the fact that, in deforming the metric of the space-time, we assumed the energy as the physical (non-metric) observable on which letting the metric coefficients depend. This is crucial in stating the generalized Lagrangian structure of
does possess curvature and torsion, namely it is endowed with a very rich geometrical structure. This permits to understand the variety of new physical phenomena that occur in it (as compared to the standard Minkowski space) [3] [4] . Notice that this result follows by the fact that, in deforming the metric of the space-time, we assumed the energy as the physical (non-metric) observable on which letting the metric coefficients depend. This is crucial in stating the generalized Lagrangian structure of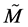 , as shown above.
, as shown above.
Following ref. [7] , let us show how the formalism of the generalized Lagrange space allows one to recover some results on the phenomenological energy-dependent metrics discussed in Section 2.
Consider the following metric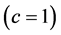 :
:
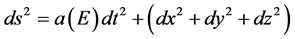 (43)
(43)
where 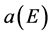 is an arbitrary function of the energy and spatial isotropy
is an arbitrary function of the energy and spatial isotropy 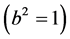 has been assumed. In absence of an external electromagnetic field
has been assumed. In absence of an external electromagnetic field , the non-vanishing components
, the non-vanishing components 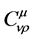 of the canonical metric connection
of the canonical metric connection 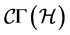 (see Equation (40)) are
(see Equation (40)) are
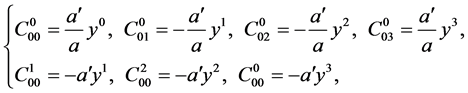 (44)
(44)
where the prime denotes derivative with respect to 
According to the formalism of generalized Lagrange spaces, we can write the Einstein equations in vacuum corresponding to the metrical connection of the deformed Minkowski space (see Equations (31)). It is easy to see that the independent equations are given by
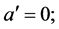 (45)
(45)
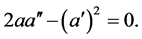 (46)
(46)
The first equation has the solution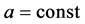 , namely we get the Minkowski metric. Equation (46) has the solution
, namely we get the Minkowski metric. Equation (46) has the solution
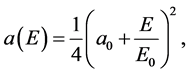 (47)
(47)
where 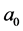 and
and 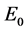 are two integration constants.
are two integration constants.
This solution represents the time coefficient of an over-Minkowskian metric. For 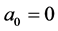 it coincides with (the time coefficient of) the phenomenological metric of the strong interaction, Equation (7). On the other hand, by choosing
it coincides with (the time coefficient of) the phenomenological metric of the strong interaction, Equation (7). On the other hand, by choosing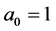 , one gets the time coefficient of the metric for gravitational interaction, Equation (7’).
, one gets the time coefficient of the metric for gravitational interaction, Equation (7’).
In other words, considering  as a generalized Lagrange space permits to recover (at least partially) the metrics of two interactions (strong and gravitational) derived on a phenomenological basis.
as a generalized Lagrange space permits to recover (at least partially) the metrics of two interactions (strong and gravitational) derived on a phenomenological basis.
It is also worth noticing that this result shows that a spacetime deformation (of over-Minkowskian type) exists even in absence of an external electromagnetic field (remember that Equations (45) and (46) have been derived by assuming![]() ).
).
3.5. Intrinsic Physical Structure of a Deformed Minkowski Space: Internal Gauge Fields
As we have seen, the deformed Minkowski space , considered as a generalized Lagrange space, is endowed with a rich geometrical structure. But the important point, to our purposes, is the presence of a physical richness, intrinsic to
, considered as a generalized Lagrange space, is endowed with a rich geometrical structure. But the important point, to our purposes, is the presence of a physical richness, intrinsic to . Indeed, let us introduce the following internal electromagnetic field tensors on
. Indeed, let us introduce the following internal electromagnetic field tensors on![]() , defined in terms of the deflection tensors:
, defined in terms of the deflection tensors:
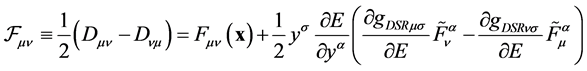 (48)
(48)
(horizontal electromagnetic internal tensor) and
 (49)
(49)
(vertical electromagnetic internal tensor).
The internal electromagnetic hand v-fields ![]() and
and ![]() satisfy the following generalized Maxwell equations
satisfy the following generalized Maxwell equations
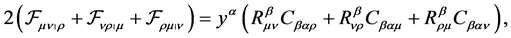
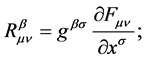 (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
Let us stress explicitly the different nature of the two internal electromagnetic fields. In fact, the horizontal field ![]() is strictly related to the presence of the external electromagnetic field
is strictly related to the presence of the external electromagnetic field![]() , and vanishes if
, and vanishes if![]() . On the contrary, the vertical field
. On the contrary, the vertical field ![]() has a geometrical origin, and depends only on the deformed metric tensor
has a geometrical origin, and depends only on the deformed metric tensor 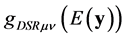 of
of ![]() and on
and on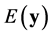 . Therefore, it is present also in space-time regions where no external electromagnetic field occurs. As we shall see, this fact has deep physical implications.
. Therefore, it is present also in space-time regions where no external electromagnetic field occurs. As we shall see, this fact has deep physical implications.
A few remarks are in order. First, the main results obtained for the (abelian) electromagnetic field can be probably generalized (with suitable changes) to non-abelian gauge fields. Second, the presence of the internal electromagnetic hand v-fields ![]() and
and![]() , intrinsic to the geometrical structure of
, intrinsic to the geometrical structure of 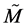 as a generalized Lagrange space, is the cornerstone to build up a dynamics (of merely geometrical origin) internal to the deformed Minkowski space.
as a generalized Lagrange space, is the cornerstone to build up a dynamics (of merely geometrical origin) internal to the deformed Minkowski space.
The important point worth emphasizing is that such an intrinsic dynamics springs from gauge fields. Indeed, the two internal fields ![]() and
and ![]() (in particular the latter one) do satisfy equations of the gauge type (cfr. Equations (51) and (52)). Then, we can conclude that the (energy-dependent) deformation of the metric of
(in particular the latter one) do satisfy equations of the gauge type (cfr. Equations (51) and (52)). Then, we can conclude that the (energy-dependent) deformation of the metric of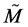 , which induces its geometrical structure as generalized Lagrange space, leads in turn to the appearance of (internal) gauge fields [6] .
, which induces its geometrical structure as generalized Lagrange space, leads in turn to the appearance of (internal) gauge fields [6] .
Such a fundamental result can be schematized as follows:
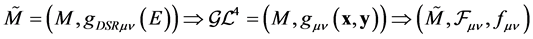 (53)
(53)
(with self-explanatory meaning of the notation).
4. Conclusions and Perspectives
In Deformed Special Relativity, two kinds of breakdown of Lorentz invariance occur. One is straightforward, and is due to the very dependence on energy of the metric coefficients. The second is more subtle, and is related to the mathematical structure of Generalized Lagrange space, which allows one to endow deformed Minkowski space-time with both curvature and torsion.
This is a basic result, not only from the theoretical, but also from the experimental side. Indeed, a number of experiments carried out in the last two decades have shown that a variety of new physical phenomena do occur in deformed space-time [4] [11] . In all the experiments performed so far, a remarkable space anisotropy has been observed. This deserves a thorough theoretical and experimental investigation.
References
- Mattingly, D. (2005) Modern Tests of Lorentz Invariance. Living Reviews in Relativity, 8, 5. http://www.livingreviews.org/lrr-2005-5
- Kostelecky, V.A. (1999, 2002, 2004) CPT and Lorentz Symmetry I, II, III. World Scientific, Singapore.
- Cardone, F. and Mignani, R. (2004) Energy and Geometry—An Introduction to Deformed Special Relativity. World Scientific, Singapore.
- Cardone, F. and Mignani, R. (2007) Deformed Spacetime—Geometrizing Interactions in Four and Five Dimensions. Springer, Heidelberg, Dordrecht. http://dx.doi.org/10.1007/978-1-4020-6283-4
- Cardone, F., Mignani, R. and Petrucci, A. (2011) The Principle of Solidarity: Geometrizing Interactions. In: Dvoeglazov, V.V., Ed., Einstein and Hilbert: Dark Matter, Nova Science, Commack, 19.
- Mignani, R., Cardone, F. and Petrucci, A. (2013) El. J. Theor. Phys., 29, 1.
- Miron, R., Jannussis, A. and Zet, G. (2004) In Tsagas, Gr., Ed., Proc. Conf. Applied Differential Geometry—Gen. Rel. and the Workshop on Global Analysis, Differential Geometry and Lie Algebra, 2001, Geometry Balkan Press, 101.
- Miron, R. and Anastasiei, M. (1994) The Geometry of Lagrange Spaces: Theory and Applications. Kluwer, Alphen aan den Rijn.
- Miron, R., Hrimiuc, D., Shimada, H. and Sabau, S.V. (2002) The Geometry of Hamilton and Lagrange Spaces. Kluwer, Alphen aan den Rijn.
- Steenrod, N. (1951) The Topology of Fibre Bundles. Princeton University Press, Princeton.
NOTES

1Let us recall that in 1955 the Italian mathematician Bruno Finzi stated his “Principle of Solidarity” (PS), that sounds “It’s (indeed) necessary to consider space-time TO BE SOLIDLY CONNECTED with the physical phenomena occurring in it, so that its features and its very nature do change with the features and the nature of those. In this way not only (as in classical and special-relativistic physics) space-time properties affect phenomena, but reciprocally phenomena do affect space-time properties. One thus recognizes in such an appealing “Principle of Solidarity” between phenomena and space-time that characteristic of mutual dependence between entities, which is peculiar to modern science.” Moreover, referring to a generic N-dimensional space: “It can, a priori, be pseudoeuclidean, Riemannian, non-Riemannian. But-he wonders-how is indeed the space-time where physical phenomena take place? Pseudoeuclidean, Riemannian, non-Riemannian, according to their nature, as requested by the principle of solidarity between space-time and phenomena occurring in it.”
Of course, Finzi’s main purpose was to apply such a principle to Einstein’s Theory of General Relativity, namely to the class of gravitational phenomena. However, its formulation is as general as possible, so to apply in principle to all the known physical interactions. Therefore, Finzi’s PS is at the very ground of any attempt at geometrizing physics, i.e. describing physical forces in terms of the geometrical structure of space-time.

2As is well known, all the present physically realizable detectors work via their electromagnetic interaction in the usual space-time M. So, 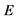 is the energy of the system measured in fully Minkowskian conditions.
is the energy of the system measured in fully Minkowskian conditions.
3At least for strong interaction; nothing can be said for the gravitational one.

4The analogy of this second kind of metric gauge with the standard, non-Abelian gauge theories is more evident in the framework of the five-dimensional space-time 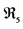 (with energy as extra dimension) embedding
(with energy as extra dimension) embedding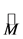 , on which Deformed Relativity in Five Dimensions (DR5) is based (see ). In
, on which Deformed Relativity in Five Dimensions (DR5) is based (see ). In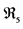 , in fact, energy is no longer a parametric variable, like in DSR, but plays the role of fifth (metric) coordinate. The invariance under such a metric gauge, not manifest in four dimensions, is instead recovered in the form of the isometries of the five-dimensional space-time-energy manifold
, in fact, energy is no longer a parametric variable, like in DSR, but plays the role of fifth (metric) coordinate. The invariance under such a metric gauge, not manifest in four dimensions, is instead recovered in the form of the isometries of the five-dimensional space-time-energy manifold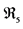 .
.

5Namely it must be![]() .
.
6Let us recall that a Finsler space is a couple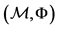 , where
, where 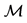 is be an N-dimensional differential manifold and
is be an N-dimensional differential manifold and 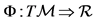 a function
a function 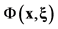 defined for
defined for 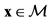 and
and 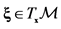 such that
such that 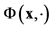 is a possibly non symmetric norm on
is a possibly non symmetric norm on .
.
Notice that every Riemann manifold 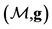 is also a Finsler space, the norm
is also a Finsler space, the norm 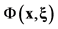 being the norm induced by the scalar product
being the norm induced by the scalar product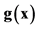 .
.
A finite-dimensional Banach space is another simple example of Finsler space, where .
.

7 plays the role of a curvature tensor of the nonlinear connection
plays the role of a curvature tensor of the nonlinear connection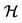 . The corresponding tensor of torsion is instead
. The corresponding tensor of torsion is instead
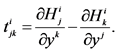

8Contrarily to ref. , we shall not consider the restrictive case of a classical (non-relativistic) expression of the energy, but assume a general dependence of E on the velocity (Equation (32)).

