Natural Science
Vol.5 No.6(2013), Article ID:32947,4 pages DOI:10.4236/ns.2013.56084
Neutrino speed can exceed the speed of light within the frame work of the generlized special relativity and savckas model
![]()
1Department of Physics, Sudan University of Science and Technology, Khartoum, Sudan; mahmoudhilo@gmail.com
2Department of physics, Qassim University, Qassim, KSA; *Corresponding Author: mhhlo@qu.edu.sa
3Department of Physics, Faculty of Education, International University of Africa, Khartoum, Sudan
Copyright © 2013 Mubarak Dirrar et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 31 January 2013; revised 2 March 2013; accepted 10 March 2013
Keywords: Generalized Special Relativity; Neutrino speed; OPERA; Savickas Model
ABSTRACT
The speed of Neutrino particles is shown to be greater than that of light as shown by the OPERA neutrino experiment at the underground Gran Sasso Laboratory. The result of this experiment can be explained within the framework of the Generalized Special Relativity and Savickas model.
1. INTRODUCTION
One of the most important postulates in physics is utilized by Einstein at the beginning of the 20th century (1905), within the theory of special relativity, which states that the speed of light (300,000,000 m/s) in vacuum is constant and independent of the motion of the source or observer, and it represents the upper limit of the speed of any particle in the nature. Or we can say nothing can travel faster than light. Such amazing theory or postulate cannot be change unless we get something that can travel faster than light, that’s the neutrino particles.
Neutrino particle is first proposed by Pauli in 1930, to conserve energy in the beta decay process. Fermi later named this particle the neutrino. The neutrino has no electric charge, spin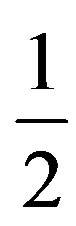 , interacts weakly with matter, and has very small mass [1].
, interacts weakly with matter, and has very small mass [1].
It also plays an important role in cosmology. It contributes to the so-called dark matter, which is utilized to explain the critical mass problem [2] and solve some cosmological problem in the early universe [3,4]. It is also utilized to detect supernova activities. Recently the neutrino mass is found to be strongly dependent on the environment or particle associated with it, for the instance, the electron neutrino has a mass different from the tau neutrino and muon neutrino. This mass variation is explained recently by utilizing the Generalized Special Relativity (GSR) theory [5], all these on one hand.
On the other hand, an Italian experiment has unveiled evidence that fundamental particles known as neutrinos can travel faster than light. Other researchers are cautious about the result, but if it stands further scrutiny, the finding would overturn the most fundamental rule of modern physics—that nothing travels faster than 299,792,458 meters per second. The experiment is called OPERA (Oscillation Project with Emulsion-Tracking Apparatus), and lies 1400 meters underground in the Gran Sasso National Laboratory in Italy. It is designed to study a beam of neutrinos coming from CERN, Europe’s premier highenergy physics laboratory located 730 kilometers away near Geneva, Switzerland. Neutrinos are fundamental particles that are electrically neutral, rarely interact with other matter, and have a vanishingly small mass. But they are all around us—the Sun produces so many neutrinos as a by-product of nuclear reactions that many billions pass through your eye every second. The 1800- tonne OPERA detector is a complex array of electronics and photographic emulsion plates, but the new result is simple—the neutrinos are arriving 60 nanoseconds faster than the speed of light allows. “We are shocked,” says Antonio Ereditato, a physicist at the University of Bern in Switzerland and OPERA’s spokesman [6,7].
The measurements taken by OPERA in the years 2009- 2011 shows that the neutrino speed v exceeds that of light, where
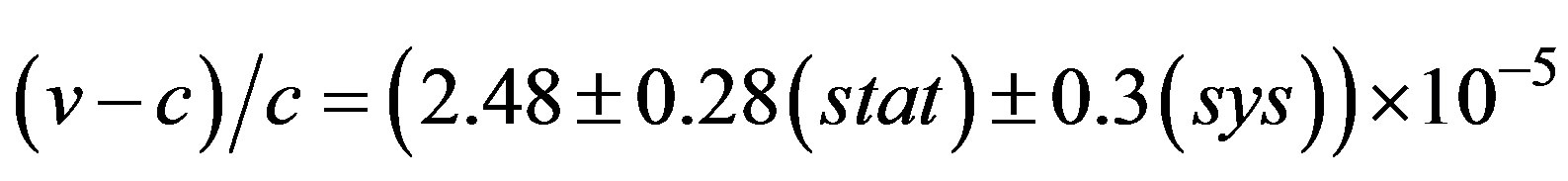
This high speed v which is larger than the speed of light c, is very difficult to be explained within the frame work of special relativity (SR) promoted by Dirac [8], but, the Generalized Special Relativity (GSR) and Savickas can explain why the neutrino speed v exceeds the speed of light c. When Euclidean coordinate lengths are replaced by the metric lengths of a curved geometry within Newton’s second law of motion, the metric form of the second law can be shown to be identical to the geodesic equation of motion of general relativity. The metric coefficients are contained in the metric lengths and satisfy the field equations of general relativity. Because metric lengths are the physically measured lengths, their use makes it possible to understand general relativity directly in terms of physical quantities such as energy and momentum within a curved space-time. The metric form of the second law contains gravitational effects in exactly the same manner as occurs in relativity. Its mathematical derivation uses vectors rather than tensors, and nongravitational forces can occur in this modified second law without a tensor form. Because quantum mechanics is based on Newtonian concepts of energy and momentum, it is shown that when metric lengths replace coordinate lengths in Dirac’s wave equation, it has a covariant form under a metric transformation of the physically measured distances themselves, rather than a coordinate transformation. Metric transformations are also used to describe the Dirac equation for the gravitational central field in a Schwarzschild metric [8].
This work utilizes GSR and Savickas models to explain why the neutrino speed v exceeds the speed of light c, as shown in Section 4. Section 2 is concerned with SR, while Section 3 is devoted for exhibiting the GSR and Savickas model. In Section 5, GR with the new version of GSR and Savickas model is presented.
2. SPECIAL RELATIVITY (SR)
According to Einstein’s special relativity (SR) the time (t), length (L), the mass (m), and the energy (E) are velocity dependent, and are given by:
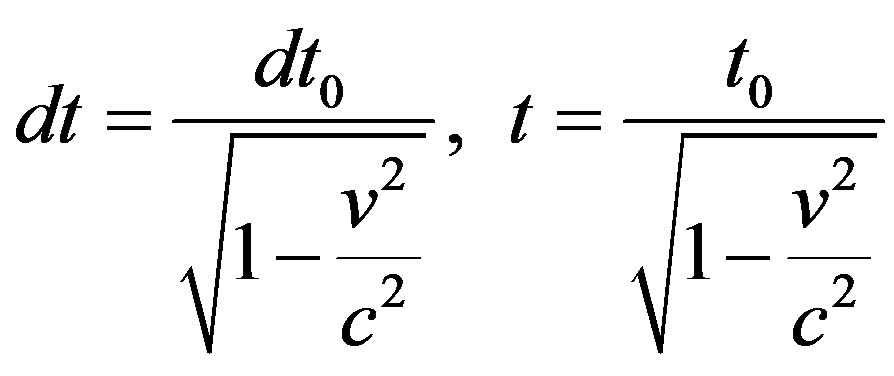 (1)
(1)
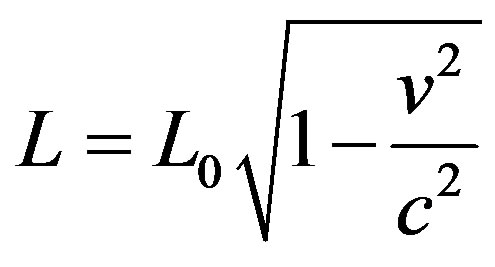 (2)
(2)
And
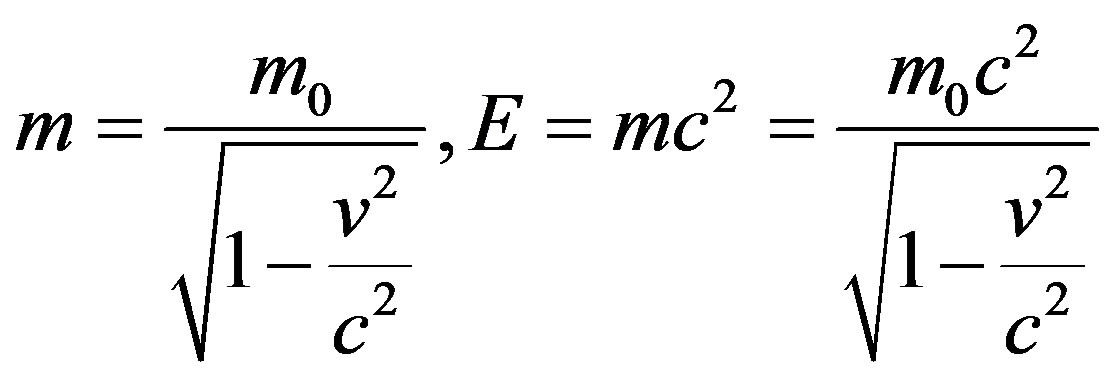 (3)
(3)
The SR theoretical foundation and frame work is based on two postulates:
1) The speed of light in vacuum c is constant and is independent of the motion of the source or observer;
2) The laws of physics take the same form in all inertial frame of references. So according to Eqs.1-3 the particle speed cannot exceed the speed of light c, since for C, then t, L, m, and E become imaginary.
3. GENRALIZED SPECIAL RELATIVITY AND SAVICKAS MODEL
Generalized special relativity theory (GSR) is a theory modifies SR to incorporate the effect of the field’s potentials in time, length, mass, and energy [9]. According to this new version the Eqs.1 and 3 are derived to be as:
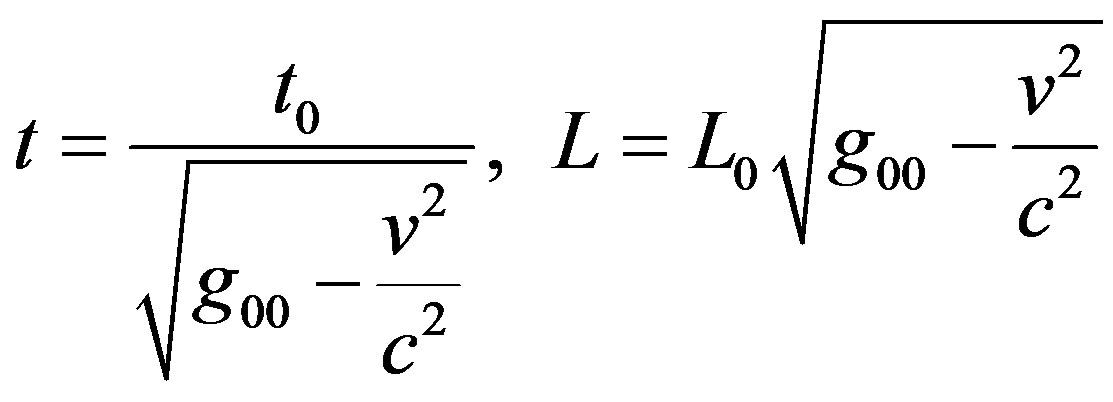 (4)
(4)
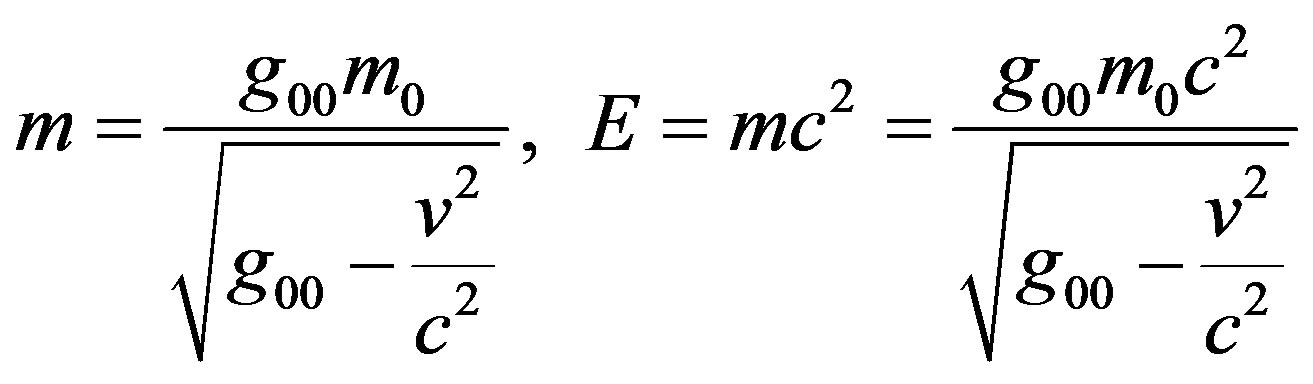 (5)
(5)
In Savickas model the 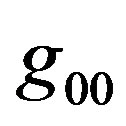 in the numerator is absent, thus:
in the numerator is absent, thus:
 (6)
(6)
where , and
, and 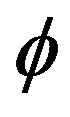 being the potential per unit mass.
being the potential per unit mass.
This model is utilized to explain the mass defect inside the nucleus, besides explaining the difference in the mass between electron neutrino, muon neutrino, and tau neutrino [10].
4. DISCUSSION
According to the SR the mass and energy are given by Eq.3. If the speed of any particle exceed the speed of light c, i.e.
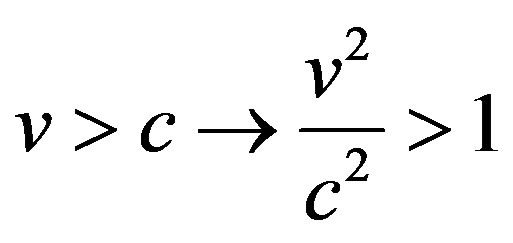 (7)
(7)
The mass and energy become imaginary quantities, which is not physically acceptable, as far as the physical quantities in our real world are real. This means that if alternative expressions for mass and energy in which the speed of any particle v can exceed the speed of light c without making m and E imaginary is found, the speed of light in vacuum is no longer represents the upper bound for the speed of particles in nature. This means that in such model, it is physically acceptable to have particles with speeds v exceeding the speed of light c. fortunately, the expression of m and E in GSR and Savickas model can explain why the neutrino speed v exceeds the speed of light c. The expressions of the mass m and energy E in GSR are given by Eq.5.
Where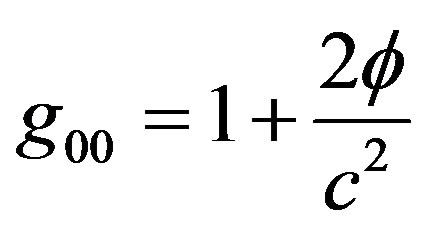 , and
, and 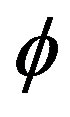 being the potential per unit mass.
being the potential per unit mass.
In the neutrino experiment, at CERN, the neutrino is accelerated by applying a certain field to the proton particle which consists of neutron, positron, and neutrino. In this process the neutrino is accelerated. Thus the kinetic energy of it can not exceed the accelerating potential, i.e.
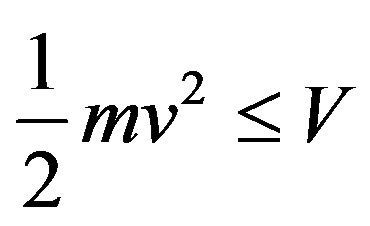 .
.
Thus
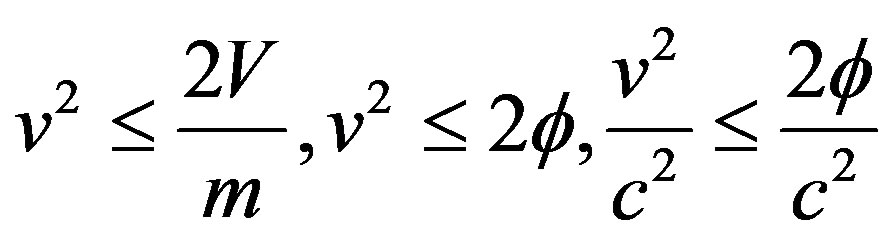 (8)
(8)
where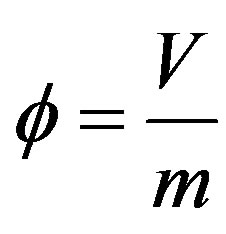 , Thus
, Thus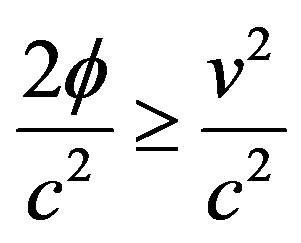 .
.
Hence
 . (9)
. (9)
Therefore according to Eq.5, E and m are no longer imaginary quantities, thus it is possible, within the frame work of GSR, to have particles with speeds exceeding the speed of light c, without violating the fact that physical quantities are real. This requires either the potential energy V to exceed the particle kinetic energy, or to have strong vacuum energy Vc, such that:
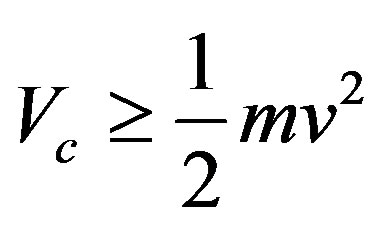
where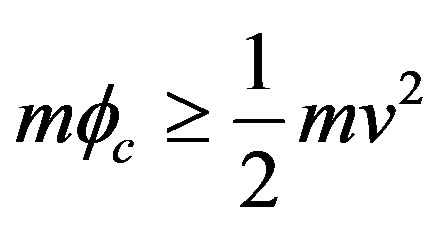 .
.
And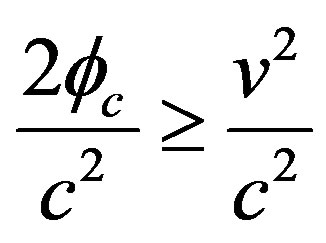 .
.
It is thus quite easy to explain the fact that the neutrino speed v can exceed the speed of light c, within the frame work of GSR and Savickas models.
5. NEW POSTULATES OF SR WITHIN THE FRAME WORK OF GSR AND SAVICKAS MODELS
According to the GSR and Savickas model, the postulates of relativity can be rested as follows:
1) All frames of reference are equivalent;
2) The speed of light in vacuum is constant and independent of the motion of the source or observer. The speed of light in the new version of SR does not represent the upper limit to the speed of particles, but a third postulate can limit here the speed of any particle according to Eqs.8 and 9 which requires:
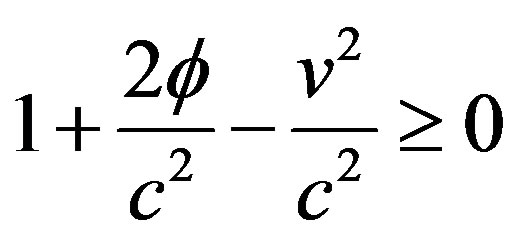
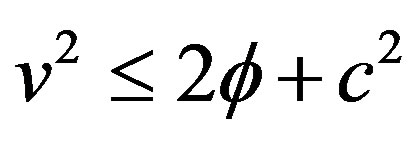 .
.
Thus the maximum speed:
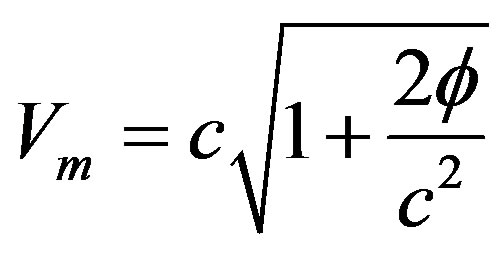 .
.
Can exceed the speed of light by a factor
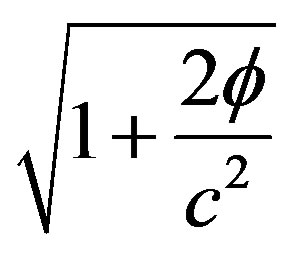 .
.
6. CONCLUSION
The GSR and Savickas models can explain the experiment in which the neutrino is observed to have speed greater than that of light in vacuum. This does not violate the SR postulate which states that the speed of light in vacuum is constant, and is independent of the motion of the source or observer. However, the speed of light in vacuum is no longer representing the upper limit of speed of particles, in GSR and Savickas models, as in SR.
REFERENCES
- Serway, R.A. (2004) Physics for scientists and engineers. In: Jewett, J.W., 6th Edition, California State Polytechnic University, Pomona.
- Xu, C., Uis, G.F.R.E., Xu, X.J. and El Tahir, A. (1992) The generalized field equation. South African Journal of Physics, 15, 5.7.
- Narlikar, J.V. (1993) Introduction to cosmology. 2nd Edition, Cambridge University Press, Cambridge.
- Suen, W.M. and Anderson, P.R. (1986) Physical Review D, 35, 2940.
- Hilo, M.H.M., et al. (2011) Using of the generalized special relativity (GSR) in estimating the neutrino masses to explain the conversion of electron neutrinos. NS, 3, 334- 338. doi:10.4236/ns.2011.32020
- Adam, T., et al. (2012) Measurement of the neutrino velocity with the OPERA detector in the CNGS beam-OPERA Collaboration (Adam, T. et al.). JHEP, 1210, 93.
- Acquafredda, R., et al. (2009) The OPERA experiment in the CERN to Gran Sasso neutrino beam, JINST, 4, 4018. doi:10.1088/1748-0221/4/04/P04018
- Savickas, D. (2002) Relation between Newtonian mechanics, general relativity and quantum mechanics. Journal of Physics, 70, 798-807. doi:10.1119/1.1479740
- Hilo, M.H.M., et al. (2011) Using of the generalized special relativity in estimating the proton (nucleon) mass to explain the mass defect. NS, 3, 141-144. doi:10.4236/ns.2011.32020
- Hilo, M.H.M., et al. (2012) Generalized general and special relativity in the presence of the gravitation, related to the space-time curvature. NS, 4, 336-339. doi:10.4236/ns.2012.45046

