Natural Science
Vol.5 No.1(2013), Article ID:26553,7 pages DOI:10.4236/ns.2013.51003
A mathematical perspective on the determination of coastal peopling nuclei
![]()
Département de Mathématiques et de Statistique, Université de Moncton, Moncton, Canada; *Corresponding Author: claude.gauthier@umoncton.ca
Received 24 October 2012; revised 27 November 2012; accepted 8 December 2012
Keywords: Mathematical Modeling; Coastal Peopling; Sea Level Rise; Coastal Archaeology; Mediterranean Peopling Nuclei; New Brunswick Acadians
ABSTRACT
Two versions of a mathematical model are proposed for the process underlying the choice of settlement sites of past, present and future populations along the world coastline. The model is primarily based on the geometry of coastline at the scale of the map representing the region under study. It can be used to determine sites of human occupation for archaeological interest, as well as to plan future movements of present coastal populations due to the current sea level rise. Two examples related to history are presented: the first applies to the coastal peopling of the Mediterranean region, and the second to the settlement of Acadians in North-East of the Canadian province of New Brunswick in the second half of the 18th century.
1. INTRODUCTION
Beyond the often narrative history of nations with its colors and heroes, it is possible to consider the history of mankind as an objective discipline to which mathematical methods can be applied. When examining the distribution of the world population, the universality of attraction of the coastal area on humans is immediately apparent. More than 60% of the population is concentrated on a strip of one million kilometer long and about sixty kilometer from the shore wide. Two thirds of all cities over 2.5 million inhabitants are located along estuaries [1]. Understanding the peopling of coastal area is important for both historical studies and future needs. The current sea level rise indeed makes it important to envisage the relocation of certain coastal populations, preferably along the future shoreline. What sites must be privileged to settle these populations? The objective of this paper is to exemplify the use of mathematics into history through a model that explains the siting of human settlement nuclei along the contemporary world coastline.
2. SITE AND INDUCED EFFECTS
The originality of coastal communities lies in the fact that the natural and social forces which govern their hatching and evolution are determined by the discontinuity between land and sea. The coastal area is by nature open to exchanges. It implies the idea of meeting and outside influence. Even if the time base can differ from one culture to another, archaeology and history show how humanity has gradually taken possession of the littoral zone. The observed variation in coastal settings shows that a number of factors are needed to explain this peopling process through space and time. The diversity of situations suggests a tangle of causes and forces.
Factors influencing coastal communities fall into two categories [2]: internal, depending only on the physical characteristics of the coastal region considered, and external, which depend on events occurring outside this region. Internal factors are mainly matter of a large geographic scale analysis, while external factors are involved when the scope of analysis reaches the middle or small scales. A deep understanding of the peopling process of a coast must take into account all internal and external factors, as well as their combined effects. The construction of a model based on dominant factors underlying the peopling of a coast area will allow a better understanding of how this process works. As for any complex phenomenon, this model requires simplifying assumptions. The main factors must first be identified.
Let us consider the internal factors. The installation of a community and its possible extension depends primarily on the physical configuration of the shore, the space available and opportunities for movement. Traditionally, humans have sought concavities which most of the time offer better shelters than convexities. The first internal factor is thus the coastal geometry assessed in terms of rate of change of the spatial continuity of the longitudinal and transverse profiles. The first line determines the degree of indentation and the second the width of the coastal zone. The elevation of this area adds a variation to the transverse continuity. The state of longitudinal connections and their links with the transverse axes of movement is another important factor of the dynamics of a coastal region. In general, a narrow shore is less conducive to human settlement, because people are then directly exposed to any violence coming from the sea without possibility of withdrawal. On both sides of the coastline, the morphological and hydrological characteristics determine the degree of opening of the shore toward the sea or the inland. On the sea side of the coast, the islands close to continents or grouped into archipelago were occupied very early in the history of mankind. The exploitation of fisheries resources and the hunting of marine mammals also provide livelihoods and properties to exchange which contributes to the installation and maintenance of riparian communities. On the land side of the coast, more opening means a greater integration of the shore to human activities. The dynamics of a coastal region depends on its potential spatial depth, and therefore on its degree of connection to the network of transverse communication routes. Hence, the existence of a notch in the cliff or of a plain formed by a river facilitates the opening toward the hinterland. Another point giving an advantage to the littoral zone is its climate which is generally more moderate than in the hinterland. However, under certain climatic conditions (polar regions) and morphological situations (bordering desert or too small island area), the coast as well as the inland present serious obstacles to human settlement. All these internal factors are cumulative and form the site effect.
Regarding the external factors, a coastal development is partly attributable to a set of elements that maintains the system dynamics and has little to do with the physical characteristics of the site. Indeed, when the activity reaches a critical level, the peopling is accompanied by a bundle of trade relations whose importance will depend on the permeability of the coast seen as a membrane. These external factors origin from more or less distant inland and overseas regions. For example, up to a recent period, the coastal shipping has maintained an important activity in many ports of the world coastline. Fishing activities have also led to the creation of seasonal or permanent basis on many shores. The degree of isolation of a coastal region, or its state of peripheries with regard to economic centers, will determine its ability to exchange with inland regions. As internal factors, external factors are cumulative and constitute the induced effect. Note that the site and induced effects will not be applied to determine the maritime activities strictly speaking but rather the possibilities of relations between the communities of the inland and coastal zone.
3. AN ALGORITHMIC MATHEMATICAL MODEL
From the main internal and external factors identified, a careful analysis of the map of any given coastal region would yield good indications of the best places where to settle population nuclei along the coastline. To formalize this approach and to make it applicable to any coastline map, an algorithm was constructed and programmed for its computerized implementation. For simplicity, the model will first be limited to the internal factors related to the two-dimensional geometry of the coastline for a given geographic scale. We shall then add the internal factors associated with the degree of opening of the coastline toward the open sea, and to the presence along the coastline of rivers whose importance matches the geographic scale. The algorithm will involve parameters depending on the geographic scale and on the degree of indentation of the coastline. The values of these parameters are determined by comparing the model predictions with known distributions of present and ancient populations along some coasts.
Our method requires to first discretize the coastline map by overlapping it with a uniform rectangular grid with cell size proportional to the map geographic scale. Cell size should be such that the number of pixels in each is approximately equal to the total number of pixels forming the map divided by 20,000. The area of a typical cell being so fixed, its sizes are then determined to be as close as possible to that of a square. Cells intersecting the coastline are called coastal. We then give a fixed numerical value, e.g. 10, to each coastal cell and the value 0 to all other cells. Finally, each cell of the gridded map is assigned the sum of the values of the nine cells making up the 3 by 3 mobile grid having this cell as center [3]. If the geographic scale is relatively large and the shoreline is sufficiently fine, that is if it has a width of one pixel, then a given cell will be said active if its value reaches a certain threshold, such as 50 or 60 when each coastal cell value is 10. If the coastline has a width of two or more pixels and cannot be refined without creating discontinuities, this threshold must be increased to achieve similar results. If active cells are colored in grey, the outcome of this exercise is a gridded map with more grey cells in the regions where the coast is jagged. Note that grey cells may be located over areas consisting entirely of water. The goal here is not to determine where the peopling will take place, but rather to identify the regions most likely to have the largest exchange activity between people: this activity will promote peopling of the land part of the area put forward.
If the geographic scale is of medium or small sizes, then the preceding rules determining when a cell becomes active must be amended to reflect the influence of small size morphological structures which are invisible on large scale maps, such as reefs and barrier beaches. To reduce the importance of these structures that often cause problems for inhabitants of the coast, and sometimes make it uninhabitable, we assign to the corresponding coastal cells weighs less than regular coastal cells. At these medium and small scales, it may also appear morphological structures favorable to human settlement. These structures are related to the degree of opening of the coastal zone, such as the mouth of a river. The importance of such streams is taken into account by assigning to the cells of the coastline located near the mouth of a river weights higher than the one of regular coastal cells. These weights will here be determined by the catchment area of the river. Also, we shall assume that the weight given to a cell in the vicinity of an estuary increases as its location approaches the mouth itself.
It is possible to build models where the intensity of occupation of a coast varies with time. A basic evolutionary scenario of this kind is obtained by varying the value of the threshold for a cell to become active. The occupation process could then start in cells having eight neighbors cut by the coastline, i.e. cells whose threshold is 90, when each coastal cell value equals 10. If a coastal community develops a sufficiently strong self-confidence, it will often decide to reduce the reassuring proximity of the neighboring region along the coastline. In our model, this corresponds to a reduction of the threshold value for a cell to become active. If the value of each coastal cell equals 10, this reduction will bring the threshold to a multiple of 10 between 80 and 40. The lower limit of 40 is introduced because a threshold lower than this value would imply that all coastal cells would meet the value to be active and consequently, that no information could be deduced from this kind of analysis. If we consider as the first step of occupation the appearance of first active cells, then the evolution can go through at most six steps, one for each of the multiples of 10 between 90 and 40.
We shall now apply the method just described to two regions of the world where the peopling was sufficiently delimited in time to yield interesting results despite the small number of factors taken into consideration.
4. FIRST EXAMPLE: THE MEDITERRANEAN REGION
It is in the eastern basin of the Mediterranean Sea that people along the coastline began maritime operations, occupying the shores, establishing trading posts and settlements, creating a network of more and more dense relations between islands and the coastline. The peopling was then carried out from multiple centers, while preserving the unity in the development of a maritime community based on an exchange network. After the Cretans, the Achaeans created several colonies throughout the Aegean Sea. The Phoenicians then took over before the arrival of Greeks. Pushed to emigration by lack of land and poor soil, and also by commercial ambitions, they created between the 8th and 6th centuries B.C. many colonies on the eastern coast of the Mediterranean Sea, around the Black Sea and also along the western coast of the Mediterranean Sea. To these Greeks, there was no geographic barrier between the inhabitants of the coastline and those of the inland. There was just a social barrier due to different lifestyles. These Greeks have created the largest coastal community of the time, which also proved to be the most stable of the historic period.
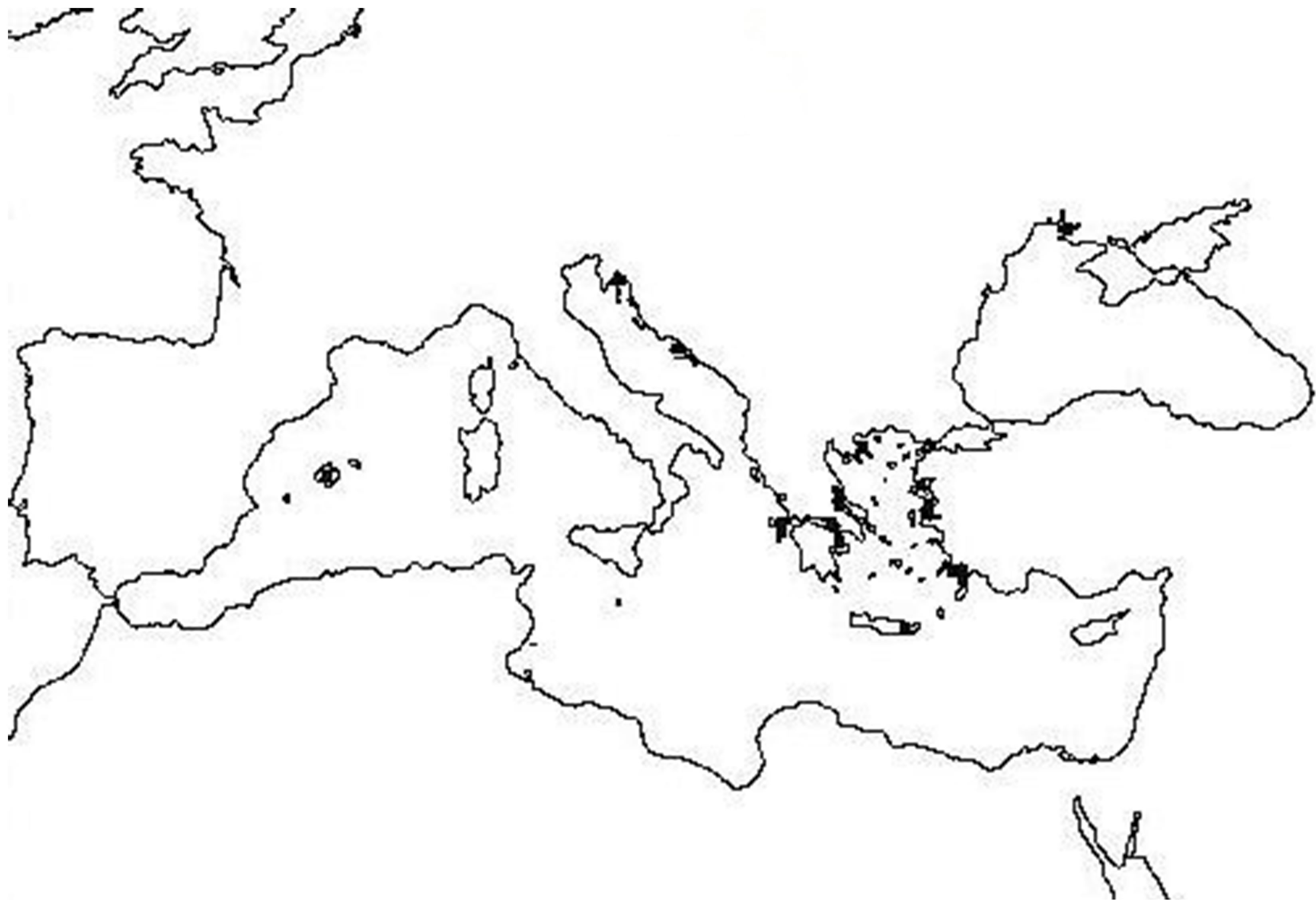
To describe how Greeks settle around the Mediterranean Sea, let us implement our model reduced to the single internal factor of the coastline geometry. The scale of the map to which our model will be applied is about 1/2,000,000. The superimposed grid has 168 cells horizontally and 114 vertically. With a coastal cell value of 10 and a threshold of 60, the model yields the map of Figure 1(b). In the eastern part of the Mediterranean basin grey cells cover the coasts of: (1) the Greek Peninsula and (2) the Aegean Sea, as well as (3) Ionia and its extension toward (4) the Bosphorus. Also, we find grey cells along the coast of (5) Crimea, (6) the North-East shore of the Azov Sea, (7) Cyprus, (8) South of Italy, (9) Sicily and (10) Dalmatia. The sites of all Greeks’ major population centers of this era appear clearly. The only area of the eastern coast of the Mediterranean Sea highlighted by this analysis that was not colonized by Greeks is Dalmatia. Putting aside this exception, there is thus a strong correlation between the predictions of our model and the actual peopling of ancient Greeks.
Other coastal areas identified by this model are found primarily in the western part of the Mediterranean Sea, which at that time was controlled by (11) Carthage. Also here the coastal regions determined by the model correspond to the nuclei of the Carthaginian civilization. Our results corroborate and improve those of a previous work that was manually realized, and which served as starting point of the present study [4]. New sites outside the Mediterranean coast are also found. For example, on the Atlantic coast of Europe we find: (12) the Normandy coast in France as well as the estuaries of (13) the Gironde, (14) Severn, (15) Thames and (16) Tagus rivers. Finally, at the northern end of the Red Sea are found the regions of (17) Suez and (18) Aqaba.
According to the evolutionary scenario described at the end of the preceding section, the state of evolution shown in Figure 1(b) corresponds to the fourth step of occupation of the Mediterranean region. The application of the above algorithm with a threshold of 90 leads to the first step of occupation shown in Figure 1(a). Grey cells
 (a)
(a)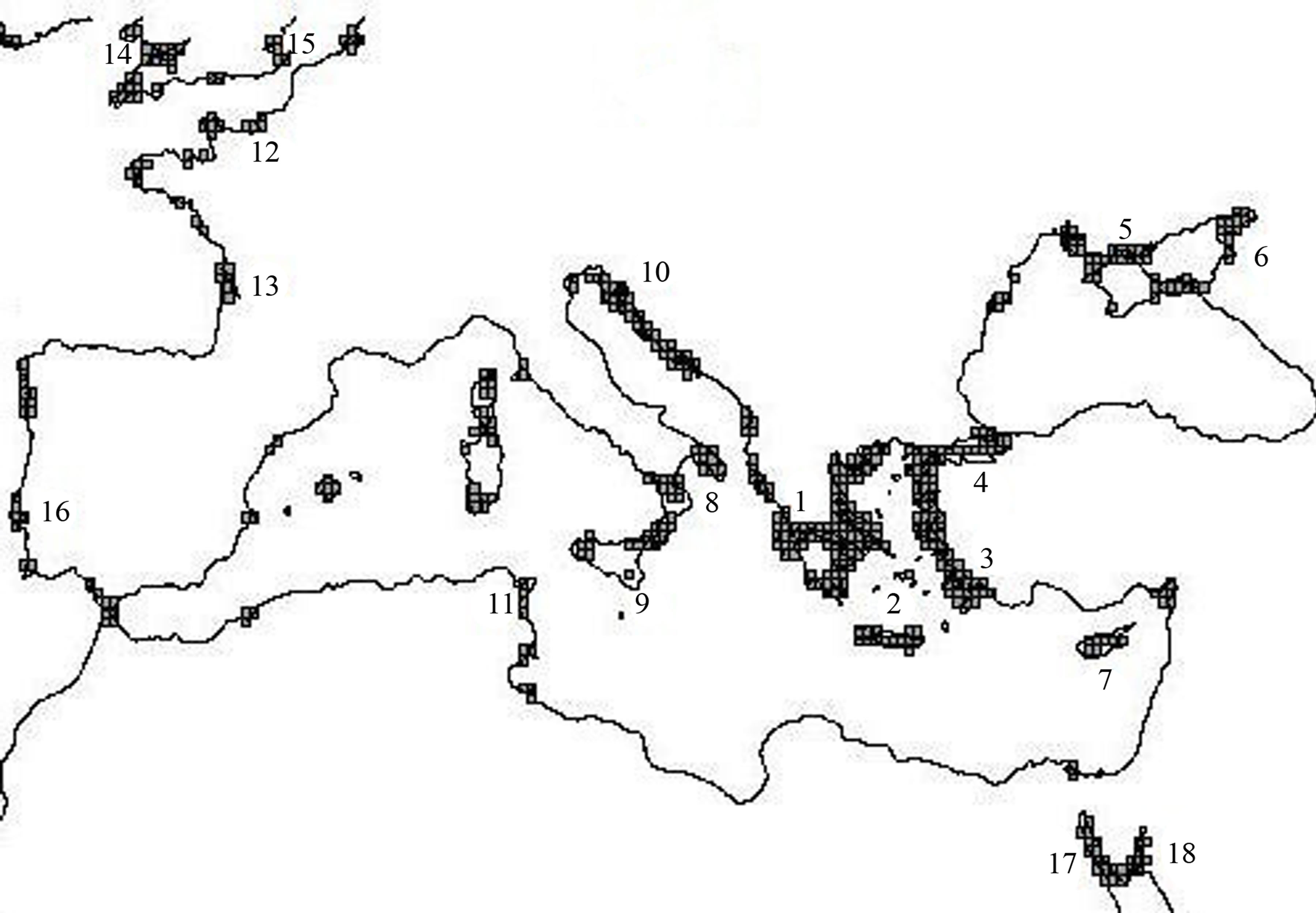 (b)
(b)
Figure 1. Two pictures showing the evolution of human occupation of the Mediterranean coastal region. Grey cells correspond to places where people were most likely to settle. Here the value of each coastal cell equals 10 and the thresholds for a cell to become active are 90 (map (a)), and 60 (map (b)). The correspondence between numbers and place names on map (b) is given in the text.
of map (a) are very sparse, with one cell over Majorca, one over the North-West shore of the Black Sea and about fifteen around the Aegean Sea.
5. SECOND EXAMPLE: NORTHEASTERN NEW BRUNSWICK
For any given coastal region, the arrival by sea of alien populations must be regarded as an external factor originating from overseas. Among receiving coasts, we distinguish those of new countries for which a simple peopling model has a good chance to drive realistic forecasts. In the second part of 18th century, the North-East coast of the Canadian province of New Brunswick was still so sparsely populated that it can be considered as a new country shore. This coastal area has served as refuge to a part of people who fled the ethnic cleansing practiced by British in Acadia between 1755 and 1763, during the Seven Years’ War between Great Britain and France [5]. The area of interest here includes a region called Acadian Peninsula, because it still inhabited by descendants of these refugees. This area is bounded on the West by the little town of Dalhousie, on the North by the Chaleur Bay, on the East by the St. Lawrence Gulf and on the South by the village of Neguac.
The geographic scale of the map we have used is about 1/750,000 and the superimposed grid has 143 cells horizontally and 127 vertically. At this scale, the coastline is relatively smooth on the North, but very rugged with barrier beaches on the East. The model we have applied to the Mediterranean region would here greatly overestimate the settlement potential along the East coast. To adapt our model to such a map, we give the weight 0 instead of 10 to the problematic coastal cells and the weight 8 to the regular coastal cells along this section of coast. Similarly, our model for the Mediterranean region would underestimate the benefit of access roads to the inland that are the estuaries of important rivers at this scale. To take account of this benefit, we have given to the coastal cells located in the area where the four largest rivers joint the coast a weight above that of regular coastal cells. Two of these rivers joint the coast in the vicinity of Bathurst: they are called Nepisiguit and Tetagouche, with watersheds areas of about 2500 km2 and 550 km2 respectively. The two other largest rivers are Big Tracadie and Tabusintac with mouths near the communities of Tracadie-Sheila and Tabusintac, and watersheds of about 650 km2 and 825 km2, respectively.
The weights assigned to the cells surrounding the mouth rivers are the area (in km2) of their catchment basins. For each river one third of this number is distributed among the cells of the coastline according to the function
 where x denotes the distance in pixels from the mouth of the watercourse, p is the weight to be distributed and r is the length of the section of coast where 50% of this weight is distributed. This length is here settled on
where x denotes the distance in pixels from the mouth of the watercourse, p is the weight to be distributed and r is the length of the section of coast where 50% of this weight is distributed. This length is here settled on 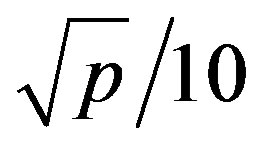 and is measured from the mouth of the river. The remaining two thirds of the weight to be distributed are spread out along the course of the river near its mouth according to the same function, where p is modified accordingly and the length r is again measured from the mouth of the river. With these modifications and a threshold of 50, our model leads to Figure 2(a), where the height of the column over a cell is equal to its weight. To facilitate the localization of found places, we have situated them on the two-dimensional projection of Figure 2(a) given by Figure 2(b). Starting at the NorthWest extremity of the map, we find the sites where have grown the small town of (1) Dalhousie, and the villages of: (2) Charlo, (3) Benjamin River (4) Black Point, (5) Nash Creek, (6) Belledune and (7) Pointe-Verte. At the bottom of the bay of Nepisiguit is located a smaller bay around which lies the town of (8) Bathurst. By heading eastward and then southward, we find the sites of: (9) Janeville, (10) Clifton, (11) Stonehaven, (12) Pokeshaw, (13) Grande-Anse, (14) Maisonnette/Anse-Bleue, (15) Bertrand, (16) Pointe-Canot, (17) Petit-Shippagan, (18) Miscou Centre, (19) Lamèque, (20) Shippagan, (21) Saint-Simon, (22) Inkerman, (23) Pokemouche/Maltampec, (24) Tracadie-Sheila, (25) Leech/Pont-Lafrance, (26) Price Settlement/Tabusintac and (27) Neguac.
and is measured from the mouth of the river. The remaining two thirds of the weight to be distributed are spread out along the course of the river near its mouth according to the same function, where p is modified accordingly and the length r is again measured from the mouth of the river. With these modifications and a threshold of 50, our model leads to Figure 2(a), where the height of the column over a cell is equal to its weight. To facilitate the localization of found places, we have situated them on the two-dimensional projection of Figure 2(a) given by Figure 2(b). Starting at the NorthWest extremity of the map, we find the sites where have grown the small town of (1) Dalhousie, and the villages of: (2) Charlo, (3) Benjamin River (4) Black Point, (5) Nash Creek, (6) Belledune and (7) Pointe-Verte. At the bottom of the bay of Nepisiguit is located a smaller bay around which lies the town of (8) Bathurst. By heading eastward and then southward, we find the sites of: (9) Janeville, (10) Clifton, (11) Stonehaven, (12) Pokeshaw, (13) Grande-Anse, (14) Maisonnette/Anse-Bleue, (15) Bertrand, (16) Pointe-Canot, (17) Petit-Shippagan, (18) Miscou Centre, (19) Lamèque, (20) Shippagan, (21) Saint-Simon, (22) Inkerman, (23) Pokemouche/Maltampec, (24) Tracadie-Sheila, (25) Leech/Pont-Lafrance, (26) Price Settlement/Tabusintac and (27) Neguac.
The allocation of additional weight to cells located near the estuaries of largest rivers gives to the region of Bathurst an importance that approximately corresponds to its current population. The present situation of regional center now occupied by the town of TracadieSheila is also highlighted by the model. Finally, the predictions of this model overestimate the importance of what are now the villages of Leech/Pont-Lafrance and Price Settlement/Tabusintac. Taking into account smaller rivers along the coast would allow us to find most of the communities not yet identified in this region. In the East sector of the map, the model has found a number of sites where there were no significant settlements. The no occupying of these sites may be explained in part by the nature of the soil (several bogs), which our model did not take into account and the relative smallness of the present population of this region (about 70,000 people), which cannot occupy all a priori favorable sites. Also note that our model did not put forward sites like the one where is now located the town of Caraquet, whose site is identified by the letter C on Figure 2(b). Leaning against bogs, this town (including the village of Bas-Caraquet) is built on a plateau along an almost straight coastline and was once dubbed regionally the world’s longest village.
 (a)
(a) (b)
(b)
Figure 2. An application of our model to explain the present distribution of Northeastern New Brunswick population. On map (a), the height of each column is proportional to the power of attraction on people of the cell over which the column is built. Map (b) is the two-dimensional projection of map (a). The correspondence between numbers and place names is given in the text.
6. CONCLUSIONS AND DISCUSSION
In spite of the small number of factors contributing to the coastal peopling we have considered, we think that the above results prove the value of our mathematical model. Hence, the predictions for the Mediterranean region are almost perfectly consistent with that of its coastal peopling when the site effect was paramount. To describe the peopling of the North-East coast of New Brunswick, our initial model was modified to consider the ruggedness of a section of coast and to take into account middle size rivers. We were then able to match up the importance of almost all communities now living along this coastline.
The geometry of coastline and the nature of contact between land and water evolve with time and change the conditions of human occupation of the coasts. Looking backward, the application of our model to what was the coastline at different periods of prehistory could help to locate sites of human occupation of archaeological interest [6]. Looking forward, the contribution of external factors to the relation between communities and coastal areas increases and the factors bringing changes into the coastal systems come from increasingly far. Moreover, since the current sea level rise will seriously affect the coastal development in the decades to come, models of coastal peopling like ours could help to plan future movements of people now living along some parts of the world coastline. Using the internal factors associated with the future coastline deduced from hypsometric data, our model could determine the sites along the future coastal zone that are most likely to attract the future cities of social groups to be moved. The results of such a study could also help to plan the upcoming construction of major infrastructures expected to last a long period of time, such as highways, hospitals and universities.
Internal factors are easier to measure than external factors, because the latter depend on (individual or government) decisions often based on value judgments hard to predict and therefore to take into account in a model. But a model that does not consider important external factors will lead to predictions having little chance of realization. Therefore, one should consider the geographic area of influence of the social groups concerned, their means of communication, their population densities and their levels of social, economic and technological evolutions. The weight of the induced effect may in some cases be decisive. However, site effect will still be important because even in these cases it will serve as an amplifier of the induced effect. Choosing suitable settlement sites will thus always be highly desirable.
7. ACKNOWLEDGEMENTS
The authors are grateful to Dominique Bérubé and Marc Desrosiers, both at the Department of Natural Resources of New Brunswick in Bathurst, for the interest they brought to the present study and the coastline maps of the Acadian Peninsula they provided. They are also grateful to Solène Mallet Gauthier for her comments on the archaeological applications of this work.
REFERENCES
- UNESCO (1997) Land, sea and societies. In search of a sustainable balance: Environment and development of coastal regions and small islands. UNESCO, Paris.
- Corlay, J.-P. (1998) Factors and cycles of coastal occupation. In: Cabane, C., Chaussade, J., Corlay, J.-P., Miossec, A., Miossec, J.-M. and Pinot, J.-P., Eds., Géographie Humaine des Littoraux Maritimes, SEDES, Paris, 97-170.
- Liu, Y. (2009) Modelling urban development with geographical information systems and cellular automata. CRC Press, New York.
- McEvedy, C. (1985) Atlas of ancient history. Laffont, Paris.
- Landry, N. and Lang, N. (2001) Acadian history. Septentrion, Québec.
- Wheatley, D. and Gillings, M. (2002) Spatial technology and archaeology. The archaeological application of GIS. Taylor and Francis, New York. doi:10.4324/9780203302392

