Natural Science
Vol.4 No.11A(2012), Article ID:24877,5 pages DOI:10.4236/ns.2012.431119
Analytical solution of modified point kinetics equations for linear reactivity variation in subcritical nuclear reactors adopting an incomplete gamma function approximation
![]()
Nuclear Engineering Department, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil; *Corresponding Author: Halessandro@nuclear.ufrj.br
Received 5 September 2012; revised 10 October 2012; accepted 20 October 2012
Keywords: Accelerator-Driven System; Subcritical Reactors; Point Kinetics Equations; Incomplete Gamma Functions
ABSTRACT
The present work aims to achieve a fast and accurate analytical solution of the point kinetics equations applied to subcritical reactors such as ADS (Accelerator-Driven System), assuming a linear reactivity and external source variation. It was used a new set of point kinetics equations for subcritical systems based on the model proposed by Gandini & Salvatores. In this work, it was employed the integrating factor method. The analytical solution for the case of interest was obtained by using only an approximation which consists of disregarding the term of the second derivative for neutron density in relation to time when compared with the other terms of the equation. And also, it is proposed an approximation for the upper incomplete gamma function found in the solution in order to make the computational processing faster. In addition, for purposes of validation and comparison a numerical solution was obtained by the finite differences method. Finally, it can be concluded that the obtained solution is accurate and has fast numerical processing time, especially when compared with the results of numerical solution by finite difference. One can also observe that the gamma approximation used achieve a high accuracy for the usual parameters. Thus we got satisfactory results when the solution is applied to practical situations, such as a reactor startup.
1. INTRODUCTION
During the operation of a nuclear reactor it’s essential to know the behavior of the nuclear core. The point kinetics equations are a way to describe the time behavior of the neutron density and consequently the criticality in nuclear reactors. These quantities are essential to understand and predict the behavior of a nuclear reactor during its start-up, when the control rods are raised and the reactivity in the system increases. So, the analytical solution of point kinetics equations with a group of delayed neutrons is extremely useful to predict neutron density variation during the nuclear reactor start-up.
In particular, for subcritical reactors, the point kinetics equations are fundamental to continuously monitor the behavior of the reactivity for a possible variation of the intensity of external sources. And, studying subcritical reactors is very important due to the fact that they are very promising and innovative reactors, not only for power generation, but also for the transmutation of heavy elements with large half-life, reducing radioactive material’s inventory. With the development of a new generation of subcritical reactors such as ADS, predicting power and reactivity transients in a fast and accurate way becomes necessary in the event of a possible variation in the intensity of external sources.
Considering that, this work aims to achieve an analytical approximation to predict the behavior of neutron density in subcritical systems, such as ADS reactors. To achieve this it was adopted the new formulation of point kinetics equations for subcritical systems proposed by Gandini & Salvatores [1].
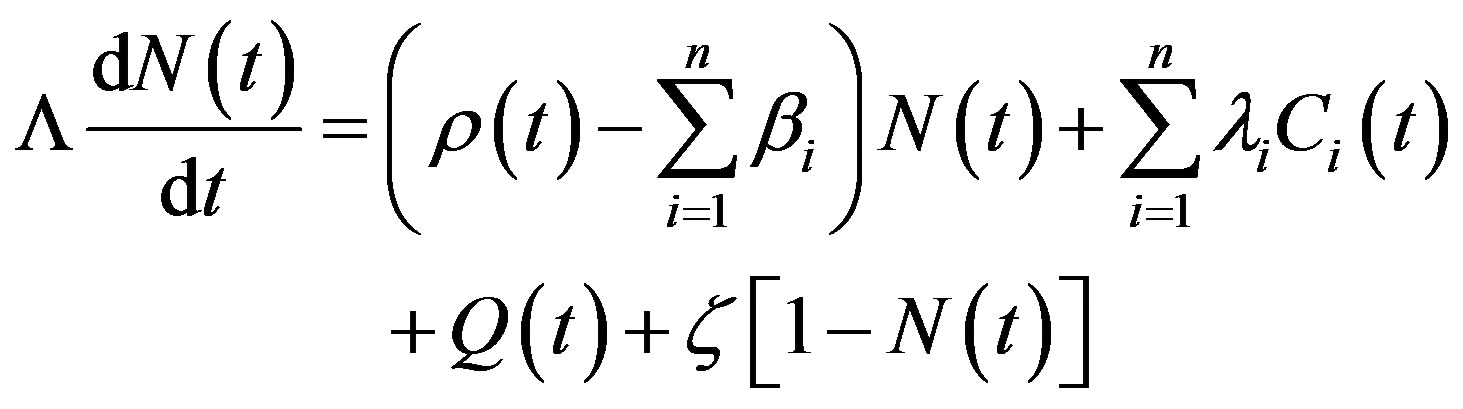
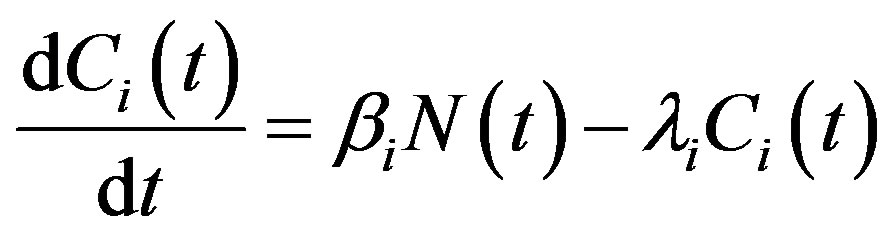

Considering a single group of precursors, the mathematical formulation becomes:
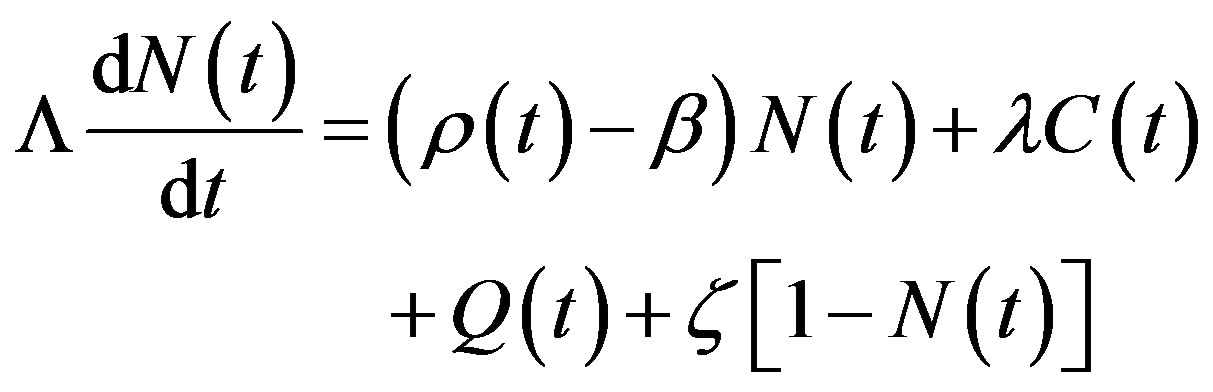 (1)
(1)
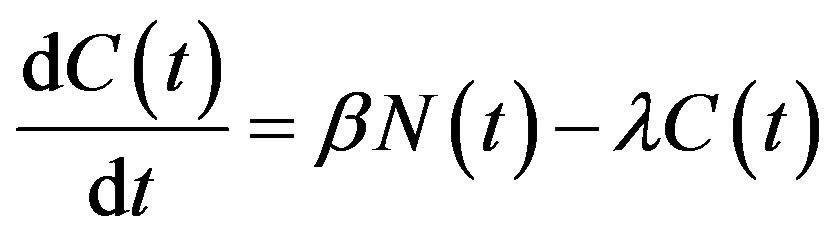 (2)
(2)
subjected to the initial conditions:
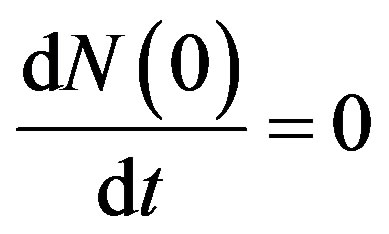 (3)
(3)
 (4)
(4)
2. MATHEMATICAL FORMULATION
Differentiating Eq.1 in relation to time one can write:
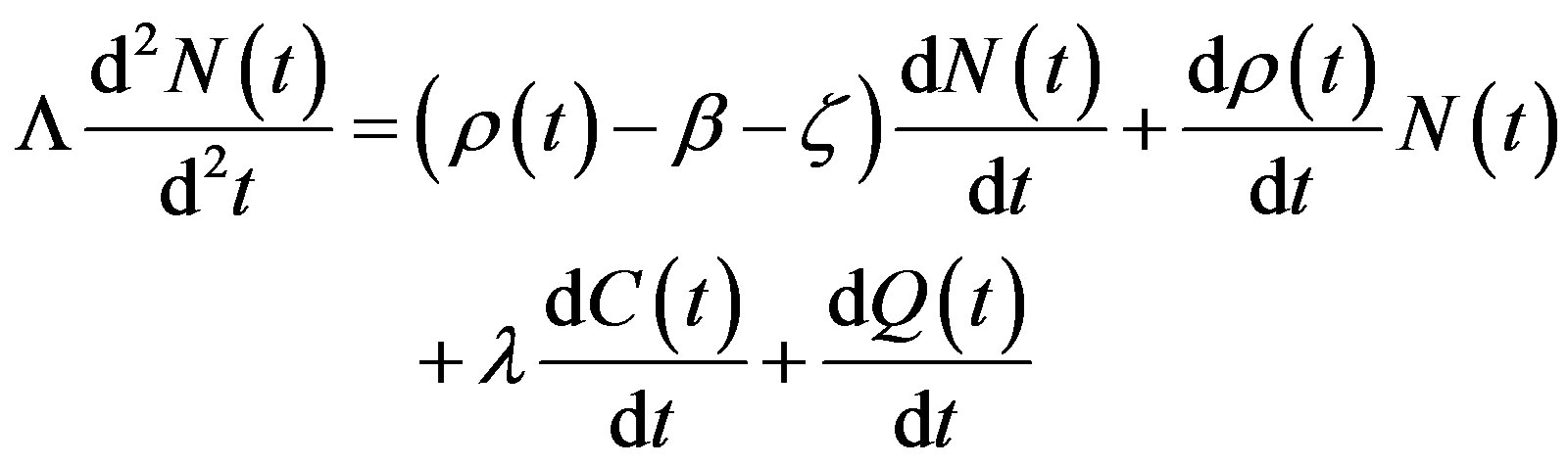 (5)
(5)
Replacing Eq.2 in Eq.5 one obtains:
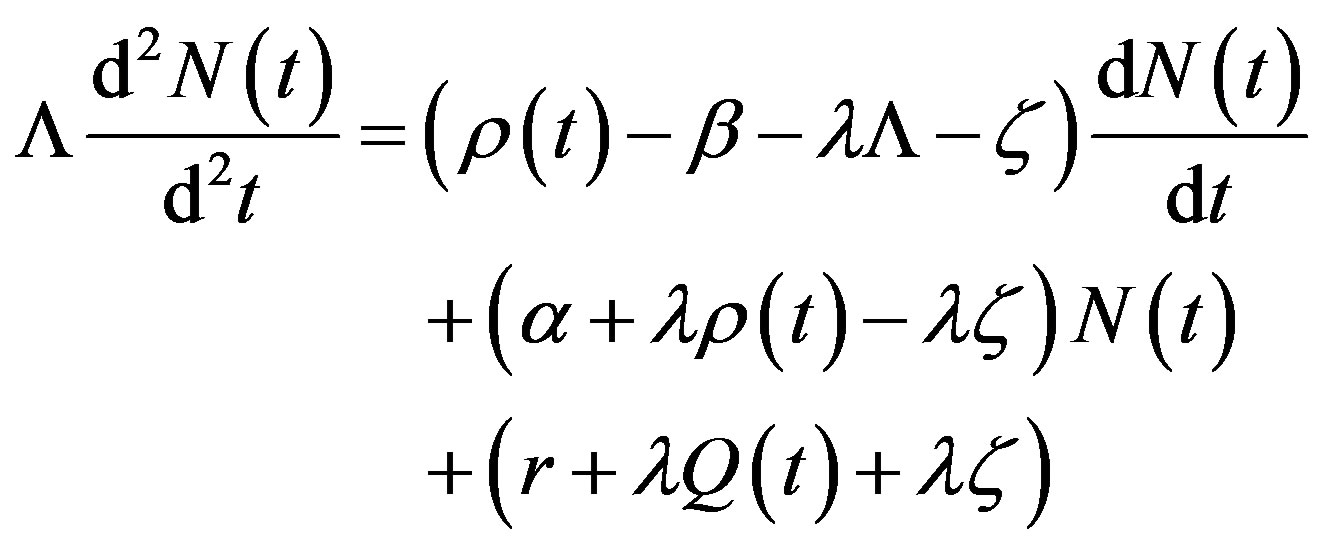 (6)
(6)
2.1. Type of External Source and Reactivity
The goal of this work is to study the behavior of the neutron density in subcritical systems considering an insertion of reactivity in the system that varies in a linear manner in time according to the expression:
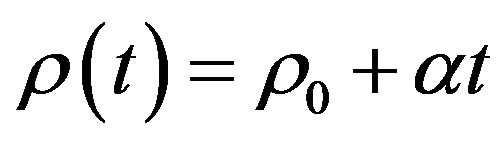 (7)
(7)
where  is the initial reactivity in the system
is the initial reactivity in the system 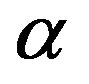 and is the linear reactivity insertion rate.
and is the linear reactivity insertion rate.
In this work it will be also considered an external neutron source that linearly varies according to the expression:
 (8)
(8)
where  is the initial intensity of the source and r is the linear insertion rate for external neutrons.
is the initial intensity of the source and r is the linear insertion rate for external neutrons.
The fact that both the external neutron source and the reactivity behave with linear variation is extremely relevant because not only can they behave exactly that way but also any kind of behavior can be approximated to a linear type in a small time interval. Thus the solution obtained in this work can be applied to any case as long as a small period of time is taken.
2.2. Analytical Approximation
For purposes of validation and comparison a numerical solution of point kinetics equations for subcritical systems was obtained by the finites differences method considering a group of delayed neutrons precursors as represented in Eqs.1 and 2.
It was used the following expressions to implement the implicit temporal integration method:
 (9)
(9)
 (10)
(10)
In all validations the mesh point h = 10−5 s was used.
Using the nuclear parameters shown in Table 1 and the numerical solution obtained and fitting an polynomial function of degree 5 on the graphic of neutron density by time it was observed that the term  in Eq.6 was much smaller in magnitude than the others terms in the equation, as can be seen in Figure 1.
in Eq.6 was much smaller in magnitude than the others terms in the equation, as can be seen in Figure 1.
In Figure 1, it was used the following definitions from Eq.6:
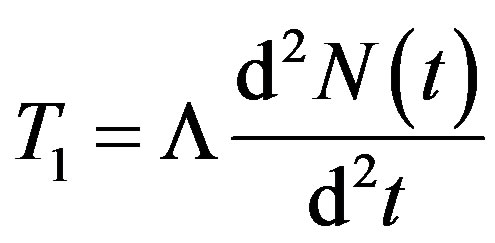
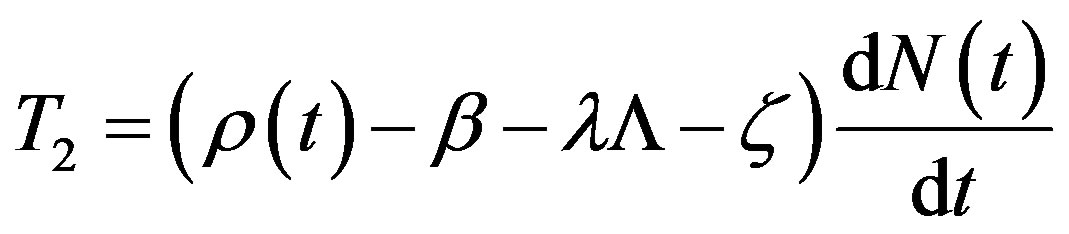
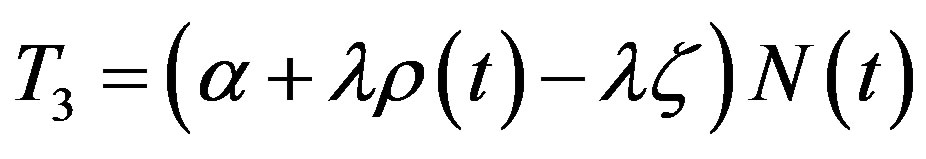
So, it could be concluded that disregarding the term in Eq.6 in relation to all the others in the equation is a valid approximation [2].
2.3. Final Solution
Applying the aforementioned approximation, Eq.6 can be written as the nonhomogeneous differential equation:
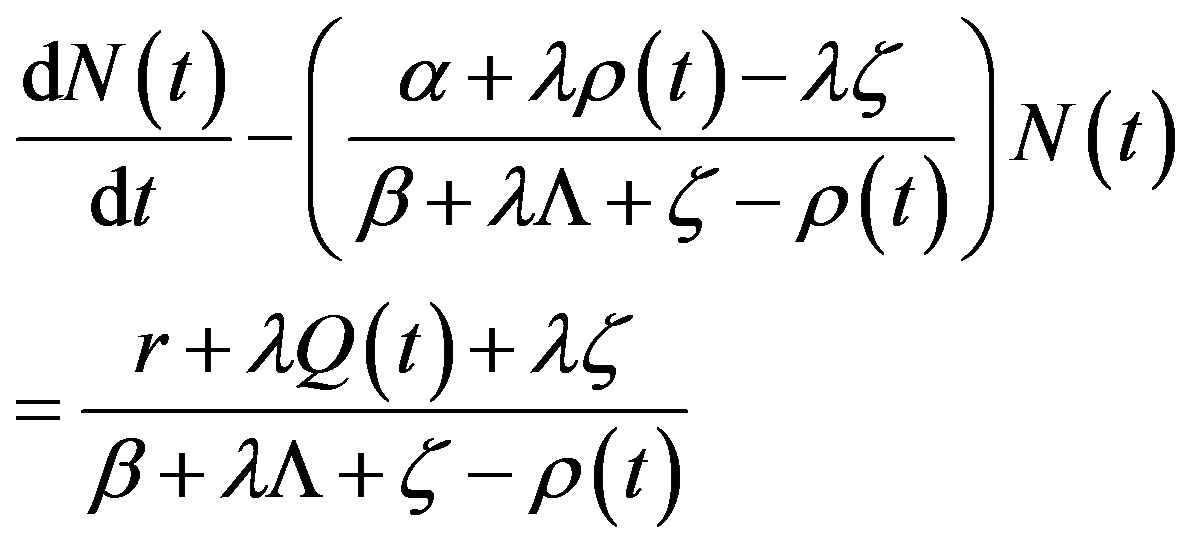 (11)
(11)
That can be rewritten as:
 (12)
(12)

Figure 1. Comparison among the terms involving neutron density in Eq.6 using the nuclear parameters in Table 1.
where:

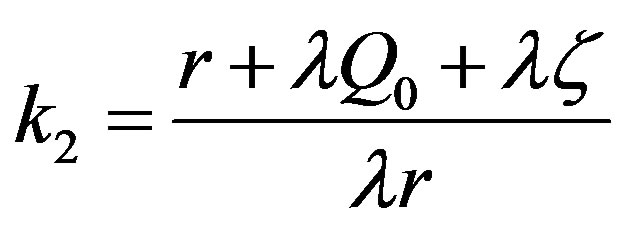

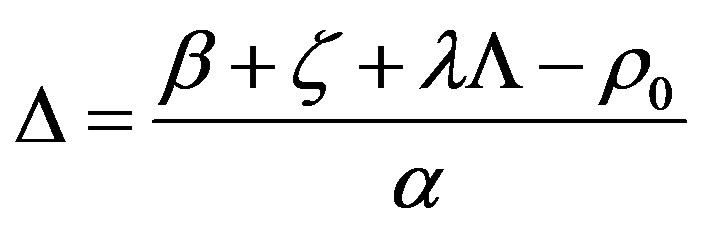
Using the integrating factor method, as shown in Appendix A, it can be achieved the following expression for neutron density:
 (13)
(13)
Imposing the initial conditions expressed by Eqs.3 and 4, one can obtain that:
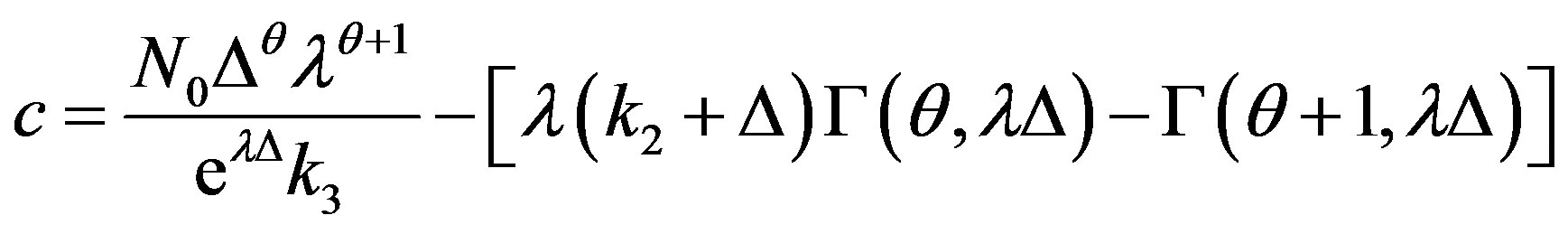 (14)
(14)
where:
 (15)
(15)
By defining the following constants:
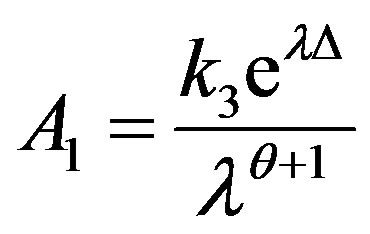
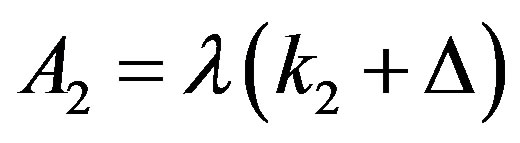

one can achieve the following solution:
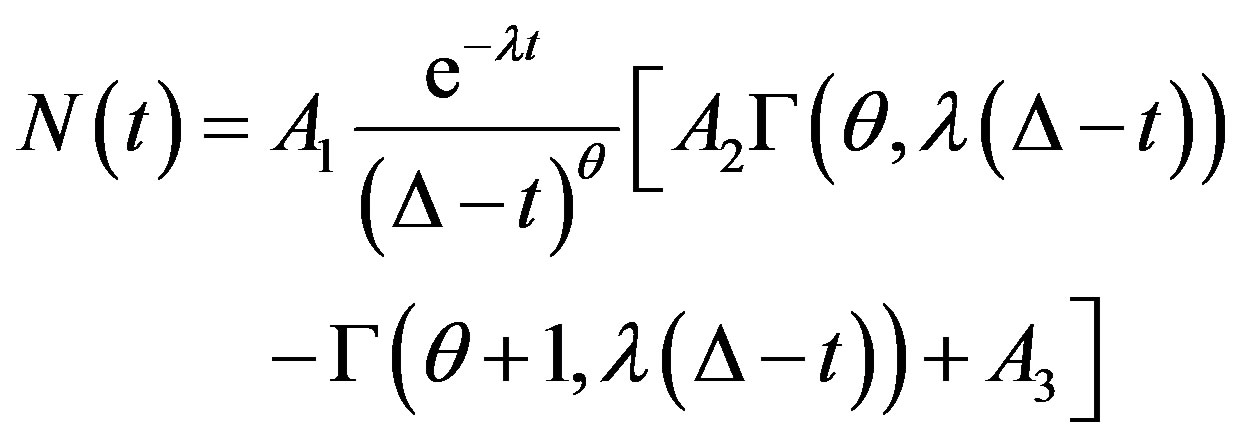 (16)
(16)
Applying the following corollary of Incomplete Gamma functions

on Eq.16, it can be grouped in a more convenient manner, expressed in Eq.17.
 (17)
(17)
And also, the constant 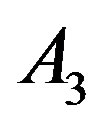 can be rewritten as:
can be rewritten as:
 (18)
(18)
2.4. An Approximation for Incomplete Gamma Function
The incomplete gamma function found in the neutron density function, written by Eq.17, can be approximated with no significant accuracy loss. To achieve that, the following gamma function definition will be used [3]:
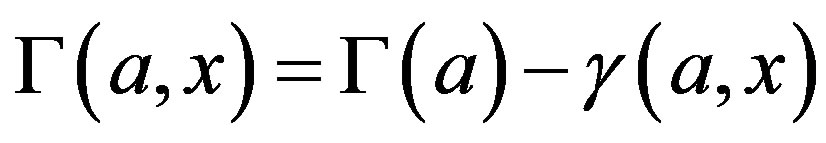 (19)
(19)
In a recent paper, Haglund, J. [4] showed a series expansion for the lower incomplete gamma function. Using this series expansion in Eq.23, one can achieve:
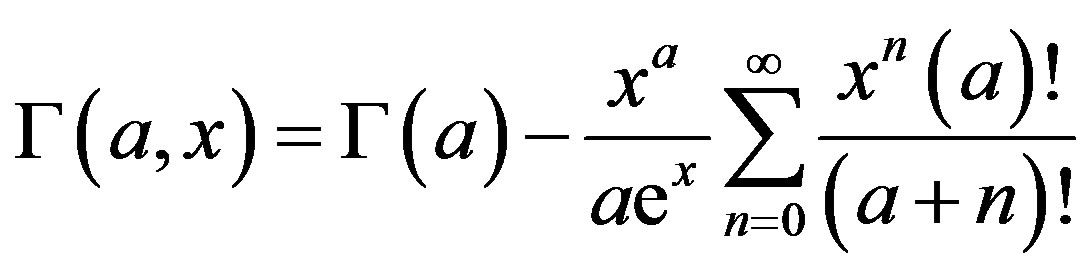 (20)
(20)
It was observed that for the usual subcritical parameters taking 16 terms in this expansion give us a good accuracy.
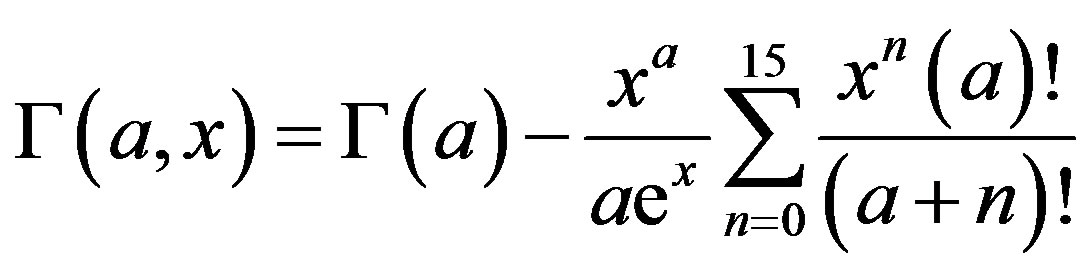 (21)
(21)
By using the gamma function approximation proposed by Nemes [5], one can achieve an approximation for the upper gamma function, as follows:
 (22)
(22)
Again using the nuclear parameters shown in Table 1, it could be observed that the absolute deviation between
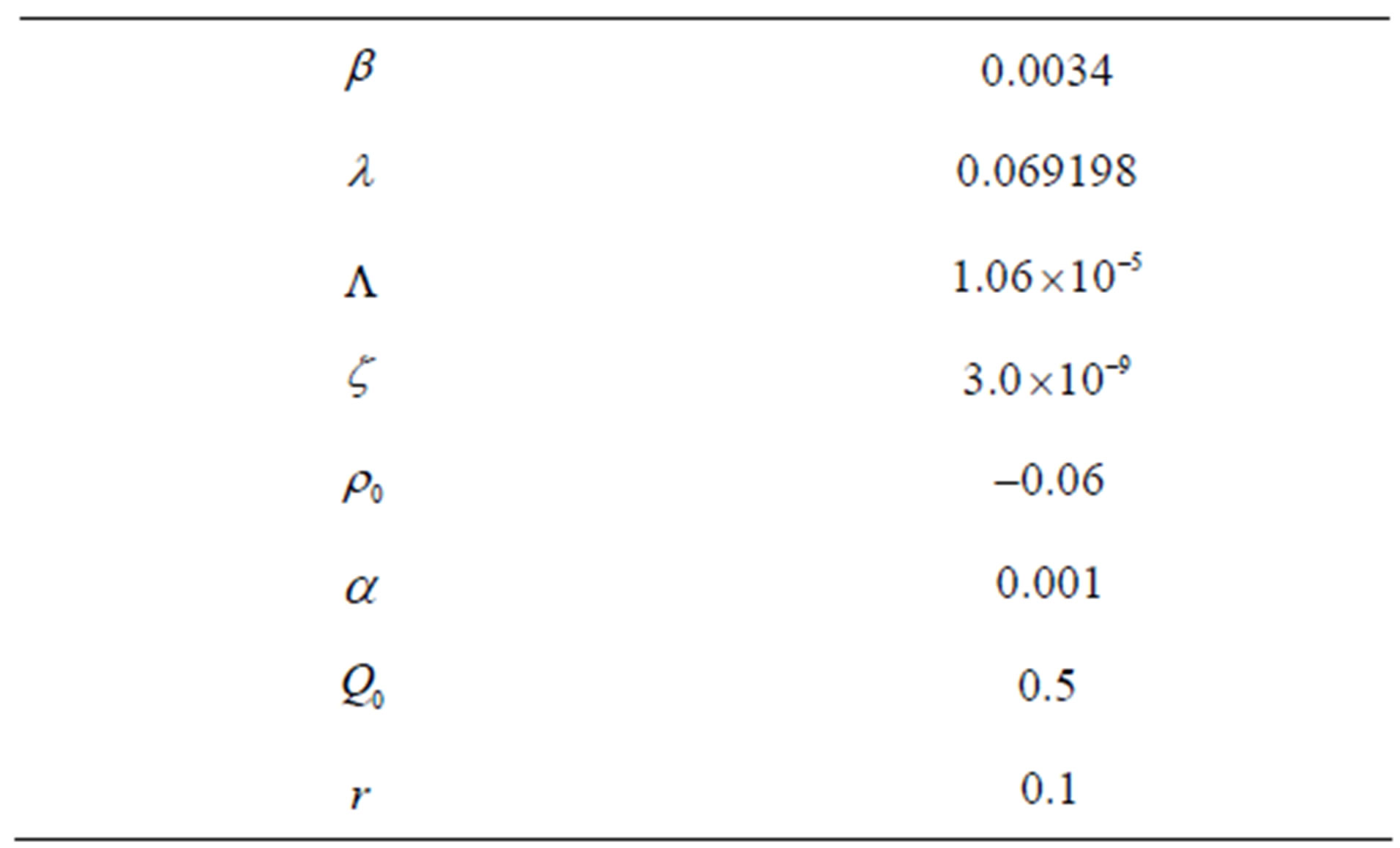
Table 1. Kinetics and others parameters.
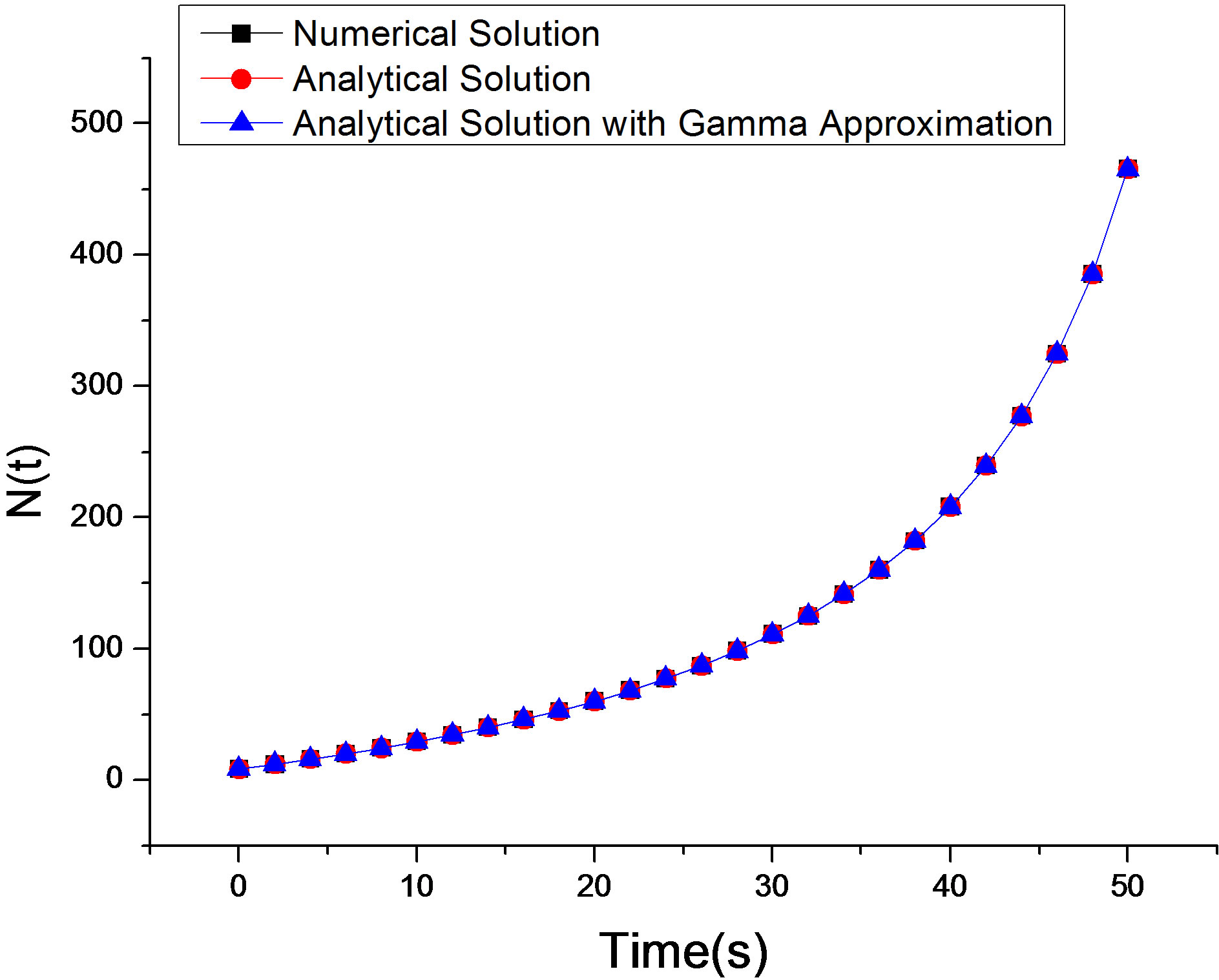
Figure 2. Comparison among the calculation methods of neutron density.
the real value of the incomplete gamma function and its value using the approximation expressed in Eq.22 was at most 0.689% at 0 s.
3. RESULTS
In Table 1, it is shown the nuclear parameters that were used to test the solution obtained in this paper.
Figure 2 shows a comparison among the solutions obtained by the analytical method proposed in this article with and without the gamma function approximation and by the finite difference method.
From Figure 2, it can be concluded that the analytical solution with the approximation proposed coincides with the numerical reference method. Further analysis shows that the absolute value of relative deviation between them doesn’t exceed 0.00165% in the first fifty seconds. This conclusion can be justified by the fact that the common values of Λ for subcritical reactors are smaller than for critical reactors such as PWRs, showing that disregarding the second derivative term from Eq.6 is a good approximation.
4. CONCLUSION
An analytical approximation was developed in order to predict the behavior of neutron density in subcritical systems with linear reactivity insertion and external source of neutrons variation. The mathematical formulation proposed was achieved by solving the point kinetics equations for subcritical systems with a single group of precursors and by adopting an approximation for the gamma function. The results obtained have been really accurate with small relative deviations when compared to the ones from the reference method, which was the numerical solution by finite differences.
5. ACKNOWLEDGEMENTS
The authors acknowledge the support provided by CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) in the development of this research.
REFERENCES
- Gandini, A. and Salvatores, M. (2002) The physics of subcritical multiplying systems. Journal of Nuclear Science and Technology, 6, 673-686. Hdoi:10.1080/18811248.2002.9715249
- Palma, D., Martinez, A.S. and Gonçalves, A.C. (2009) Analytical solution of point kinetics equations for linear reactivity variation during start-up of a nuclear reactor. Annals of Nuclear Energy, 36, 1469-1471. Hdoi:10.1016/j.anucene.2009.06.016
- Arfken, G. (1985) Mathematical methods for physicists. Academic Press, Waltham.
- Haglund, J. (2011) Some conjectures on the zeros of approximates to the Riemann ≡-function and incomplete gamma functions. Central European Journal of Mathematics, 9, 302-318. Hdoi:10.2478/s11533-010-0095-3
- Nemes, G. (2010) New asymptotic expansion for the Gamma function. Archiv der Mathematik, 95, 161-169.
- Gradshteyn, I.S. and Ryzhik, I.M. (2007) Table of integrals, series and products. Academic Press, California.
APPENDIX A
The following equation, Eq.12, can be solved by the integrating factor method [6].

Using this method in the differential Eq.12 one can obtain:
 (A.1)
(A.1)
where the integrating factor is:
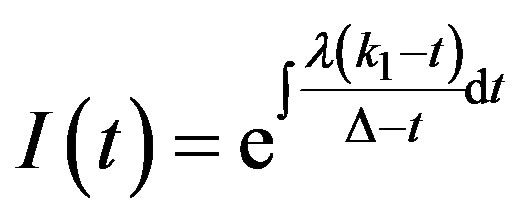
In replacing variables  and defining
and defining  one can find:
one can find:
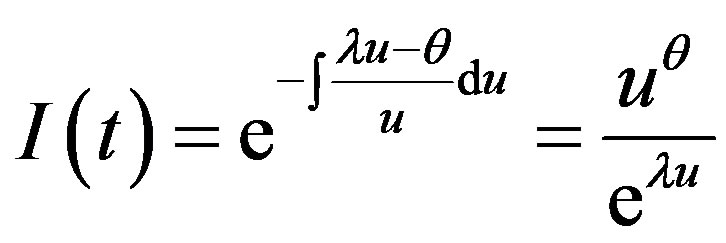 (A.2)
(A.2)
Thus, by the integrating factor method used in Eq.A.1 it can be provided solutions represented by:
 (A.3)
(A.3)
Both integrals in Eq.A.3 are tabled [6] and produce the following expression for neutron density:
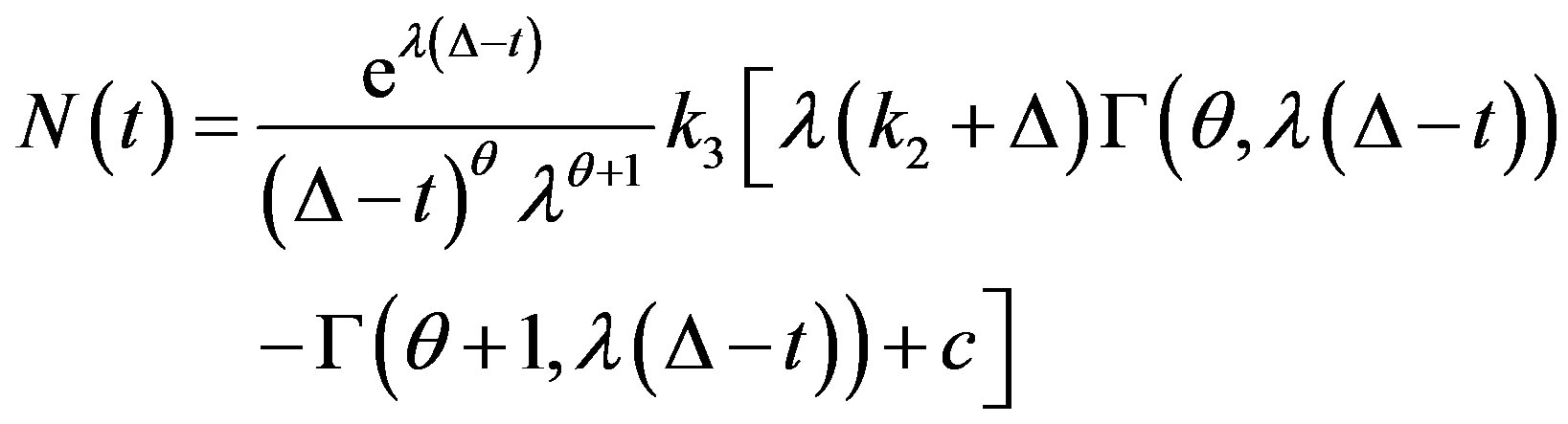 (A.4)
(A.4)

