Health
Vol.06 No.21(2014), Article ID:52502,12 pages
10.4236/health.2014.621324
On the Role of Consumer Preferences in the Coordination among Health Insurers under Regulated Competition
Jana Vyrastekova1, Ferdy van Beest2, Christiaan Lako3, Esther-Mirjam Sent1
1Department of Economics, Nijmegen Center for Economics, Institute for Management Research (IMR), Radboud University, Nijmegen, The Netherlands
2Department of Financial Accounting and Reporting, Nyenrode Business University, Breukelen, The Netherlands
3Department of Public Administration, Radboud University, Nijmegen, The Netherlands
Email: J.Vyrastekova@fm.ru.nl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 September 2014; revised 9 November 2014; accepted 23 November 2014
ABSTRACT
This paper addresses the coordination problem of price and quality setting insurers, arising on the health insurance market under regulated competition, as introduced, for instance, in the Netherlands in 2006. We use an experimental study to gain novel insights on the impact of the uncertainty about consumer preferences on the coordination problem. This fundamental uncertainty implies uncertainty about the identity of the payoff dominant equilibrium, while the risk dominant equilibrium is independent of the state of the world. The experimental results show that insurers are more likely to coordinate on the payoff dominant equilibrium under incomplete information. When insurers face not only strategic but also fundamental uncertainty in the coordination problem, they delay the response to the risk dominant strategy, and persist longer in trying to coordinate on the payoff dominant equilibrium. For the market we study, this implies that the coordination under incomplete information will result in consumers paying higher prices, in contrast to the original objectives of the regulated competition.
Keywords:
Health Insurance, Regulated Competition, Coordination, Information Concerning Consumer Preferences, Laboratory Experiment

1. Introduction
With the introduction of the Health Insurance Act in the Netherlands in 2006, insurance companies are expected to compete on price and quality settings in a regulated competition [1] . However, as a result of uncertainty concerning consumer preferences, insurance companies face difficulties in their coordination strategies tying customers to their company and providing them with the most optimal insurance product.
Coordination problems are at the core of such important economic phenomena as bank runs, currency rises, and management failures [2] - [4] . We identify managed competition among health insurers [5] as another example where coordination problems arise. They affect insurers, prohibited to discriminate among consumers, who simultaneously choose price and quality of their product. The consumers are obliged to purchase one of the available products, and evaluate the price-quality tradeoff whenever supply varies across price and quality. This results in coordination problems, as insurers may share the market by offering the same product, and multiple equilibria exist, each with another price and quality offered.
The goal of introducing managed competition on the health insurance market is to achieve the lowest possible price and quality as high as possible at this price. In our model, such low-price/high-quality equilibrium co-ex- ists with other equilibria, giving a higher payoff to the insurers, thus generating lower consumer surplus. Moreover, the low-price/high-quality equilibrium of the static game is less risky from a strategic uncertainty perspective than the payoff dominant equilibrium. Behavioral research on coordination games, however, does not give clear guidance as to which of these equilibria will be played.
The tension of selecting between a payoff dominant Nash equilibrium and a risk dominant Nash equilibrium [6] [7] is embodied in a stag hunt game. Deductive arguments can be made for both of them, but they seem not to be strong enough―or unique―in affecting players’ behavior. Subjects have been observed to play the risk dominant equilibrium in some studies on coordination games [8] -[10] , but in others, they manage to coordinate on the payoff dominant equilibrium [11] [12] .
Recently, the prevalence of the payoff dominant equilibrium has been linked to the payoff foregone if its choice results in miscoordination. The more costly the coordination mistake is, the less likely the survival of the payoff dominant equilibrium is [11] . In [13] , the authors identify a similar mechanism in a minimum-effort game, adding a cost of effort increasing in the effort which does not change the set of Nash equilibria of the game. It turns out that subjects are sensitive to the cost structure of their strategic errors, and converge to the payoff dominant equilibrium only when overshooting is relatively less costly than undershooting. In a similar vein, subjects were found to be able to “creep up” towards the most efficient equilibrium over time, exploring the neighborhood of the initial group position [14] , when the strategy space is finer, so that mistakes in this process are less costly. This evidence reinforces the idea that deductive reasoning guides behavior to a lesser extent than inductive reasoning, driven by the past observations [15] . Moreover, next to such backwards looking behavior, the role of forward-looking players in this process has also been stressed, suggesting that some players try to teach others to sustain payoff dominance [16] .
The coordination problem arising in our model of managed competition stems from two insurers simultaneously choosing price and quality on a binary scale. Under complete information about consumer preferences, two of the available strategies in the 4 × 4 game are strictly dominated. The remaining 2 × 2 game has a character of a stag hunt game, with a risk dominant equilibrium in which both insurers offer high quality product for low price. The alternative equilibrium strategy depends on the fraction of the consumers preferring high-price/ high-quality product over low-price/low-quality product. Interestingly, this alternative equilibrium is payoff dominant from the insurers’ perspective. From the perspective of the consumer welfare, however, the payoff dominant equilibrium offers a worse outcome than the risk dominant equilibrium, a product with either higher price of lower quality than the risk dominant equilibrium.
Our study offers insight on the welfare implications of the simultaneous price/quality choice in a market with managed competition. Is it likely that insurers coordinate on the risk dominant equilibrium, with positive welfare implications for the consumers? Or should we expect that they manage to coordinate on the payoff dominant equilibrium with lower consumer welfare, failing thus the objectives of the managed competition?1
To address these questions, we present data on two complete information treatments, CI-quality treatment and CI-price treatment, representing two extreme parameterizations of our coordination game with respect to the consumers’ willingness to pay for quality. And, we also collect data in a treatment when consumer preferences are not known by the insurers, as in our Incomplete information (II) treatment. This last treatment is most likely to correspond to the coordination problem faced by the insurers in the actual markets. Under incomplete information, the identity of the payoff dominant equilibrium depends on the consumer preferences, and thus on the beliefs of the insurers. In the coordination problem, incomplete information about consumer preferences thus adds fundamental uncertainty about the state of the world on top of the strategic uncertainty. Will it affect the coordination problem towards choosing the safer, risk dominant strategy?2
Surprisingly, the answer to this question is no. Our paper provides a novel insight―how adding fundamental uncertainty about the identity of the payoff dominant equilibrium helps players to coordinate on this equilibrium rather than preventing them. We propose that the mechanism underlying our data is that players respond less immediately to the past observations of the risk dominant strategies under incomplete information than under complete information. By persisting longer with playing the strategy they believe to be payoff dominant, the players are in the end more likely to coordinate on the payoff dominant equilibrium. This is possibly due to the fact that observing the risk dominant equilibrium under incomplete information is not necessarily an expression of mistrust, preventing coordination on the payoff dominant equilibrium, but possibly an expression of uncertainty as to which strategy corresponds to the payoff dominant equilibrium. Such uncertainty of how to interpret observation of a risk dominant strategy does not persist under complete information.
In Section 2, we now briefly outline our model and the experiment design. Section 3 summarizes the results. We discuss our observations in Section 4, and conclude in Section 5.
2. Model and Experiment Design
2.1. Model
The regulated market for health insurance is modeled as a duopoly with insurers simultaneously choosing price and quality. When insurers only choose price, the logic of Bertrand competition predicts that they end up pricing their products at the marginal cost. However, when quality is chosen simultaneously as well, undercutting the price does not necessarily increase demand if the quality of the competitor is higher.
To capture this coordination problem so that can be implemented in the laboratory, insurers choose either price H or L, with 0 < L < H; and either quality A or B. The costs satisfy c(A) > c(B) > 0, and L > c(A), so that each price-quality combination is feasible without losses. Each insurer is restricted to only one product type, in accordance no discrimination among consumers under regulated competition. Insurers thus choose one of four strategies: LA, HA, LB, or HB.
The profit of insurer I = 1, 2, offering price pi and quality qi is given by pI = ni (piqi; pjqj)(pi − c(qi)), where ni (piqi; pjqj) is the demand for insurer i’s product piqi, when the other insurer offers pjqj. Each consumer is obliged by the law to purchase one unit of insurance, so that ni (piqi; pjqj) + nj (piqi; pjqj) = N, where N is the number of consumers. We assume that insurers can satisfy any demand they attract.
Insurer’s demand depends on the strategies of both insurers. When insurers choose the same price and quality, each serves half of the market. This assumption excludes that reputation, brand name, loyalty, etc. player a role for the consumers. We do not argue that they do not affect consumers, but eliminating them allows us to focus on coordination problem. When insurers do not choose the same strategy, two situations can arise. When their strategies differ only on one of the dimensions, consumers can rank the products, and they choose the product with lower price (when quality is the same); or higher quality (when price is the same).
An interesting situation arises when consumers have to choose between products that differ on both dimensions, i.e. between product HA and LB. One might imagine, for example, that young, healthy, or low-income individuals would prefer low price over high quality and choose LB, while older, chronically ill, or high income individuals would prefer high quality over low price and choose HA. Let us denote by 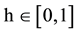 the fraction of consumers that prefers HA over LB. Consequently, demand of insurer with strategy HA when the other insurer chooses LB is given by hN, while the demand by the other insurer is (1 − h)N.
the fraction of consumers that prefers HA over LB. Consequently, demand of insurer with strategy HA when the other insurer chooses LB is given by hN, while the demand by the other insurer is (1 − h)N.
With respect to consumers, we assume that each consumer k = 1,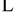 , N observes the products offered by insurer i and j and purchases insurance (pk, qk). With probability
, N observes the products offered by insurer i and j and purchases insurance (pk, qk). With probability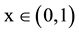 , the consumer then faces insurance event implying cost d > 0. This cost is fully insured, but only if the consumer purchased insurance of quality A. The expected payoff of consumer k is uk (pk, qk) = E − pk − xdk where E > 0 is the initial wealth of the consumer, dk = 1 if qk = B, and dk = 0 if qk = A. A risk neutral consumer prefers LB over HA iff E − L − xd > E − H. The experiment parameterization is given in Table 1. It is chosen so that a risk neutral and risk averse consumers prefer HA over LB.
, the consumer then faces insurance event implying cost d > 0. This cost is fully insured, but only if the consumer purchased insurance of quality A. The expected payoff of consumer k is uk (pk, qk) = E − pk − xdk where E > 0 is the initial wealth of the consumer, dk = 1 if qk = B, and dk = 0 if qk = A. A risk neutral consumer prefers LB over HA iff E − L − xd > E − H. The experiment parameterization is given in Table 1. It is chosen so that a risk neutral and risk averse consumers prefer HA over LB.
The quality and price setting coordination game between insurers with complete information about the consumer demand (value of h) is given in Table 2(a). Table 2(b) contains parameterization of the game we used in our experiment. This static game was repeated in the experiment for 15 periods in the same pair of players.
When information about the preferences of the consumers is incomplete, we make a standard assumption that the insurers have the same information about the market, which is represented by the same probability distribution over the possible value of the parameter . Let us denote by h’
. Let us denote by h’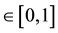 the expected value of h under these beliefs. Consequently, the Bayesian normal form game that the insurers play under incomplete information about consumer preferences can be obtained from game in Table 2(a) by replacing parameter h by its expected value h’.
the expected value of h under these beliefs. Consequently, the Bayesian normal form game that the insurers play under incomplete information about consumer preferences can be obtained from game in Table 2(a) by replacing parameter h by its expected value h’.
Let us now state lemmas that describe the equilibria for the static game implemented in the experiment, when played under complete (and incomplete) information, as well as the subgame perfect Nash equilibria in the repeated game. All straightforward proofs of these lemmas can be obtained from the corresponding author upon request.
Lemma 1:
The game in Table 2(b) has two pure strategy Nash equilibria: (1) (LA, LA), (2a) (LB, LB) if h < 2/5, (2b) (HA, HA) if h > 2/5.
We find that (LA, LA) is a Nash equilibrium for all values of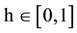 . It co-exists with an alternative equilibrium, that depends on the characteristics of the demand. When sufficiently many consumers are willing to pay for quality (h > 2/5), then (HA, HA) is an equilibrium; otherwise (h < 2/5), (LB, LB) is an equilibrium. In both cases, this alternative equilibrium is payoff dominant for the insurers, and less favorable for the consumers. Moreover, consider that insurers selecting between the equilibrium strategy LA and the alterative equilibrium strategy (LB or HA) face strategic uncertainty. When we assume that they assign equal probability to either equilibrium strategy to be chosen by the other player3, and probability zero to the non-equilibrium strategies, then the expected payoff of LA is 1.5 while the expected payoff of the alternative equilibrium strategy is lower than that, either 1 (for h < 2/5) or 1.25 (for h > 2/5). This implies that the strategic risk associated with choosing the equilibrium strategy LA is lower than risk associated with the alternative equilibrium strategy, albeit it forms the payoff dominant equilibrium. The situation faces by insurers thus for any value of h results in a tradeoff between risk and payoff dominance, similar to the stag hunt game.
. It co-exists with an alternative equilibrium, that depends on the characteristics of the demand. When sufficiently many consumers are willing to pay for quality (h > 2/5), then (HA, HA) is an equilibrium; otherwise (h < 2/5), (LB, LB) is an equilibrium. In both cases, this alternative equilibrium is payoff dominant for the insurers, and less favorable for the consumers. Moreover, consider that insurers selecting between the equilibrium strategy LA and the alterative equilibrium strategy (LB or HA) face strategic uncertainty. When we assume that they assign equal probability to either equilibrium strategy to be chosen by the other player3, and probability zero to the non-equilibrium strategies, then the expected payoff of LA is 1.5 while the expected payoff of the alternative equilibrium strategy is lower than that, either 1 (for h < 2/5) or 1.25 (for h > 2/5). This implies that the strategic risk associated with choosing the equilibrium strategy LA is lower than risk associated with the alternative equilibrium strategy, albeit it forms the payoff dominant equilibrium. The situation faces by insurers thus for any value of h results in a tradeoff between risk and payoff dominance, similar to the stag hunt game.
Finally, let us describe the subgame perfect Nash equilibrium of the finitely repeated game. Naturally, any sequence of the stage game Nash equilibria is a part of subgame perfect Nash equilibrium of the finitely repeated game. However, due to the multiplicity of the stage game Nash equilibria, there also equilibria feasible in the finitely repeated game, where the strictly dominated strategy HB is played in early periods. We refer to them as collusive equilibria, because they yield a higher payoff to the insurers, and they require enforcement by trigger strategies.
Lemma 2:
The following trigger strategy στ represents a class of subgame perfect Nash equilibrium strategies that differ only in the length of the cooperative phase, denoted by τ, during which the players choose HB. It holds that 1 ≤ τ ≤ Tmax. The strategy στ is as follows: (1) play HB in period 1. (2) If the observed strategy combination in any period 1 ≤ t' < t was (HB, HB), then play HB if t ≤ τ; play LB if t > τ and h < 2/5; and play HA if t > τ and if h > 2/5. (3) Play LA in any other case not mentioned in (1) or (2). For T = 15, as in the experiment, the value Tmax = 12 for h < 2/5, and Tmax = 13 for h > 2/5.
According to this lemma, insurers can sustain collusion offering a low quality at a high price (HB) in a subgame perfect Nash equilibrium of the finitely repeated game, at least for a certain period of time. The maximal length of sustaining collusion is 12 (13) periods out of 15 periods, for h < 2/5 (h > 2/5). It is sustained by the threat of switching to stage game Nash equilibrium strategy LA if anyone deviates from strategy HB before the
Table 1. Experiment parameterization.
Table 2. Payoff matrix. (a) General; (b) Experiment parametrization.
collusive phase ends. This result suggests that besides the coordination problem arising in the one-shot game, the repeated interaction brings the threat of tacit collusion, with even more damaging strategies from the consumers’ perspective, with high prices and low quality offered on the regulated market.
2.2. Experiment Design
We investigate the duopoly market described above by incentivized economic experiments. In total 82 students of economics, business, and other social sciences, age between 18 and 24, were recruited using the computerized system ORSEE and invited to the NSM Decision Lab at Radboud University Nijmegen, the Netherlands. Each subject participated in only one experimental session. The language of the experiments was English. Instructions are available from the corresponding author at request. Upon arrival, participants were randomly assigned to a computer terminal, and interacted anonymously. The software was programmed using z-Tree [23] . The experiment instructions were read aloud to the subjects and a short understanding test was administered. When all subjects answered correctly, the experiment started. The sessions took around one hour, and subjects received all their earnings in private at the end of the experiment, amounting on average to 12.60 Euro (including a 3 Euro participation fee).
We implemented two experimental treatments. In both of them, the subjects interacted as insurers, setting simultaneously their price and quality of the product. In the Incomplete information treatment, moreover, some subjects were also assigned to the role of consumers, and their preferences over the price/quality trade-off were a priori not known to the insurer subjects. There were either 4 or 8 consumers in the duopoly, and the exchange rate for experimental tokens of the insurer players was scaled up by 2 in the markets with four consumers compared to the markets with eight consumers, so that the expected earnings of the insurance players were unaffected by the number of consumer players.
In the Complete information treatments, the insurers were informed about the characteristics of the demand. This demand was simulated and the insurer subjects were informed about that. We implemented two extreme parameterizations of the demand: one in which all consumers solve the trade-off between quality and price by choosing quality over price (CI-quality treatment with h = 1, see Section 2.1), and one by choosing price over quality (CI-price treatment with h = 0, see Section 2.1). In Table 3, we provide information about the number of duopoly markets in each treatment, and number of consumers in the Incomplete information treatment. Subjects were assigned at random to treatments, and each subject participated in only one of them.
The subjects interacted repeatedly in the same duopoly market for 15 rounds and remained in the same role for all rounds (in the Incomplete information treatment). At the end of each round, subjects received feedback about their earnings. The insurers learned the decision made by the other insurer, as well as the number of consumers that chose his/her product, but the consumers did not learn anything about decisions of other consumers.
Because insurers in the Incomplete information treatment did not know the preferences of consumers, we also collected the insurers’ beliefs with respect to the consumers’ preferences. In particular, we asked them whether they expect that more or less than half of the customers prefer a high price and high quality product (HA) over a low price and low quality product (LB). We use this information in the analysis to interpret the product positioning of the insurers in the Incomplete information treatment, and compare the insurer strategies in the Incomplete information treatment with the relevant Complete information treatment.
3. Results
We find that in both Complete information treatments, see Figure 1(a) for CI-price treatment (8 markets), and Figure 1(b) for CI-quality treatment (9 markets), the most frequent strategy over time is the risk dominant strategy LA. Initially, the alternative, payoff dominant equilibrium strategy (HA in the CI-quality treatment, and LB in the CI-price treatment) is observed in the repeated game as well, and nearly as frequently as the risk dominant strategy LA (and only when it is an equilibrium strategy for the given parameterization). These strategies, however, disappear over time. This supports the perspective that subjects face initially a coordination problem, and resolve the tradeoff between the risk and payoff dominant equilibrium in favor of the risk dominant one. We find little evidence for the collusive strategy HB.
These observations can be also made on the individual market level, see Table 4. Here, we list the frequency of strategies over the 15 periods per market, and well as the most frequent strategy. The table supports that the coordination problem in the Complete information treatment is resolved mostly in favor of the risk dominant equilibrium (LA, LA). Collusion (strategy HB) is either fully absent, or prevails strongly. Indeed, we observe two markets, one in each Complete information treatment, that end up in nearly full collusion. Given the small number of such collusive observations, it is difficult to speculate on the reasons for the collusion in these two, and not in the remaining markets. However, collusion is less likely market outcome than the use of the risk dominant strategy LA.
We will now compare behavior under complete information, with known characteristic of the demand, to the strategies chosen under incomplete information, when preferences of the consumers are unknown to the insurers. To control for insurers’ beliefs, we asked them in each round to reveal which product they expect to have higher demand when both available, HA or LB. In 175 of the 180 cases (97%), the insurers expected that half or more consumers would choose product HA rather than LB. In fact, these beliefs are correct, as we can deduce from consumer responses. In each round of the Incomplete information treatment, we also asked consumers to state whether they would choose HA or LB if facing such tradeoff. With only one exception (one round in one market), in all rounds and markets we observed that more than 50% of the consumers prefer HA over LB.
This information can be used to relate strategies in the Incomplete information treatment to the belief-relevant Complete information treatment that has demand characteristics corresponding to the insurers’ beliefs under incomplete information. We therefore compare behavior in the Incomplete information treatment to the behavior in the CI-quality treatment. These two treatments have in common that more than half of the consumers prefers HA over LB; and that each of the insurers knows (in the CI-quality treatment) or believes (in Incomplete information treatment) that this is the case. The two treatments, therefore, differ only in whether the information on consumer preferences is commonly shared by the two insurers (in the CI-quality treatment), or not (in the Incomplete information treatment); that is, whether the identity of the payoff dominant equilibrium is common knowledge among the insurers (in the CI-quality treatment) or not (in the Incomplete information treatment).
The Incomplete information treatment strategy choices are presented in Figure 1(c). In contrast to the Complete information treatments, it is no longer the case that the risk dominant LA strategy prevails over time. In-
Table 3. Sessions.



Figure 1. Evolution of strategy choices over time per treatment. (a) CI-price treatment (h = 0); (b) CI-quality treatment (h = 1); (c) II treatment (h unknown).
Table 4. Strategies frequencies per treatment and group.
stead, it co-exists with strategy HA. Indeed, as Table 4 reveals, strategy HA is also the most frequent strategy in four out of six markets in the Incomplete information treatment.
The difference in the play of risk and payoff dominant strategies between the Incomplete information treatment and the belief-corresponding Complete information treatment CI-quality is remarkable. While in the complete information case, the competition mostly results in the risk dominant equilibrium, the payoff dominant one survives under incomplete information and is at least as frequent, if not more.
To address how uncertainty about consumers’ preferences affects the strategic behavior of insurers, we now study how insurers react to the observed strategies from the previous round. In both treatments, insurers face multiplicity of equilibria, and strategic uncertainty with respect to the choices of their rivals. After each round they learn the strategy chosen by the other insurer. When the observed strategy is an equilibrium strategy of the game, myopic best response behavior predicts to respond with the same strategy in the next period. The game, however, remains a coordination problem in each round. Players, especially at the start of the game, might try to escape coordinating on the payoff dominated equilibrium (LA, LA). But, this is difficult as observing that the other subject chose the safe strategy LA might be interpreted as a signal of distrust, and discourage the efforts to play another strategy―even if potentially resulting in higher payoffs.
We find that subjects respond differently to observing the risk dominant strategy LA in the previous period when they face strategic uncertainty only (as in the Complete information treatment) and when they also face fundamental uncertainty on top of the strategic uncertainty (as in the Incomplete information treatment). The fundamental uncertainty implies that the identity of the payoff dominant equilibrium is unknown for the insurer. Moreover, the insurer also faces uncertainty about what strategy the other player considers to the payoff dominant equilibrium strategy. Overall, it might seem that this added uncertainty will complicate the coordination on payoff dominant equilibrium. However, we have seen that this is not the case. What explains that this increased uncertainty allows players to coordinate on the payoff dominant equilibrium?
In Table 5 we show transition matrices―the probability of choosing a certain strategy in period t, depending on the strategy observed on the part of the competitor in period t − 1, split up into the first and second half of the experiment. Observing the risk dominant strategy LA in both Complete information treatments (panel (a) and (b)) mainly results in using strategy LA as well. This is the case even in the first half of the experiment, where subjects still might attempt to collude or to coordinate on the alternative payoff dominant equilibrium. In contrast, observations of the risk dominant strategy LA do not trigger the same response in the first half of the experiment in the Incomplete information treatment. Players seem to give the benefit of the doubt to their competitors in such case, and keep trying to coordinate on one of the other strategies. In the second half of the experiment, however, the situation is different, and observing strategy LA results in choosing LA as well. This is in line with subjects using the first half of the experiment to teach the other player to play the payoff dominant equilibrium, to escape the trap of the risk dominant equilibrium (LA, LA).
The role of the information about consumer preferences as identified by casual browsing of the strategy frequencies in individual markets (Table 4) and by the transition matrices (Table 5) will now be supported in a regression analysis. We analyze data from the Incomplete information treatment and the CI-quality treatment. In these two treatments, the fraction of consumers that prefer HA over LB either objectively satisfies h > 2/5 (in CI-quality treatment), or insurer subjects believe that this is the case (in Incomplete information treatment).
We estimate a multinomial logit model, where the dependent variable is the insurer’s strategy LA, LB, HA or HB (see Table 6). The change in probability of each of the four available strategies between the Complete (CI- quality) and the Incomplete information treatment supports the effects we described so far. The regression coefficients in the model contrasting the use of the LA strategy against strategy LB and HA are statistically significant. To assess their actual relevance for estimated changes in behavior, we evaluate the estimated probability change of each strategy use in our non-linear model. After the first half of the repeated game, the use of strategy LA is estimated to increase significantly by about 30% when switching from the Incomplete information treatment to the CI-quality treatment, accompanied mostly by a decline in observations of the strategy HA.
To summarize, we have observed in the Complete information treatments that the demand characteristics affect the strategies chosen by the insurers in the short run, with insurers choosing strategies revealing the tradeoff between the risk dominant strategy LA, and the relevant payoff dominant strategy, either HA (in CI-quality, when h = 1), or LB (in CI-price, when h = 0). In the long run, the risk dominant strategy LA prevails in both Complete information treatments.
However, when information about the preferences of the consumers is not commonly known to the insurers, a different situation arises. We observe that fundamental uncertainty―next to strategic uncertainty―helps insurers to coordinate on the payoff dominant equilibrium much more frequently than on the risk dominant one. Indeed, in the last period of the Incomplete information treatment, the payoff dominant HA strategy is twice as frequent as the risk dominant LA strategy.
4. Discussion
In our introduction, we have elaborated that subjects within the same class of stag hunt games sometimes coordinate on the risk dominant equilibrium, and other times on the payoff dominant equilibrium. It has been suggested that the costs of mistaken coordination affect the ability of players to sustain the payoff dominant equilibrium, and this highlights the role of the dynamics of the play, and inductive reasoning of subject next to deductive reasoning.
In our study, subjects interact under incomplete information, in such a way that the risk dominant equilibrium is always the same strategy combination, but the identity of the payoff dominant equilibrium depends on the state of the world. Consequently, the intentions underlying the choice of the risk dominant equilibrium strategy by the other player are less clear under incomplete information. Not playing the payoff dominant equilibrium strategy may be due to the player’s decision not trusting the other player. At the same time, it could be also due to the uncertainty about the state of the world, and the identity of the payoff dominant equilibrium. This latter interpretation of miscoordination events under incomplete information might motivate players to keep signaling
Table 5. Transition matrices. (a) Complete information: CI-price treatment; (b) Complete information: CI-quality treatment; (c) Incomplete information treatment.
Table 6. Multinomial logit regression explaining the choice of the strategy LA, LB, HA, or HB with strategy LA as the base category.
aThe top entries are multinomial logit coefficients. Standard errors are in parentheses; bVariable CI = 1 if CI-quality treatment, CI = 0 if Incomplete information treatment; cEstimated discrete probability change from CI = 0 to CI = 1, at Period = 8 (results insensitive to Period choice). ***p < 0.01; **p < 0.05; *p < 0.10 (two-tailed tests).
their willingness to play the payoff dominant equilibrium, and at the same time “teaching” the other player what strategy they believe to be the payoff dominant one.
This mechanism of uncertainty affecting coordination behavior thus differs from uncertainty so far studied in coordination games. Prominently, this would be studies implementing global games [24] where deductive reasoning of players, and iterative elimination of strictly dominated strategies is studied in the light of the theoretically proposed the impact of noise on the selection of the risk dominant equilibrium. In our paper, there is no uncertainty about what action is the risk dominant equilibrium, and uncertainty prevails only about which of the two alternative strategies is the payoff dominant equilibrium strategy.
The authors in [25] investigate theoretically a game with one risk dominant equilibrium and multiple payoff dominant equilibria. They show that the multiplicity of payoff dominant equilibria can increase the likelihood of coordinating on the risk dominant equilibrium. In their model, however, the payoff dominant equilibria co-exist, amplifying the coordination problems. In our model, the identity of the payoff dominant equilibrium changes, depending on the demand characteristics, but there is always only one payoff dominant equilibrium.
Another illustration of uncertainty supporting the selection of the payoff dominant equilibrium is given by [26] . In their experiment, subjects play stag-hunt games with perturbed payoffs and changing labels, in a random matching protocol. Each game represents a coordination problem, but the payoff and risk dominance changes slightly with the perturbations, as well as the label of the payoff/risk dominant equilibrium. Under such volatile environment, although initially the occurrence of payoff dominant strategy lies outside the basin of attraction of this equilibrium, the payoff dominant equilibrium over time unambiguously prevails. Several explanations are possible. For example, noise in the action labeling might motivate subjects to select the cognitively less demanding, possibly therefore more salient behavioral rule, one of choosing the action that yields the highest payoff. Alternatively, however, subjects might be less punishing in responding to the risk dominant actions by their co-players in such a volatile environment. This last explanation shares with our work the aspect of a more reluctant response to the risk dominant action, when it is an unclear signal of a lack of trust.
Finally, a study relevant to ours is [16] . The authors consider not only backwards looking but also forward looking players, studying teaching in stag hunt games. They provide evidence that some subjects, instead of merely reacting to observed past behavior of others, adopt active forward looking strategies and attempt to teach co-players to escape the coordination problems.
5. Conclusions
Western countries face increasing health care costs, reduced access to health care services, lower quality of these services, and less innovation in the health sector. This prompted several of them, including the Netherlands, Germany and the US to initiate health care reforms introducing features of regulated competition. The goal of these reforms was to increase the economic efficiency of the health care sector while keeping the welfare of the consumers in mind [27] [28] .
A prominent example of the implementation of regulated competition is the Dutch health insurance market, where as of 2006 each consumer is obliged to purchase basic health insurance, the content of which is stipulated by law [1] [29] [30] . Insurers compete on price and quality of their delivered products trying to attract additional consumers. However, due to incomplete information about consumer preferences, insurance companies face difficulties competing in this regulated market.
In this paper, we focus on the coordination problem that arises from simultaneous price and quality setting on a market with regulated competition. In the coordination game we design, the set of equilibria depends on the parameter characterizing the demand with respect to the consumers’ willingness to pay for high quality. However, we also observe that the most desirable outcome, with low prices and high quality for the consumers, is an equilibrium of the game independent of the consumer preferences. We study this game experimentally under two experimental treatments: in the Complete information treatment we simulate the demand and publicly inform the insurer players about the demand characteristics. This information is thus common among the insurers. In the Incomplete information treatment, however, real subjects play the role of consumers, and the information about their preferences is not known to the insurer players. And despite being able to form beliefs about the consumer preferences, insurers still face uncertainty about the beliefs held by their rivals in this treatment.
The main finding of this paper is that insurers use a different strategy most frequently when the coordination problem is played under incomplete information and when it is played under complete information. In particular, they coordinate more frequently on the payoff dominant equilibrium under incomplete information. The lack of commonly shared information on consumers’ preferences, a rather realistic assumption, generates thus lower consumer welfare than when this information is available. This is reflected in more frequent play of a strategy using high prices (strategy HA).
Our experiment suggests that information on consumers’ preferences might crucially affect the dynamics in the market and it should be addressed when innovating health insurance markets in the spirit of regulated competition. Creating awareness of consumer preferences using public means of communication, and generating common knowledge of these preferences removes fundamental uncertainty from the decision problem of the insurers. Our experiments suggest that this supports more competitive market outcomes in the price/quality setting coordination problem the insurers face.
The implications for the literature on coordination games are equally interesting. Adding to the awareness that miscoordination costs play a role, our results propose that the intentions behind the miscoordination affect how irreparable the impact of observing the risk dominant strategy is while attempting to coordinate on the payoff dominant equilibrium. In our study, the Incomplete information treatment allows interpreting the risk dominant strategy observations as a consequence of fundamental uncertainty, rather than lack of trust. Insurers then persist longer in trying to achieve payoff dominance, and are more successful in achieving this goal.
Acknowledgements
Funding for this research was provided by the Department of Economics, Radboud University Nijmegen, the Netherlands.
References
- Van Beest, F., Lako, C.J. and Sent, E.M. (2012) Health Insurance and Switching Behavior: Evidence from the Netherlands. Health, 4, 811-820. http://dx.doi.org/10.4236/health.2012.410125
- Diamond, D.W. and Dybvig, P.H. (1983) Bank Runs, Deposit Insurance, and Liquidity. The Journal of Political Economy, 91, 401-419. http://dx.doi.org/10.1086/261155
- Obstfeld, M. (1996) Models of Currency Crises with Self-Fulfilling Features. European Economic Review, 40, 1037- 1047. http://dx.doi.org/10.1016/0014-2921(95)00111-5
- Brandts J. and Cooper, D.J. (2006) A Change Would Do You Good... An Experimental Study on How to Overcome Coordination Failure in Organizations. American Economic Review, 96, 669-693. http://dx.doi.org/10.1257/aer.96.3.669
- Enthoven, A.C. (1993) The History and Principles of Managed Competition. Health Affairs, 12, 24-48. http://dx.doi.org/10.1377/hlthaff.12.suppl_1.24
- Harsanyi, J.C. and Selten, R. (1988) A General Theory of Equilibrium Selection in Games. MIT Press, Cambridge.
- Carlsson, H., and van Damme, E. (1993) Global Games and Equilibrium Selection. Econometrica, 61, 989-1018. http://dx.doi.org/10.2307/2951491
- Straub, P.G. (1995) Risk Dominance and Coordination Failures in Static Games. Quarterly Review of Economics and Finance, 35, 339-363. http://dx.doi.org/10.1016/1062-9769(95)90048-9
- Rydval, O. and Ortmann, A. (2005) Loss Avoidance as Selection Principle: Evidence from Simple Stag-Hunt Games. Economics Letters, 88, 101-107. http://dx.doi.org/10.1016/j.econlet.2004.12.027
- Dubois, D., Willinger, M. and Van Nguyen, P. (2012) Optimization Incentive and Relative Riskiness in Experimental Stag-Hunt Games. International Journal of Game Theory, 41, 369-380. http://dx.doi.org/10.1007/s00182-011-0290-x
- Battalio, R., Samuelson, L. and Van Huyck, J. (2001) Optimization Incentives and Coordination Failure in Laboratory Stag Hunt Games. Econometrica, 69, 749-764. http://dx.doi.org/10.1111/1468-0262.00212
- Feltovich, N., Iwasaki, A. and Oda, S.H. (2011) Payoff Levels, Loss Avoidance, and Equilibrium Selection in Games with Multiple Equilibria: An Experimental Study. Economic Inquiry, 50, 932-952. http://dx.doi.org/10.1111/j.1465-7295.2011.00406.x
- Goree, J.K. and Holt, C.A. (2005) An Experimental Study of Costly Coordination. Games and Economic Behavior, 51, 349-364. http://dx.doi.org/10.1016/j.geb.2004.08.006
- Van Huyck, J.B., Battalio, R.C. and Rankin, F.W. (2007) Evidence on Learning in Coordination Games. Experimental Economics, 10, 205-220. http://dx.doi.org/10.1007/s10683-007-9175-z
- Schmidt, D., Shupp, R., Walker, J.M. and Ostrom, E. (2003) Playing Safe in Coordination Games: The Roles of Risk Dominance, Payoff Dominance, and History of Play. Games and Economic Behavior, 42, 281-299. http://dx.doi.org/10.1016/S0899-8256(02)00552-3
- Hyndman, K., Terracol, A. and Vaksmann, J. (2009) Learning and Sophistication in Coordination Games. Experimental Economics, 12, 450-472. http://dx.doi.org/10.1007/s10683-009-9223-y
- Atherly, A., Dowd, B. and Feldman, R. (2004) The Effect of Benefits, Premiums, and Health Risk on Health Plan Choice in the Medicare Program. Health Services Research, 39, 847-864. http://dx.doi.org/10.1111/j.1475-6773.2004.00261.x
- Abraham, J.M., Feldman, R., Carlin, C. and Christianson, J. (2006) The Effect of Quality Information on Consumer Health Plan Switching: Evidence from the Buyers Health Care Action Group. Journal of Health Economics, 25, 762- 781. http://dx.doi.org/10.1016/j.jhealeco.2005.11.004
- Beaulieu, N.D. (2002) Quality Information and Consumer Health Plan Choices. Journal of Health Economics, 21, 43-63. http://dx.doi.org/10.1016/S0167-6296(01)00126-6
- Hendriks, M., de Jong, J., van Brink-Muinen, A. and Groenewegen, P. (2010) The Intention to Switch Health Insurer and Actual Switching Behaviour: Are There Differences between Groups of People? Health Expectations, 13, 195-207. http://dx.doi.org/10.1111/j.1369-7625.2009.00583.x
- Van Beest, F., Lako, C., Vyrastekova, J. and Sent, E.M. (2008) Veranderen van zorgverzekeraar. Economisch Statistische Berichten, 93, 518-521.
- Basov, S. (2004) Equilibrium Selection in Coordination Games: Why Do Dominated Strategies Matter? Economics Bulletin, 3, 1-3.
- Fischbacher, U. (2007) z-Tree: Zurich Toolbox for Ready-Made Economic Experiments. Experimental Economics, 10, 171-178. http://dx.doi.org/10.1007/s10683-006-9159-4
- Cabrales, A., Nagel, R. and Armenter, R. (2007) Equilibrium Selection through Incomplete Information in Coordination Games: An Experimental Study. Experimental Economics, 10, 221-234. http://dx.doi.org/10.1007/s10683-007-9183-z
- Golman, R. and Page, S.E. (2010) Individual and Cultural Learning in Stag Hunt Games with Multiple Actions. Journal of Economic Behavior & Organization, 73, 359-376. http://dx.doi.org/10.1016/j.jebo.2009.11.005
- Rankin, F.W., Van Huyck, J.B. and Battalio, R.C. (2000) Strategic Similarity and Emergent Conventions: Evidence from Similar Stag Hunt Games. Games and Economic Behavior, 32, 315-337. http://dx.doi.org/10.1006/game.1999.0711
- Dormont, B., Geoffard, P.Y. and Lamiraud, K. (2009) The Influence of Supplementary Health Insurance on Switching Behaviour: Evidence from Swiss Data. Health Economics, 18, 1339-1356. http://dx.doi.org/10.1002/hec.1441
- Wendt, C., Agartan, T.I. and Kaminska, M.E. (2013) Social Health Insurance without Corporate Actors: Changes in Self-Regulation in Germany, Poland and Turkey. Social Science & Medicine, 86, 88-95. http://dx.doi.org/10.1016/j.socscimed.2013.02.044
- Rosenau, P. and Lako, C.J. (2008) The New Dutch Health Insurance System. Journal of Health Politics, Policy and Law, 33, 1031-1055.
- Rosenau, P. and Lako, C.J. (2008) Health Insurance Experiments in the Netherlands and Switzerland: A Rejoinder with Updates. Journal of Health Politics, Policy and Law, 33, 1073-1077. http://dx.doi.org/10.1215/03616878-2008-037
NOTES
1Previous studies evaluating the working and success of these institutional innovations mainly focused on the role of consumers’ choices [17] - [21] . Our experiments are designed to study whether information about consumers’ preferences for increasing quality of the insurance plans has an impact on market outcomes.
2The safer, risk dominant strategy―in a coordination game is an equilibrium strategy that maximizes the expected payoff of an insurer who is uncertain which of the two equilibrium strategies the competitor plays, and hence assumes that each of them is played with the same probability.
3In reference [22] , it is shown that the presence of a strictly dominated strategy in a game might affect the selection between risk and payoff dominant equilibrium. This happens, however, if the payoff of the strictly dominated strategy differs when played against the risk dominant equilibrium strategy and when played against the payoff dominant equilibrium strategy. In our game, however, is this payoff equal to zero against all alternative strategies. This validates the perspective that players, either by introspection or by learning, will eliminate the strictly dominated strategies and perceive a coordination problem between choosing LA and choosing the alternative strategy, ether HA (if h > 2/5) or LB (if h < 2/5).





