Engineering
Vol.09 No.05(2017), Article ID:76639,16 pages
10.4236/eng.2017.95023
A Study of Temperature and Aging Effects on Eigenfrequencies of Concrete Bridges for Health Monitoring
Viet Ha Nguyen1, Jean Mahowald1, Sebastian Schommer1, Stefan Maas1, Arno Zuerbes2
1Faculty of Science, Technology and Communication, University of Luxembourg, Luxembourg City, Luxembourg
2Technische Hochschule, Bingen, Germany

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 15, 2017; Accepted: May 24, 2017; Published: May 27, 2017
ABSTRACT
This paper discusses the influence of environmental factors and of normal material aging on the eigenfrequencies of concrete bridges based on monitoring data registered during 4 years of a specific bridge. It is a new composite steel-concrete bridge built in 2006 in Luxembourg. The measurements are analyzed and compared to literature data. The final objective is the use of real monitored eigenfrequencies for structural health monitoring and damage detection based on identification of stiffness losses in practical applications. Therefore, it is very important to identify and compensate for outdoor influences namely temperature, excitation force level and normal aging effects, like creep and shrinkage of concrete and their impact on material properties. The present paper aims at describing these effects in order to separate them from damage effects. It is shown that temperature change rates and temperature gradients within the bridge have an influence on the eigenfrequencies. Hence the key idea for assessment from the full database is to select only measurements with small temperature differences and slow temperature change rates.
Keywords:
Damage Detection, Long-Term Monitoring, Eigenfrequency, Aging, Temperature

1. Introduction
Structural Health Monitoring has been developed a lot in the last years to assure safe and reliable exploitation as well as economical maintenance of structures. The monitoring of a system is often carried out by tracking static or dynamic characteristics during its life and by comparing those characteristics to the healthy reference state. However, some significant difficulties arise from environmental and operational influences. This paper discusses the influence of temperature and aging effects on the eigenfrequencies, which are in the same order of magnitude or may even be more important than the variation provoked by severe damage. Hence these sources of irritation may cause false alarm or on the contrary hide real damage. Some researchers tried to remove temperature effects before performing damage detection by mathematical transformations [1] [2] [3] . Nonetheless real bridges sustain numerous environmental effects like temperature variation, wind, humidity, traffic, changing boundary condition and aging of concrete and asphalt. Thence, an investigation of these effects is essential to better understand the behavior of the structure and to work on efficient compensation algorithms.
To study the temperature effect on dynamic characteristics, different concrete bridges were monitored for years within a large band of temperature [3] - [8] . The representation of eigenfrequency versus temperature shows often a quite linear relation, but in some cases also a strong nonlinear form, before all when freezing takes place [5] [9] [10] . The results from diverse researches may be dissimilar and are summarized in chapter 3 and show also that the scatter and the slope of frequency-temperature plots may vary largely between different bridges. As an example, the eigenfrequencies of a new composite steel-concrete bridge in Luxembourg were registered from 2007 to 2010. The authors try to analyze at least some of the parameters that influence this scatter and can reduce it by judiciously limiting temperatures, their differences and their change rates. This is an originality of the present paper which is of high importance for any practical application on site, especially when the number of studies on dynamic parameters with temperature problems in real bridges is still really limited.
Another aspect examined in this work is the aging of concrete. While some studies from literature showed that the stiffness of concrete bridge was reduced over time [7] [8] [11] , others authors detected an increase [3] [4] or attacked the issue numerically [12] . Our observations of the above-mentioned sample bridge and the measurement of its first 3 eigenfrequencies show in general a decrease over the years. Hence there is the necessity of a regular individual control and tracking to separate normal aging/temperature effects from damage.
2. Description of Structure
The investigated bridge was built in 2006 and is located in Useldange (Luxembourg) and crosses the creek Attert. It is a composite two-span bridge with a total length of 37.3 m divided into two fields of 23.9 m and 13.4 m span lengths as sketched in Figure 1. The upper plate has a thickness of 25 cm and is made of concrete C45/55. This concrete plate is held by four main longitudinal steel girders of S355 with heights ranging from 0.5 m to 1.3 m following the bending moment. Two steel longitudinal girders are connected to each other with transversal girders every 4 m. The asphalt layer has a thickness of 25 cm, which is relatively heavy compared to common thickness varying from 8 cm to 10 cm [13] . It should also be highlighted that this bridge has two fixed (or let us better say more or less clamped) polymer supports: one at the south side (axis C) and one at the column in the middle (axis B). A sliding support is located at the north abutment (axis A).
The time data were recorded using 8 accelerometers and by 7 temperature sensors installed on the bridge as shown in Figure 1. The acceleration data were captured daily from 2:00 to 22:00 h with a sample rate of 200 Hz. The installation of the transducers and the acquisition system took place in 2006 and the monitoring began in January 2007. Figure 2 shows for instance acceleration data, where clear traffic periods can be recognized. For this small bridge, modal identification was performed by the excitation of road traffic. The acceleration data were scanned using a rolling window of constant width to search for dynamic events, when the acceleration passed an arbitrarily threshold of 0.0015 m/s2. As reported in [13] for this bridge, a whole time signal due to a vehicle
Figure 1. Positions of the temperature transducers and the accelerometers on the bridge for monitoring [13] .
Figure 2. Example of time data from one accelerometer defining traffic and non-traffic periods, shown between 15h03 and 15h07 of a day.
crossing has a total length of about 13 seconds. The vehicle is typically for 4 seconds on the bridge. In order to avoid the effect of additional unknown mass, the signals were analyzed after cutting these first 4 seconds, assuming that the vehicle then has left the bridge.
For each dynamic event, Stochastic Subspace Identification (SSI) [14] is performed to identify the modal parameters. The number of blocks used for Hankel matrices is 10 that appears an adequate number. Modal parameters were identified by basing on a stabilization diagram [5] to exclude noisy numerical modes and to choose stabilized physical modes.
To shorten the data size, the values of temperature were simply averaged for every period of 15 minutes. Each traffic event was analyzed and the eigenfrequencies were calculated. Then they were averaged for a 15-minute time period and written in the stored data matrix.
3. Temperature Effects on Eigenfrequencies
The weather influence on the structure is clearly shown by the contrast between winter and summer. Figure 3 presents the daily temperatures in June 2008 as well the corresponding first eigenfrequency around 4.1 Hz, while Figure 4 shows the results in December 2008 with an eigenfrequency of approximatively 4.8 Hz.
Figure 3. Data in June 2008.
Figure 4. Data in winter 2008.
Figure 3 reveals clearly the important difference of temperature between day and night (up to 10 K) and between steel and concrete (up to 6 K). Figure 4 presents cloudy winter days, where this difference nearly disappears. Hence the decrease of temperature in winter induced an important increase of eigenfrequency of at least 14% for this bridge. It should be noted that serious damage affects the eigenfrequencies in the same order of magnitude [5] [10] [13] [15] .
In order to find a relation between the eigenfrequencies and temperatures, corresponding plots were prepared. Figure 5(a) shows for instance the first



Figure 5. Plot between the first eigenfrequency versus the temperature from the structures.
eigenfrequency versus a temperature measured in the concrete by sensor T2 (for the positions refer to Figure 1). As expected, a clear tendency of decrease with temperature is shown for this eigenfrequency. The relation is quite linear and hence it may be approximated by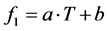 , as indicated by the bold regression line. The standard deviation σ was calculated with respect to the regression line and not with respect to a constant mean value. The bandwidth of the scatter diagram is indicated by ±3 times the standard deviation σ.
, as indicated by the bold regression line. The standard deviation σ was calculated with respect to the regression line and not with respect to a constant mean value. The bandwidth of the scatter diagram is indicated by ±3 times the standard deviation σ.
For comparison, some similar plots from the Z24-bridge (Switzerland) [5] and the Dowling Hall Footbridge (USA) [16] are juxtaposed in Figure 5(b) and Figure 5(c) respectively. For the Z24-bridge, a linear relation between the first eigenfrequency and the surface temperature may be approximated in the range between 0˚C and 40˚C. For the Dowling Hall Footbridge, a linear relation may be also matched in the positive range of temperature. However, the plots reveal clearly that neither the bandwidth ±3σ nor the slope “a” is the same for every bridge. The bandwidth ±3σ from the measured scatter diagram is approximately 13% for the first bridge, about 2.5% for the second and about 1.7% for the third. The slope “a” is approximately 7‰ per ˚C for the first bridge and only 1‰ per ˚C for the second and even about 0.64‰ per ˚C for the third. Hence these quantities are highly different for individual bridges depending on relevant characteristics, namely their type of construction, their supports and their asphalt layer. No standard value can be given for an individual bridge, but has to be measured a-posteriori. In Figure 5(b) and Figure 5(c), another interesting effect may be seen on some bridges at temperatures below 0˚C, where the stiffness of the structure and/or the bearing conditions change significantly probably due to freezing. Some other examples of monitored bridges may be found for instance in [6] [9] [10] .
A bandwidth ±3σ = ±0.29 Hz for this bridge in Useldange means for one specific temperature, an uncertainty of 0.58 Hz, which is equal to 0.58 Hz/4.5 Hz ≈ 13% and hence an extremely high value. This bandwidth reflects measurement uncertainties and non-linear effects of the structure and the bearings. Why it is so important for structural health monitoring to separate damage influence from temperature, aging and nonlinear effects. It is evident that temperatures and also their gradients play an important role, while damage effects can be excluded here for this new bridge. Therefore, the eigenfrequencies are now analyzed for different temperature gradients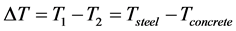 . A more detailed description of ΔT and its relation on frequency modulation is given by Mahowald et al. 2014 [17] . One can recognize in Figure 6 that the slope a is approximately the same for any regression line for different ΔT-intervals; whereas the offset value b (eigenfrequency at 0˚C) is lower for high temperature gradient intervals ΔT.
. A more detailed description of ΔT and its relation on frequency modulation is given by Mahowald et al. 2014 [17] . One can recognize in Figure 6 that the slope a is approximately the same for any regression line for different ΔT-intervals; whereas the offset value b (eigenfrequency at 0˚C) is lower for high temperature gradient intervals ΔT.
Figure 7 investigates the value b (eigenfrequency at 0˚C) for the years 2007 to 2010. These b-values clearly depend on ΔT, but not on age. The lowest values were detected in 2009 and the highest in 2010, while 2007 and 2008 lead to values in between.
Figure 6. First eigenfrequency versus the concrete temperature T2 of the bridge in Useldange for the year 2008 with the tracing of regression lines for different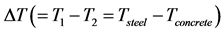 .
.
Figure 7. Synthesis of b-offset values (eigenfrequency at 0˚C) from f1 for 4 years: 2007-2010.
The relation of the higher eigenfrequencies and the temperature is also considered and are presented in Figure 8 and Figure 9 for the year 2008. The regression lines appear again quite parallel and their order according to different intervals of ∆T (values b) agrees with the results from the first eigenfrequency. However, the bandwidth of the scatter diagrams is larger for higher frequencies, probably due to the fact that the traffic excites more the lower frequencies, leading to a better observability for these.
One may summarize that the characteristic eigenfrequencies versus temperature and even temperature gradient of an individual bridge has to be known prior to damage assessment in order to separate temperature from damage effects. The larger the bandwidth of the scatter diagram, the more difficult is damage detection because it adds uncertainty to any identified eigenfrequency. As already stated severe damage of concrete bridges causes eigenfrequency reduction of about 10% ( [13] [15] [18] ). Let us consider, for instance this Useldange-bridge
Figure 8. Second eigenfrequency versus the concrete temperature T2 of the bridge in Useldange for the year 2008 with the tracing of regression lines for different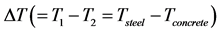 .
.
Figure 9. Third eigenfrequency versus the concrete temperature T2 of the bridge in Useldange for the year 2008 with the tracing of regression lines for different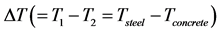 .
.
that the slope-value a is 7‰ per ˚C while a temperature change compared to the reference measurements of 20˚C or even 30˚C, plus an uncertainty bandwidth of 6.5%, it can be observed easily 20% change of eigenfrequency without damage. Hence a compensation for structural health monitoring becomes mandatory that is detailed in Section 5.
The bridge was monitored from 2007 to 2010 and the identified slope values a are reported in Figure 10.
It can be seen in Figure 10 that the slope-values for f1 and f2 are quite stable while for f3, the scatter is larger due to its lower observability.
The offset values b or the eigenfrequencies at 0˚C are shown in Figure 11 for different intervals of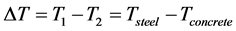 . The figure reveals two facets: the evolution of b with respect ΔT and age. Firstly, the offset b shows a clear dependency on ΔT for every eigenfrequency. In each year, the band
. The figure reveals two facets: the evolution of b with respect ΔT and age. Firstly, the offset b shows a clear dependency on ΔT for every eigenfrequency. In each year, the band
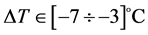 is often in summers (hot) that eigenfrequencies are higher. On the other hand, the band
is often in summers (hot) that eigenfrequencies are higher. On the other hand, the band 
Secondly, by comparing the four years in each band ΔT, in general a decrease with age is observed from f2 and f3. However from f1, a contrary is noticed since the b values are surpassing in the last year―2010 and an increase by time in the last band

Figure 10. Evolution of the slope values a over 4 years, for different interval of ΔT.



Figure 11. Ordinate: measured offset b in Hz (eigenfrequency at 0˚C), abscise: different intervals of ΔT, for the years 2007 to 2010.
of the year 2007 was the warmest among the examined years. On the other hand, always in Figure 11(a), the offset values of 2010 are generally more important than the other years with negative bands ΔT that belong much to spring and summer. This effect may due to the fact that the temperature in spring 2010 was lower than the other 3 years. Nevertheless, by relying upon the absolute temperature, it is necessary to mention that only f1 shows this sensitiveness, while the evolution of f2 and f3 presents quite consistent with age.
4. Aging of Concrete
It should be recalled that published results about long-term monitoring of eigenfrequencies in concrete structures are relatively rare and the observations do not show all the same tendency. The reduction of eigenfrequencies relates to decrease of structural stiffness evoked by the ageing, i.e. by micro-cracking and cracking and the creep of the concrete. The reduction of eigenfrequencies relates to a decrease of structural stiffness, by reduction of the apparent Young’s modulus of this composite material. This phenomenon is coherent with observations cited subsequently. The Jamboree Bridge (USA) [8] was opened to traffic in 1998. Over the 5-year monitoring period, a statistical analysis resulted in 5% decrease of the first eigenfrequency and 2% decrease of the stiffness of the bridge deck. The West Street On-Ramp concrete bridge was built in 2001 and monitored from 2002 to 2010 [7] . It showed small, but continuous reduction of eigenfrequencies of 7% - 8% for the first and third modes and 5% for the second mode during 8 years of monitoring. It was proven that this reduction did not relate to six earthquake events registered during the monitoring period. A quite copious picture on long-term monitoring of concrete structures in Eastern Europe was drawn by Pirner et al. 2009 [11] . The paper describes 8 concrete constructions (bridges, chimney, high building) where 7 structures showed ascertained drops of fundamental natural frequency over time. Only the prestressed Brno motor-way bridge did not show any change in frequency after 32 years of service. However, the influence of temperature variation was not studied for these structures.
However, based on numerical simulations, Au Francis et al. 2012 [12] proved that eigenfrequencies of concrete bridges may increase between 28 up to 300 days, before they stabilize due to the setting of cement. But also increase of frequencies was observed at the Infante D. Henrique Bridge in Portugal [4] which was opened to traffic in 2004 and monitored from 2007 to 2012. Frequencies and temperatures were averaged every year, but no direct relation was found. For this bridge, the first eigenfrequency did not show a clear tendency, whereas all the other modes showed an increase in frequency.
Summarily, the literature review of concrete structures given above shows several cases that eigenfrequencies reduced by time. However, few observations revealed unchanged or increased tendency.
In the present work, simultaneously with long-term monitoring, the authors attempt to consider the dependency between eigenfrequency and temperature as well as temperature gradient, as illustrated by Figures 6-12. The relative variation of the b-value (the eigenfrequencies at


5. Reduction of the Scatter by Limitation of Temperature Change Rates
As explained in section 3, the bandwidth of the scatter ±3σ around the regression line in the diagram eigenfrequency versus concrete temperature is very high for this specific bridge. It was shown that the temperature gradient




Figure 12. Relative change of the eigenfrequencies at 0˚C in 4 years for different intervals of ΔT.
Let us return to the scatter diagram in Figure 6 for f1 in 2008 that considers five different intervals of gradients ΔT with different widths. All sampled data are presented according to their gradient ΔT and shown in Figure 13, which are of course not equally distributed as the number of samples in different intervals ΔT is not equivalent. For instance, if data appear more frequent in a certain interval then statistical parameters of this interval are more confident.
Additionally, the standard variations σ with respect to the linear regression lines in Figure 6 (and not with respect to constant values) were calculated for each interval. The interval of 
Table 1. Summary of eigenfrequency reduction of structures.
Figure 13. Identified f1 in 2008 versus temperature gradients ∆T with number of samples and standard deviation σ with respect to the linear regression line per interval.
ΔT > 1.5˚C should not be considered because the number of samples in these intervals is quite small. Then the absolute concrete temperatures between 0˚C and 15˚C were then selected, because freezing effects in winter and high radiation effects in summer were considered as extreme scenarios, where measurements should be avoided. On cloudy days, in the medium temperature range, these moderate conditions should be found that should lead to reliable data. Therefore a limitation of variation speed for T and ΔT is proposed by imposing


Figure 14 presents an example of the selected data. For the first eigenfrequency, the initial data in Figure 6 lead to a half bandwidth of 3σ = 0.291. Now if only data 

Figure 15(a) shows the half bandwidths 3σ graphically for the first eigenfrequency. The first value for any year presents a half bandwidth of the full data. The second column corresponds to the data belonging to 

reduction of the variation speed, i.e. the slopes 

Similar calculations were carried out for the half bandwidth 3σ for the second and the third eigenfrequencies, which are reported in Figure 15(b) and Figure 15(c). They reveal clearly a reduction of the standard-deviation compared to the
full data. The limitation of the slopes 

Figure 14. First eigenfrequency versus the concrete temperature T2 in 2008― The green “o” are all data






Figure 15. Half bandwidth 3σ for different selected data.
cases. The variation threshold of 0.2˚C/h was selected by trial and error. If it is too small, the number of samples in the selected band decreases considerably, which in return increases the value of the standard deviation.
Summarizing, it is stated that the bandwidth of a scatter diagram can be reduced by selecting a moderate band for temperature and its gradient and by limiting the absolute temperature change rates.
6. Conclusions
This paper presents monitoring data of a new bridge in Luxembourg, which is extremely sensitive to temperature effects due to constrained polymeric bearing pads and a very thick asphalt layer, whose Young modulus is known to be very temperature sensitive. The most relevant parameter for the eigenfrequencies and hence the bridge’s stiffness of this undamaged composite bridge is the concrete temperature, which varies more slowly than the steel temperature due to the higher thermal inertia.
A bridge does rarely have one constant temperature under real outside conditions, but this scalar value is a function of space and time, i.e.
Normal aging without relevant damage also leads to a reduction of stiffness in an important order of magnitude, which is more difficult to assess and compensate. On our bridge approximately 1% per year was found, an individual value for any bridge. Hence only repetitive testing or continuous monitoring may solve this issue.
Last but not least, it was also mentioned that the level of the excitation force influences the detected eigenfrequencies by some percent for this bridge, as can be seen in Figure 6. This parameter can be controlled by using appropriate exciters that control the acceleration or force range [18] or by extensive averaging of continuously monitored data.
Cite this paper
Nguyen, V.H., Mahowald, J., Schommer, S., Maas, S. and Zuerbes, A. (2017) A Study of Temperature and Aging Effects on Eigenfrequencies of Concrete Bridges for Health Monitoring. Engineering, 9, 396-411. https://doi.org/10.4236/eng.2017.95023
References
- 1. Kullaa, J. (2003) Damage Detection of the Z24 Bridge Using Control Charts. Mechanical Systems and Signal Processing, 17, 163-170.
https://doi.org/10.1006/mssp.2002.1555 - 2. Yan, A.M., Kerschen, G., De Boe, P. and Golinval, J.-C. (2005) Structural Damage Diagnosis under Varying Environmental Conditions—Part I, II. Mechanical Systems and Signal Processing, 19, 847-880.
https://doi.org/10.1016/j.ymssp.2004.12.002 - 3. Magalhaes, F., Cunha, A. and Caetano, E. (2012) Vibration Based Structural Health Monitoring of an Arch Bridge: From Automated OMA to Damage Detection. Mechanical Systems and Signal Processing, 28, 212-228.
https://doi.org/10.1016/j.ymssp.2011.06.011 - 4. Magalhães, F., Cunha, á. and Caetano, E. (2014) Five Years of Continuous Dynamic Monitoring of Infante D. Henrique Bridge. Proceedings of the 9th International Conference on Structural Dynamics, Eurodyn 2014, Porto, 30 June-2 July 2014, 2263-2270.
- 5. Peeters, B. and De Roeck, G. (2000) One Year Monitoring of the Z24-Bridge: Environmental Influences Versus Damage Events. Proceedings of the 18th International Modal Analysis Conference, San Antonio, 7-10 February 2000, 1570-1576.
- 6. Lloyd, G.M., Wang, M.L. and Wang, X. (2004) Thermomechanical Analysis of Long-Term Global Modal and Local Deformation Measurement of the Kishwaukee Bridge Using the Bootstrap. Earthquake Engineering and Engineering Vibration, 3, 107-115.
https://doi.org/10.1007/BF02668856 - 7. Gomez, H.C., Fanning, P., Feng, M.Q. and Lee, S. (2011) Testing and Long-Term Monitoring of a Curved Concrete Box Girder Bridge. Engineering Structures, 33, 2861-2869.
https://doi.org/10.1016/j.engstruct.2011.05.026 - 8. Soyoz, S. (2008) Long-Term Monitoring and Identification of Bridge Structural Parameters. Computer-Aided Civil and Infrastructure Engineering, 24, 82-92.
https://doi.org/10.1111/j.1467-8667.2008.00572.x - 9. Zabel, V., Brehm, M. and Nikulla, S. (2010) The Influence of Temperature Varying Material Parameters on the Dynamic Behavior of Short Span Railway Bridges. Proceedings of the 24th International Conference on Noise and Vibration Engineering, Leuven, 20-22 September 2010, 1519-1530.
- 10. Moaveni, B. and Behmanesh, I. (2012) Effects of Changing Ambient Temperature on Finite Element Model Updating of the Dowling Hall Footbridge. Journal of Engineering Structures, 43, 58-68.
https://doi.org/10.1016/j.engstruct.2012.05.009 - 11. Pirner, M., Fischer, O. and Urushadze, S. (2009) Long-Term Observation of Old RC Structures Using Dynamic Response. Proceedings of the IMAC-XXVII, 9-12 February 2009, Orlando.
https://sem.org/wp-content/uploads/2015/12/sem.org-IMAC-XXVII-Conf-s38p003-Long-term-Observation-Old-RC-Structures-Using-Dynamic-Response.pdf - 12. Au Francis, T.K. and Si, X.T. (2012) Time-Dependent Effects on Dynamic Properties of Cable-Stayed Bridges. Structural Engineering and Mechanics, 41, 139-155.
https://doi.org/10.12989/sem.2012.41.1.139 - 13. Bungard, V. (2011) Condition Assessment of Concrete Structures and Bridges Using Vibration Monitoring in Comparison to Changes in Their Static Properties. PhD Dissertation, University of Luxembourg, Shaker Verlag GmbH, Luxembourg City.
https://www.amazon.de/assessment-structures-monitoring-comparison-properties/dp/3844000771 - 14. van Overschee, P. and de Moor, B. (1996) Subspace Identification for Linear Systems: Theory, Implementation, Applications. Kluwer Academic Publishers, New York City.
https://doi.org/10.1007/978-1-4613-0465-4 - 15. Mahowald, J. (2013) Evaluation of Dynamic Damage Indicators on Real-Life Civil Engineering Structures: Measurement Uncertainty and Environmental Influences Considered. PhD Dissertation, University of Luxembourg, Shaker Verlag GmbH, Luxembourg City.
- 16. Moser, P. and Moaveni, B. (2011) Environmental Effects on the Identified Natural Frequencies of the Dowling Hall Footbridge. Mechanical Systems and Signal Processing, 25, 2336-2357.
https://doi.org/10.1016/j.ymssp.2011.03.005 - 17. Mahowald, J., Maas, S., Nguyen, V.H., Waldmann, D. and Zuerbes, A. (2014) Some Conclusions from the Measurements of Temperatures and Their Gradients on Eigenfrequencies of Bridges. Proceedings of the 9th International Conference on Structural Dynamics, Eurodyn, Porto, 30 June-2 July 2014, 2319-2323.
- 18. Maas, S., Zürbes, A., Waldmann, D., Waltering, M., Bungard, V. and De Roeck, G. (2012) Damage Assessment of Concrete Structures through Dynamic Testing Methods, Part 2, Bridge Tests. Engineering Structures, 34, 483-494.
https://doi.org/10.1016/j.engstruct.2011.09.018













