Received 18 March 2016; accepted 19 June 2016; published 22 June 2016

ABSTRACT

The electrification of powertrains leads to an increasing diversification of powertrain configurations. Each single configuration has its specific advantages which appear depending on the usage profile. To find the usage based optimal powertrain in consideration of a variety of evaluation criteria, the powertrains have to be optimized for the usage profile and characteristics have to be extracted from the usage profile. The carbon dioxide emissions of the optimized powertrains and usage based criteria are used in a multi-criteria decision analysis to determine the optimal powertrain for a specific usage profile. The description of characteristic maps forms the objective function of a minimization problem. The determined carbon dioxide emissions are one criterion in a multi-criteria decision process. All considered criteria are at least partly objective so that subjective ratings are eliminated as far as possible. The result is an optimized powertrain for a desired usage under the consideration of objective criteria that are extracted from the usage profile.

Keywords:

Multi-Criteria Decision Analysis, Analytic Hierarchy Process, Powertrain, Hybrid Electric Vehicle, Battery Electric Vehicle, Optimization

1. Introduction

The fulfillment of current and future legal requirements regarding the emissions of passenger cars has led to a progressive electrification of the powertrain. Subsequently the number of powertrain configurations has increased in recent years. This makes the identification of the most appropriate powertrain for a specific usage profile more difficult. To support the decision making process, a multi-criteria decision analysis based on objective criteria is proposed that uses the Analytic Hierarchy Process (AHP) [1] . There are several approaches in the literature for powertrain optimization. Amirian et al. [2] used the AHP for the decision between two motors variants for a series hybrid vehicle. The considered variants are discrete and not scalable. The comparison is performed for the Urban Dynamometer Driving Schedule (UDDS) which is part of the approval procedure in the United States. Scripcariu [3] proposes a method for the comparison of batteries for hybrid electric vehicle using the AHP. For the rating the criteria fuel consumption, DC-DC temperature and environmental impacts are chosen. The parameters for the different batteries concerning the decision criteria are taken from literature. Mehrkish et al. [4] also uses the AHP for the rating of different powertrain configurations for an existing vehicle under consideration of fuel consumption, costs and performance. Besides this approaches which are using the AHP for the comparison of variants, other approaches focus to a wide extend only on the fuel and energy consumption partly combined with a performance analysis [5] - [8] . The considered load cycles in each study are standardized cycles like the NEDC (New European Driving Cycle), UDDS or Artemis. All these cycles have in common that the individual usage is not considered. The configuration variants investigated in these approaches are limited and do not cover the variety of hybrid vehicle powertrain configurations. Eghtessad [9] focuses on user based load cycles for the dimensioning of a battery electric vehicle. The usage profiles are generated from a large database under consideration of key parameter. The torque and speed range of the electric machine are scaled according to the requirements of the generated cycle and additionally the gearbox is adapted to the cycle. This approach represents an optimized powertrain for a class of users. The proposed method in this paper focuses on the individual user and utilizes real driving cycles for the optimization of powertrain components and the weighting of the AHP criteria. The considered criteria are extracted from the usage profile and are the result of an optimization of the powertrain for the specific usage. The optimization process of the powertrains is described in detail in [10] . The present paper focuses on the structure of the decision making process and the extraction of characteristics from the usage profile. First, an overview of the optimization framework is given and the role of the decision making process within the framework is presented. Subsequently, the basics of the AHP are introduced. The extraction of usage based criteria from the usage profile forms the next section. With the presentation of the AHP structure for the present case the decision making process is determined. In the following section the results of the AHP are presented and the optimal powertrain for a specific usage profile is provided.

2. Optimization Framework

For an optimization in general it is necessary to define an objective criterion or function. They are determined by the requirements of the object of investigation. Besides the objective function additional objective criteria can be used which extend the problem to a multi-objective optimization problem. The term multi-objective refers in the present analysis to the set of criteria a powertrain has to meet. The solution alternatives are discrete and covernine different powertrain topologies. For the solution of the optimization problem a novel method is proposed. This method is a combination of an optimization algorithm and a multi-criteria decision making method. Figure 1 shows the process of usage based powertrain optimization which is explained below.

The investigated powertrains include conventional, hybrid and battery electric powertrains. They are used in combination with an analysis of the usage profile to determine an objective system and criteria as basis for the usage based optimization and the decision making process. Nonlinear programming is used under consideration of the usage profile and the powertrains. Abstracted characteristic maps for the fuel consumption of internal combustion engines (ICEs) and for the efficiency of electric machines are used within the optimization. The abstraction of the characteristic maps is performed with elliptic paraboloid. The detailed description of the abstraction process is presented in [10] .

The objective function for the optimization is the well-to-wheel carbon dioxide emission of the considered powertrain. For the determination of the carbon dioxide emissions a longitudinal backward simulation is used. Within this simulation the characteristic maps of the traction machines are represented by elliptic paraboloid. The shaping parameters of the elliptic paraboloids are the free parameter of the optimization. Reasonable restrictions ensure that the shaping of the paraboloids still represent a characteristic map. The variation of the free parameter by the optimization algorithm leads to a change of shape and position of the paraboloid. Additionally, the power output of the traction machines is adapted. The backward simulation determines the carbon dioxide emissions with the varied characteristic maps on the underlying usage profile. The optimization loop is passed until a defined stop criterion is satisfied. The resulting carbon dioxide emissions for the considered powertrain are minimal.

The obtained characteristic maps are used to determine the driving performance of the specific powertrain. Typical criteria for the evaluation of driving performance are considered and these criteria enter into the decision making analysis. The driving performance is determined with a forward simulation due to the fact that the speed trajectory isn’t known a priori. Subsequently the obtained data and the carbon dioxide emissions are used as characteristics within the decision making process. The process is based on the Analytic Hierarchy Process (AHP) [1] and determines the optimal usage based propulsion system by applying an eigenvalue method.

3. Analytic Hierarchy Process

The assessment procedure for the multi-criteria decision analysis used for the search for the optimal powertrain for a usage profile is based on the Analytic Hierarchy Process by Saaty [1] . The AHP structures the issue under consideration and permits the rating on the basis of measureable factors through a mathematical procedure [11] . With a consistent use of objective criteria subjective ratings become dispensable with the effect that an objective decision making process can be obtained. This qualifies the AHP in relation to other decision making techniques which rely on subjective assessments by the decision-maker [12] . The aim by using AHP is an objective ranking of the different powertrains. Therefore, characteristic values are extracted from the usage profile and the results of the optimization process respectively the results from the determination of the driving performance are used. The assessment structure forms an objective decision making process on the basis of usage based data.

In the following the characteristic values of the evaluation criteria from the usage profiles are deducted and transferred into a consistent rating scheme. The scheme is based on the fundamental scale by Saaty [13] . The scale reaches from 1 to 9 and is normally used to compare alternatives with regard to their importance. In this paper it is used to normalize the different characteristic values with different units to one scale. The value 1 means lowest rating for a property and 9 the highest rating.

3.1. Evaluation Criteria for Usage Profiles

To deduct characteristic values from a usage profile respectively the speed over time trajectory the signal has to be analyzed under different aspects. The total travelled distance is one considered parameter. This value has significance for hybrid and battery electric vehicle. With a one way driving distance below 10 km a lower electric range is not that relevant to the user as it will with a one-way distance over 50 km. The next parameter is the maximum speed. When high speeds are reached within the profile a higher rating for criterion maximum speed can be derived. For the classification of the dynamic user behavior the maximum acceleration between 0 - 50 km/h and 50-v_max is considered. In the lower speed range the maximum acceleration for a normal driver is assumed with 3 m/s² and in the higher speed range with 1.25 m/s². If higher accelerations in the usage profile occur a higher prioritization along with a higher rating is derived. The values for maximum torque and maximum power of the traction machine are not relevant for the rating scheme as these values are implicitly included in the considered parameter. Table 1 shows the scale for the rating scheme and the according values of the characteristics.

In conjunction with the driving performance determination through the forward simulation every powertrain alternative can be rated with the proposed scheme. Besides the driving performance that reflects individual preferences the carbon dioxide emissions of a powertrain have to obtain a higher weight within the AHP to underline their importance in a global manner. The ratio is set to 60%/40% for the carbon dioxide emissions. It should be noted that the ratio and the rating is inverted in the context of the Analytic Hierarchy Process due to the fact that a common basis for the driving performance and the carbon dioxide is needed.

3.2. Structure of the Rating Scheme

The implementation of AHP leads to a hierarchical structure of the rating scheme as shown in Figure 2. The focus of the decision making process is to find the usage based optimal powertrain. Therefore, the problem is subdivided into criteria and sub-criteria. The considered criteria are the CO₂ emissions and the driving performance. Driving performance and CO₂ emissions have an opposed tendency concerning the meaning what is a good rating. While lower values for the CO₂ emissions are rated advantageous some of the driving performance values are rated advantageous at higher values. To unify the orientation, the relevant driving performance criteria will be inverted when inserted into the pairwise comparison matrix. The weighting for the criteria concerning the focus is set to w_F1 = 0.4 for the CO₂ emissions and w_F2 = 0.6 for the driving performance according to the explanations stated above. These weighting factors are the only non-objective ones in the whole process.

The sub-criteria for the CO₂ emissions are the usage based driving cycles. A driving cycle characterizes a route travelled by the user. If there are more than one cycle (beside the usage profile used in the NLP and in the evaluation criteria, that is cycle 1) that should be considered for the ranking the weighting of the cycles is determined by concerning the travelled distance and frequency.

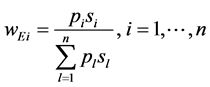(1)

The weighting w_Ei, 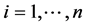of the cycles is calculated with the product of the cycle usage numbers p_i

and the travelled distance s_i in proportion to the total distance travelled. The index “E” stands for emission. For the rating the optimized powertrains are used and the resulting carbon dioxide emissions e_ik for the i-th cycle and the k-th powertrain are directly considered for the weighting. The pairwise comparison of the powertrains concerning the CO₂ emissions leads to a filling of the pairwise comparison matrix 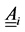with the proportions of the CO₂ emissions which read as follows

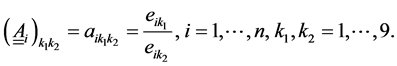(2)

The determination of the weighting vector requires a scaling of any column k₂ with the sum of its elements. The elements of the weighting vector can be obtained according to

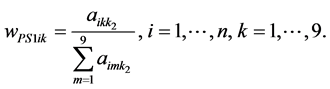(3)

The index “PS” stands for propulsion system. The rating of the powertrains with respect to the focus (cf. Figure 2) is calculated under the consideration of the CO₂ emissions as stated in 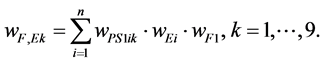(4).

(4)

The index “F” stands for focus. For the driving performance the sub-criteria are the maximum velocity of the

vehicle v_max, the acceleration in low speed range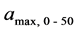, the acceleration in high speed range

and the range of the propulsion systems concerned. The weighting of the sub-criteria is done according to Table 1. With the data for the sub-criteria extracted from the driving cycle the transfer into a uniform rating scheme can be performed. This approach integrates the usage behavior into the decision making process and controls the weighting of the sub-criteria.

For the measurement of the driving performance of the optimized powertrains a forward simulation is used. A forward simulation is needed due to the fact that an adequate modeling of the tire road contact has to be implemented and the velocity over time behavior is not known a priori. The results from the driving performance simulation are used to fill up the pairwise comparison matrix and to calculate the weighting factors. The rating of the powertrains concerning the driving performance with regard to the focus is performed with

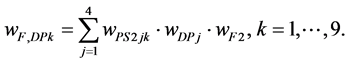(5)

The index “DP” stands for driving performance. The weights w_PS2jk describe the rating of the powertrains concerning the driving performance criteria. These criteria which are determined using the forward simulation are the maximum velocity v_max which is reachable with the considered powertrain, the full throttle acceleration time in the speed range 0 - 50 km/h t_0-50, the acceleration time from 0 - 100 km/h t_0-100 and the range on the considered cycle. It has to be taken into account that not the maximum accelerations but the acceleration times are the parameter for these two sub-criteria. The acceleration times are chosen due to the fact that the acceleration capability in a specific speed range is described in a better way by an integral value than by a single value. That means for the weighting of the acceleration sub-criteria in relation to the driving performance criterion the user preference is extracted from the driving cycle. The weighting of the alternatives in relation to the acceleration sub-criteria is performed by analyzing the simulation data concerning the acceleration times. The data extracted from the driving cycle describes the usage behavior. For the rating of the powertrains a propulsion system specific parameter has to be considered.

The summation of the weights w_F,Ek and w_F,DPk (see (6)) result in the total weight for one powertrain concerning the focus to find a usage based optimal powertrain

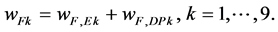(6)

With the calculation of the weights w_Fk for all considered powertrains the usage based optimal powertrain is identified by the choice of

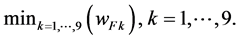(7)

The rating scheme provides the basis for decision making with objective data which is extracted from the usage profile and the dimensioning method. Through the consistent calculable weights subjective criteria are reduced to a minimum.

4. Results and Discussion

The results for two selected usage profiles will be discussed. Both profiles were measured in the metropolitan area of Hamburg, Germany. The first one is a cycle with merely urban driving and the second is a combined urban and motorway cycle. The characteristic values of the profiles are summarized in Table 2. For the consideration of the carbon dioxide emissions a well-to-wheel accounting method is used. In a global consideration the well-to-wheel analysis is the only reasonable approach, as disposal costs measured by CO₂ emissions are taken into account.

The first usage profile considered is the urban driving profile in the city of Hamburg (Figure 3). The vehicle data used for the simulation is validated through coast down tests and represent a compact class car.

From the perspective of the powertrain the urban cycle has low requirements for the power capability of the traction machines. Due to the different vehicle weights the power demand varies between the powertrain alternatives. The highest power is needed by the battery electric vehicle (BEV) and the serial hybrid vehicle (SHEV) because of the highest installed battery capacity along with the highest weight of all alternatives. This leads to the highest power demands. The lowest power is demanded by the petrol engine. With a vehicle weight of m_Petrol = 1465 kg the calculated weight is 195 kg under the vehicle weight of the SHEV with a diesel engine as range extender m_SHEV-D = 1660 kg. According to the weights the power demand differs approx. 27% (P_max,Petrol = 35.5 kW, P_max,SHEV-D = 45.2 kW). This illustrates that energy demand in form of electric or chemical energy for the same usage profile has a wide spread depending on the powertrain configuration. The results of the optimization for the urban profile are shown in Table 3. The emission factor for electrical power is set to 562 g CO₂/kWh [14]

which corresponds to the emission factor for Germany 2014. For the petrol engine, an emission factor of 309 g CO₂/kWh is assumed, and for the diesel engine a factor of 303 g CO₂/kWh [15] .

The highest carbon dioxide emissions are emitted by the petrol engine. With a high proportion of lower part load, the efficiency declines due to losses at the throttle. For the hybrid vehicle a differentiated consideration has to be made. While the power-split hybrid (PSHEV) show higher CO₂ emissions as the best internal combustion engine, the parallel (PHEV) and serial hybrid nearly halved the CO₂ emissions of the conventional powertrains. The lowest emissions for the urban profile are emitted by the battery electric vehicle with M_BEV´= 47 g CO₂/km. The power output of the electrical machine is reduced for this cycle to approx. 45 kW. The driving performance with this optimized powertrain are simulated and used for the rating scheme as presented above. The approach for the weight calculation will be shown by the example of the urban profile.

The determined CO₂ emissions for all considered powertrains are used in the pairwise comparison matrix A₁.

(8)

Due to the complete consistency of the pairwise comparison matrix with Rang(A₁) = 1 the eigenvector can be obtained through a normalization of any column with the sum of the column entries. The related eigenvalue λ_max = 9 can be calculated with the trace of A₁. The obtained vector equals the weighting vector w_PS11. For the first column it reads as follows

(9)

The entries of the vector are the weights of the powertrains concerning the CO₂ emissions for the urban profile. It has to be taken into account that lower values are advantageous as the optimal powertrain is the one with the lowest total weight. This is relevant because for some of the criteria like the maximum speed higher values are referred to as advantageous. These criteria are inverted when used for the pairwise comparison matrix. The maximum speeds determined for the optimized powertrains with the forward simulation are shown in Table 4.

With entry of the top speeds in a pairwise comparison matrix, the weighting vector can be obtained by using the same procedure as stated above.

(10)

The weightings are inverted for the reasons stated. This means that high maximum speed leads to a low weight. The weighting vectors for the other criteria read as follows

(11)

for the rating of the powertrains concerning the criterion acceleration time from 0 - 50 km/h and

(12)

for the acceleration time from 0 - 100 km/h. The ratios for the determination of the weights concerning the range are inverted and result in

(13)

Now all weightings of the powertrains concerning the sub-criteria are known and the weights of the sub-cri- teria concerning the criteria will be determined. For the considered case with only one cycle the weight w_E1 = 1. The weighting of the sub-criteria concerning the criteria requires the determination of the cycle characteristics. The maximum speed during the usage profile is v_max,1 = 61.1 km/h which leads to a rating of according to the rating scheme of Table 1. For the maximum acceleration in the lower speed range a_max,0-50 = 3.96 m/s² a rating of b_max,0-50 = 6.18 is obtained. The acceleration in the higher speed range lead to a rating of. The range is rated to b_R = 1.61 because of the total travelled distance of s_tot = 13.1 km. Die ratings are entered in the pairwise comparison matrix A_DP which contains the pairwise comparison of sub-criteria concerning the criteria driving performance.

(14)

With the matrix A_DP, the weighting vector for this part of the decision making process can be obtained

(15)

The high weight for the maximum speed w_DP1 = 0.391 shows the lower rating of the criterion due to the fact that the rating scheme is partly inverted and lower values are classified as advantageous. The same holds for the range with w_DP4 = 0.383. The high weighted maximum speed reflects the low speed level for the urban profile and the high weighted range reflects the short covered distance. For the criteria concerning the acceleration the ambitious acceleration behavior of the driver results in a lower weight for both criteria which is synonymous with a high relevance for the user.

In conjunction with the weighting between the criteria driving performance and emissions the total weights for the powertrain alternatives are obtained by aggregation in accordance with (4) and (5) and summation pursuant to (6). The results are shown in Figure 4. The optimization of the CO₂ emissions identified powertrains as advantageous for the urban profile that were able to complete the usage profile with electric energy only. The results of the AHP show a different orientation due to the additional extracted characteristics from the usage profile.

The horizontal line in Figure 4 represents the average weight. Powertrains which are rated below this line can be considered more suitable for the usage behavior than the powertrains with a weight over the horizontal line. Remarkable is the change in the rating for the BEV. While this propulsion system has the lowest carbon dioxide emissions for the urban profile the total weight in the rating scheme is the highest. This means that all other powertrain alternatives have to be preferred for this usage profile. The high weight results especially from a smaller range compared to the other propulsion systems and a performance below the average in the criteria concerning the acceleration. Contrary the Diesel constitutes an advantageous powertrain for the urban profile in a multi

criteria approach. Similarly, the parallel and serial hybrids show low total weights with the lowest weight for the parallel hybrid combined with a petrol engine.

The combined usage profile with a motorway proportion and an urban proportion has a significantly higher speed level and higher maximum speed than the urban profile. Figure 5 shows the speed and height over time plot for the combined urban motorway profile.

The combined usage profile can be subdivided into three parts. First urban driving for 3.1 km is passed. Subsequently a motorway part with a travelled distance of approx. 15 km is completed before again urban driving for approx. 2 km is conducted which leads to a total travelled distance of 20.1 km. The results of the powertrain optimization concerning the CO₂ emissions are shown in Table 5. The motorway proportion has a share of approx. 74% for this profile with the effect of another emphasis of the optimization result compared to the urban cycle. The Diesel is on the same level like the propulsion systems which are able to complete the cycle by electric driving. Furthermore, the difference between the highest and lowest emissions is lower. While in the urban cycle a factor of approx. 3.6 can be observed the factor reduces to 1.6 for the combined cycle. The efficiency advantage of the electric driven vehicles maintains but with increasing energy demand the difference lowers due to the high well-to-wheel emissions for the electrical power generation. This discrepancy leads to a lower weight of the efficiency advantage of electric machines which are charged from the grid when the energy demand for the profile increases. Propulsion systems that partly or solely using a combustion engine for the profile are relatively better weighted. Figure 6 illustrates this relationship. While all powertrains besides the diesel enginewhich are using a combustion engine in the urban cycle obtain weights above the average weight, the same types of powertrains are weighted on the same level or under the average weight for the combined profile. To the same extent the hybrid powertrains, especially the serial hybridslose compared to the above mentioned powertrains due to their higher total weight.

The proposed method for usage based optimization of the powertrain has shown its suitability by the results achieved for exemplary considered usage profiles. The multi criteria rating on the basis of objective data and simulation results enables the user to identify an advantageous powertrain configuration for the specific usage behavior.

5. Conclusions

The proposed method optimizes powertrains for a specific usage profile. In consequence, the determination of an optimal powertrain for a usage profile with regard to carbon dioxide emissions and individual usage behavior is provided. A decrease in CO₂ emission is achieved through the dimensioning of powertrain components. The emissions (as a result of a longitudinal dynamic simulation) form the objective function of the optimization problem. Taking the well-to-wheel emissions into account, not only the local emissions of the vehicle but the

global emissions are investigated in this study. The fitted powertrains are used to determine the driving performance and to evaluate the driving performance with respect to the usage behavior. In combination with the CO₂ emissions, an Analytic Hierarchy Process provides the usage based optimal powertrain under consideration of the specific usage on the basis of objective criteria.

The results show that the optimal powertrain for a specific usage has to fulfill a variety of requirements and that low CO₂ emissions alone are not sufficient. Rather it is necessary to meet the majority of requirements in a manner that suits the usage behavior. This leads for the considered urban cycle to advantageous ratings for PHEV and SHEV although their CO₂ emissions are higher than the emissions by the BEV. The BEV suffers from a short range and only average acceleration capability due to the higher weight. For the combined profile with urban and motorway proportion, the same statement for the BEV can be made. The diesel provides low CO₂ emissions and takes advantages from higher loads in the motorway proportion with the consequence of higher efficiency and lower CO₂ emissions. This leads to the lowest total weight in the AHP for this profile.

The consideration of auxiliary equipment under different ambient conditions is an influenced factor for further investigations. As the developed simulation model focuses on the conceptual comparison of powertrains, this point is not jet implemented. The consideration of heating and cooling capacity affects the conventional and alternative propulsion systems in a different manner with an advantage for the conventional propulsion systems concerning the process waste heat of the ICE. Another approach can be taken through the consideration of biogenic fuels which are nowadays to a small proportion part of the conventional fuels in Germany with the future perspective of a rising proportion.

Cite this paper

Tobias Hellberg,Martin Meywerk, (2016) Multi-Criteria Decision Analysis for Usage Based Optimization of Powertrains. Engineering,08,320-331. doi: 10.4236/eng.2016.86029

References