Engineering
Vol.08 No.02(2016), Article ID:63698,8 pages
10.4236/eng.2016.82007
Study on Rolling Characteristics of the Projectile with Wide-Angle Oblique Empennages
Bobo Zhao, Rongzhong Liu, Rui Guo, Lei Liu, Liang Chen
The College of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 January 2016; accepted 21 February 2016; published 24 February 2016
ABSTRACT
Due to requests on high rotary velocity of novel smart empennage-stable projectiles, the rolling characteristics under wide-angle oblique angles are studied. Since the wind tunnel tests performed verify numerical simulation, so that the latter method can be applied to study the rolling characteristics widely combining theoretical models. In the theoretical part, the rolling dynamics equations are established considering the span, taper ratio and oblique angle of the empennages, and are further solved combing ballistic equations. For the simulation, the rolling moment coefficients under various rotary velocities are solved based on rotating coordinate system methods, so that the balance rotary velocity can be obtained using interpolation. The results indicate that shorter span, higher taper ratio and especially larger oblique angle can bring higher projectile rotary velocity; the balance rotary velocity is approximately linear to the oblique angle in a certain range.
Keywords:
Wind Tunnel Test, Rolling Characteristic, Numerical Calculation, Ballistic Equation Style

1. Introduction
Large oblique angle can improve the lift force on empennage surface, and the differential configuration can provide sufficient rolling moment for the flying projectile, meeting the fighting technology requests on the novel low-altitude flying smart ammunition [1] . For example, considering small angle of firing and flat trajectory, the hedgehopping terminal sensitive projectile can meet rotary velocity requests due to sufficient rolling moment and displays scanning while flying. When some target is captured, the warhead can perform based on some rules for producing the high-efficiency damage on the armored target. Hence, study on the influence of wide-angle oblique empennages on projectile rolling characteristics is significantly meaningful to the development of novel ammunition.
Current relevant studies are mainly on the empennage design for realizing low rotary velocity and improving firing dispersion. Experiments are performed for studying the influence from oblique empennages and oblique- cutting empennages on the projectile velocity respectively, but the experimental method shows high cost on economy and time [2] [3] ; Numerical study on the rolling characteristics of the projectile with wide-angle oblique empennages is performed successfully, indicating that the numerical methods can simulate the rolling moment under small oblique angle well [4] [5] ; Reference [6] points out that under large attack angle, the wing will stall, and the lift drag characteristics will become nonlinear.
It can be found from previous literature that studies on the high-speed rotary projectile though designs of wide-angle oblique empennages are very few. Hence, study on influence of empennage structures on rotary velocity combing theoretical calculation and simulation is performed and the wind tunnel tests are performed for verification. Here, 4D ballistic equations are established for dynamics analysis on the wide-angle oblique empennages; the rolling moments under various empennages are calculation though numerical simulation whose validity has been confirmed using data from wind tunnel tests, so that the balance rotary velocity of the terminal sensitive projectile can be obtained.
2. Aerodynamic Numerical Simulation and Wind Tunnel Tests
As a high-speed rotary empennage-stable projectile, for keeping stable flight of the terminal sensitive projectile, the distance between centers of pressure and mass must have certain of stability margin. The oblique angle is defined as the included angle between the empennage root and projectile axis, δ, and the aerodynamic configuration applied is shown in Figure 1.
2.1. Aerodynamic Numerical Simulation
The rotating coordinate system can simulate the forced rotation with constant velocity efficiently though attaching circuity on the flow and the static coordinate system can be transformed to a rotating one though:
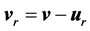 (1)
(1)
where, vr, v and ur are the relative velocity, absolute velocity and transport velocity respectively.
The Reynolds-average N-S equations under rotating coordinate system are used:
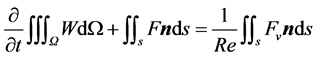 (2)
(2)
where, Q is the 3D control volume; W is the conserved quantity; F is the convective flux; Fv is the sticky flux, n is the outer normal vector of the control volume boundary surface. Finite volume method (FVM) is applied to discrete the space, and the implicit coupling algorithm based on the density, where the discretization scheme is selected as the Roe-FDS. Due to higher validity and accuracy, RNG k-ε model is applied for describing the turbulence flow. The flow-in boundary is set as the flow from the far pressure field, whose boundary is set as the free flow condition. The projectile boundary is set as the no sliding boundary condition.
Figure 1. Structural configuration of the hedgehopping terminal sensitive projectile.
The hexahedral structured grid is applied for meshing, and for obtaining accurate empennage aerodynamic characteristics, O-type topological structure is applied to densify grids close to the projectile body: 24D on the radial far field, 28D on the front axial far field and 36D on the back axial far field. The number of grid is 1.3 million, and the meshing can be seen in Figure 2.
2.2. Wind Tunnel Tests
The wind tunnel tests for the free rotary projectile have high requests on the model dynamic balance, strength, and test balance and so on. Hence, the static wind tunnel tests are performed to verifying the numerical simulation due to economy.
The tests are carried out by the HG-4 wind tunnel in Nanjing University of Science and Technology [7] , and the detailed experimental configuration is shown in Figure 3. Tests under Mach number 1.5 and 2 are performed (angle range is −2˚ to 8˚); a suitable scaling model is used; the choking phenomenon in the experimental zone is recorded by schlieren photography and high definition camera.
The template is used to format your paper and style the text. All margins, column widths, line spaces, and text fonts are prescribed; please do not alter them. You may note peculiarities. For example, the head margin in this template measures proportionately more than is customary. This measurement and others are deliberate, using specifications that anticipate your paper as one part of the entire journals, and not as an independent document. Please do not revise any of the current designations.
3. Theoretical Calculations on Dynamic Model
Setting the projectile center related to the empennage trailing edge as the coordinate origin, the projectile axis as the axis x, trailing edge direction as the axis y, a coordinate system on the oblique empennage can be established as shown in Figure 4.
From Figure 4 it can be seen that: due to large aspect ratio, the empennage can be simplified as an infinite flat plate, and test data of the lift coefficient slope can be used for the moment integration on the empennage surface; the angular moment, Mw is resulted from the lift difference by the oblique angle; the empennage additional attack angle is resulted from rotation; the empennage rolling moment, Mwf and rolling friction moment, MBf work as the rolling damping moment of this terminal sensitive projectile together.
Here, referencing the lift coefficient obtained, the moment can be calculated as:
Figure 2. Fluid field meshing.
Figure 3. Detailed experimental configuration.
Figure 4. Model and coordinate definition of the wide-angle oblique empennage.
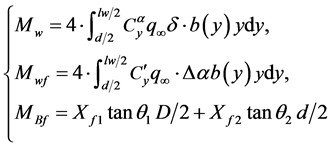 (3)
(3)
where, Cyα is the lift coefficient slope versus empennage oblique angle; 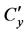 is the lift coefficient slope versus induced angle; Xf1, Xf2 are the friction forces of two projectile cylindrical parts respectively; θ1, θ2 are the included angles between friction force directions of two parts and projectile axis respectively. Under the combined effects of 3 moments, this terminal projectile will rotate and the rotary velocity can be described as:
is the lift coefficient slope versus induced angle; Xf1, Xf2 are the friction forces of two projectile cylindrical parts respectively; θ1, θ2 are the included angles between friction force directions of two parts and projectile axis respectively. Under the combined effects of 3 moments, this terminal projectile will rotate and the rotary velocity can be described as:
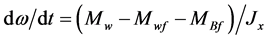 (4)
(4)
where, Jx is the projectile moment of inertia. In Equation (4), the projectile will achieve the static balance when the right term is equal to 0. Combining 3D equations of point-mass trajectory [8] :
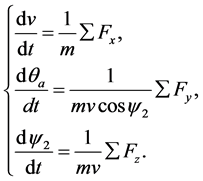 (5)
(5)
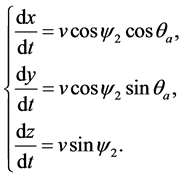 (6)
(6)
where, Fx, Fy and Fz are the force components of the terminal sensitive projectile in 3 coordinate axis respectively; x, y, and z are the projectile position under the ground coordinate system. Though solving the equations above, the projectile rotary velocity rules in the whole trajectory can be obtained.
4. Verification and Discussion
First, the wind tunnel test results are applied to verify the simulation method. Then, the projectile rolling characteristics are studied though combining theoretical analysis and numerical simulation.
4.1. Comparison of Wind Tunnel Tests and Numerical Simulation
In the test, the model with scaling proportion, 1:3.5, is used and the oblique angle is 13˚. The results from tests and simulation are compared in Figure 5.
Figure 5(a) indicates that the drag coefficient will increase along with the attack angle increase, and when the Mach number is relatively large, the results from tests are a bit higher than those from simulation; Figure 5(b) indicates that as the attack angle increases, the rolling moment coefficient will decrease and the results from tests are still a bit higher than those from simulation. In all, the results from simulation are close to those from tests, so the numerical simulation is very efficient, and can be applied for further analysis.
4.2. Analysis on Projectile Rotary Velocity
The basic structural parameter of this projectile is: projectile diameter (D), 125 mm; tail rod diameter, 0.4D; empennage span, 2.7D; empennage chord, 0.28D; projectile mass, 30 kg; polar moment of inertia, 0.1; initial velocity, 800 m/s; initial firing angle, 8˚.
Though applying the 4-order Runge-Kutta method to solve the 4D ballistic equations, the rotary velocity curves under different oblique angles can be obtained. Figure 6 indicates that: as the flying velocity increases, the projectile rotary velocity will increase dramatically first, and then decrease linearly and slowly after passing the peak position (660 m/s); when the flying velocity is close to 1 Ma, the rotary velocity will fluctuate lightly.
The results above can be explained as: in the initial part, the rolling moment provided by empennage lift is relative large, making the rotary velocity increase continuously, but as the rotary velocity increases, the overall rolling damping moment will increase, which will counteract the rolling moment generally and tend to a balance

Figure 5. Result comparison of wind tunnel tests and numerical simulation. (a) Drag coefficients versus attack angle; (b) Rolling moments versus attack angle.
Figure 6. Rotary velocity curves versus oblique angle.
so that the rotary acceleration will tend to 0; as the flying velocity continue to decrease, the rotary acceleration will become negative, making the rotary velocity decrease. It must be noted that when the flying velocity is close to the sound velocity, the flow field is very complicated and the empennage lift coefficient slope changes dramatically, making the rotary velocity fluctuate.
And, the relationships between rotary velocity and empennage span are shown in Figure 7 (oblique angle: 13˚).
It can be seen from Figure 7 that as the empennage span length decreases, the rotary velocity will decrease first and the peak will move right, but the rotary velocity will increase after passing the peak position. The results above can be explained as: 1) the calculation values from ballistic equations have larger phase difference than the balance rotary velocity, since the span decrease will make the rolling moment decrease, and a relatively little rolling moment will bring some lagged effects on the rotary velocity change; 2) the span decrease will change the moment distribution on the empennage, and the balance rotary velocity has a reverse relationship with the span length approximately, so that the balance rotary velocity can be improved significantly.
In addition, keeping the empennage area as a constant, the influences of the taper ratio on the balance velocity are shown in Figure 8 (Ma = 1.5).
From Figure 8, it can be found that as the taper ratio increases, the balance rotary velocity will increase by 13% approximately. This find can be explained as: when the empennage area is constant, as the taper ratio increases, the empennage area component which is close to the tip will decrease when the component close to the root will increase; under high rotary velocity conditions, the induced attack angle near the tip will be still over the oblique angle so that the force in the tip position will reverse when the force in the root position is still normal. Due to the factors above, the balance rotary velocity will increase.
The balance velocity where the rolling coefficient is equal to 0 is the static balance rotary velocity. Figure 9 indicates that as the empennage oblique angle increases, the rolling moment coefficient will decreases linearly.
Figure 10 indicates that the simulation results match those from theoretical calculation well, with error degree below 2%. Hence, the simulation method is very valid.
Figure 7. Rotary velocity curves versus empennage span.
Figure 8. Rotary velocity curves versus taper ratio, η.
Figure 9. Rolling moment coefficient versus rotary velocity.
Figure 10. Balance rotary velocity results by theoretical and numerical calculation respectively (Ma = 1.5).
Further, since the real rotary velocity is over the balance rotary velocity (Ma = 1.5) in the ballistic equations, the fitting results are modified as:

where, n is the rotary velocity modification coefficient in the ballistic equations, 1.04. It can be found that the rotary velocity is linear to the oblique angle (<16˚) based on the Equation (7).
5. Conclusions
Based on previous analysis on the rolling characteristics of the projectile with wide-angle oblique empennages, 3 main conclusions can be obtained:
1) Though comparison validation of the wind tunnel tests and numerical simulation, it is found that the numerical method is very valid for solving the projectile aerodynamics characteristics; as the attack angle increases, the projectile drag coefficient will increase and the rolling moment coefficient will decrease.
2) Rotary velocity is solved through theoretical calculation and numerical simulation respectively, and the former one can obtain the rotary velocity parameters versus time rapidly when the latter one can simulate the rolling mechanism well and the balance rotary velocity can be further obtained by interpolation. Results by two methods can match well.
3) The calculation results of rotary velocity are on basis of the verification from wind tunnel tests on the numerical simulation; hence, for better solution on the projectile rolling characteristics under wide-angle oblique empennages, more wind tunnel tests are necessary.
Cite this paper
Bobo Zhao,Rongzhong Liu,Rui Guo,Lei Liu,Liang Chen, (2016) Study on Rolling Characteristics of the Projectile with Wide-Angle Oblique Empennages. Engineering,08,60-67. doi: 10.4236/eng.2016.82007
References
- 1. Yang, S.Q. (2010) Smart Ammunition Engineering. National Defence Industry Press, Beijing.
- 2. Jenke, L.M. (1975) Experimental Roll-Damping Magnus, and Static Stability Characteristics of Two Slender Missile Configurations at High Angles of Attack (0 to 90 deg) and Mach Numbers 0.2 through 2.5. AEDC-TR 76-58.
- 3. Cheng, J., Wang, X.M., Yu, J.Y. and Yao, W.J. (2015) Study on the Effect of Sub-Caliber Asymmetry Canards on the Aerodynamics of Trajectory Correction Projectiles. Transactions of Beijing Institute of Technology, 35, 133-138.
- 4. Sahu, J. (2007) Numerical Computations of Dynamic Derivatives of a Finned Projectile Using a Time Accurate CFD Method. AIAA Atmospheric Flight Mechanics Conference and Exhibit, South Carolina, 20-23 August 2007, AIAA 2007-6581.
http://dx.doi.org/10.2514/6.2007-6581 - 5. Bhagwandin, V. (2012) Numerical Prediction of Roll Damping and Magnus Dynamic Derivatives for Finned Projectiles at Angle of Attack. 30th AIAA Applied Aerodynamics Conference, New Orleans, 25-28 June 2012, AIAA 2012-2905.
http://dx.doi.org/10.2514/6.2012-2905 - 6. Qian, W.Q. and Cai, J.S. (1999) Numerical Simulation of Turbulent Flow Past Airfoil at Low Mach Number. Acta Aeronautica et Astronautica Sinica, 20, 261-264.
- 7. Deng, F., Chen, S.S., Tan, X.Z. and Xu, T. (2010) Investigation of Aerodynamic Characteristics of Canard Configuration Long-Range Missile with Different Tails in Transonic and Supersonic Flow. Journal of Experiments in Fluid Mechanics, 24, 46-50.
- 8. Miller, F.P., Vandome, A.F. and Mcbrewster, J. (2010) External Ballistics. Alphascript Publishing, 105-185.










