Engineering
Vol.07 No.09(2015), Article ID:59776,9 pages
10.4236/eng.2015.79052
A Smoothing Neural Network Algorithm for Absolute Value Equations
Feiran Wang, Zhensheng Yu, Chang Gao
College of Science, University of Shanghai for Science and Technology, Shanghai
Email: zhenshengyu@usst.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 July 2015; accepted 17 September 2015; published 21 September 2015
ABSTRACT
In this paper, we give a smoothing neural network algorithm for absolute value equations (AVE). By using smoothing function, we reformulate the AVE as a differentiable unconstrained optimization and we establish a steep descent method to solve it. We prove the stability and the equilibrium state of the neural network to be a solution of the AVE. The numerical tests show the efficient of the proposed algorithm.
Keywords:
Absolute Value Equations, Neural Network, Smoothing Function, Linear Complementarity Problem

1. Introduction
Consider the following absolute value problem [1] -[3] :
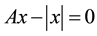 (1)
(1)
where ,
, 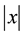 is absolute value of x, it is a subclass of absolute value equations
is absolute value of x, it is a subclass of absolute value equations 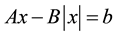 which is proposed by Rohn [4] , and it is a NP-hard problem [1] .
which is proposed by Rohn [4] , and it is a NP-hard problem [1] .
The AVE has closed relation with some important problems, for example, the linear programming, Quadratic programming problem and the bimatrix game problem. The above problems can be transformed into the linear complementarity problem, and the linear complementarity problem can be transformed into the absolute value equations. Due to its simple and special structure and application value, the research on absolute value equation has drawn attention of many researchers. Mangasarian [5] pointed out the relationship between backpack feasibility problem and the AVE. The problem of AVE has been studied deeply by Yamashita and Fukushima [6] , and the results of the research on the problem of AVE are applied to the problem of location selection, good results are obtained. The numerical solution methods of AVE, such as Newton method, quasi-Newton method, are reachable in [7] -[12] .
In this paper, we present a smooth approximation function which is based on neural network method to solve the AVE. By using a smooth approximation function of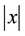 , we turn it into a differentiable unconstrained optimization problem. Furthermore, we obtain the approximate solution of the original problem based on our established unconstrained optimization problem and the neural network model. Compared with the Newton method, the neural network model needs less requirement for the hardware of compute and the iterative process is real-time.
, we turn it into a differentiable unconstrained optimization problem. Furthermore, we obtain the approximate solution of the original problem based on our established unconstrained optimization problem and the neural network model. Compared with the Newton method, the neural network model needs less requirement for the hardware of compute and the iterative process is real-time.
2. The Smoothing Reformulating of AVE
The absolute value Equation (1) is equivalent to the nonlinear equations:
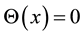 (2)
(2)
where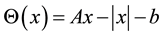 . Since it is a non smooth function, we construct a smooth function to approximate it.
. Since it is a non smooth function, we construct a smooth function to approximate it.
Definition 1.1 Smoothing approximation function, given a function , smoothing function
, smoothing function  is called smoothing approximation function, if for any
is called smoothing approximation function, if for any , there exists
, there exists 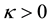 so that
so that
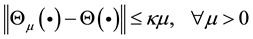
where 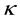 is not dependent on the x.
is not dependent on the x.
In this paper, we use the aggregate function [13] to give a smooth approximation of the absolute value equation:
Let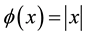 , so every component of the absolute value function can be recorded as
, so every component of the absolute value function can be recorded as
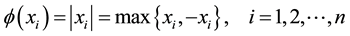
For any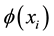 , the definition of smoothing function is as follows
, the definition of smoothing function is as follows
So the function of absolute value 
Thus the absolute value equation is transformed into the following smooth equations

where
We define the function as follows
where 


of the neural network. Thus, the approximate solution of the absolute value equation is transformed to the global optimal solution of the optimization problem
3. Neural Network Model for Absolute Value Equation
Consider the following unconstrained optimization problem

the gradient can be calculated by the following formula:
where
now, we can give a neural network model for solving the absolute value equation, which is based on the steepest descent neural network model for (4).

where 


4. Analysis of Stability and Existence
Next, we recall some materials about first order differential equations (ODE) [17] :

where 

Definition 3.1 A point 
if 




then 
Lemma 3.1 Assume that 






Definition 3.2 (Asymptotic stability). An isolated equilibrium point 
in addition to being Lyapunov stable, it has the property that 

Definition 3.3 (Lyapunov stability). Stability in the sense of Lyapunov Let 



such that 

Definition 3.4 (Lyapunov function). Let 




Figure 1. The block diagram of neural network (5).
Lemma 3.2 a) An isolated equilibrium point 

b) An isolated equilibrium point 
neighborhood 


Lemma 3.3 [11] For any



Theorem 3.1 

Proof. Let 
1) The function 




2) Since
3) If 

So, by the Definition 3.4 we know that 

Theorem 3.2 Each solution of the absolute value equation is the equilibrium point of the neural network (5).
Conversely, if
Proof. Assume that 




Obviously, we got

hand if 


Next, we can prove that 
Theorem 3.3. Let the 

Proof. Since 

uation is known by the Theorem 3.2. Therefore,
point, so 



Theorem 3.1 we know that 




Consequently, we have

5. Numerical Experiment
In this section we give some smooth of numerical tests of neural network algorithm, due to the complementarity problem can be transformed to absolute value equations, we consider the linear complementarity problem which is equivalent to the absolute value equations as test cases.
For a given matrix 




From the Theorem 2 in the literature [11] , if 1 is not the eigenvalues of the matrix

where 

Example 1 [11] . Consider the following linear complementary problem:
Since1 is not included in the eigenvalues of
where
We can find that 
By using the neural network model, the initial point is generated by x0 = rand (n,1), and the program is performed under the environment of MATLAB7.11.0. The following two figures (Figure 2 and Figure 3) describe how the approximate solution of example 1 and the energy function varies with time.
Figure 2. Transient behavior of x(t) of example 1.
Figure 3. Transient behavior of energy function of example 1.
Since


Example 2 [11] . Consider the following linear complementary problem:
Through calculation, we can get one eigenvalue of 





Set



And the absolute value equation is
Thus, we can get one solution of the absolute value equation whcih is
Since

Example 3. Consider the following linear complementary problem:
Figure 4. Transient behavior of x(t) of example 2.
Figure 5. Transient behavior of energy function of example 2.
Through calculation we can get one eigenvalue of 

And the absolute value equation is:
Thus, we can get the solution of the absolute value equation which is
Since
6. Conclusion
This paper adopted the aggregate function method to tackle the absolute value equation with smooth processing, and then turned the absolute value equation into a differentiable unconstrained optimization problem. In order to obtain the approximate solution of the original problem we use the proposed neural network model to solve the
Figure 6. Transient behavior of x(t) of example 3.
Figure 7. Transient behavior of energy function of example 3.
unconstrained optimization problem. At the same time, we propose one neural network which is based on different energy function. Through the transformation between linear complementary problem and absolute value equation, it can be used to solve the linear complementary problem, too. For the traditional energy function based on the NCP function, we can avoid a lot of matrix calculation. Numerical examples show that the algorithm is very effective for solving this kind of absolute value equation, and the accuracy of solution can be controlled by the parameters completely. In view of the fact that it is relatively difficult to solve the absolute value equation, the proposed method in this paper can be used to solve the absolute value problem effectively.
Acknowledgements
This work is supported by National Natural Science Foundation of China (No.11171221) and Innovation Program of Shanghai Municipal Education Commission (No.14YZ094).
Cite this paper
FeiranWang,ZhenshengYu,ChangGao, (2015) A Smoothing Neural Network Algorithm for Absolute Value Equations. Engineering,07,567-576. doi: 10.4236/eng.2015.79052
References
- 1. Mangasarian, O.L. and Meyer, R.R. (2006) Absolute Value Equations. Linear Algebra and Its Applications, 419, 359-367.
http://dx.doi.org/10.1016/j.laa.2006.05.004 - 2. Rohn, J. (2004) A Theorem of the Alternatives for the Equation Ax + B|x| = b. Linear and Multilinear Algebra, 52, 421-426.
http://dx.doi.org/10.1080/0308108042000220686 - 3. Han, J.Y., Xiu, N.H. and Qi, H.D. (2006) Nonlinear Complementary Theory and Algorithm. Shanghai Science and Technology Press, Shanghai.
- 4. Rohn, J.R. (1989) Systems of Linear Interval Equations. Linear Algebra and Its Applications, 126, 39-78.
http://dx.doi.org/10.1016/0024-3795(89)90004-9 - 5. Mangasarian, O.L. (2009) Knapsack Feasibility as an Absolute Value Equation Solvable by Successive Linear Programming. Optimization Letter, 3, 161-170.
http://dx.doi.org/10.1007/s11590-008-0102-9 - 6. Yamashita, S. and Fukushima, M. (2001) A Branch-and-Bound Method for Absolute Value Program and Its Application to Facility Location Problems. Kyoto University, Kyoto.
- 7. Mangasarian, O.L. (2013) Absolute Value Equation Solution via Dual Complementarity. Optimization Letters, 7, 625-630.
http://dx.doi.org/10.1007/s11590-012-0469-5 - 8. Mangasarian, O.L. (2009) A Generalized Newton Method for Absolute Value Equations. Optimization Letters, 3, 101-108.
http://dx.doi.org/10.1007/s11590-008-0094-5 - 9. Caccetta, L., Qu, B. and Zhou, G.L. (2011) A Globally and Quadratically Convergent Method for Absolute Value Equations. Computational Optimization and Applications, 48, 45-58.
http://dx.doi.org/10.1007/s10589-009-9242-9 - 10. Rohn, J. (2009) An Algorithm for Solving the Absolute Value Equation. Electronic Journal of Linear Algebra, 18, 589-599.
- 11. Yong, L.Q. and Tuo, S.H. (2012) Quasi-Newton Method to Absolute Value Equations Based on Aggregate Function. Journal of System science and Mathematics, 32, 1427-1436.
- 12. Yong, L.Q., Liu, S.Y. and Tuo, S.H. (2014) Transformation of the Linear Complementarity Problem and the Absolute Value Equation. Journal of Jilin University (Science Edition), 4, 638-686
- 13. Li, X.S. (1991) The Aggregation Function Method for Solving the Problem of Nonlinear Mini-Max Problem. Computational Structural Mechanics and Its Application, 8, 85-92.
- 14. Chen, J.-S., Ko, C.-H. and Pan, S.H. (2010) A Neural Network Based on the Generalized Fischer-Burmeister Function for Nonlinear Complementarity Problems. Information Sciences, 180, 697-711.
http://dx.doi.org/10.1016/j.ins.2009.11.014 - 15. Ma, H.Q. and Huang, N.-J. (20145) Neural Network Smoothing Approximation Method for Stochastic Variational Inequality Problems. Journal of Industrial and Management Optimization, 7, 645-660.
- 16. Liao, L.Z., Qi, H.D. and Qi, L.Q. (2001) Solving Nonlinear Complementarity Problems with Neural Networks: A Reformulation Method Approach. Journal of Computational and Applied Mathematics, 131, 343-359.
http://dx.doi.org/10.1016/S0377-0427(00)00262-4 - 17. Miller, R.K. and Michel, A.N. (1982) Ordinary Differential Equations. Academic Press, Waltham.




































