Engineering
Vol.6 No.2(2014), Article ID:42695,7 pages DOI:10.4236/eng.2014.62010
Efficient Performance Analysis of Spectrum Sensing for Cascaded Multihop Network over Nagakami-m Fading Channels
1Department of Electronics and Communication, Dr B R Ambedkar NIT, Jalandhar, India
2Jamia Hamdard University, Delhi, IndiaEmail: kakkard@nitj.ac.in
Copyright © 2014 Deepti Kakkar et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Deepti Kakkar et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 28, 2013; revised December 28, 2013; accepted January 5, 2014
Keywords: Spectrum Sensing; Energy Detection; Nakagami-m Wireless Link; Probability of Detection; Relay Protocol; Cascaded Multihop Communication
ABSTRACT
Performance evaluation of spectrum sensing in infrastructure based multihop network is very hard to achieve because of the adverse effects of channel fading. In this paper, performance of a multihop link is studied over Nakagami-m distribution. It provides the exact theoretical methodology for the performance analysis of spectrum sensing by evaluating detection probability. Using a cascaded multihop model, the end-to-end Signal to Noise Ratio (SNR) is given over Nakagami-m distribution. In the analysis, multihop model based on relays are considered over independent and not identically distributed (i.n.i.d) wireless channels. Simulation results show the effect of increase in number of hops on probability of detection for multihop links. Subsequent to the thorough fading severity analysis, it has been accomplished that spectrum hole detection is more crucial at lower SNR values with large number of hops.
1. Introduction
Cognitive Radio (CR) may be considered as a truly smart device talented of selecting its own band of action and deciding for certified or uncertified access. The keystone of the practically realizable CR network is the excellent organization of the spectrum sensing. The task of obtaining awareness about the spectrum usage and existence of PU’s in a geographical area is the main concern of spectrum sensing. The parameters viz. SNR in a wireless link, sensing time and threshold level plays an important role for the performance measurement of energy detection based spectrum sensing. Systems in unlicensed frequency bands can achieve great spectrum efficiency but have faced an inference that limits network capacity and scalability. Among all spectrum sensing techniques, energy detection is the most popular method because of its low computational complexities [1-3]. In the literature
[4,5], many research efforts have been expended to analyze the performance of energy detectors. However, an optimal spectrum sensing framework is introduced by [6] considering both spectral efficiency and interference between licensed and unlicensed user. The authors also illustrate the advantages of cooperative sensing. Co-operation improves detection performance for CRs. Multiple SU’s work collaboratively for the detection of white spaces. Some SU’s, who are far away from wireless link, might have a lesser amount of chance of detecting the PU transmission than the other. Sometimes a single secondary sensor might suffer from different kinds of interference. All the SU’s report to the fusion center about their sensing results. Each SU performs sensing and forwards the decision to the fusion center [7,8]. In fusion center, different diversity techniques can be functional, such as maximal ratio combining (MRC), equal gain combining (EGC) and square-law combining (SLC) [9]. The secondary access point makes a final decision for PU activity. The number of fusion rules can be incorporated at the fusion center, by considering two main assumptions that the channels are error free and SNR of primary signals are known to SUs [10-12]. In [13], authors focused upon different fusion strategies corresponding to data fusion and decision fusion in cooperative multihop environment over Rayleigh fading channel. Some preliminary work on spectrum routing has been proposed for joint channel assignment by [14]. Channel assignment strategy clearly reflects that the wireless channel is an important parameter in performance analysis of energy detector. So, signal propagation issues need to consider such as shadowing and severe multipath fading. Resource sharing with spectrum sensing plays an important role to enhance the system performance [15,16]. But primarily all discussed the concert for two hop relay networks. CR has not been discussed much for cascaded multihop scenarios with relay nodes in a wireless link. Multi-hop wireless ad-hoc systems are characterized by inefficient static spectrum allocations, imperfect channel distributions, fixed radio frequency bands, and imperfect network coordination. Due to higher potential of wider coverage in low transmitting power, multi-hop scenarios are gaining more concentration in wireless communication technologies [17]. Multihop scenarios are the best suitable example for practical radio transmissions. In the last years, numerous contributions addressed the performance of multihop relayed transmission. In [18], authors investigated the same performance problem of multihop relay link over different fading channels. A cascaded multihop framework is developed in [19]. Multihop transmission is accomplished through several relays between source and receiver. Relays can be classified as regenerative and non-regenerative. In [20], authors derived efficient performance bounds for multihop wireless communications systems with non-regenerative fixed-gain relays operating over non-identical generalized fading channels. Specifically, the end-to-end (SNR) is formulated and upper bounded. Based on this bound, the closed form solutions for the moments of the end-to-end SNR over generalized fading channels are obtained. In [21], authors derived closed-form expressions for the Average Bit Error Probability (ABER) for different modulation schemes of an amplify-and-forward average power scaling dual-hop relay transmission, over Nakagami-m faded wireless channels, with integer values of m. Further, performance evaluation using different diversity techniques for relay transmission schemes is evaluated by [22]. From the literature, it has been concluded that the Nakagami-m fading is generalized fading channel in multipath wireless communication with channel gain hi as a random variable between all nodes. Nakagami-m fading is defined by parametric gamma function for its rapid fading in high frequency long distance propagation. Power of the Nakagami distribution follows the gamma distribution with severity parameter m ranges from 1/2 to ∞. For special case of m = 1, the distribution reduces to Rayleigh distribution [23]. Following this line, in this contribution we are interested in the performance analysis of multihop wireless link over Nakagami-m fading distribution. We consider probability of detection (Pd) as performance metrics.
The remainder of paper is organized as follows: Section 2 briefly describe the system model of cascaded relays based wireless link. In Section 3, performance analysis of energy detection in Additive White Gaussian Noise (AWGN) channel is described and the closed form solution of probability of detection expressions in terms of circular contour integral for multihop cooperative scenario in Nakagami-m fading is derived. The corresponding expressions for equivalent SNR PDF, MGF, CDF and moments for the assumed model are introduced. Section 4 provides performance results and discussion. Finally, in Section 5, we sum up the conclusions of our studies.
2. System Model
Multihop transmission in wireless networks e.g. cellular and ad-hoc networks has been researched in the recent period due to its advantages over traditional networks for a variety of reasons. Relays are used to provide maximum coverage range with high transmission rate. In cellular communications, multihop networks are also very advantageous in terms of deployment and connectivity. Because of the increased spatial reusability of relays, the transmitter power required at the transmitter also reduces. In terms of CRs, the multihop networks can provide better spectrum utilization, if the numbers of relays within a wireless link are suitably chosen. Schematic of a multihop transmission link with primary source (PU-S), Primary receiver (PU-D) and (L-1) intermediate relay nodes is shown in Figure 1. In such systems, signal from source to destination propagates via several intermediate relay nodes with wireless channel in between two nodes. The shorter the distance between any two relays in multihop network results in reduction in path loss, hence reduction in total transmission power. In addition to this interand intra-cell interference level also reduces, leading to the higher capacity gain. Depending upon the nature and complexity, relay protocols can be regenerative and non-regenerative [24,25]. Assuming that all the cascaded relays between (PU-S) and (PU-D) share the same licensed frequency with bandwidth B. In the (PU-S) the input data is generated in the form of random numbers. The length of bits depends upon the type of modulation. With the help of randomization the long sequence of continuous ones and zeros are avoided.

Figure 1. System model of cascaded relays based multi-hop communication system.
By applying proper source coding and interleaving techniques, the data is arranged in a block format. Further desired modulation scheme is implemented for multihop transmissions.
When direct path wireless link between (PU-S) and (PU-D) is found to be bad, then the SU senses the wireless link with number of relay node between (PU-S) and (PU-D). In this system model reliable spectrum sensing performance is subjected to channel uncertainty constraint and relay characteristics. Each communication between cognitive relay occurs in orthogonal channels to avoid the inter-channel interference. Frequently used fading distribution to characterize the signal statics is Nakagami-m distribution. We assume that sub-channels between relay nodes and direct path are independent and are Nakagami-m flat fading channels. The noise is added at the relays and this noise is considered as the AWGN signal. In case of severe fading conditions, the transmission from source S to destination D fail if signal at any of the L hops fall below the required threshold SNR γth. If a symbol transmitted by the source S is successfully decoded by (L-1)th relay i.e. no intermediate relay in the link is down, the SNR at destination D statistically determined by SNR of the last hop. Hence, the statistics of SNR at destination D depends only on Lth hop provided that no other interfering source is present. The cascaded multihop DF relay link can be reduced to an equivalent point-to-point link. By following the approaches proposed in [19] the PDF of the end-to-end SNR can be expressed as
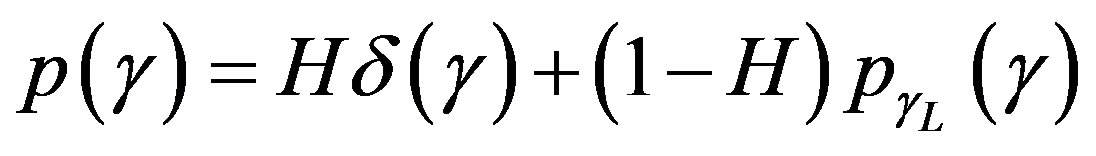 (1)
(1)
where, H represents joint probability that outage occur with first (L-1) hops and 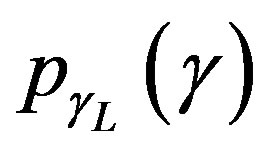 represent the SNR of Lth hop. Assuming channels of L hops as independent and not identically distributed (i.n.i.d) and relays in Figure 1 are separated by sufficient distance to avoid any interference, the probability H can be expressed as
represent the SNR of Lth hop. Assuming channels of L hops as independent and not identically distributed (i.n.i.d) and relays in Figure 1 are separated by sufficient distance to avoid any interference, the probability H can be expressed as
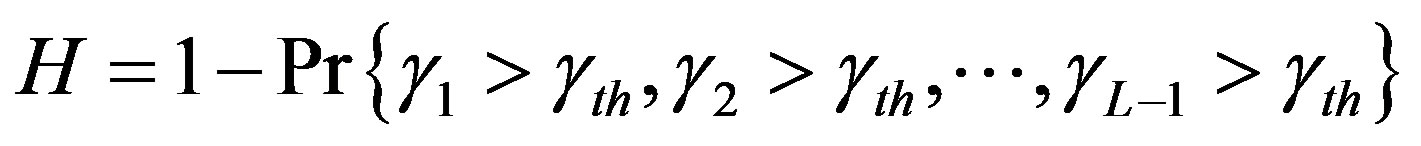 (2)
(2)
 (3)
(3)
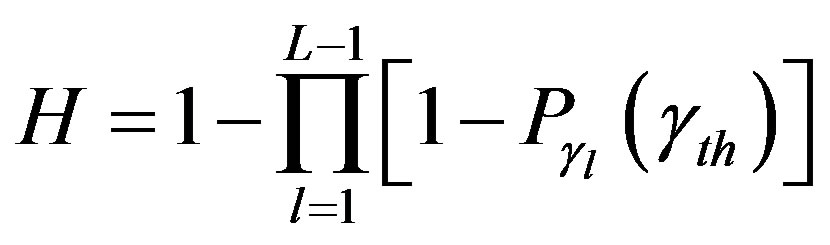 (4)
(4)
where,  is the Cumulative Distribution Function (CDF) of γl. The primary signal is assumed to be s(t) with multiple cascaded relays employ different relaying mechanisms to transmit the received signal.
is the Cumulative Distribution Function (CDF) of γl. The primary signal is assumed to be s(t) with multiple cascaded relays employ different relaying mechanisms to transmit the received signal.
3. Performance Analysis
3.1. Basic Energy Detector
In the energy detection in AWGN channel, the received signal x(t) takes the form x(t) = h*s(t) + n(t). Where h*s(t) is the channel impulse response and n(t) is the AWGN. The received signal is first pre-filtered by an ideal band-pass filter with transfer function to limit the average noise power and normalize the noise variance. The squared and integrated output is used to finally construct a measure of the energy of the received waveform. The detected energy is further compared with a predefined threshold which depends on the noise floor, and if detected energy is below than the predefined threshold then it is assumed that licensed spectrum is free otherwise if the detected energy is above than the predefined threshold value then it is assumed that licensed spectrum is occupied by the PUs hence determining the presence or absence of the licensed user’s spectrum. The performance of energy detection can be efficiently characterized in terms of detection probability and false alarm probability. In this model, Nakagami-m flat fading environment is considered. The distribution function of Nakagami-m fading is given by
 (5)
(5)
where Γ(.) is the Gamma function, Ω = y2 is the average power where y is Nakagami distribution envelope and m is fading parameter. Since Nakagami distribution encompasses scattered, reflected and direct components of the original transmitted signal, the output of the energy detector acts as the test statistic to test the two hypothesis H0 and H1 at particular instant of time (t) and can be represented as
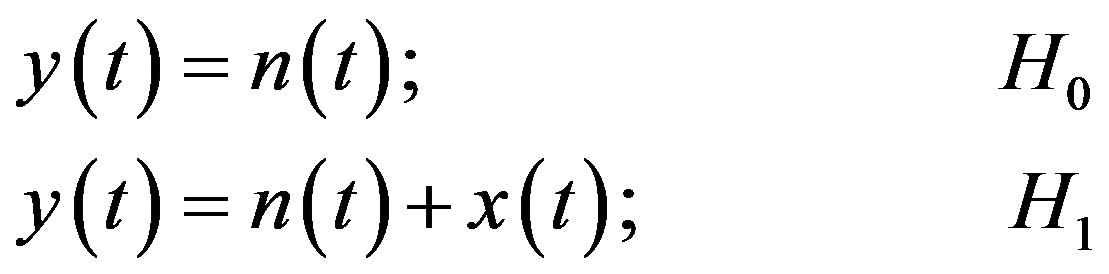 (6)
(6)
The hypothesis H0 describes that only noise is the present without signal within a channel and hypothesis H1 describes that the signal and noise both are present within the channel. The probability density function (PDF) of the received signal for hypothesis H0 and H1 is given by
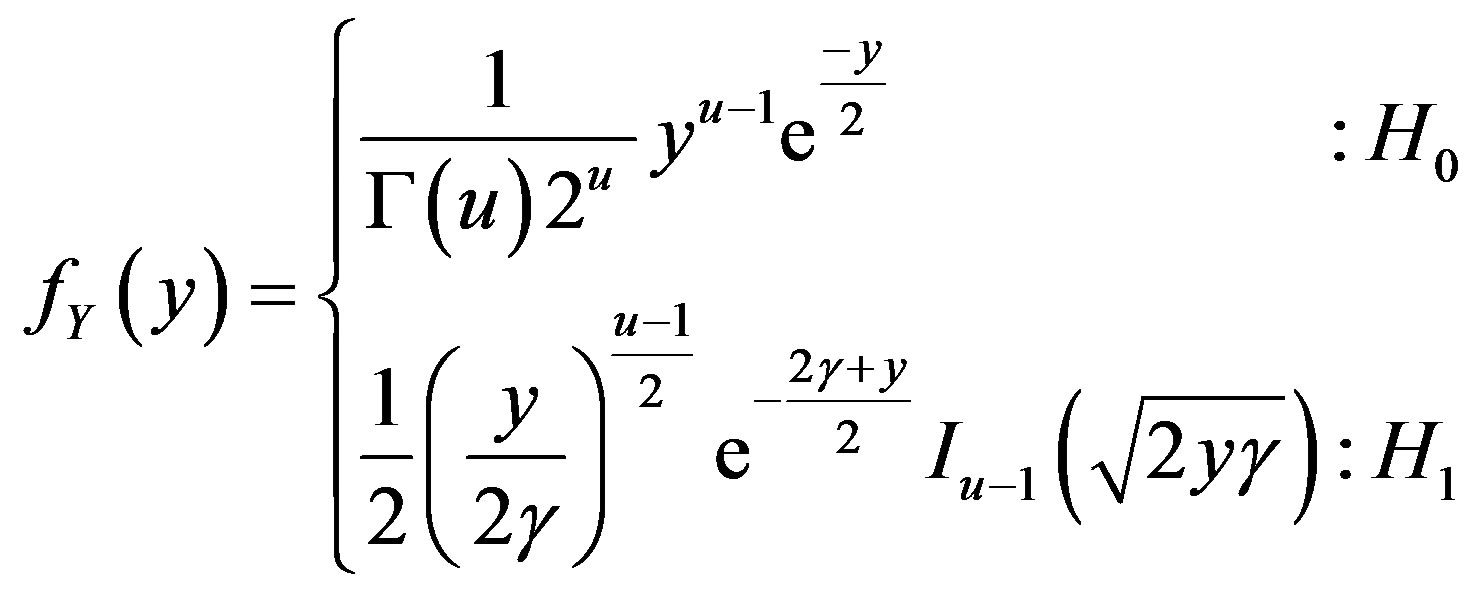 (7)
(7)
where Г(.) is the gamma function, Iv(.) is the vth order modified Bessel function of the first kind, and u = TW is the time bandwidth product.  is the signal to noise ratio at the cognitive coordinator. The detection probability (Pd) and probability of false alarm (Pf) are denoted as
is the signal to noise ratio at the cognitive coordinator. The detection probability (Pd) and probability of false alarm (Pf) are denoted as
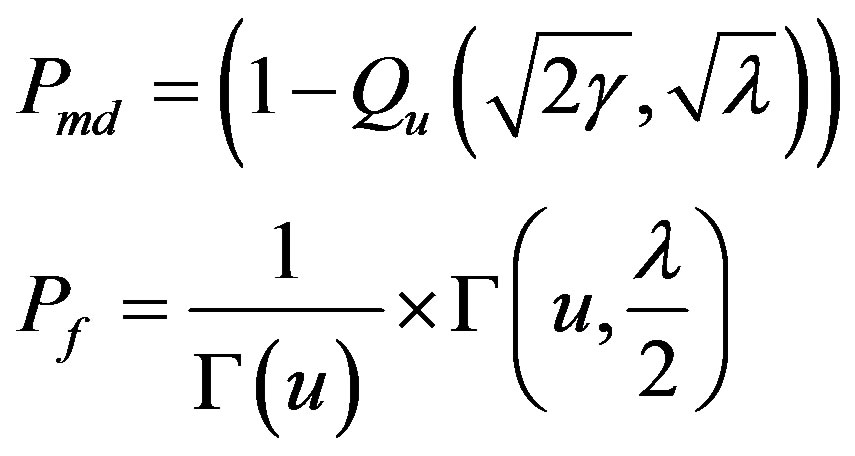 (8)
(8)
A circular contour (Ω) integral representation given by [26] in terms of Marcum-Q function with radius r can be represented as
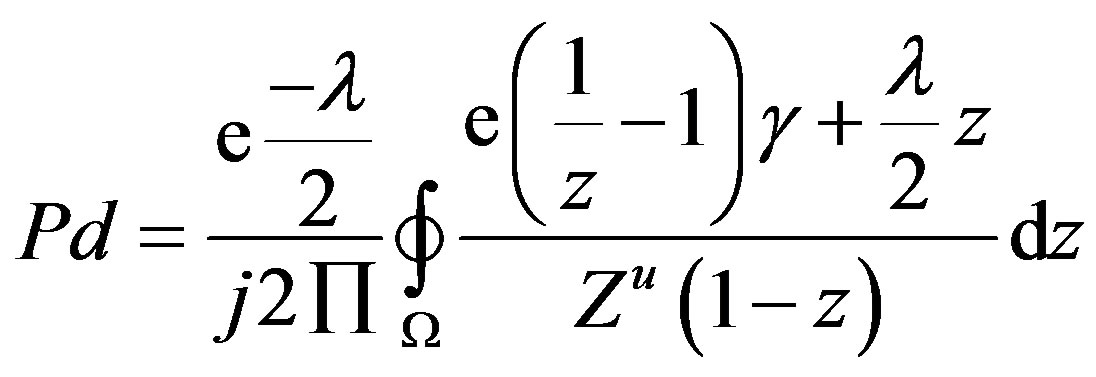 (9)
(9)
where W is the circular contour of radius r that encloses the origin. The singularities of the integrand are Z = 0 and Z = 1 therefore radius of the contour ranges from 0 to 1. The received signal’s SNR changes randomly in a faded channel; because of this the detection probability is also random in nature. So, the average detection probability Pd(Avg) is given by
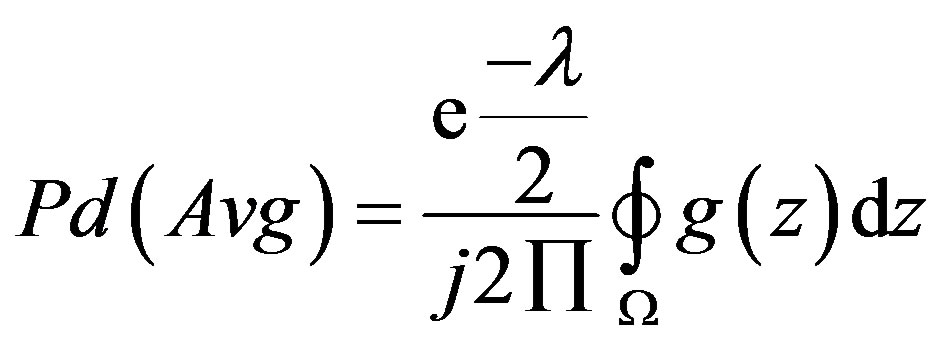 (10)
(10)
 (11)
(11)
where  is the moment generating function (MGF) of SNR
is the moment generating function (MGF) of SNR 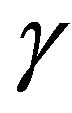 and E(.) is the expectation.
and E(.) is the expectation.
3.2. Cascaded Multihop Channel with Nakagami-m Characteristics
In cascaded multihop system, all relays are serially connected with each other. The output of first relay is the input of the second and so on. The end to end signal SNR is dependent upon individual hop SNR. The relays within a wireless link can work on the condition, which is based upon the fact that the multihop branch is dominated by the weakest SNR within the hops of relayed link. This estimation has been referred by various authors working for the recital analysis of multihop systems [27,28]. According to this approximation, the end-to-end SNR of the relayed branch is given by
 (12)
(12)
This SNRγl,  is averaged over Nakagamim PDF and can be expressed as
is averaged over Nakagamim PDF and can be expressed as
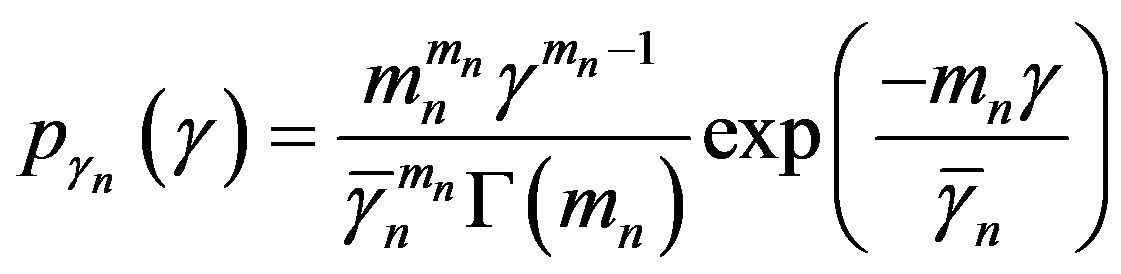 (13)
(13)
3.3. Direct Link Integration
Direct link can be established when there is LOS distance between (PU-Tx) and (PU-Rx). This direct link incorporation would have influence on the detection performance. The Pd can be improved with the association of direct link. The total SNR will now dependent upon both the links and is the summation of MGF of both links. The destination combines the received signals from the source to destination (direct link) and source to relays and then to the destination link (relay link). The combination of direct and relayed wireless links will result in improved system performance. So, for further analysis both the links has been considered.
4. Performance Evaluation Results and Discussion
In this section, the average detection probability in multihop wireless link over Nakagami-m fading channel is investigated. In the investigations, both independent and identically distributed (i.i.d) and independent and nonidentically distributed (i.n.i.d) channels for L-hops are assumed. Also, it is assumed that the link is operating in L-hops and relays are located at equal distances between (PU-S) and (PU-R), and the normalized threshold SNR is also scaled by L. Channel state information (CSI) is assumed to be available at each receiving node and all cascaded nodes within a wireless link are coordinated, i.e., transmission within whole chain occurs without any delay. Based on the system model, the simulation results are given in this section. The analysis covers the receiver operating curves (ROC). It is shown that the spectrum sensing employed in the cognitive radio network depends upon channel distributions. The results shown in this section are for average detection probability of the multihop wireless link. Each relay node act as a pseudo random bit sequence generator (PRBS). The PRBS is modulated by digital modulation techniques for the simulation. The modulated information is transmitted in the channel as symbols. Each symbol is assigned specific energy E as per the transmitted power requirements. The transmitted symbol is corrupted by (AWGN) and fading effects in the channel. The AWGN is additional to the transmitted symbol to set required 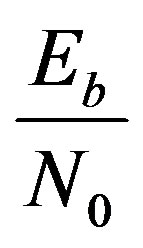 (SNR) over the wireless communication link. The symbol with SNR
(SNR) over the wireless communication link. The symbol with SNR 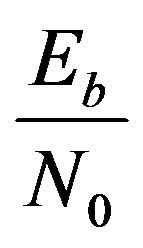
is multiplied by random Nakagami-m fading coefficients generated from the Nakagami-m distribution. Further, energy detection can be used to analyze the spectrum availability. The symbol in the channel is now faded according to the Nakagami-m fading. Nakagami-m fading with arbitrary fading parameters and arbitrary average SNR levels has been used to carry simulation through MATLAB. The AWGN can also be added to the symbol as per required SNR with the help of dedicated function. Figure 2 indicates the Pd verses Pf for four hop cascaded multihop system with different values of average SNR. As the value of average SNR within wireless link are increased, the Pd starts increasing. The interesting fact is the value of targeted Pd 0.9 is reported at average SNR of 16 dB with Nakagami-m fading severity parameter m = 2 and Pf = 0.2.
We also have analyzed the spectrum sensing with different values of fading severity parameter m. The Pd has direct relation with the severity parameter m. To explore the other side, the receiver operating curves can also be dependent upon fading severity parameter m. The practical value for m lies between 0 - 5 in typical wireless communication. We considered cascaded multihop channel consisting of L hops with desired probability of detection (0.9) and probability of false alarm (0.1 - 0.2).
Figure 3 shows, as the value of severity parameter “m” start increasing, the Pd also increasing within a three hop wireless link. The value of targeted Pd = 0.9 is reported at severity parameter m = 4 for average SNR of 12 dB at the Pf = 0.2. Further, we analyze the spectrum sensing with number of hops in cascaded multihop network.
Figure 4 represents the ROC curve in case of cascaded multi hoped Nakagami-m channel with direct link integration. The average SNR is taken as 12 dB. It is evident for m = 2, that the Pd is dependent upon the number of cascaded relays in the wireless link. Figure 4 also represents an interesting fact that if direct transmission takes place i.e. no relay (L = 0) is placed between (PU-S)
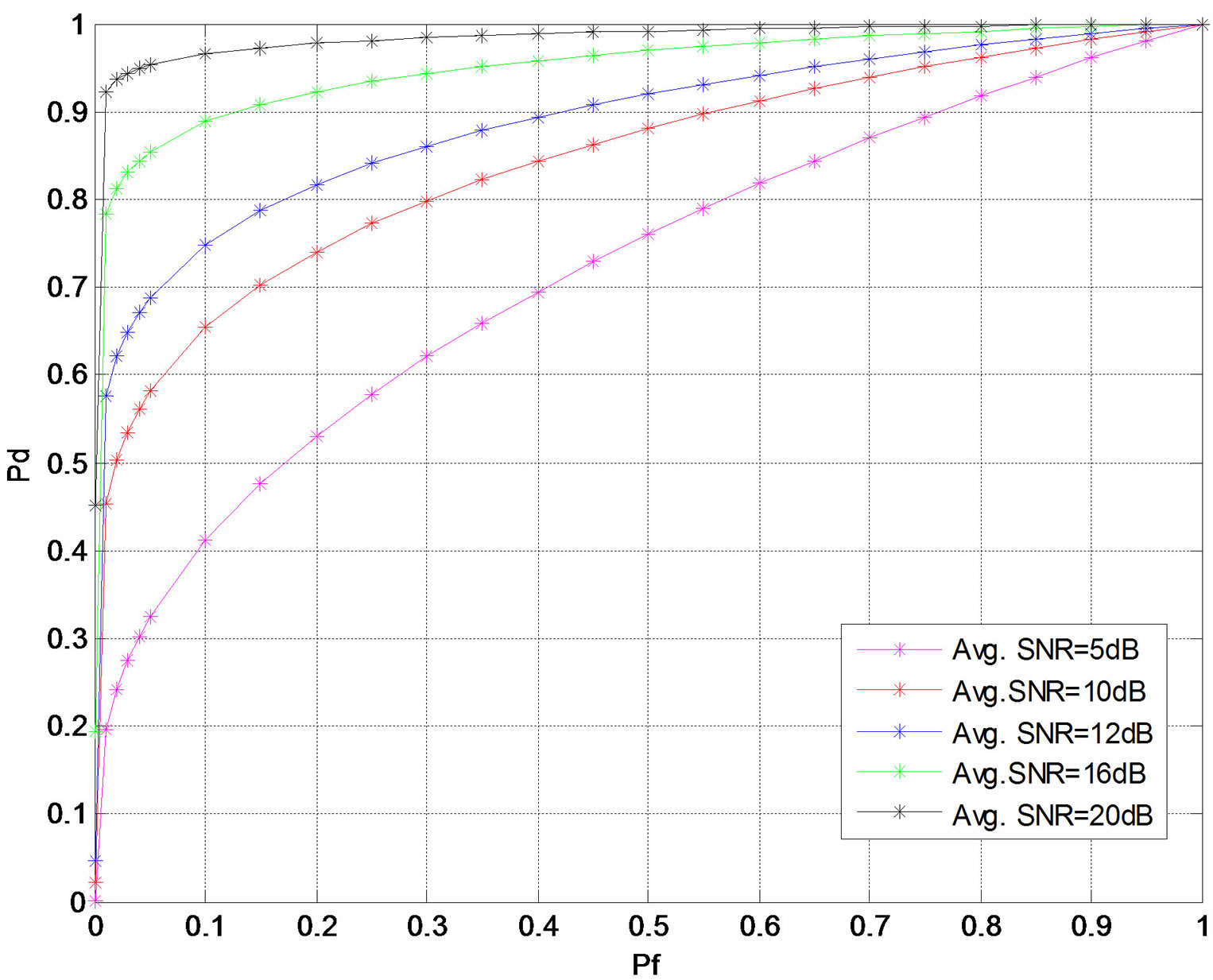
Figure 2. ROC analysis in Nakagami-m fading with different avg. SNR in four hops system.

Figure 3. ROC analysis in Nakagami-m fading with avg. SNR = 12 dB in three hop system.
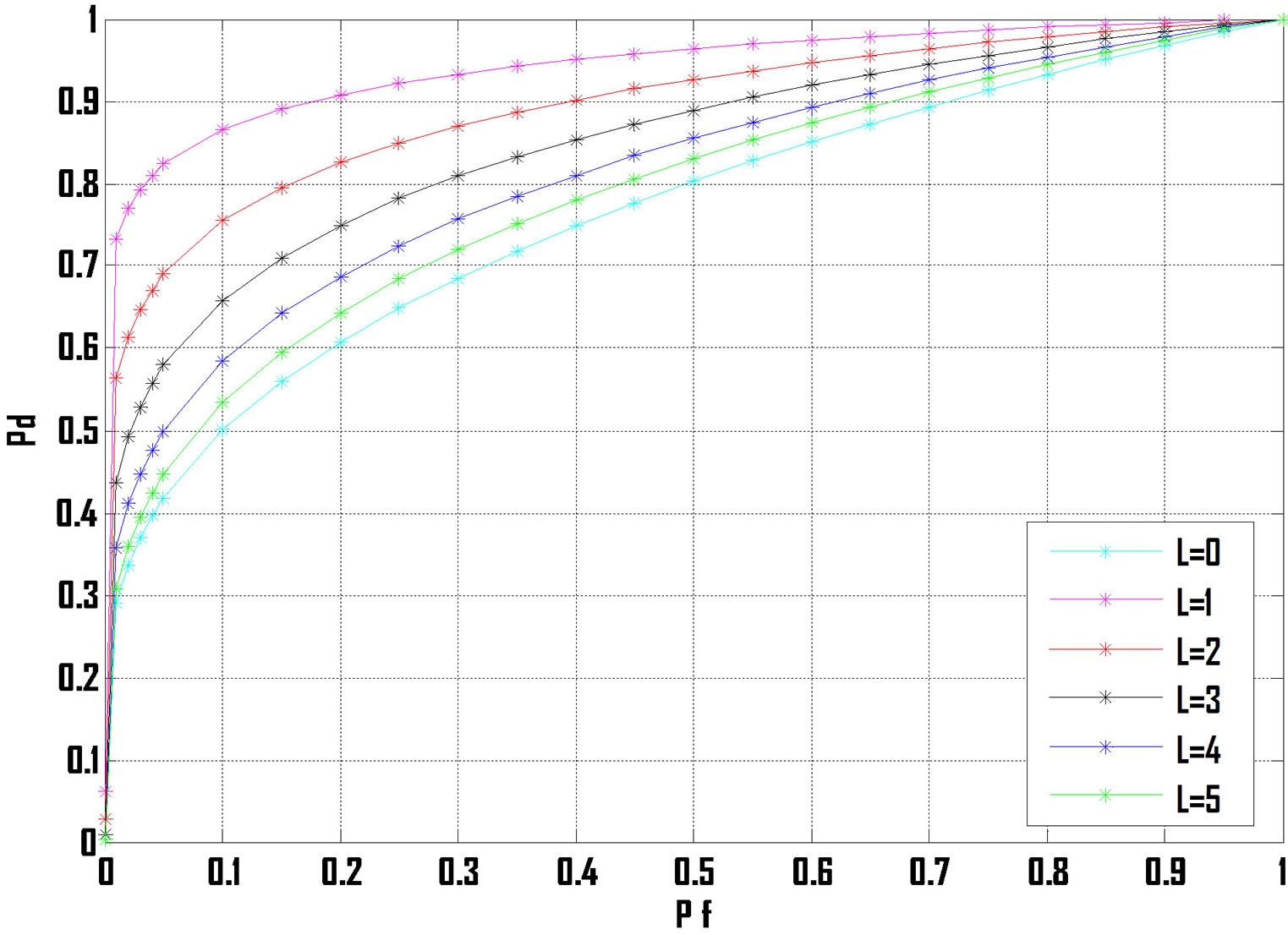
Figure 4. ROC for four-hop link for different numbers of hops and avg. SNR = 12 dB.
and (PU-D), then we get the lower bound value of 𝑃d. If one relay (L = 1) is placed between (PU-S) and (PU-D), there is an abrupt change in Pd for the fixed value of 𝑃f = 0.2. That value of Pd act as an upper bound value. The upper bound value clearly represents that the detection performance improves a lot with the incorporation of single relay between transmitter and receiver. But, it doesn’t go on increasing with increase in number of relays. As the relays within a wireless link starts increasing, the value of Pd lies in between the upper and lower bound Pd values.
Figure 5 represents the ROC curves for cascaded multihop system with 4 hops and one direct channel between (PU-S) and (PU-D). In case of i.n.i.d channels, it has been investigated that the (Pd) varies with average SNR per hop for the fixed value of m. It has been concluded that if the average SNR within the hop start increasing the Pd also increasing for a fixed value of Pf.
Figure 6 shows the comparison of three and four hop multihop cascaded model. The four hops system can outperform the three hops if the average SNR between hops of four hops network is greater than the average SNR within the hops of three hops network.
5. Conclusion
The closed form expressions for end to end SNR have been given for cascaded multihop communication link over Nakagami-m fading channels. The method presented in this contribution is useful for the Pd analysis. The performance evaluation is done by keeping three main objectives in mind i.e. number of relays, type of relays and fading severity. It is to be mentioned that the several investigations have been performed to determine the effect of increasing the number of hops on the performance of multihop network. Further, results clearly include evaluation of Pd under different channel conditions with variable m. This work carried to evaluate the
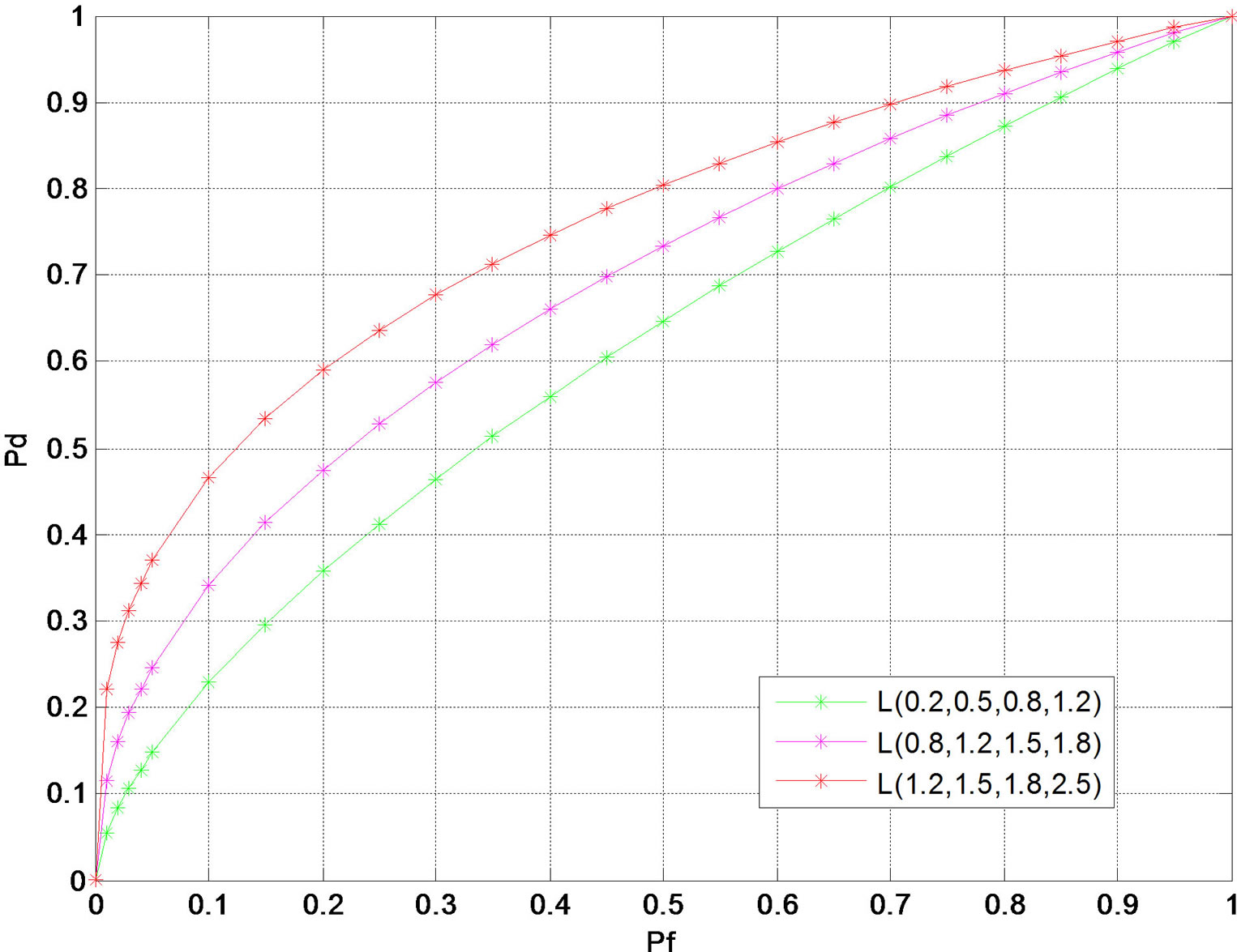
Figure 5. ROC for four-hop link for different values of avg. SNR and m = 2.
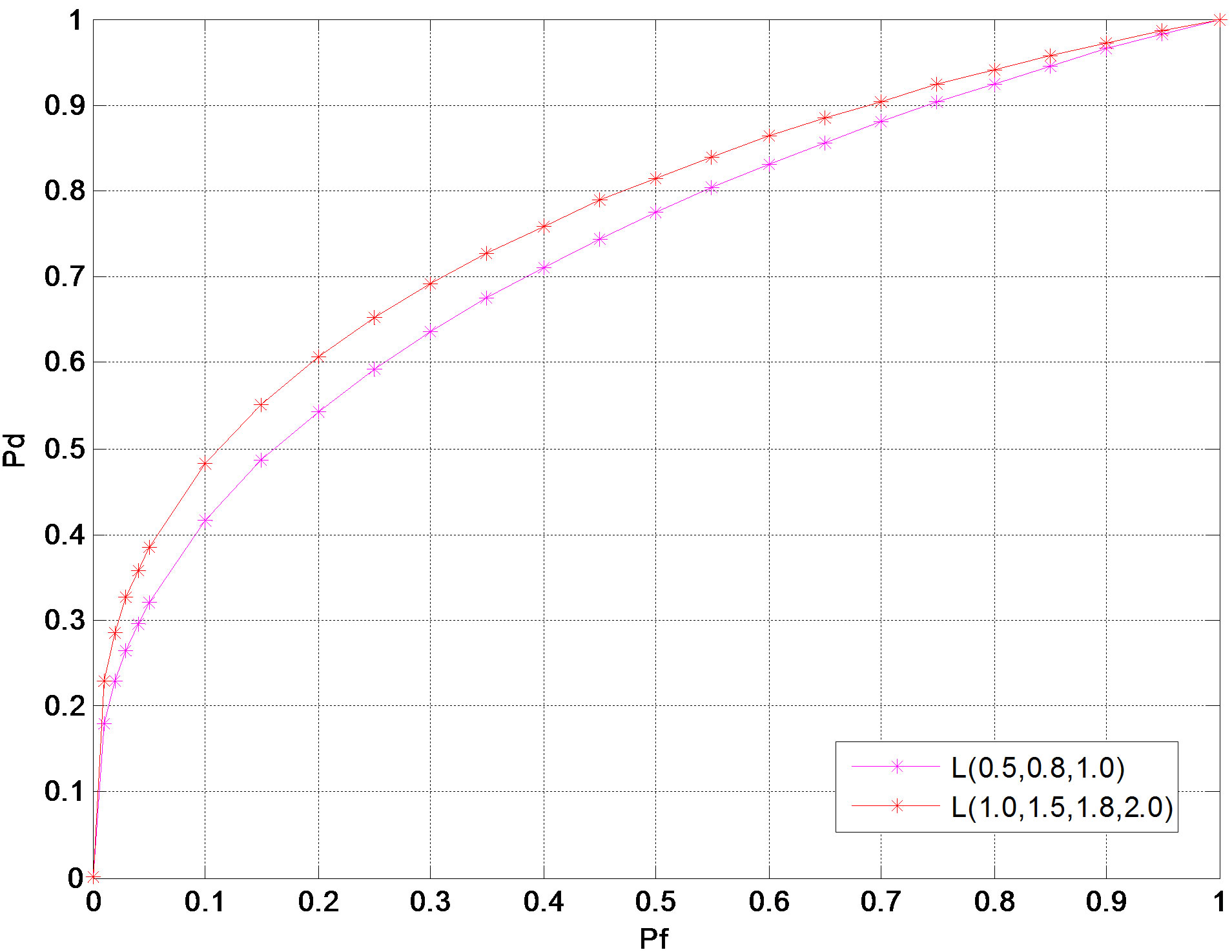
Figure 6. Comparison analysis of three and four hop cascaded model with (i.n.i.d) channels.
performance analysis of energy detection system in Nakagami-m fading channel for a cascaded multihop wireless link and has yield an optimum value of fading parameter m for the desired detection probability. Further the detection performance is improved by deploying the diversity (multi-branch) scheme. On the basis of investigation, it is to be noted that the increasing number of relays/hops deteriorates the performance of the system for the given average SNR and fading parameter m. Inspection also reveals that if the channel conditions are good, the greater number of hops can be used to achieve target Pd.
REFERENCES
- D. Cabric, S. M. Mishra and R. W. Brodersen, “Implementation Issues in Spectrum Sensing for Cognitive Radios,” Proceedings of 38th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, 7-10 November 2004, Vol. 1, pp. 772-776.
- D. Cabric, A. Tkachenko and R. Brodersen, “Spectrum Sensing Measurements of Pilot Energy and Collaborative Detection,” Proceedings of IEEE Military Communication Conference, Washington DC, 23-25 October 2006, pp. 1-7.
- G. Ganesan and Y. Li, “Agility Improvement through Cooperative Diversity in Cognitive Radio,” Proceedings of IEEE Global Telecommunications Conference (Globecom), St. Louis, Vol. 5, 28 November-2 December 2005, pp. 2505-2509.
- G. Ganesan and Y. Li, “Cooperative Spectrum Sensing in Cognitive Radio, Part I: Two User Networks,” IEEE Transactions on Wireless Communications, Vol. 6, No. 6, 2007, pp. 2204-2213. http://dx.doi.org/10.1109/TWC.2007.05775
- H. Urkowitz, “Energy Detection of Unknown Deterministic Signals,” Proceedings of IEEE, Vol. 55, No. 4, 1967, pp. 523-531. http://dx.doi.org/10.1109/PROC.1967.5573
- G. Ganesan and Y. Li, “Cooperative Spectrum Sensing in Cognitive Radio, Part II: Multiuser Networks,” IEEE Transaction on Wireless Communications, Vol. 6, No. 6, 2007, pp. 2214-2222. http://dx.doi.org/10.1109/TWC.2007.05776
- R. Fan and H. Jiang, “Optimal Multi-Channel Cooperative Sensing in Cognitive Radio Networks,” IEEE Transaction on Wireless Communications, Vol. 9, No. 3, 2010, pp. 1128-1138. http://dx.doi.org/10.1109/TWC.2010.03.090467
- W. Zhang and K. B. Letaif, “Cooperative Communications for Cognitive Radio Networks,” Proceedings of the IEEE, Vol. 97, No. 5, 2009, pp. 878-893. http://dx.doi.org/10.1109/JPROC.2009.2015716
- F. F. Digham, M. S. Alouini and M. K. Simon, “On the Energy Detection of Unknown Signals over Fading Channels,” IEEE Transaction on Wireless Communication, Vol. 55, No. 1, 2007, pp. 21-24.
- A. Ghasemi and E. S. Sousa, “Collaborative Spectrum Sensing for Opportunistic Access in Fading Environments,” Proceedings of the IEEE Dynamic Spectrum Access Networks, Baltimore, 8-11 November 2005, pp. 131-136.
- J. Shen, T. Jiang, S. Liu and Z. Zhang, “Maximum Channel throughput via Cooperative Spectrum Sensing in Cognitive Radio Networks,” IEEE Transaction on Wireless Communication, Vol. 8, No. 10, 2009, pp. 5166-5175. http://dx.doi.org/10.1109/TWC.2009.081110
- S. M. Mishra, A. Sahai and R. W. Brodersen, “Cooperative Sensing among Cognitive Radios,” Proceeding of IEEE International Conference on Communication, Istanbul, 11-15 June 2006, pp. 1658-1663.
- S. Atapattu, C. Tellambura and H. Jiang, “Energy Detection Based Cooperative Spectrum Sensing in Cognitive Radio Networks,” IEEE Transactions on Wireless Communications, Vol. 10, No. 4, 2011, pp. 1232-1241. http://dx.doi.org/10.1109/TWC.2011.012411.100611
- H. Khalif, N. Malouch and S. Fdida, “Multihop Cognitive Radio Network: To Route or Not to Route,” IEEE Network, Vol. 23, No. 4, 2009, pp. 20-25. http://dx.doi.org/10.1109/MNET.2009.5191142
- Y. Yuan, P. Bhal, R. Chandra, P. Chou, J. Ferrell, T. Moscibroda, S. Narlanka and Y. Wu, “KNOWS: Cognitive Networking over White Spaces,” Proceedings of 2nd IEEE DySPAN, Dublin, 17-20 April 2007, pp. 416-427.
- J. Jia, Q. Zhang and X. Shen, “HC_MAC: A HardwareConstrained Cognitive MAC for Efficient Spectrum Management,” IEEE Journal on Selected Areas in Communications, Vol. 26, No. 1, 2008, pp. 106-117. http://dx.doi.org/10.1109/JSAC.2008.080110
- V. Ashgari, D. B. da-Costa and S. Aissa, “Performance Analysis of Multihop Relaying Channels with Nakagami-m Fading: Ergodic Capacity Upper-Bounds and Outage Probability,” IEEE Transaction on Communication, Vol. 60, No. 10, 2012, pp. 2761-2767. http://dx.doi.org/10.1109/TCOMM.2012.081012.100156
- E. Morgado, I. Mora-Jimenez, J. J. Vinagre, J. Ramos and A. J. Caamano, “End-to-End Average BER in Multihop Wireless Networks over Fading Channels,” IEEE Transaction on Wireless Communication, Vol. 9, No. 8, 2010, pp. 2478-2487. http://dx.doi.org/10.1109/TWC.2010.070710.090240
- N. C. Beaulieu and J. Hu, “A Closed-Form Expression for the Outage Probability of Decode-and-Forward Relaying in Dissimilar Rayleigh Fading Channels,” IEEE Communication Letter, Vol. 10, No. 12, 2006,pp. 813-815. http://dx.doi.org/10.1109/LCOMM.2006.061048
- G. K. Karagiannidis, T. A. Tsiftsis and R. A. Mallik, “Bounds for Multihop Relayed Communications in Nakagami-m Fading,” IEEE Transactions on Communications, Vol. 54, No. 1, 2006, pp. 18-22. http://dx.doi.org/10.1109/TCOMM.2005.861679
- H. A. Suraweera and G. K. Karagiannidis, “Closed-Form Error Analysis of the Non-Identical Nakagami-m Relay Fading Channel,” IEEE Communications Letters, Vol. 12, No. 4, 2008, pp. 259-261. http://dx.doi.org/10.1109/LCOMM.2008.071922
- H. A. Suraweera, D. S. Michalopoulos and G. K. Karagiannidis, “Performance of Distributed Diversity Systems with a Single Amplify-and-Forward Relay,” IEEE Transactions on Vehicular Technology, Vol. 58, No. 5, 2009, pp. 2603-2608. http://dx.doi.org/10.1109/TVT.2008.2007798
- N. C. Beaulieu and C. Cheng, “Efficient Nakagami-m Fading Channel Simulation,” IEEE Transaction on Vehicular Technology, Vol. 54, No. 2, 2005, pp. 413-424. http://dx.doi.org/10.1109/TVT.2004.841555
- M. O. Hasna and M. S. Alouini, “A Performance Study of Dual-Hop Transmissions with Fixed Gain Relays,” IEEE Transactions on Wireless Communications, Vol. 3, No. 6, 2004, pp. 1963-1968. http://dx.doi.org/10.1109/TWC.2004.837470
- Y. L. Zou, J. Zhu, B. Y. Zheng and Y.-D. Yao, “An Adaptive Cooperation Diversity Scheme with Best-Relay Selection in Cognitive Radio Networks,” IEEE Transactions on Signal Processing, Vol. 58, No. 10, 2010, pp. 5438- 5445. http://dx.doi.org/10.1109/TSP.2010.2053708
- C. Tellambura, A. Annamalai and V. K. Bhargva, “Contour Integral Representation for Generalized Marcum-Q Function and Its Application to Unified Analysis of DualBranch Selection Diversity over Correlated Nakagami-m Fading Channels,” Proceeding of the 51st IEEE Vehicular Technology Conference, Tokyo, 15-18 May 2000, Vol. 2, pp. 1031-1034.
- S. Ikki and M. H. Ahmed, “Performance Analysis of Cooperative Diversity Wireless Networks over Nakagami-m Fading Channel,” IEEE Communications Letters, Vol. 11, No. 4, 2007, pp. 334-336. http://dx.doi.org/10.1109/LCOM.2007.348292
- T. Wang, A. Cano, G. B. Giannakis and J. N. Laneman, “High Performance Cooperative Demodulation with Decode-and-Forward Relays,” IEEE Transaction on Communication, Vol. 55, No. 4, 2007, pp. 1427-1438. http://dx.doi.org/10.1109/TCOMM.2007.900631

