Engineering
Vol. 5 No. 1 (2013) , Article ID: 26394 , 6 pages DOI:10.4236/eng.2013.51003
Study on Thin Layer Drying of Rosa laevigata Michx
1College of Life Science, Guizhou University, Guiyang, China
2Research and Development Center of Traditional Chinese Medicinal and Natural Products, Guizhou University, Guiyang, China
3Guizhou Engineering Laboratory of Propagation and Cultivation on Traditional Chinese Medicinal Materials, Guiyang, China
Email: sci.blin@gzu.edu.cn
Received September 22, 2012; revised October 30, 2012; accepted November 15, 2012
Keywords: Drying; Mathematical Modelling; Kinetics; Rosa laevigata Michx
ABSTRACT
The drying process of traditional Chinese medicine Rosa laevigata Michx was investigated in a laboratory scale dryer. Drying experiments were conducted at five temperatures of 40˚C, 50˚C, 60˚C, 70˚C and 80˚C. The experimental data were fitted to ten different thin layer drying models to select a suitable model for describing the drying process of Rosa laevigata Michx fruits. The results showed that the Midilli model had the highest value of R2 (0.999767), the lowest χ2 (0.000034) and RMSE (0.003616) among the ten models considered. The drying process of Rosa laevigata Michx fruits consisted of 1st falling rate period and 2nd falling rate period. The effective moisture diffusivity was found in the range of 1.49 - 30.20 × 10−11 m2·s−1. The value of activation energy obtained by plotting lnD versus 1/T is about 36 kJ·mol−1.
1. Introduction
It is well known that traditional Chinese medicine (TCM) has been used in the therapy of many diseases for several thousand years in China and neighbor countries and plays a more and more important role in modern pharmaceutical industry. In the process of refining TCM, drying is the most important methods and the oldest ways to remove the moisture in the solid. The main objective in drying herbal medicine is to minimize biochemical, chemical and microbiological deterioration of herbal medicine due to the reduction of the moisture content to a certain level, which allows safe storage over a long period and bring substantial reduction in weight and volume, minimizing packaging, storage and transportation costs [1]. Moisture content of TCM should be controlled under safe level according to Chinese Pharmacopoeia. Rosa laevigata Michx, an evergreen climbing shrub widely distributed throughout southern China, is a member of the Rosaceae family. The fruit of this plant is widely used as a traditional Chinese folk medicine and also used as a foodstuff in the traditional brewing of wine, as well as for the extraction of brown pigments used as food additives. In addition, Rosa laevigata Michx fruits are prescribed in the Chinese Pharmacopoeia for the treatment of wet dreams, urinary incontinence, urinary frequency, uterine prolapse, menstrual irregularities and leucorrhea [2]. Rosa laevigata Michx fruits contains polysaccharide, organic acid, tannins, triterpene, vitamin C and other components [3]. Polysaccharide is the main component and is used as quality assessment criteria, no less than 25% (w/w) according to Chinese pharmacopoeia [4]. There are two harvest periods for Rosa laevigata Michx fruits: the first is when it is ripe (usually from October to December), and the second is when it is partly yellow but not yet ripe (usually from August to September) [3].
Growing attentions have been paid to pharmacological effect of Rosa laevigata Michx on curing hyperpiesia, chronic cough, and dermatogic disease etc. [5]. However, systematic studies on the drying process of Rosa laevigata Michx fruits was not found as far as we known. So far, most of methods for drying TCM, which usually leads to high energy-consuming, time-consuming and degradation of biochemical active component, are empirical. In order to reduce energy consumption, save time and avoid degradation of biochemical active component, the drying model of TCM needs to be established by experimentation and verified by comparing simulated values with experimental data. The principle of modeling is based on having a set of mathematical equations that can adequately describe the system. The solution of these equations must allow prediction of parameters, such as moisture content, energy consumption etc., as a function of time at any point in the dryer based only on the initial conditions. Therefore the use of a simulation model is a valuable tool for prediction of drying time and optimization of dryers [6]. The aim of this work is to 1) evaluate the suitability of the drying models widely used to describe agricultural products for the drying process of traditional Chinese medicine; 2) study the drying kinetics and determine the moisture diffusivity and activation energy during drying of Rosa laevigata Michx fruits.
2. Materials and Methods
2.1. Samples Preparation
Fresh Rosa laevigata Michx fruits were collected from Guiyang, Guizhou Province, China, in November 2011. Then the fruits were cleaned and stored in a refrigerator at 4˚C ± 1˚C. At the start of each experiment, the fruits were hemisected and separated from the seeds according to Chinese Pharmacopoeia.
2.2. Instruments
The drying experiments were carried out using a laboratory dryer (DGG-9246A type, Shanghai Keelrein Instrument Co. Ltd.) in technical center of Guizhou University & Guizhou Bailing Group Pharmaceutical Company Limited. The dryer had an automatic temperature controller and is capable of providing any desired drying air temperature in the range of RT (room temperature) +10 to 300˚C with an accuracy of ±0.1˚C. The temperature and relative humidity of the room where the dryer was installed was about 10˚C - 20˚C and 40% - 65% respectively. Prior to placing the sample into the drying chamber, the system had been running for at least 0.5 h to obtain steady conditions.
The moisture content (dry basis, kg water/kg solids) of the Rosa laevigata Michx fruits was measured by Mettler Toledo HR83 halogen moisture analyzer. The halogen moisture analyzer provides fast and reproducible results with repeatability of 0.05% (2 g sample) moisture content. The temperature range that the halogen moisture analyzer provided is between 40˚C to 200˚C. Substances which subject to infrared ray with very low moisture content (10 ppm) can be analyzed by this instrument.
2.3. Drying Experiments
The drying experiments were conducted at five temperatures of 40˚C, 50˚C, 60˚C, 70˚C and 80˚C. About 120 g of Rosa laevigata Michx fruits were uniformly spread in a tray and kept inside the dryer. About 15 g fruits were taken out of the dryer at each suitable interval and then grinded to powder by an electric grinder. The moisture content of the fruits powder was measured by the halogen moisture analyzer at 105˚C with standard temperature program. Each drying experiment was repeated three times.
3. Mathematical Modeling
The moisture ratio (MR) of Rosa laevigata Michx fruits during experiments was calculated by the following equation:
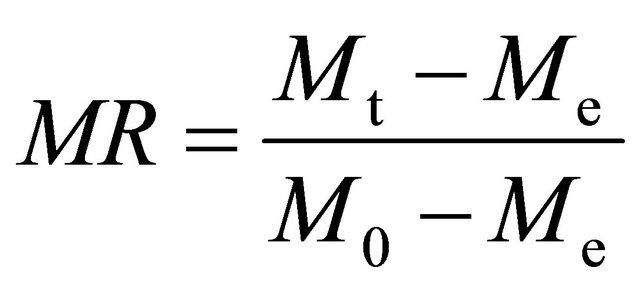 (1)
(1)
where Mt is the moisture content at time t, M0 and Me are the initial and equilibrium moisture contents, respectively, on dry basis. Since the values of Me are relatively little, Equation (1) can be simplified as [6]:
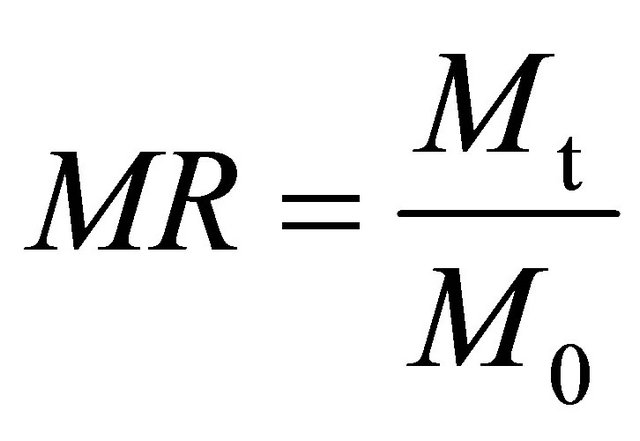 (2)
(2)
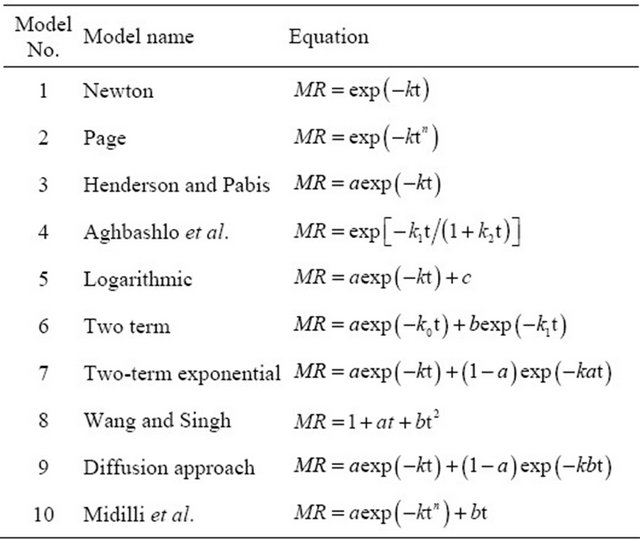
To select a suitable model for describing the drying process of Rosa laevigata Michx fruits, drying curves were fitted to ten well known thin layer drying models [7-13] which are presented in Table 1.
The non-linear regression analysis was done using IBM SPSS version 19.0. Three parameters, coefficient of determination (R2), reduced chi-square (χ2) and root mean square error (RMSE) were used as criteria to select the best equation to account for drying curves. These statistical values can be calculated as follows [6,12]:
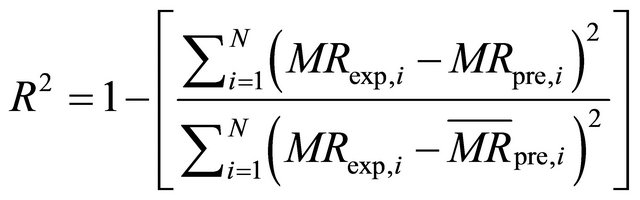 (3)
(3)
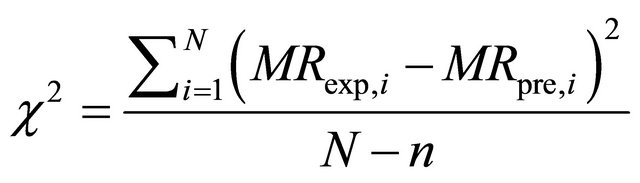 (4)
(4)
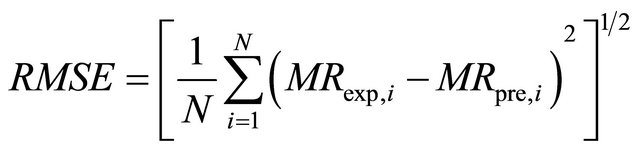 (5)
(5)
where MRexp,i is the ith experimental moisture ratio, MRpre,i is the ith predicted moisture ratio, N is the number of observations and n is the number of parameters in the equations that has been used. The best model describing the thin layer drying characteristics of Rosa laevigata Michx was chosen as the one with the highest R2-value and the lowest RMSE and χ2-values.
Since the thickness of hemisected fruits of Rosa laevigata Michx was about 2 mm, the equation of Fick’s second law was used for calculation of effective moisture diffusivity of drying process. Fick’s diffusion equation was expressed as follows [6]:
 (6)
(6)
where 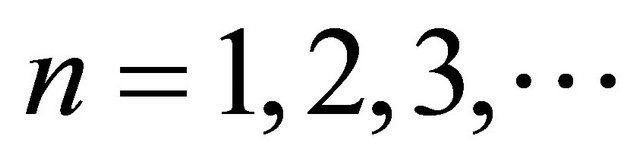 the number of terms taken into consideration, t is the time of drying (s), D is effective moisture diffusivity (m2·s−1) and L is the thickness of slice (m). Only the first term of Equation (6) is used for long time drying [14]:
the number of terms taken into consideration, t is the time of drying (s), D is effective moisture diffusivity (m2·s−1) and L is the thickness of slice (m). Only the first term of Equation (6) is used for long time drying [14]:
Table 1. Thin layer drying models applied to drying curves.
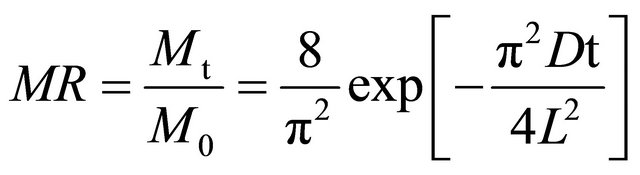 (7)
(7)
Taking the natural logarithm on both sides of Equation (7) yields:
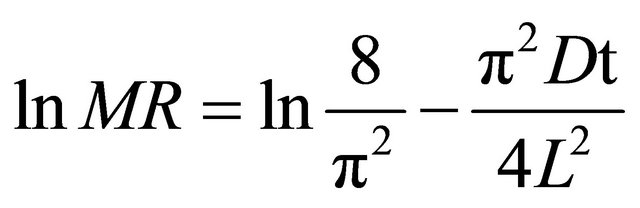 (8)
(8)
According to Equation (8), a straight line can be obtained by plotting lnMR versus t. Thus, the effective moisture diffusivity D can be determined from the slope. The relationship between effective moisture diffusivity D and temperature is represented by an Arrhenius type equation [14]:
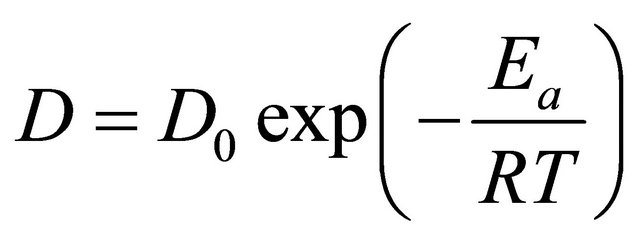 (9)
(9)
where D0 is the pre-exponential factor of the Arrhenius equation (m2·s−1), Ea is the activation energy (kJ·mol−1), R is universal gas constant (8.314 kJ·mol−1·K–1) and T is absolute temperature (K). Equation (9) can be linearized by taking natural logarithm on both sides:
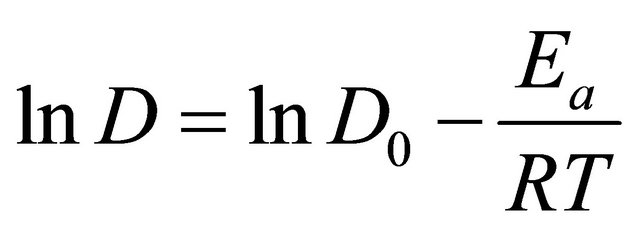 (10)
(10)
The activation energy can be calculated from the slope of the plot lnD versus 1/T.
4. Results and Discussion
The initial moisture content of the raw fruits was 193.00 ± 2.05 kg/kg (dry basis). The drying curves of Rosa laevigata Michx fruits at 40˚C, 50˚C, 60˚C, 70˚C and 80˚C are shown in Figure 1.
The final moisture content of Rosa laevigata Michx fruits ranged from 5.72% to 10.85% (dry basis). As can
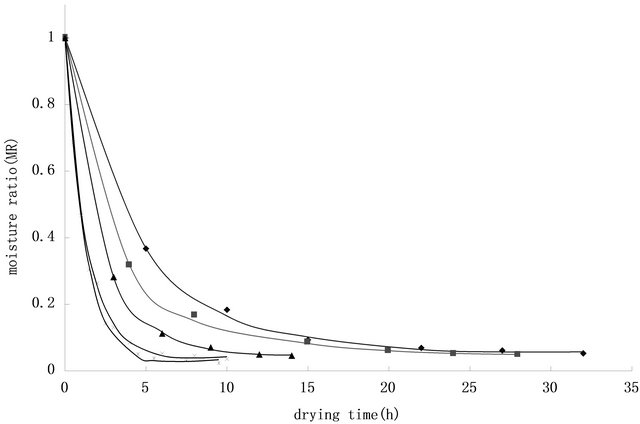
Figure 1. Drying curves of Rosa laevigata Michx fruits at 40˚C, 50˚C, 60˚C, 70˚C and 80˚C. Experimental data and values calculated by the new model. Experimental: ◆: 40˚C; ■: 50˚C; ▲: 60˚C; ×: 70˚C; *: 80˚C. Simulated: (a) 40˚C; (b) 50˚C; (c) 60˚C; (d) 70˚C; (e) 80˚C.
be seen from Figure 1, the moisture ratios during the drying decreased exponentially as the drying time increased. It was evident that drying temperature significantly affected the drying process. The drying time reduced when the temperature increased. In another word, the drying rate increased with the increase in drying temperature.
The average moisture ratio of Rosa laevigata Michx fruits dried at different temperatures was fitted to ten different drying models. The statistical results from ten models are given in Table 2.
It was seen from Table 2. that the values of R2 for the Aghbashlo model, Logarithmic model, Two term model, Diffusion approach model and Midilli model were greater than 0.999, indicating good fit. The Midilli model gave the highest value of R2 = 0.999767, the lowest value of χ2 = 0.000034 and RMSE = 0.003616. Thus the Midilli model was comparatively the better drying model to represent the drying process of Rosa laevigata Michx fruits. Figure 1 was the comparison of experimental MR and simulated MR obtained by the Midilli model versus drying time under different drying temperature, which indicated a good fit.
Based on Equation (8), the plots of lnMR versus drying time t at different temperatures were shown in Figure 2.
As can be seen from Figure 2, the constant rate period was absent, and the drying process of Rosa laevigata Michx fruits at different temperatures consisted of two regions, 1st falling rate period of drying and 2nd falling rate period of drying, having different slopes. The critical moisture content represents of the time when the surface was completely dried and moisture was transported from inside of the fruits to the surface by capillary action [15]. Similar situation were observed by C. T. Akanbi [16], and T. Arumuganathan [12] etc. The best-fit regression
Table 2. Statistical results of the drying model.
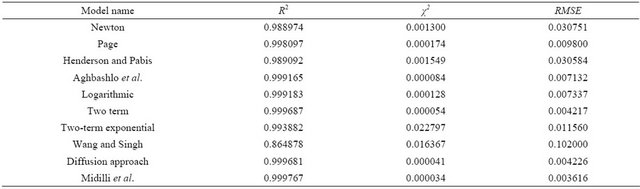
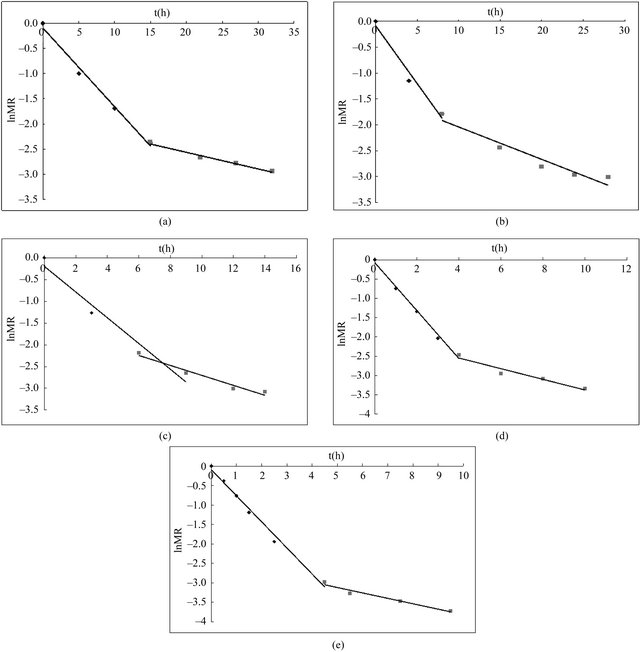
Figure 2. The plots of lnMR versus drying time t for drying of Rosa laevigata Michx fruits at temperatures. (a) 40˚C; (b) 50˚C; (c) 60˚C; (d) 70˚C and (e) 80˚C.
equations at different temperature during first and second falling rate periods of drying were given in Table 3.
It was found that during the first and second falling rate periods the absolute values of slop of regression lines were increased with the increase of temperature. The values of first and second effective moisture diffusivity D at different temperatures were calculated from the slops of regression lines according to Equation (8) and listed in Table 4.
It was observed from Table 4, as expected, the drying temperature affect the values of D greatly. Effective moisture diffusivity values of first and second falling rate increase with the increase in drying temperature. These values were within the general range of 10–9 - 10–11 m2·s−1 for agricultural products [17]. Two straight lines were obtained by plotting lnD versus 1/T with correlation coefficient R2 0.9672 and 0.9300 respectively (Figure 3). Therefore, the values of activation energy could be calculated from the slope of the straight lines (also listed in Table 4).
Figue 3 showed the variation of activation energy of 1st falling rate period and that of 2nd falling rate period was small. The effect of temperature on Effective moisture diffusivity during 1st falling rate period was consistent with that during 2nd falling rate period. The value of activation energy obtained was about 36 kJ/mol which was in the general range of 12.7 - 110 kJ·mol−1 for agricultural products [18].
5. Conclusion
Mathematical modelling of the drying process was used to agricultural products widely [7,9-13], but not yet for traditional Chinese medicine. In this work, the drying process of Rosa laevigata Michx fruits was studied. The results of model simulation indicated the Midilli model gave the best results and showed good agreement with the experimental values of drying of Rosa laevigata Michx fruits. The values of drying kinetics parameters effective moisture diffusivity D and activation energy Ea which obtained through Fick’s second law and Arrhenius equation were within the general range of 10−9 - 10−11 m2·s−1 and 12.7 - 110 kJ·mol−1 respectively. Hence, mathematical modelling could be an effective tool for the
Table 3. Regression equations and correlation coefficients of 1st and 2nd falling rate of drying.
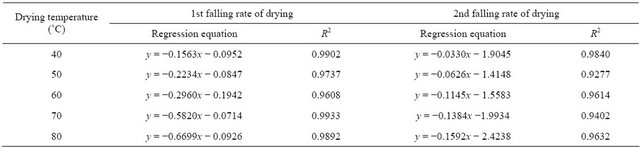
Table 4. Effective moisture diffusivity D and activation energy Ea for drying of Rosa laevigata Michx.

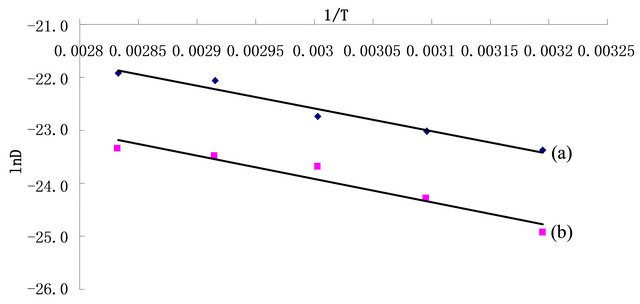
Figure 3. The plots of lnD versus 1/T for drying of Rosa laevigata Michx fruits. (a) 1st falling rate; (b) 2nd falling rate.
study of drying behavior of traditional Chinese medicine. The suitability of mathematical modelling for the drying process of other traditional Chinese medicine should be study in other works.
6. Acknowledgements
The authors would like to acknowledgment the financial support from the UIRP (Undergraduate Innovative Research Project, Guizhou University, No. (2011) 057).
REFERENCES
- M. Zielinska and M. Markowski, “Air Drying Characteristics and Moisture Diffusivity of Carrots,” Chemical Engineering and Processing: Process Intensification, Vol. 49, No. 2, 2010, pp. 212-218. doi:10.1016/j.cep.2009.12.005
- P. Y. Gao, L. Z. Li, Y. Peng, S. J. Piao, N. Zeng, H. W. Lin and S. J Song, “Triterpenes from Fruits of Rosa laevigata,” Biochemical Systematics and Ecology, Vol. 38, No. 3, 2010, pp. 457-459. doi:10.1016/j.bse.2010.03.014
- H. Yan, B. X. Han, Q. Y. Wu, M. Z. Jiang and Z. Z. Gui, “Rapid Detection of Rosa laevigata Polysaccharide Content by Near-Infrared Spectroscopy,” Spectrochimica Acta Part A, Vol. 79, No. 1, 2011, pp. 179-184. doi:10.1016/j.saa.2011.02.032
- National Pharmacopoeia Committee, “Chinese Pharmacopoeia,” Chemical Industry Press, Beijing, 2010.
- Y. T Liu., B. N. Lu and J. Y Peng, “Hepatoprotective Activity of the Total Flavonoids from Rosa laevigata Michx Fruit in Mice Treated by Paracetamol,” Food Chemistry, Vol. 125, No. 2, 2011, pp. 719-725. doi:10.1016/j.foodchem.2010.09.080
- A. Taheri-Garavand, S. Rafiee and A. Keyhani, “Study on Effective Moisture Diffusivity, Activation Energy and Mathematical Modeling of Thin Layer Drying Kinetics of Bell Pepper,” Australian Journal of Crop Science, Vol. 5, No. 2, 2011, pp. 128-131.
- O. Yaldỳ and C. Ertekỳn, “Thin Layer Solar Drying of Some Vegetables,” Drying Technology, Vol. 19, No. 3-4, 2001, pp. 583-597.
- A. Midilli, H. Kucuk and Z. Yapar, “A New Model for Single-Layer Drying,” Drying Technology, Vol. 20, No. 7, 2002, pp. 1503-1513.
- S. Simal, A. Femenia, M. C. Garau and C. Rossellό, “Use of Exponential, Page’s and Diffusional Models to Simulate the Drying Kinetics of Kiwi Fruit,” Journal of Food Engineering, Vol. 66, No. 3, 2005, pp. 323-328. doi:10.1016/j.jfoodeng.2004.03.025
- J. M. F. Faustino, M. J. Barroca and R. P. F. Guiné, “Study of the Drying Kinetics of Green Bell Pepper and Chemical Characterization,” Food and Bioproducts Processing, Vol. 85, No. 3, 2007, pp. 163-170.
- A. Vega, P. Fito, A. Andrés and R. Lemus, “Mathmatical Modeling of Hot-Air Drying Kinetics of Red Bell Pepper (Var. Lamuyo),” Journal of Food Engineering, Vol. 79, No. 4, 2007, pp. 1460-1466. doi:10.1016/j.jfoodeng.2006.04.028
- T. Arumuganathan, M. R. Manikantan, R. D. Rai, S. Anandakumar and V. Khare, “Mathematical Modeling of Drying Kinetics of Milky Mushroom in a Fluidized Bed Dryer,” International Agrophysics, Vol. 23, No. 1, 2009, pp. 1-7.
- E. Meisami-asl, S. Rafiee, A. keyhani and A. Tabatabaeefar, “Determination of Suitable Thin Layer Drying Curve Model for Apple Slices (Variety-Golab),” Plant Omics, Vol. 3, 2010, pp. 103-108.
- A. Lopez, A. Iguaz, A. Esnozand and P. Virseda, “ThinLayer Drying Behavior of Vegetable Waste from Wholesale Market,” Drying Technology, Vol. 18, No. 4-5, 2000, pp. 995-1006.
- F. Karimi, “Applications of Superheated Steam for the Drying of Food Products,” International Agrophysics, Vol. 24, No. 2, 2010, pp. 195-204.
- C. T. Akanbi, R. S. Adeyemi and A. Ojo, “Drying Characteristics and Sorption Isotherm of Tomato Slices,” Journal of Food Engineering, Vol. 73, No. 2, 2006, pp. 157-163. doi:10.1016/j.jfoodeng.2005.01.015
- A. Maskan, S. Kaya and M. Maskan, “Hot Air and Sun Drying of Grape Leather (Pestil),” Journal of Food Engineering, Vol. 54, No. 1, 2002, pp. 81-88. doi:10.1016/S0260-8774(01)00188-1
- S. J. Babalis and V. G. Belessiotis, “Influence of the Drying Conditions on the Drying Constants and Moisture Diffusivity during the Thin-Layer Drying of Figs,” Journal of Food Engineering, Vol. 65, No. 3, 2004, pp. 449- 458. doi:10.1016/j.jfoodeng.2004.02.005

