Engineering
Vol. 3 No. 10 (2011) , Article ID: 8079 , 6 pages DOI:10.4236/eng.2011.310122
Structural Reanalysis of Dynamic Systems Using Model Updating Method
Super Long Span Bridge R&D Center, Expressway and Transportation Research Institute, Korea Expressway Corporation, Gyeonggi-Do, Korea
E-mail: pcster@ex.co.kr
Received July 7, 2011; revised August 24, 2011; accepted September 1, 2011
Keywords: Model Updating, Reanalysis, Frequency Response Functions, Transformation Matrix, Damping Matrix
ABSTRACT
Model updating methodologies are invariably successful when used on noise-free simul-ated data, but tend to be unpredictable when presented with real experimental data that are unavoidably corrupted with uncorrelated noise content. In this paper, reanalysis using frequency response functions for correlating and updating dynamic systems is presented. A transformation matrix is obtained from the relationship between the complex and the normal frequency response functions of a structure. The transformation matrix is employ-ed to calculate the modified damping matrix of the system. The modified mass and stiff-ness matrices are identified from the normal frequency response functions by using the least squares method. A numerical example is employed to illustrate the applicability of the proposed method. The result indicates that the present method is effective.
1. Introduction
Model updating is a very active research field, in which significant efforts has been invested in recent years. In case some different structure should be added according to the original structure in order to reduce sounds and vibrations, the structural dynamic modification is implemented. The structural dynamic modification has the object of letting the system have the desired dynamic characteristics after it is modified. If the dynamic properties, which are obtained only from experimental data, can approximate to some degree the modified system properties, then they can be usefully utilized in order to point out locations at which the structure can be efficiently modified.
On this account, recent methods reconstructing the finite element model using the experimental data from real structure have been actively studied. Several review articles of finite element model updating reveal a wealth of updating algorithms but success seems to remain case dependent and applicability is bounded by the skill of the analyst in choosing a correct updating procedure ([1-9]).
This paper suggests structural reanalysis method in which the correlated finite element model is evaluated using FRFs (Frequency Response Functions) of the structure. In this method, the concept of a transformation matrix was introduced and an updated damping matrix of the correlated finite element model was evaluated independently of a mass matrix and a stiffness matrix by means of the FRFs of which noises were filtered out. Updated mass matrix and stiffness matrix of the correlated finite element model could be also evaluated independently of the updated damping matrix. The proposed algorithms adjust the analytical model without iteration. For the purpose of proving effectiveness of the structural reanalysis method proposed in this paper, a numerical test was performed.
2. Structural Reanalysis
The primary objective of the structure experiment performed in the field or laboratory is to understand the actual behavior or innate features of structures under given conditions. The various applications of the test results will also be one of the main objectives. Structural reanalysis is defined as the work that aims to obtain the behaviors of actual structures more precisely by performing various structural analysis based on the analytical model obtained through experiments is usually called the structure reanalysis. In a broader meaning, structure reanalysis is used to precisely obtain the behavior of structures under a different load condition based on the structural behavior observed at one load condition or its own structural feature. As a method of modifying the behavior of structures or the innate structural features to values approximately close to reality by system identification, as well as structure experiment, structure reanalysis is also classified as Structural Dynamic Modification (SDM).
As indicated in Figure 1, the alteration quantity of structure response that corresponds to that of the structure parameter generally tends to be smaller. Thus, to obtain the exact structural parameter of inverse problem that performs the damage detection by applying the system identification, the difference between the analytical response and the observed response should be obviously indicated. On the contrary, identifying the degree of damage through structure reanalysis belongs to the inverse problem in a broader meaning. However, even though some error is included in the correlated analytical model obtained through the system identification, the error in the reanalyzed response is considerably reduced to describe the behavior of the real structure. This relation is described in Equation (1),
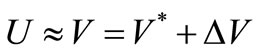 (1)
(1)
where 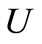 is the actual response of the structure,
is the actual response of the structure,  is the correlated analytical model,
is the correlated analytical model, 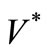 is the initial baseline model, and
is the initial baseline model, and 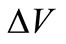 is the response modification value of actual observation. After all, in proportion to the accuracy of response modification value that applies the data actually observed in the structure, the real response of the structure can be predicted more efficiently.
is the response modification value of actual observation. After all, in proportion to the accuracy of response modification value that applies the data actually observed in the structure, the real response of the structure can be predicted more efficiently.
3. Estimation Method for Model Updating
Consider an n-DOF, linear dynamic system of baseline model described by
 (2)
(2)
where 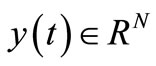 is the vector of generalized coordinates,
is the vector of generalized coordinates,  is the forcing vector,
is the forcing vector,  is the symmetric, positive definite mass matrix,
is the symmetric, positive definite mass matrix,  is the symmetric, positive, semi-definite damping matrix, and,
is the symmetric, positive, semi-definite damping matrix, and, 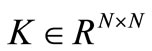 is the symmetric, positive definite stiffness matrix. The over-dot denotes differentiation with respect to time. The frequency response of Equation (2) is given by
is the symmetric, positive definite stiffness matrix. The over-dot denotes differentiation with respect to time. The frequency response of Equation (2) is given by
 (3)
(3)
where 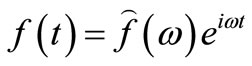 and
and 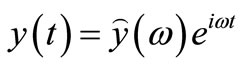 are used. If variable mass, stiffness and damping for model updating are added, Equation (3) can be expressed as
are used. If variable mass, stiffness and damping for model updating are added, Equation (3) can be expressed as
 (4)
(4)
where, 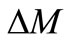 ,
, 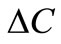 and
and 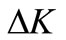 are the n by n variable mass, damping and stiffness matrices for model updating, respectively. Due to physical limitations and time of cost constraints, however, the number of distinct parameters is almost always less than degrees of freedom of the analytical model. Thus, in practice, n < N. By the way,
are the n by n variable mass, damping and stiffness matrices for model updating, respectively. Due to physical limitations and time of cost constraints, however, the number of distinct parameters is almost always less than degrees of freedom of the analytical model. Thus, in practice, n < N. By the way,  ,
,  and
and  depend on the experimental degree of freedom available in the observation experiment of dynamic system, overall system of structure can eventually be condensed in the degree of freedom which is identical to the experimental degree of freedom. Actually, it is impossible to obtain the degree of freedom which is identical to that of the structure. Therefore, only the lower mode response that mainly represents the dynamic system is observed. It is nothing but an approximate solution, because it does not observe all response features of the overall structure system, but merely utilizes the value of the lower mode acquired in the experiment. However, if the value of the lower mode generally represents the structure in the case of civil engineering structures and if the value of the lower mode presents satisfactory measurements, this will not be largely dif-
depend on the experimental degree of freedom available in the observation experiment of dynamic system, overall system of structure can eventually be condensed in the degree of freedom which is identical to the experimental degree of freedom. Actually, it is impossible to obtain the degree of freedom which is identical to that of the structure. Therefore, only the lower mode response that mainly represents the dynamic system is observed. It is nothing but an approximate solution, because it does not observe all response features of the overall structure system, but merely utilizes the value of the lower mode acquired in the experiment. However, if the value of the lower mode generally represents the structure in the case of civil engineering structures and if the value of the lower mode presents satisfactory measurements, this will not be largely dif-
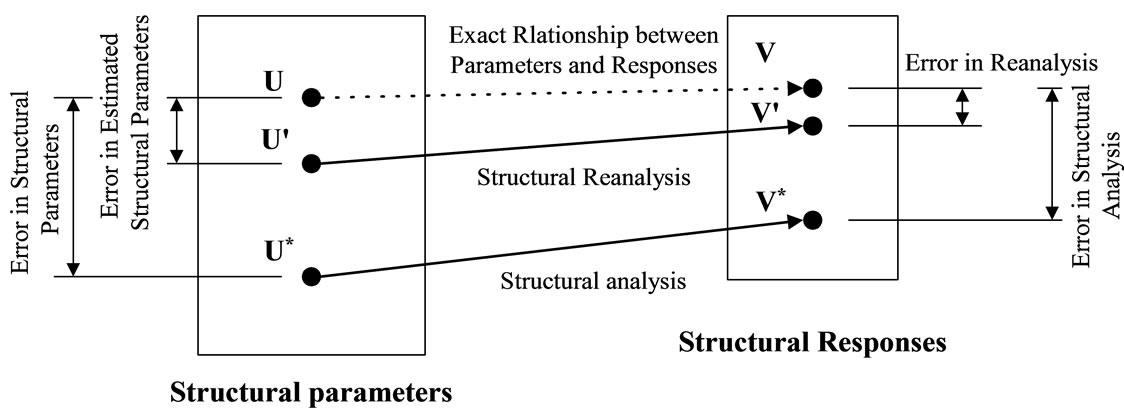
Figure 1. Effects of variation in structural parameters on variation in responses (U and V: exact values, U' and V' : updated values, and U* and V* : initial reference values).
ferent from the accurate values in which more modes are included, but will effectively lessen the degree of freedom of the analytical structure. Thus, the error in calculation can be reduced, with even higher efficiency, thanks to its reduced length. Since the term inside the parentheses represents the inverse of normal FRFs matrix, Equation (4) can be rewritten as
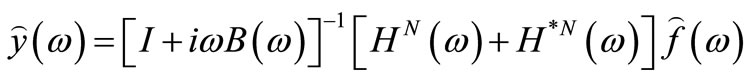 (5)
(5)
where
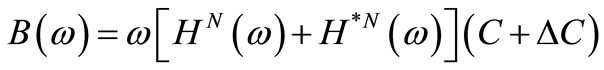 (6)
(6)
is referred to as the transformation matrix. It is noted that 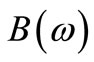 is real matrix. where I is the identity matrix,
is real matrix. where I is the identity matrix,  is the frequency response function matrix of baseline model generated from the normal modes, and
is the frequency response function matrix of baseline model generated from the normal modes, and  is the variable frequency response function matrix for model updating generated from the normal modes. On the other hand, the complex frequency response equation of total dynamic system can also be represented as
is the variable frequency response function matrix for model updating generated from the normal modes. On the other hand, the complex frequency response equation of total dynamic system can also be represented as
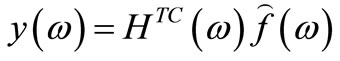 (7)
(7)
where  is the complex frequency response function matrix of total dynamic system. And, it can be actually calculated actuality in the total structure system through an experiment. Note that
is the complex frequency response function matrix of total dynamic system. And, it can be actually calculated actuality in the total structure system through an experiment. Note that 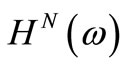 is a square matrix, since it is synthesized from the identified complex modes of total dynamic system by separating
is a square matrix, since it is synthesized from the identified complex modes of total dynamic system by separating 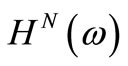 into real and imaginary parts. Comparing Equations (5) and (7), the relationship between the FRFs for complex modes and normal modes is given by
into real and imaginary parts. Comparing Equations (5) and (7), the relationship between the FRFs for complex modes and normal modes is given by
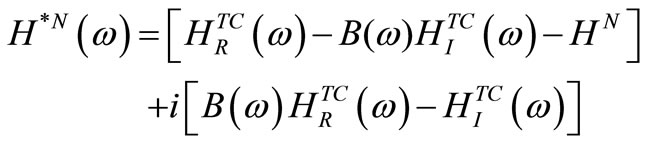 (8)
(8)
where  is the real part of a complex frequency response function matrix of total dynamic system, and
is the real part of a complex frequency response function matrix of total dynamic system, and 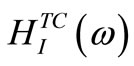 is the imaginary part of a complex frequency response function matrix. Since the left hand side of Equation (8) is a real matrix, so the imaginary part of the right hand side must be equal to a zero matrix for all frequencies and the transformation matrix then
is the imaginary part of a complex frequency response function matrix. Since the left hand side of Equation (8) is a real matrix, so the imaginary part of the right hand side must be equal to a zero matrix for all frequencies and the transformation matrix then 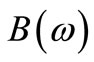 can be solved in terms of the matrices
can be solved in terms of the matrices 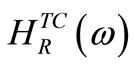 and
and 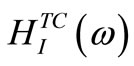 by
by
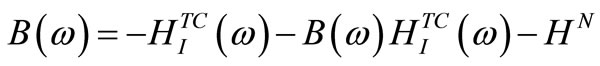 (9)
(9)
Substituting Equation (9) into Equation (8) yields the relation between the normal FRFs matrix and the complex FRFs matrix as
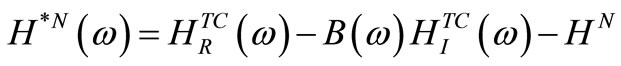 (10)
(10)
From Equations (9) and (10), the transformation matrix 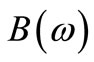 and the variable normal FRFs matrix for model updating
and the variable normal FRFs matrix for model updating  can be calculated, respectively. Once matrices
can be calculated, respectively. Once matrices 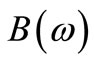 and
and 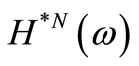 become available, the variable damping matrix for model updating can be calculated from Equation (8). Finally, correlated frequency response function can be expressed by
become available, the variable damping matrix for model updating can be calculated from Equation (8). Finally, correlated frequency response function can be expressed by 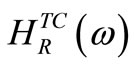 and
and 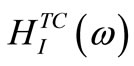 of frequency response function that can get in an experiment of total dynamic system. After all, by applying the FRFs that was obtained in the experiment of all structure system, the correlated analytical model can be reorganized as a modification of the baseline analytical model. This means that the model, unlike the general dynamic analysis, can express the behavior of a real structure more accurately. For a noise-free case, an exact solution for updated damping matrix can be obtained directly from Equation (6) by
of frequency response function that can get in an experiment of total dynamic system. After all, by applying the FRFs that was obtained in the experiment of all structure system, the correlated analytical model can be reorganized as a modification of the baseline analytical model. This means that the model, unlike the general dynamic analysis, can express the behavior of a real structure more accurately. For a noise-free case, an exact solution for updated damping matrix can be obtained directly from Equation (6) by
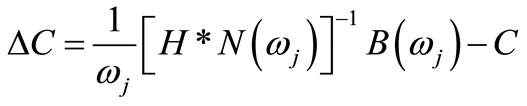 (11)
(11)
where  is chosen frequency. In practice, the frequency response functions are more or less contaminated with noise and the Least Square Method is employed to solve the updated damping matrix. It is noted that the updated damping matrix is identified independently from the mass and stiffness matrices. This is the main difference from the other methods. Next, the identification of updated mass and stiffness matrices is presented. For an undamped system, the equation of motion can be written as
is chosen frequency. In practice, the frequency response functions are more or less contaminated with noise and the Least Square Method is employed to solve the updated damping matrix. It is noted that the updated damping matrix is identified independently from the mass and stiffness matrices. This is the main difference from the other methods. Next, the identification of updated mass and stiffness matrices is presented. For an undamped system, the equation of motion can be written as
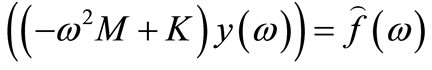 (12)
(12)
The relation between the matrices, 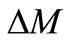 ,
, 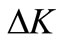 and
and 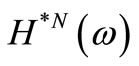 is given by
is given by
 (13)
(13)
where 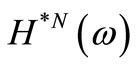 is calculated from Equation (10). Similar to the preceding section, the real overdetermined equation can be obtained and can also be solved by the least squares method.
is calculated from Equation (10). Similar to the preceding section, the real overdetermined equation can be obtained and can also be solved by the least squares method.
4. Numerical Example
Generally speaking, the finite element method is formulated in order to analyze and evaluate the structural systems. But there are some distinct differences between the behavior obtained from a baseline finite element method and that of a real structure [10]. In reality, it is practically impossible to formulate the baseline model considering all errors and then exactly corresponding to the real behavior. Generally the way in which the arbitrary proportional Gaussian noises are added to FRFs is mostly used to mix noises and the experimental data. The most common method for modelling the corruption present on experimental data is to add proportional Gaussian random noise to FRFs where each datum is factored as
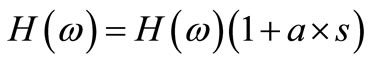 (14)
(14)
where 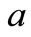 is a normally distributed variable, and s is a user-specified standard deviation. It is unlikely that genuine experimental noise will be either Gaussian of proportional. Arbitrary noises having noise levels of 5% - 10% are employed in the article.
is a normally distributed variable, and s is a user-specified standard deviation. It is unlikely that genuine experimental noise will be either Gaussian of proportional. Arbitrary noises having noise levels of 5% - 10% are employed in the article.
A sample structure employed in the numerical test II as Lembregts [11] suggested has totally 7 degrees of freedom. The shape of the structure is shown in the Figure 2 and the dynamic properties are the same with Equation (15). In the selected sample structure, the third and the fourth modes, and the fifth and sixth modes form very close couples and the damping ratio of the sixth mode, 7% is largest. In conclusion the selected structure is of highly coupled system. In the numerical test, the initially assumed baseline finite element model was assumed to be 90% of true dynamic properties.
 (15)
(15)
As the result of the analysis, it is known that in case of noise-free experimental data the dynamic properties of the estimated correlated finite element model correspond to true values of the structure, and even in case of the noise level of 5% satisfactory results are presented. Figure 3 shows the dynamic parameters of the updated finite
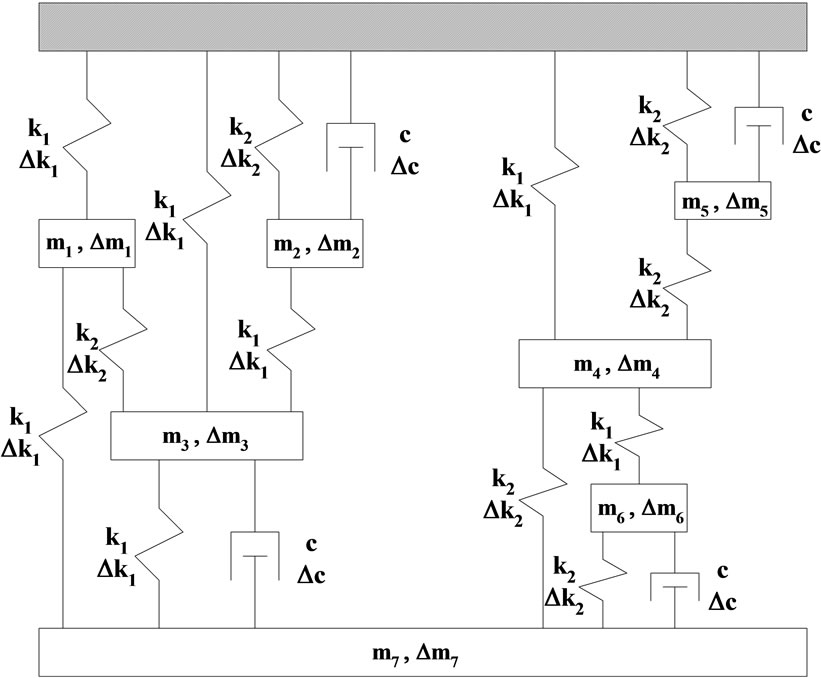
Figure 2. Updated system of 7 degrees of freedom.

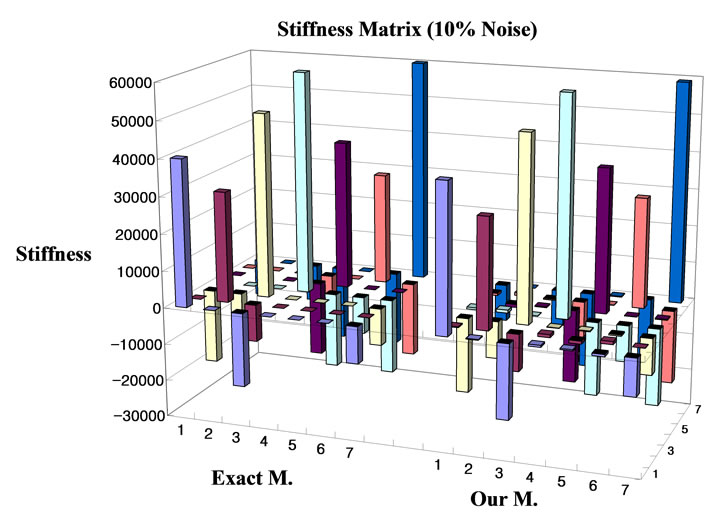
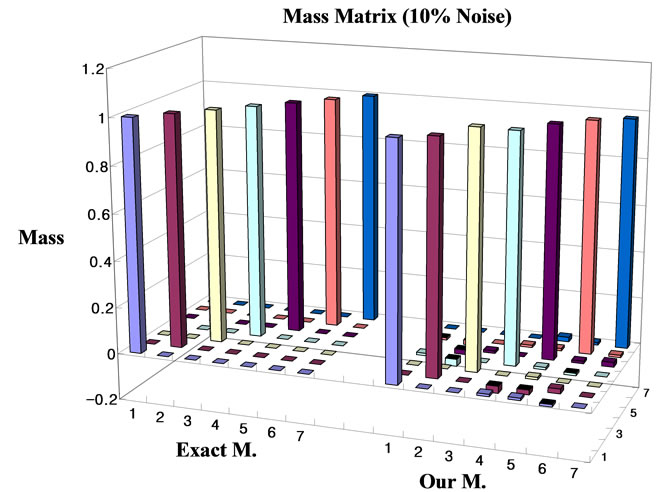
Figure 3. Updated dynamic system matrices (in case of 10% noise level).
element model estimated at the noise level of 10%. The natural frequencies and the damping ratios according to the noise levels (5%, 10%) are indicated in Tables 1-4, where i is th number of modes. The errors are given by
 (16)
(16)
for i = 1, 2, 3, 4, 5, 6, 7, where Error P denotes the relative errors induced by proposed method.
Generally the error which arises in estimating the updated damping matrix is significantly larger than those of the updated mass and the stiffness matrices. It is because the damping effect is much smaller than the mass and stiffness matrices. To overcome this difficulty, the present effort succeeds in updating the damping matrix independently from the updated mass and the stiffness matrices. This is the main difference between the present method and the existing methods. And the method suggested in the article is not to estimate at once the dynamic properties of the structure by using the experimental data in the dynamic system but to present the correlated finite element model by estimating the updated system properties necessary for correcting the initially assumed baseline finite element model. It is known that the method can reduce significantly calculation error, and most importantly error accumulation arising in the calculation because the method estimates the updated damping matrix independently of the mass and the stiffness matrices while existing methods estimate the updated damping matrix while they consider both the mass and the stiffness matrices.
The proposed updating algorithms depend on the connectivities in the baseline finite element model to be correct. Because the basis of model updating is the baseline finite element model, the baseline finite element model must capture certain physical attributes of the actual system. The proposed method, expanding the combination of FRF, can independently estimate the response modification damping from FRF that is observed irrespective of mass matrix or stiffness matrix. Therefore, the accumulation of calculation error can be decreased considerably. The method suggested in this research does not seek, in one time, the dynamic parameters of structure by using data observed in the dynamic system, but suggests

Table 1. Natural frequencies comparisons (5% noise level).

Table 2. Natural frequencies comparisons (10% noise level).

Table 3. Damping ratios comparisons (5% noise level).

Table 4. Damping ratios comparisons (10% noise level).
correlated analytical model by identifying response modification to supplement the initially assumed baseline analytical model. Thus, the error in calculation can be reduced considerably. Furthermore, while the existing methods estimate damping matrix by considering mass and stiffness simultaneously, this method identifies response modification damping irrespective of mass and stiffness matrix. Therefore, the accumulation of error in the calculation is notably reduced.
5. Conclusions
This article suggested the structural reanalysis method evaluating the correlated finite element model corrected by means of the FRFs of the structure. In conclusion, even with noise-mixed data, the suggested method could predict the updated structural system more accurately even with noise-mixed data. The proposed method, expanding the combination of FRF, can independently estimate the response modification damping from FRF that is observed irrespective of mass matrix or stiffness matrix. Therefore, the accumulation of calculation error can be decreased considerably. Also, the results of the article can be properly utilized to evaluate the state of the dynamic system necessary for the maintenance and management of the structure or locate the positions to be modified.
6. REFERENCES
- H. G. Natke, “Updating Computation Models in the Frequency Domain Based on Measured Data: A Survey,” Probabilistic Engineering Mechanics, Vol. 3, 1988, pp. 8-35. doi:10.1016/0266-8920(88)90005-7
- R. M. Lin and D. J. Ewins, “Model Updating Using FRF Data,” Proceedings of ISMA, Vol. 15, 1990, pp. 141-163.
- M. Imregun and W. J. Visser, “A Review of Model Updating Techniques,” Shock and Vibration Digest, Vol. 23, No. 1, 1991, pp. 9-20. doi:10.1177/058310249102300102
- J. E. Mottershead and M. I. Friswell, “Model Updating in Structural Dynamics: A Survey,” Journal of Sound and Vibration, Vol. 167, 1995, pp. 347-375. doi:10.1006/jsvi.1993.1340
- A. Bhasiar, S. S. Sahu and B. C. Nakra, “Approximations and Reanalysis over Parameter Interval for Dynamic Design,” Journal of Sound and Vibration, Vol. 248, No. 1, 2001, pp. 178-186. doi:10.1006/jsvi.2001.3686
- C. Mares, J. E. Mottershead and M. I. Friswell, “Stochastic Model Updating: Part 1—Theory and Simulated Example,” Mechanical Systems and Signal Processing, Vol. 20, No. 7, 2006, pp. 1674-1695. doi:10.1016/j.ymssp.2005.06.006
- C. Joao, N. D. Biswa, G. Abhijit and L. Maitreya, “A Direct Method for Model Updating with Incomplete Measured Data and without Spurious Modes,” Mechanical Systems and Signal Processing, Vol. 21, No. 7, 2007, pp. 2715-2731. doi:10.1016/j.ymssp.2007.03.001
- E. Capiez-Lernout and C. Soize, “Robust Updating of Uncertain Damping Models in Structural Dynamics for Lowand Medium-Frequency Ranges,” Mechanical Systems and Signal Processing, Vol. 22, No. 8, 2008, pp. 1774-1792. doi:10.1016/j.ymssp.2008.02.005
- V. Arora, S. P. Singh and T. K. Kundra, “Further Experience with Model Updating Incorporating Damping Matrices,” Mechanical Systems and Signal Processing, Vol. 24, No. 5, 2010, pp. 1383-1390. doi:10.1016/j.ymssp.2009.12.010
- S. R. Ibrahim and A. Sestieri, “Analysis of Errors and Approximations in the Use of Modal Coordinates,” Journal of Sound and Vibration, Vol. 177, No. 2, 1994, pp. 145-157. doi:10.1006/jsvi.1994.1424
- F. Lembregts and M. Brughmans, “Estimation of Real Modes from FRFs via Direct Parameter Identification,” Proceedings of 7th International Modal Analysis Conference, Las Vegas, 30 January 1989, pp. 631-636.

