Engineering
Vol. 2 No. 12 (2010) , Article ID: 3605 , 4 pages DOI:10.4236/eng.2010.212120
Parameters Optimization of Multi-Branch Horizontal Well Basing on Streamline Simulation
Key Laboratory of Ministry of China on Enhanced Oil and Gas Recovery, Northeast Petroleum University,
Daqing, China
E-mail: chenxirui334@163.com
Received October 26, 2010; revised November 1, 2010; accepted November 8, 2010
Keywords: Streamline Simulation, Multi-Branch Horizontal Well, Optimization, Waterflood, Sweep Efficiency
ABSTRACT
As a highly efficient production method, the technique of multi-branch horizontal well is widely used in low permeability reservoirs, heavy oil reservoirs, shallow layer reservoirs and multi-layer reservoirs, because it can significantly improve the productivity of a single well, inhibit coning and enhance oil recovery. Study on sweep efficiency and parameters optimization of multi-branch horizontal well is at the leading edge of research. Therefore, the study is important for enhancing oil recovery and integral exploitation benefit of oil fields. In many applications, streamline simulation shows particular advantages over finite-difference simulation. With the advantages of streamline simulation such as its ability to display paths of fluid flow and acceleration factor in simulation, the flooding process is more visual. The communication between wells and flooding area has been represented appropriately. This method has been applied to the XS9 reservoir in Daqing Oilfield. The production history of this reservoir is about 10 years. The reservoir is maintained above bubble point so that the simulation meets the slight compressibility assumption. New horizontal wells are drilled following this rule.
1. Introduction
Using multi-branch horizontal wells to enhance oil recovery has been applied widely all over the world and it is necessary for low permeability reservoirs’ development. In the long process of practice, it was discovered that the advantages of multi-branch horizontal well were not made full use of but only the drilling techniques not the combination with the actual development conditions were paid attention to. The relationship among length of branch, angle of branch and distance of branches produces great effect on sweep efficiency. So the parameters of multi-branch horizontal well require optimizing.
As the application of high-resolution geologic models in simulations, more attention had been paid to the use of simulation in oil field development. Finite difference method which applied widely cannot meet the needs such as high computational efficiency and being visually appealing. So the 3D streamline simulation approach has been applied to simulation as complementary to finite difference simulation techniques [1-4].
Streamline simulation is in the advanced and matured stage in slightly compressible system. It calculates the saturation via 1D streamline instead of saturation field [5-7]. Both computational efficiency and matching high resolution geologic models become possible. Unlike the unity of the saturation in finite difference grid cell, streamline simulation provides several values of the saturation in one grid cell, and then the fineness of the solution gets elevated [8,9].
Taking advantage of streamline simulation’s particular capability, the relationship among length of branch, angle of branch and distance between branches has been optimized by orthogonal experiment method.
2. Streamline Simulation Theory
2.1. Velocity Field Solution and Streamline Tracing
The streamline model is a model with the assumptions as follows: 1) Considering the effects of gravity and capillary; 2) There are oil phase and water phase in the reservoir; 3) The fluid flow in the reservoir is incompressible; 4) The fluid flow obeys Darcy’s Law; 5) The flow is under an isothermal condition. On the basis of these assumptions, and utilizing the continuity equation and flow equation, the pressure equation of streamline model can be established as follows:
 (1)
(1)
Where λo, λw are, respectively, mobility of oil and water, μm2/Pa·s; λt is total mobility, μm2/Pa·s; γo, γw are, respectively, gravities of oil and water, dimensionless; qvo, qvw are volume flow rate of producer and injector, m3/s; qv is the total flow rate of injection or production wells, m3/s; D is the depth from the reference level, its direction is the same to gravity acceleration, m; pcow is the capillary force between oil phase and water phase, Pa.
Equation (1) can be solved by finite difference method. And the pressure distribution, i.e., pressure field, can be derived.
According to the pressure field, streamline tracing is implemented by using Pollock method which is defined with the following assumptions: the velocity field in a grid cell as a linear interpolation, and the velocity in each direction is only a function of the coordinate in that direction.
In a 2D grid system, with the pressure at the face, the potential at the face of the grid cell can be calculated. Then the velocity in each direction is derived, the TOF can be calculated also. The face at which the streamline exits is the one corresponding to the minimum positive exit time. The exit point will be the entry point of the adjacent grid cell, repeating this calculation process until the result converges to the grid cell which a production well is in. Connecting the exit points in chronological, an integrated streamline can be derived.
In a 3D system, the exit points can be obtained by utilizing Pollock method to calculate the values in the z-direction. By connecting these points, production and injection wells, the streamline can be derived.
The advantages of this method: being analytical; and it constructs a velocity field that satisfies the flux conservation condition.
2.2. Saturation Field
After the pressure filed is solved and the streamlines are traced by utilizing finite difference method, the next step is to solve the saturation along the streamlines by introducing the time-of-flight concept. The time-of-flight is defined as the time required for a particle to travel a distance along the streamline,
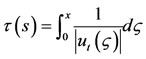 (2)
(2)
In streamline tracing, the time for streamlines across each grid cell, Δte,i , can be calculated using Pollock method. The time of flight can be expressed as follow:
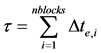 (3)
(3)
Where nblocks designates the number of grid cells when a particle travel a distance as s; Δte,i is the time for a particle to travel through the i’th cell.
A. Distribution of volumetric flux of streamline. Tracing streamline from the cell of injection well to the cell of production well. For a grid cell with source or sink, as the streamline is not linear in segments, the streamline generalizes from the face of the grid cell instead of generalizing from the centre of the grid cell.
For simplicity, distribution of flux is based on changing the number of streamlines with different flow rate of injection well, and the volumetric flux along each streamline is constant. The higher injection flow rate, the more streamlines. Similarly, much more streamlines can be traced in a high flow rate region.
In grid cell (i,j,k) with a source, the volumetric flux at the interface (i±1/2,j,k) of grid cell (i,j,k) and grid cell (i±1,j,k) is Qi±1/2,j,k. The volumetric flux along each streamline is qsli±1/2,j,k at the interface (i±1/2,j,k). The number of streamlines generalized from this face is ni±1/2,j,k can be expressed as follow:
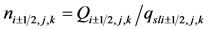 (4)
(4)
where Qi±1/2,j,k is given as:
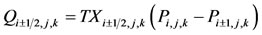 (5)
(5)
where TXi±1/2,j,k represents the transmissibility in the x-direction of oil phase and water phase between the grid cell (i±1,j,k) and the grid cell (i,j,k); Pi,j,k is the pressure in the grid cell (i,j,k).
Similarly, the number of streamlines on other faces can be obtained.
B. Establishing the saturation equation in streamline model. Considering capillary effect, the fluid flow equation can be expressed as follow:
 (6)
(6)
Combining with saturation equation and mass conservation equation, the saturation equation of streamline model for oil-water two phases can be derived:
 (7)
(7)
Simplified as:
 (8)
(8)
where  is defined as:
is defined as:
 (9)
(9)
C. Numerical solution for saturation equation of streamline model. Because the derived equation is a complicated convective diffusion equation, for simplicity, solve the convection term, gravity and capillary item in a saturation equation by utilizing the technique of operator separation. The convective diffusion equation can be divided to two parts, one is a nonlinear hyperbolic equation describing the convection term, the other one is a parabolic equation describing the effects of gravity and capillary.
As the streamlines generate from the grid cell face of injection well and dissolved at the grid cell face of the production well, the field along streamlines is sourcefree.
Decoupling Equation (8) by utilizing operator separation technique, two equations are obtained as follows:
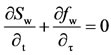 (10)
(10)
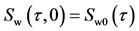
 (11)
(11)
Equation (10) is a 1D saturation equation, and can be solved by 1D numerical solution along streamlines (transformation of the 3D equation to 1D equation). The solution for (10) is assumed as Sf(t). Equation (11) is a saturation equation considering the effects of gravity and capillary, and can be solved only by 3D numerical solution. The solution for Equation (11) is assumed as H(t). Finally, the solution at time tn(tn =nΔt) is derived as:
 (12)
(12)
2.3. Streamline Update
For the actual development process in the oil field, well pattern and production system is not fixed. Especially for the oil filed with very long production periods, we often need to establish some methods to stimulate, such as pattern adjustment, shut-in, isolation of individual zones and water shut off, fracturing and acidizing, infilling, which will change the streamline distribution. So we have to update the streamlines immediately after those conditions to accurately represent the displacing dynamic information.
2.4. Compare with Finite Difference Simulation
Comparing the water cut of streamline simulation and finite difference simulation, it is easy to know that the streamline simulation’s result is more close to the historical data at initial stage. This is because the improvement on saturation calculation. So streamline simulation is more suitable for study on flooding.
3. Optimization of Branch Parameters
3.1. Simulation of Multi-Branch Horizontal Wells
The flow field of flooding unit in combined well pattern of horizontal and vertical wells is drawn based on the result of simulations as Figure 1. As shown in Figure 1, the streamline model presents flow field more intuitive. Because the streamline simulation calculates the saturation via 1D streamline, it gets higher resolution than finite difference simulation in low water cut stage. Streamline simulation is more suitable for study on flooding.
3.2. Orthogonal Experimental Design
In flooding unit containing multi-branch horizontal well, the main factors affecting the sweep efficiency are length of branch, angle of branch and distance between
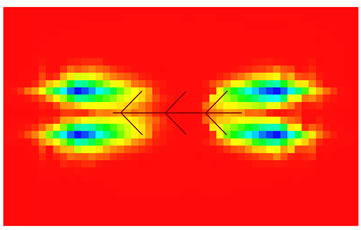 (a)
(a)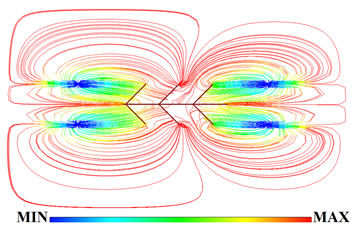 (b)
(b)
Figure 1. Streamlines representing oil saturation.
branches. In orthogonal design experiments, influence factors are called factors, and the data points of factors are called levels. As shown in Table 1, there are three factors which effect development, so using L9 (33)-type orthogonal to arrange experiments.
Basing on the orthogonal experimental design table, orthogonal experiment is designed as Table 2.
3.3. Simulation of Orthogonal Experiment
Simulation is run and the sweep efficiency is recorded when water cut is 98%. The results of streamline simulation show that NO. 6 project has the highest sweep efficiency with the number 68.9%. As shown in Table 3, the results of simulation cannot distinguish the sequence of priority of factors. To study the impact on sweep efficiency by factors the range of factors should be analyzed.
3.4. Analysis of Factors
According to the size of range, the impact of factor on the size of the experimental results can be determined. In orthogonal experiment method, range is the difference between the maximum and minimum values at different levels of the same factor. The bigger range a factor hasthe more it influences the size of the experimental result.
Before the analysis of the sequence of priority of factors, the experimental result should be processed as follows: 1) Sum the values of results in same level of one factor. As there are three levels in one factor, K1, K2 and K3 are used to indicate the sums respectively. 2) Average the values of results in same level of one factor. Use
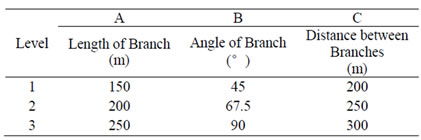
Table 1. Factors and levels.
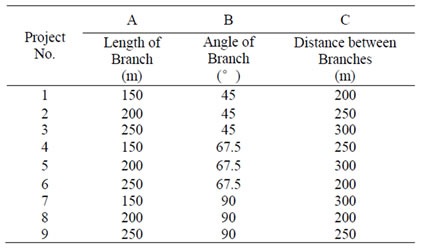
Table 2. Orthogonal Experiment.
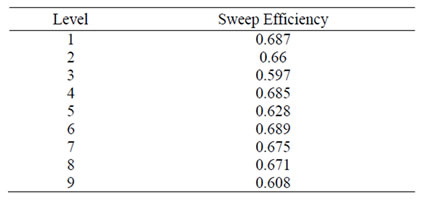
Table 3. Results of simulation.
k1, k2 and k3 to indicate the averages respectively. 3) Solve the size of range of each factor, and use R to indicate it.
According to the above rules, the ranges are calculated in Table 4. It shows that the range of factor A is the biggest with the value 0.066. In consequence, the main factor is the length of branch, followed by distance between branches and then the angle of branch. The sequence of priority of factors is as follow: A>C>B.
4. Conclusions
In this paper, the streamline model considering multi-branch horizontal well is derived. The streamlines provide us with a clear picture of flow field of flooding unit in combined well pattern of horizontal and vertical wells.
The simulation results indicate that streamline simulation gets higher resolution than finite difference simulation in low water cut stage.
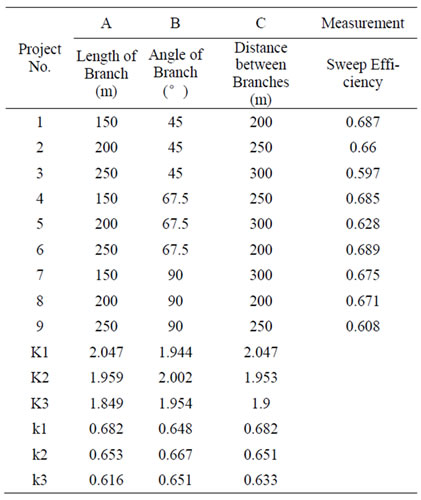
Table 4. The range of experimental result The leading influencing factor on sweep efficiency is length of branch.
5. Acknowledgments
This author gratefully acknowledges financial support from Heilongjiang Provincial Science and Technology Plan Project (Grant No: GZ09A407) and National Science Foundation of China (Grant No: 50874023) and Research Program of Innovation Team of Science and Technology in Enhanced Oil and Gas Recovery (Grant No: 2009td08).
6. REFERENCES
- G. H. Grinestaff and D. J. Caffrey, “Waterflood Management: A Case Study of the Northwest Fault Block Area of Prudhoe Bay, Alaska, Using Streamline Simulation and Traditional Waterflood Analysis,” Society of Petroleum Engineers Annual Technical Conference and Exhibition, Dallas, 1-4 October 2000, pp. 63152-MS.
- A. Chakravarty, D. B. Liu and S. Meddaugh, “Application of 3D Streamline Methodology in the Saladin Reservoir and Other Studies,” Society of Petroleum Engineers Annual Technical Conference and Exhibition, Dallas, 1-4 October 2000, pp. 63154-MS.
- T. Lolomari, K. Bratvedt, M. Crane, W. J. Milliken and J. J. Tyrie, “The Use of Streamline Simulation in Reservoir Management: Methodology and Case Studies,” Society of Petroleum Engineers Annual Technical Conference and Exhibition, Dallas, 1-4 October 2000, pp. 63157-MS.
- G. H. Grinestaff, “Waterflood Pattern Allocations: Quantifying the Injector to Producer Relationship with Streamline Simulation,” Society of Petroleum Engineers Annual Technical Conference and Exhibition, Dallas, 1-4 October 2000, pp. 54616-MS.
- M. R. Thiele, “Streamline Simulation,” The 6th International Forum on Reservoir Simulation, Schloss Fuschl, 3-7 September, 2001.
- M. R. Thiele and R. P. Batycky, “Using Streamline-Derived Injection Efficiencies for Improved Waterflood Management,” Society of Petroleum Engineers Reservoir Evaluation & Engineering, Vol. 9, No. 2, 2006, pp. 187-196.
- R. P. Batycky, A. C. Seto and D. H. Fenwick, “Assisted History Matching of A 1.4-Million-Cell Simulation Model for Judy Creek ‘A’ Pool Waterflood/HCMF Using a Streamline-Based Workflow,” Society of Petroleum Engineers Annual Technical Conference and Exhibition, Anaheim, 11-14 November 2007, pp. 108701-MS.
- A. Datta-Gupta and M. J. King, “Streamline Simulation: Theory and Practice,” Society of Petroleum Engineers Textbook Series, Richardson, Vol. 11, 2007, p. 404.
- R. P. Batycky, M. R. Thiele, R. O. Baker and S. H. Chugh, “Revisiting Reservoir Flood-Surveillance Methods Using Streamlines,” Society of Petroleum Engineers Reservoir Evaluation & Engineering, Vol. 11, No. 2, 2008, pp. 387-394.

