ABSTRACT

We propose a global warfare model that integrates the models of the whole tensor-centric warfare series, represented as a high-dimensional entangled warfare category. Its underpinning metaphysics is “entangled fusion”: this is the macroscopic entanglement concept inspired by high-dimensional (HD) quantum computation (the “quantum brain”), in which any number of entangled wave-functions can be highly correlated, with neuron-like signaling among them. From this entangled perspective, war and battle is seen essentially as a holistic phenomenon: if any one of a set of mutually entangled warring parties is removed from the equation, then the war as it is instantly stops, possibly to be replaced by a new conflict between the remaining parties but distinct from that which it supplants. The formal global warfare framework developed in this paper expresses this fundamental idea of arbitrary many interrelated/entangled conflicts, each of them defined by its own battle-manifold (with warfighting tensor fields acting on it) and occurring (more-or-less) simultaneously on the planet; we call this entangled category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$.

Keywords:

Tensor-Centric Warfare, Global Warfare Model, Entangled Warfare Category

1. Introduction

As a natural integration of the tensor-centric warfare series (TCW, see [1] [2] [3] [4] [5] ), in this paper we propose a global warfare model.

The basic concept of Global Warfare introduced in this paper concerns an attempt to realize a holistic approach to modeling war and battle. Until recently, the vast majority of works in this topic have focused on representing dynamics of individual battles or missions. Yet, this approach fails to address the complexity of modern warfare, and particularly the nonlinear and non-local nature of interactions and consequences, thus compelling us to examining wars not just as series of battles, and battles as not just as series of missions, in temporal sequence. Rather, we seek here to model war as arbitrary collections of overlapping battles and battles as collections of missions, which can unfold simultaneously and can interact with one another.

This increasing complexity and interdependence means that to better design appropriate future force capability and operating methods, strategies and tactics, a more holistic approach to modeling is required. As a consequence of this need for more holistic methods, we need to be able to capture all the interdependencies between various overlapping battles and simultaneous operations in different theaters, and among events during any given war, battle or mission. The intent in this paper is to create a formal mathematical framework through the utility of Tensors and the concept of entanglement to capture this global view of war and battle, which constitutes then a national or multi-national perspective.

It has been long recognized that warfare is a highly complex phenomenon that contains both elements of order and of chaos, usually with both co-occurring. It can be said that, all other things being equal, the victor will be the side that makes the least errors; or, to put it another way, the side that is able to cope with the chaos the most effectively. We recognize that complex systems lead to emergent patterns and behaviors which can only be understood through modeling and simulations if the model or simulation has captured adequately the large-scale interrelationships that connect all the activities and events that collectively comprise a global picture of war and battle from a national perspective.

The central idea of the present paper, the underlying thought-current reflecting our holistic view of warfare, is the concept of a large-scale warfighting fusion, or complex, consisting of many interrelated battlefields, that is, an entangled fusion¹ of warfighting. In other words, we see a modern warfare as a compound whole, an inseparable fusion, almost having a mind-like character, comprising a number of non-local yet interacting battlefields-rather than a reducible, disjoint sum of passive mechanistic components.

The entangled fusion is a macroscopic concept inspired by high-dimensional (HD) quantum computation, called the “quantum brain”, in which any number of entangled wave-functions can be highly-correlated, inseparable and with neuron-like signaling among them. The entanglement is visible in any macroscopic system or process which cannot be completely reduced to its components, but that manifests behavior only as a whole compound/fused system. Biological systems like various swarming behaviors of bees, birds and bats show this characteristic. By analogy, in this paper we claim that the concept of a global warfare is essentially an entangled fusion of two (or possibly more) parties at least some of whom are in a state of conflict; the war cannot exist without conflicting parties though not all parties need to simultaneously be in conflict at any one time. Any attempt to reduce such a phenomenon into independent passive components is necessarily limited at best and generally unrealistic and hence misleading. Furthermore, if any one of mutually entangled parties is removed from the equation then the state of warfare as it has existed until that point instantly stops, possibly to be replaced with another. In other words, war is essentially a holistic phenomenon, both in terms of human populations involved and in terms of (futuristic) autonomous cyber-physical-cognitive systems (CPC-systems, introduced in [6] ).

Seen in this way, major historical conflicts such as World War I and II comprise not distinct events but more like pronounced clusters of overlapping component conflicts that evolved over time, as parties shifted alliances and entered and exited different levels of states of hostility and cooperation with each other. The change in stance in World War 2 of the USA from supporting Britain with materiel to entering fully into the conflict, the Japanese attack on Pearl Harbor, the breakdown of the German-Soviet non-aggression pact with Germany’s attack on the Soviet Union, the Winter War between Russia and the USSR, and the capitulation of Italy all represent shifting elements of the overall conflict with changing allegiances and levels of conflict. Furthermore, the Second World War did not occur in isolation of other conflicts, but rather was preceded and influenced by a host of disparate conflicts, including the Spanish Civil War, Italy’s invasion of Ethiopia, the Japanese invasion of China, and the ongoing sociopolitical consequences of the First World War, and was then immediately supplanted by the Cold War.

A formal framework developed in this paper to represent national and international viewpoint of war and battles and to express this fundamental observation that conflicts are not isolated but, at least from a national perspective, comprise many interrelated/entangled conflicts at various degrees of involvement, occurring (more-or-less) simultaneously on the planet, is called the entangled warfare category.

2. Entangled Tensor Categories

The basic algebraic operator which we use to represent entangled fusion is the ordinary tensor product and its categorical abstraction. Specifically, the Kronecker tensor product, usually denoted by “ $\otimes$ ” and based on the Cartesian product², is ubiquitous in mathematical sciences. For example, we have used it in Riemannian and Kähler geometries in [4] to define their respective metrics (using summation convention) written by:

$g_{Riem}=g_{ik}d{x}^i\otimes d{x}^k\text{and}{g}_{K\ddot{a}hler}=g_{i\overline{k}}d{z}^i\otimes d{z}^{\overline{k}}\mathrm{,}$

as the tensor products $\otimes \mathrm{<mo>\; :\; </mo>}{M}_{Riem}\times M_{Riem}\to M_{Riem}$ of the differentials of local real coordinates $\left\{x^i,i=1,\cdots ,n\right\}$ in the Riemannian case, and $\otimes \mathrm{<mo>\; :\; </mo>}{M}_{K\ddot{a}hler}\times M_{K\ddot{a}hler}\to M_{K\ddot{a}hler}$ of the differentials of local holomorphic coordinates $\left\{z^i\mathrm{,}{z}^{\overline{i}}\right\}$ in the Kähler case. In both cases, $M\times M$ represents the Cartesian product of the manifold M with itself.

In the same way, both linear and quadratic Lanchester-type TCW-terms (see [1] ):

$\text{Red:}\stackrel{Red\mathrm{.}vecfield}{\overbrace{{\partial }_t{R}^a}}=\stackrel{lin\mathrm{.}Lanchaster}{\overbrace{k{A}_b^a{B}^b}}+\stackrel{quad\mathrm{.}Lanchaster}{\overbrace{k_b{F}_{cd}^{ab}{R}^c{B}^d}}\in M_{\text{Red}}\mathrm{,}$

$\text{Blue:}\stackrel{Blue\mathrm{.}vecfield}{\overbrace{{\partial }_t{B}^a}}=\stackrel{lin\mathrm{.}Lanchaster}{\overbrace{\kappa C_b^a{R}^b}}+\stackrel{quad\mathrm{.}Lanchaster}{\overbrace{{\kappa }_b{G}_{cd}^{ab}{R}^c{B}^d}}\in M_{\text{Blue}}\mathrm{,}$

implicitly use tensor products between all included tensor fields (of 0th, 1st, 2nd and 4th order). Explicitly, these TCW-equations read:

$\text{Red:}\stackrel{Red\mathrm{.}vecfield}{\overbrace{{\partial }_t{R}^a}}=\stackrel{lin\mathrm{.}Lanchaster}{\overbrace{k\otimes A_b^a\otimes B^b}}\mathrm{<mi>\; </mi>}+\stackrel{quad\mathrm{.}Lanchaster}{\overbrace{k_b\otimes F_{cd}^{ab}\otimes R^c\otimes B^d}}\in M_{\text{Red}}\mathrm{,}$

$\text{Blue:}\stackrel{Blue\mathrm{.}vecfield}{\overbrace{{\partial }_t{B}^a}}=\stackrel{lin\mathrm{.}Lanchaster}{\overbrace{\kappa \otimes C_b^a\otimes R^b}}+\stackrel{quad\mathrm{.}Lanchaster}{\overbrace{{\kappa }_b\otimes G_{cd}^{ab}\otimes R^c\otimes B^d}}\in M_{\text{Blue}}\mathrm{.}$

In addition, the Red + Blue battle Hamiltonian, $H=-J_{ab}{R}^a{B}^b$, with its Ising-type connection tensor, $J_{ab}=A_b^a{C}_a^b{\eta }_{ab}$ (proposed in [3] ), is explicitly written as: $H=-J_{ab}\otimes R^a\otimes B^b$, with $J_{ab}=A_b^a\otimes C_a^b\otimes {\eta }_{ab}$.In all these TCW examples, the tensor product $\otimes$ is used as a “glue” to stick together various tensor fields into coherent/inseparable terms, representing coherent/inseparable warfighting actions.

Similarly, in quantum computation, a compound system ${|\psi \rangle }_1\otimes {|\psi \rangle }_2$ consists of two entangled wave-functions, ${|\psi \rangle }_1$ and ${|\psi \rangle }_2$, which can be physically far-apart but still have their maximally-entangled Bell-states³: ${|\psi \rangle }_{12}={|\psi \rangle }_1\otimes {|\psi \rangle }_2$ -lives in the tensor product ${\mathcal{H}}_1\otimes {\mathcal{H}}_2$ of their respective Hilbert spaces of states, ${\mathcal{H}}_1$ and ${\mathcal{H}}_2$ ⁴. Therefore, in quantum computation, the tensor product $\otimes$ acts both locally, on the wave-functions, as $\otimes \mathrm{<mo>\; :\; </mo>}{|\psi \rangle }_1\times {|\psi \rangle }_2\to {|\psi \rangle }_1\otimes {|\psi \rangle }_2$ (where ${|\psi \rangle }_1\times {|\psi \rangle }_2$ is the Cartesian product of the wave-functions), and globally, on their respective Hilbert spaces, as $\otimes \mathrm{<mo>\; :\; </mo>}{\mathcal{H}}_1\times {\mathcal{H}}_2\to {\mathcal{H}}_1\otimes {\mathcal{H}}_2$ (where ${\mathcal{H}}_1\times {\mathcal{H}}_2$ is the Cartesian product of the Hilbert spaces). Generalization to any number of wave-functions (and their respective Hilbert spaces of states) is straightforward.

Now, inspired by quantum computation, suppose that we have a pair of generic CPC-systems: A (called Alice) and B (called Bob)⁵, and we want to fuse them into one system, a single entangled $\left[\text{Alice}\otimes \text{Bob}\right]$ -compound, denoted by $A\otimes B$.The most natural framework for such a combination is a tensor category, a rigorous-yet-flexible functional architecture, defined as follows. Firstly, recall (from Appendix 6) that classical category theory includes objects (CPC-systems: $A\mathrm{,}B\mathrm{,}C\mathrm{,}\cdots$ ) and morphisms (processes of any nature between the CPC-systems: $A\stackrel{f}{\to }B\mathrm{,}B\stackrel{g}{\to }C\mathrm{,}\cdots$ ). This two-fold collection of objects/systems and morphisms/processes between them is governed by the functional composition, denoted by “ $\circ$ ”, a temporal/sequential composition in which the output of the first process $f\mathrm{<mo>\; :\; </mo>}A\to B$ becomes the input to the second process $g\mathrm{<mo>\; :\; </mo>}B\to C$ etc., formally defined as: $A\stackrel{f}{\to }B\stackrel{g}{\to }C=Ag\circ fC$.The extension to a chain of many sequential processes is straightforward.

Secondly, to be able to include compound/fused CPC-systems of arbitrary nature, where two subsystems act as an entangled/coherent whole, we need to extend the standard definition of a category, which is based on the serial/temporal composition “ $\circ$ ”, with a new notion of parallel/spatial composition (i.e., entangled fusion)⁶. Such an enriching of a standard category theory can be done using the special functor $\otimes$, called the symmetric monoidal tensor product⁷ (or, tensoring functor $\otimes$, for short)―a categorical generalization of the Kronecker tensor product (used above to glue together tensorial expressions), which acts both on objects and on morphisms of a category, along with its compound operations: $A\otimes Bf\otimes gC\otimes D$, inherited from the operations on the individual subsystems.

Briefly, we define a symmetric monoidal tensor (SMT) category $\mathcal{C}$ ⁸, using the tensoring functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ that acts on a pair $\left(\text{Ob}\left(\mathcal{C}\right)\mathrm{,}\text{Mor}\left(\mathcal{C}\right)\right)$ of generic objects of $\mathcal{C}$ : $A\mathrm{,}B\mathrm{,}\cdots \in \text{Ob}\left(\mathcal{C}\right)$ and generic morphisms (arrows) between objects of $\mathcal{C}$ : $f\mathrm{<mo>\; :\; </mo>}A\to B\mathrm{,}g\mathrm{<mo>\; :\; </mo>}B\to C\mathrm{,}\cdots \in \text{Mor}\left(\mathcal{C}\right)$, where $\mathcal{C}\times \mathcal{C}$ represents the Cartesian product of the category $\mathcal{C}$ with itself. The action of the tensoring functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ is given on objects and morphisms of $\mathcal{C}$ by:

$\text{Ob}\left(\mathcal{C}\right)\mathrm{<mo>\; :\; </mo>}\left\{A\mathrm{,}B\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}A\otimes B\equiv B\otimes A\mathrm{,}$

$\text{Mor}\left(\mathcal{C}\right)\mathrm{<mo>\; :\; </mo>}\left\{A\stackrel{f}{\to }B\mathrm{,}C\stackrel{g}{\to }D\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}A\otimes Cf\otimes gB\otimes D\mathrm{.}$

The main characteristic of the tensoring functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ is the so-called commutative bifunctoriality⁹: the order in which two operations, f (applied to one subsystem) and g (applied to another subsystem), does not matter (for the proof of the commutative bifunctoriality see [12] as well as [13] , [14] ). Briefly, for any quadruple ( $A_1\mathrm{,}{A}_2\mathrm{,}{B}_1\mathrm{,}{B}_2$ ) of CPC-systems with the corresponding quadruple of processes ( $f_1\mathrm{,}{f}_2\mathrm{,}{g}_1\mathrm{,}{g}_2$ ) between them, we have the following bi-compositional rule:

$\left(g_1\otimes g_2\right)\circ \left(f_1\otimes f_2\right)=\left(g_1\circ f_1\right)\otimes \left(g_2\circ f_2\right)\mathrm{.}$

This rule is the “signature” of any SMT category $\mathcal{C}$.It states that any combinations of serial and parallel compositions of CPC-systems are commutative―their order doesn’t matter, due to the symmetry of the tensoring functor $\otimes$(in spite of the time-asymmetry of the serial composition“ $\circ$”).

In this way defined SMT category $\mathcal{C}$ represents a collection of objects/systems and morphisms/processes, combined in two ways: using both sequential composing and parallel tensoring operations-in order to formulate a rigorous compositional theory (see [15] ). This powerful architecture is capable of assembling large and open¹⁰ input-output CPC-systems, by composing and tensoring of many component transfer functions (examples include linear/nonlinear control systems, electric/mechatronics circuits, signal/bond flow graphs, chemical/social networks and deterministic/stochastic Petri nets).

In the next section, we will use a large-scale SMT category $\mathcal{C}$, called the warfare category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$, which is inspired by HD quantum-computation in order to represent a global warfare model. To start the quantum-computation formalism with a simple 2D example, we say that two Hilbert spaces, ${\mathcal{H}}_A$ and ${\mathcal{H}}_B$, are objects of the SMT category $ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2$ with the quantum tensoring functor, $\otimes \mathrm{<mo>\; :\; </mo>}ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2\times ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2\to ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2$, given by:

$\text{Ob}\left(ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2\right)\mathrm{<mo>\; :\; </mo>}\left\{{\mathcal{H}}_A\mathrm{,}{\mathcal{H}}_B\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}{\mathcal{H}}_A\otimes {\mathcal{H}}_B\equiv {\mathcal{H}}_B\otimes {\mathcal{H}}_A\mathrm{,}$

$\text{Mor}\left(ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2\right)\mathrm{<mo>\; :\; </mo>}\left\{{\mathcal{H}}_A\stackrel{f}{\to }{\mathcal{H}}_B\mathrm{,}{\mathcal{H}}_C\stackrel{g}{\to }{\mathcal{H}}_D\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}{\mathcal{H}}_A\otimes {\mathcal{H}}_{C}f\otimes g{\mathcal{H}}_B\otimes {\mathcal{H}}_D\mathrm{,}$

where the tensor product of Hilbert spaces:

${\mathcal{H}}_A\otimes {\mathcal{H}}_B=\left\{{\displaystyle \sum _{k\mathrm{,}j}}{\omega }_{kj}\cdot {|k\rangle }_A\otimes {|j\rangle }_B\mathrm{,}\text{weighted}\text{by}\left({\omega }_{kj}\in ℂ\text{for}\text{all}k\mathrm{,}j\right)\right\}$

includes the entangled $\left[\text{Alice}\otimes \text{Bob}\right]$ Bell-state¹¹:

${|\psi \rangle }_{AB}\equiv {|\psi \rangle }_A\otimes {|\psi \rangle }_B={\displaystyle \sum _{k\mathrm{,}j}}{\omega }_{kj}\cdot {|k\rangle }_A\otimes {|j\rangle }_B\mathrm{<mi>\; </mi>}\in {\mathcal{H}}_A\otimes {\mathcal{H}}_B\mathrm{.}$

Generalization of the 2D quantum-computational SMT category $ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_2$ to a large-scale SMT category $ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N$, in which the quantum-computational fusion is called the quantum neural network (QNN, which can be promoted into a “quantum brain” if its dimension N is very large; see [23] ), is defined by the HD tensoring functor, $\otimes \mathrm{<mo>\; :\; </mo>}ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N\times ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N\to ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N$, given by:

$\text{Ob}\left(ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N\right)\mathrm{<mo>\; :\; </mo>}\left\{{\mathcal{H}}_{ij}\mathrm{,}{\mathcal{H}}_{km}\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}{\mathcal{H}}_{ij}\otimes {\mathcal{H}}_{km}\equiv {\mathcal{H}}_{km}\otimes {\mathcal{H}}_{ij}\mathrm{,}\left(\text{allindices}=\mathrm{1,}\cdots \mathrm{,}N\right)\mathrm{,}$

$\text{Mor}\left(ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N\right)\mathrm{<mo>\; :\; </mo>}\left\{{\mathcal{H}}_{ij}\stackrel{f}{\to }{\mathcal{H}}_{km}\mathrm{,}{\mathcal{H}}_{pq}\stackrel{g}{\to }{\mathcal{H}}_{rs}\right\}\mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}{\mathcal{H}}_{ij}\otimes {\mathcal{H}}_{km}f\otimes g{\mathcal{H}}_{pq}\otimes {\mathcal{H}}_{rs}\mathrm{,}$

with objects given by the following ( $N\times N$ )-matrix of Hilbert spaces:

${\left(\mathcal{H}\right)}_{NN}=\left[\begin{array}{cccccccccc}{\mathcal{H}}_{11}& \otimes & {\mathcal{H}}_{12}& \otimes & {\mathcal{H}}_{13}& \otimes & \cdots & \otimes & \cdots & {\mathcal{H}}_{1N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ {\mathcal{H}}_{21}& \otimes & {\mathcal{H}}_{22}& \otimes & {\mathcal{H}}_{23}& \otimes & \cdots & \otimes & \cdots & {\mathcal{H}}_{2N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ {\mathcal{H}}_{31}& \otimes & {\mathcal{H}}_{32}& \otimes & {\mathcal{H}}_{33}& \otimes & \cdots & \otimes & \cdots & {\mathcal{H}}_{3N}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ {\mathcal{H}}_{N1}& \otimes & {\mathcal{H}}_{N2}& \otimes & {\mathcal{H}}_{N3}& \otimes & \cdots & \otimes & \cdots & {\mathcal{H}}_{NN}\end{array}\right]\in ℌ\mathfrak{i}\mathfrak{l}{\mathfrak{b}}_N\mathrm{.}$ (1)

Every element in the matrix (1) represents the Hilbert state-space of a single multiqubit circuit with its own quantum state: ${|\psi \rangle }_{kk}\in {\mathcal{H}}_{kk}$ (for $k=1,\cdots ,N$ ) so that all quantum states form the corresponding complex-valued ( $N\times N$ )-matrix, in which every tensor product ${\otimes }_{kj}\in {\left(|\psi \rangle \right)}_{NN}$ has its associated weight matrix ${\left(\omega \right)}_{kj}\in ℂ$ (see [6] ):

${\left(|\psi \rangle \right)}_{NN}=\left[\begin{array}{cccccccccc}{|\psi \rangle }_{11}& \otimes & {|\psi \rangle }_{12}& \otimes & {|\psi \rangle }_{13}& \otimes & \cdots & \otimes & \cdots & {|\psi \rangle }_{1N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ {|\psi \rangle }_{21}& \otimes & {|\psi \rangle }_{22}& \otimes & {|\psi \rangle }_{23}& \otimes & \cdots & \otimes & \cdots & {|\psi \rangle }_{2N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ {|\psi \rangle }_{31}& \otimes & {|\psi \rangle }_{32}& \otimes & {|\psi \rangle }_{33}& \otimes & \cdots & \otimes & \cdots & {|\psi \rangle }_{3N}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ {|\psi \rangle }_{N1}& \otimes & {|\psi \rangle }_{N2}& \otimes & {|\psi \rangle }_{N3}& \otimes & \cdots & \otimes & \cdots & {|\psi \rangle }_{NN}\end{array}\right]\in {\left(\mathcal{H}\right)}_{NN}\mathrm{.}$ (2)

3. The Entangled Warfare Category

Now, inspired by the QNN model (1)-(2), we can introduce our main result, the HD warfare-category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ ―as a tensor entanglement of all existing Red and Blue battle-manifolds¹²:

$\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}=M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}\mathrm{.}$

Specifically, the objects and morphisms of the $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ -category are defined by the action of the HD warfare tensoring functor, $\otimes \mathrm{<mo>\; :\; </mo>}\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\times \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\to \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$, given by:

$\begin{array}{l}\text{Ob}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\right)\mathrm{<mo>\; :\; </mo>}\left\{\left[M_{\text{Red}}^{ij}\otimes M_{\text{Blue}}^{ij}\right]\mathrm{,}\left[M_{\text{Red}}^{km}\otimes M_{\text{Blue}}^{km}\right]\right\}\\ \mathrm{<mi>\; </mi>}\mapsto \mathrm{<mi>\; </mi>}\left[M_{\text{Red}}^{ij}\otimes M_{\text{Blue}}^{ij}\right]\otimes \left[M_{\text{Red}}^{km}\otimes M_{\text{Blue}}^{km}\right]\mathrm{,}\end{array}$

$\begin{array}{l}\text{Mor}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\right)\mathrm{<mo>\; :\; </mo>}\{\left[M_{\text{Red}}^{ij}\otimes M_{\text{Blue}}^{ij}\right]\stackrel{f}{\to }\left[M_{\text{Red}}^{km}\otimes M_{\text{Blue}}^{km}\right]\mathrm{,}\\ \left[M_{\text{Red}}^{pq}\otimes M_{\text{Blue}}^{pq}\right]\stackrel{g}{\to }\left[M_{\text{Red}}^{rs}\otimes M_{\text{Blue}}^{rs}\right]\}\\ \mapsto \mathrm{<mi>\; </mi>}\left[M_{\text{Red}}^{ij}\otimes M_{\text{Blue}}^{ij}\right]\otimes \left[M_{\text{Red}}^{km}\otimes M_{\text{Blue}}^{km}\right]f\\ \otimes g\left[M_{\text{Red}}^{pq}\otimes M_{\text{Blue}}^{pq}\right]\otimes \left[M_{\text{Red}}^{rs}\otimes M_{\text{Blue}}^{rs}\right]\end{array}$

(with all indices going from $\mathrm{1,}\cdots \mathrm{,}N$ ).

In the warfare-category: $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}=M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}$, the sub-objects $M_{\text{Red}}^{NN}$ and $M_{\text{Blue}}^{NN}$ are represented by the following (N, N)-matrices of Red and Blue battle-manifolds, respectively:

$M_{\text{Red}}^{NN}=\left[\begin{array}{cccccccccc}{M}_{\text{Red}}^{11}& \otimes & M_{\text{Red}}^{12}& \otimes & M_{\text{Red}}^{13}& \otimes & \cdots & \otimes & \cdots & M_{\text{Red}}^{1N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ M_{\text{Red}}^{21}& \otimes & M_{\text{Red}}^{22}& \otimes & M_{\text{Red}}^{23}& \otimes & \cdots & \otimes & \cdots & M_{\text{Red}}^{2N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ M_{\text{Red}}^{31}& \otimes & M_{\text{Red}}^{32}& \otimes & M_{\text{Red}}^{33}& \otimes & \cdots & \otimes & \cdots & M_{\text{Red}}^{3N}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ M_{\text{Red}}^{N1}& \otimes & M_{\text{Red}}^{N2}& \otimes & M_{\text{Red}}^{N3}& \otimes & \cdots & \otimes & \cdots & M_{\text{Red}}^{NN}\end{array}\right]\in \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ (3)

and

$M_{\text{Blue}}^{NN}=\left[\begin{array}{cccccccccc}{M}_{\text{Blue}}^{11}& \otimes & M_{\text{Blue}}^{12}& \otimes & M_{\text{Blue}}^{13}& \otimes & \cdots & \otimes & \cdots & M_{\text{Blue}}^{1N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ M_{\text{Blue}}^{21}& \otimes & M_{\text{Blue}}^{22}& \otimes & M_{\text{Blue}}^{23}& \otimes & \cdots & \otimes & \cdots & M_{\text{Blue}}^{2N}\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ M_{\text{Blue}}^{31}& \otimes & M_{\text{Blue}}^{32}& \otimes & M_{\text{Blue}}^{33}& \otimes & \cdots & \otimes & \cdots & M_{\text{Blue}}^{3N}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ M_{\text{Blue}}^{N1}& \otimes & M_{\text{Blue}}^{N2}& \otimes & M_{\text{Blue}}^{N3}& \otimes & \cdots & \otimes & \cdots & M_{\text{Blue}}^{NN}\end{array}\right]\in \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\mathrm{.}$ (4)

In the matrices of battle-manifolds (3)-(4) the corresponding Red and Blue vectorfields, $R_{ik}^a$ and $B_{ik}^a$ $\left(i,k=1,\cdots ,N\right)$, are acting in their respective battle-manifolds:

$R_{NN}^a=R_{NN}^a\left(x\mathrm{,}t\right)=\left[\begin{array}{cccccccccc}{R}_{11}^a& \otimes & R_{12}^a& \otimes & R_{13}^a& \otimes & \cdots & \otimes & \cdots & R_{1N}^a\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ R_{21}^a& \otimes & R_{22}^a& \otimes & R_{23}^a& \otimes & \cdots & \otimes & \cdots & R_{2N}^a\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ R_{31}^a& \otimes & R_{32}^a& \otimes & R_{33}^a& \otimes & \cdots & \otimes & \cdots & R_{3N}^a\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ R_{N1}^a& \otimes & R_{N2}^a& \otimes & R_{N3}^a& \otimes & \cdots & \otimes & \cdots & R_{NN}^a\end{array}\right]\in M_{\text{Red}}^{NN}\mathrm{,}$ (5)

and

$B_{NN}^a=B_{NN}^a\left(x\mathrm{,}t\right)=\left[\begin{array}{cccccccccc}{B}_{11}^a& \otimes & B_{12}^a& \otimes & B_{13}^a& \otimes & \cdots & \otimes & \cdots & B_{1N}^a\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ B_{21}^a& \otimes & B_{22}^a& \otimes & B_{23}^a& \otimes & \cdots & \otimes & \cdots & B_{2N}^a\\ \otimes & \cdots & \otimes & \cdots & \otimes & \cdots & \cdots & \cdots & \cdots & \otimes \\ B_{31}^a& \otimes & B_{32}^a& \otimes & B_{33}^a& \otimes & \cdots & \otimes & \cdots & B_{3N}^a\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ B_{N1}^a& \otimes & B_{N2}^a& \otimes & B_{N3}^a& \otimes & \cdots & \otimes & \cdots & B_{NN}^a\end{array}\right]\in M_{\text{Blue}}^{NN}\mathrm{.}$ (6)

In the matrices (5)-(6), the Red and Blue vectorfields, $R_{ik}^a$ and $B_{ik}^a$ (for and $a=1,\cdots ,n$ ), are governed by the HD generalization of the standard TCW-combat equations:

${\partial }_t{R}_{ik}^a=k{A}_b^a{B}_{ik}^b+k_b{F}_{cd}^{ab}{R}_{ik}^c{B}_{ik}^d+R_{ik}^b{\mathcal{L}}_R{\mathcal{N}}_b^a+\left[R_{ik}^a\mathrm{,}{B}_{ik}^a\right]+\delta R_{ik}^a\left(\text{H}-\text{L}\right)\mathrm{,}$ (7)

${\partial }_t{B}_{ik}^a=\kappa C_b^a{R}_{ik}^b+{\kappa }_b{G}_{cd}^{ab}{R}_{ik}^c{B}_{ik}^d+B_{ik}^b{\mathcal{L}}_B{\mathfrak{N}}_b^a+\left[B_{ik}^a\mathrm{,}{R}_{ik}^a\right]+\delta B_{ik}^a\left(\text{H}-\text{L}\right)\mathrm{,}$

where $i,k=1,\cdots ,N$ ( $N=\dim$ of the $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ -category, i.e. the number of entangled battle-manifolds $M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}$, for simplicity equal to N for both Red and Blue warfighting parties); $a=\mathrm{1,}\cdots \mathrm{,}n$ ( $n=\dim$ of each individual battle-manifold, for simplicity equal to n for both $M_{\text{Red}}$ and $M_{\text{Blue}}$ ); $k{A}_b^a{B}^b\in M_{\text{Red}}$ and $\kappa C_b^a{R}^b\in M_{\text{Blue}}$ are linear Lanchester-type terms with combat tensors $A_b^a$ and $C_b^a$ ; $k_b{F}_{cd}^{ab}{B}^c{R}^d\in M_{\text{Red}}$ and ${\kappa }_b{G}_{cd}^{ab}{B}^c{R}^d\in M_{\text{Blue}}$ are quadratic Lanchester-type terms with the (strategic, tactical and operational) 4th-order tensors $F_{cd}^{ab}$ and $G_{cd}^{ab}$ ; $R^b{\mathfrak{L}}_R{\mathfrak{N}}_b^a\in M_{\text{Red}}$ and $B^b{\mathfrak{L}}_B{\mathcal{N}}_b^a\in M_{\text{Blue}}$ are entropic Lie-dragging terms; $\left[R^a\mathrm{,}{B}^a\right]\in M_{\text{Red}}$ and $\left[B^a\mathrm{,}{R}^a\right]\in M_{\text{Blue}}$ are entropic Red-Blue commutators; and $\delta R^a\left(\text{H}-\text{L}\right)$ and $\delta B^a\left(\text{H}-\text{L}\right)$ are Hamilton-Langevin delta strikes (for technical details on included tensor terms, see [3] [4] ).

4. Discussion

In summary, by specializing the generic tensoring (bi)functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ into the warfare tensoring functor, $\otimes \mathrm{<mo>\; :\; </mo>}\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\times \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\to \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$, we have developed the global warfare model as the HD entangled warfare category:

$\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\equiv \left[\text{Ob}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\right)\mathrm{,}\text{Mor}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\right)\right]=M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}\mathrm{,}$

in which the two warfighting parties, Red and Blue¹³, include all involved Red-Blue battle-manifolds (3)-(4), in which the action of the corresponding Red-Blue vectorfields (5)-(6) is happening according to the HD combat Equations (7).

Our global warfare model, the $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ -category, has the following main characteristics:

Ÿ $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ includes all interrelated battlefields occurring in an abstract warfare scenario, represented by the entangled fusion, $M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}$ of the Red and Blue matrices of the battle-manifolds (3)-(4);

Ÿ Each individual battlefield is represented by the entangled fusion, $M_{\text{Red}}\otimes M_{\text{Blue}}$, of the individual Red and Blue battle-manifolds, $M_{\text{Red}}$ and $M_{\text{Blue}}$ ;

Ÿ Each individual battlefield, $M_{\text{Red}}\otimes M_{\text{Blue}}$, involves the action of the corresponding Red-Blue vectorfields (5)-(6);

Ÿ The action of all included Red-Blue vectorfields is governed by the HD combat Equations (7).

The (bi) functoriality of the warfare tensoring functor, $\otimes \mathrm{<mo>\; :\; </mo>}\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\times \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\to \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$, can be extended to the case of two major warfighting conflicts, $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_1$ and $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_2$, simultaneously occupying two different parts of the globe and producing the combined output $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}$, as: $\otimes \mathrm{<mo>\; :\; </mo>}\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_1\times \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_2\to \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}$.The objects and morphisms of the combined category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}$ are given by the combined battle manifolds for the Red and Blue warfighting parties, $M_{{\text{R}}_{12}}^{NN}\otimes M_{{\text{B}}_{12}}^{NN}$, as:

$\begin{array}{l}\text{Ob}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}\right)\mathrm{<mo>\; :\; </mo>}\left\{\left[M_{{\text{R}}_{12}}^{ij}\otimes M_{{\text{B}}_{12}}^{ij}\right]\mathrm{,}\left[M_{{\text{R}}_{12}}^{km}\otimes M_{{\text{B}}_{12}}^{km}\right]\right\}\\ \mapsto \mathrm{<mi>\; </mi>}\left[M_{{\text{R}}_{12}}^{ij}\otimes M_{{\text{B}}_{12}}^{ij}\right]\otimes \left[M_{{\text{R}}_{12}}^{km}\otimes M_{{\text{B}}_{12}}^{km}\right]\mathrm{,}\end{array}$

$\begin{array}{l}\text{Mor}\left(\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}\right)\mathrm{<mo>\; :\; </mo>}\{\left[M_{{\text{R}}_{12}}^{ij}\otimes M_{{\text{B}}_{12}}^{ij}\right]\stackrel{f}{\to }\left[M_{{\text{R}}_{12}}^{km}\otimes M_{{\text{B}}_{12}}^{km}\right]\mathrm{,}\\ \left[M_{{\text{R}}_{12}}^{pq}\otimes M_{{\text{B}}_{12}}^{pq}\right]\stackrel{g}{\to }\left[M_{{\text{R}}_{12}}^{rs}\otimes M_{{\text{B}}_{12}}^{rs}\right]\}\mathrm{<mi>\; </mi>}\\ \mapsto \mathrm{<mi>\; </mi>}\left[M_{{\text{R}}_{12}}^{ij}\otimes M_{{\text{B}}_{12}}^{ij}\right]\otimes \left[M_{{\text{R}}_{12}}^{km}\otimes M_{{\text{B}}_{12}}^{km}\right]f\\ \otimes g\left[M_{{\text{R}}_{12}}^{pq}\otimes M_{{\text{B}}_{12}}^{pq}\right]\otimes \left[M_{{\text{R}}_{12}}^{rs}\otimes M_{{\text{B}}_{12}}^{rs}\right]\end{array}$

with the subsequent extension of the manifold matrices (3)-(4), vectorfields (5)-(6) and combat Equations (7).

The extended warfare (bi)category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}{\mathfrak{e}}_{12}$ shows that whenever there are two apparently unrelated warfighting conflicts in different parts of the world (e.g., on different continents)-ultimately they would be entangled into the same global warfare. In other words, even though we have two geographically-separated conflicts, the proposed framework suggests that they can be linked through entanglement fusion.

The concept of Global Warfare was illustrated in this section and we have shown a practical approach to the holistic modeling of warfare. The framework illustrated here has clearly allowed for the capture of the complexity of the Global Warfare through the use of the concept of entanglement.

We are confident that this framework is appropriate for the evaluation of future force structures, capability, strategies and tactics. As a result our approach may be thought of as a tool to aid the future planning and design process, being incorporated in such work-flow by the military. We have been successful in creating a formal mathematical framework through the utility of Tensors and the concept of entanglement to capture this global view of warfare.

5. Conclusions

In this paper we have proposed a global warfare model, represented by the high-dimensional entangled category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$.The metaphysics of this global warfare model is “entangled fusion”, the macroscopic entanglement concept, inspired by high-dimensional (HD) quantum computation (the “quantum brain”) in which any number of entangled wave-functions can be highly-correlated, with neuron-like signaling among them. In this “entangled view”, the warfare is essentially a holistic phenomenon, thus if any one of mutually entangled warfighting parties is removed from the equation, the conflict, in its present form, instantly stops, though possibly being instantly replaced by another.

This delineation of conflicts within our global entangled model thus ascribes a different identity to distinct phases or threads within a larger surrounding web of conflict, as parties enter or exit different states of conflict or cooperation with other parties. We believe this more accurately reflects the way in which past and present geopolitical conflict manifests; in particular, our model here is intended to represent war and battle more from a national perspective, rather than from the point of view of isolated individual battles or missions temporally linearly arranged.

As an integration of the whole tensor centric warfare series, the formal global warfare framework developed in this paper expresses this fundamental idea of many simultaneously interrelated/entangled battlefields, each of them defined by its own battle-manifold (with warfighting tensor fields actin on it) and occurring (more-or-less) simultaneously on the planet which is called the entangled category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$.The action of the $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ -category is formally defined using the warfare tensoring (bi) functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\times \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}\to \mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$.

We are confident that the framework presented here is appropriate for the evaluation of future force structures, capability, strategies and tactics, and can be used as a tool to aid the future planning and design process, incorporating a holistic work-flow for the military. We have been successful in creating a formal mathematical framework through the utility of Tensors and the concept of entanglement to capture this global view of warfare.

Acknowledgements

The authors are grateful to Dr. Tim McKay, Joint and Operations Analysis Division, Defence Science & Technology Group, Australia-for his support of the research work presented in this paper.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Ivancevic, V., Reid, D., Pourbeik, P. and Pilling, M. (2019) Tensor-Centric Warfare VI: A Global Warfare Model. Intelligent Control and Automation, 10, 46-61. https://doi.org/10.4236/ica.2019.101003

References

Appendix: Basic Categories and Functors

Here we give a very brief introduction to standard category theory (the principal reference is [12]; for a simplified exposition, see e.g. [18]).

A category is a generic mathematical structure consisting of two collections: 1) a collection of objects (sets with some additional structure), and 2) the corresponding collection of morphisms (or, arrows) between objects (agreeing with this additional structure). A category $\mathcal{C}$ is defined as a pair $\left(\text{Ob}\left(\mathcal{C}\right)\mathrm{,}\text{Mor}\left(\mathcal{C}\right)\right)$ of generic objects $A\mathrm{,}B\mathrm{,}\cdots$ in $\text{Ob}\left(\mathcal{C}\right)$ and generic morphisms $f\mathrm{<mo>\; :\; </mo>}A\to B\mathrm{,}g\mathrm{<mo>\; :\; </mo>}B\to C\mathrm{,}\cdots$ in $\text{Mor}\left(\mathcal{C}\right)$ between objects, with associative composition:

$A\to B\to C=A\to C,$

and identity (loop) morphism¹⁴.

A category $\mathcal{C}$ is usually visualized as a commutative diagram:

To make this more precise, we say that a category $\mathcal{C}$ is defined if we have:

1) A class of objects $\left\{A\mathrm{,}B\mathrm{,}C\mathrm{,}\cdots \right\}$ of $\mathcal{C}$, denoted by $\text{Ob}\left(\mathcal{C}\right)$ ;

2) A class of arrows, or morphisms ${\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)$, with elements $f\mathrm{<mo>\; :\; </mo>}A\to B$, defined for any ordered pair of objects $\left(A\mathrm{,}B\right)\in \text{Ob}\left(\mathcal{C}\right)$, such that for two different pairs $\left(A\mathrm{,}B\right)\ne \left(C\mathrm{,}D\right)$ in $\mathcal{C}$, we have ${\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)\cap {\text{Mor}}_{\mathcal{C}}\left(C\mathrm{,}D\right)=\varnothing$ ;

3) For any triplet $\left(A\mathrm{,}B\mathrm{,}C\right)\in \text{Ob}\left(\mathcal{C}\right)$ with $f\mathrm{<mo>\; :\; </mo>}A\to B$ and $g\mathrm{<mo>\; :\; </mo>}B\to C$, there is a composition of morphisms

${\text{Mor}}_{\mathcal{C}}\left(B\mathrm{,}C\right)\times {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)∍\left(g\mathrm{,}f\right)\to g\circ f\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}C\right)\mathrm{,}$

written schematically in the standard logic form:

$\frac{f\mathrm{<mo>\; :\; </mo>}A\to B\mathrm{,}g\mathrm{<mo>\; :\; </mo>}B\to C}{g\circ f\mathrm{<mo>\; :\; </mo>}A\to C}\mathrm{.}$

Recall from above that if we have a morphism $f\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)$, then $A=\text{dom}\left(f\right)$ is a domain of f, and $B=\text{cod}\left(f\right)$ is a codomain of f (of which range of f is a subset, $B=\text{ran}\left(f\right)$ ).

To make $\mathcal{C}$ a category, it must also fulfill the following two properties:

1) Associativity of morphisms: for all $f\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)$, $g\in {\text{Mor}}_{\mathcal{C}}\left(B\mathrm{,}C\right)$, and $h\in {\text{Mor}}_{\mathcal{C}}\left(C\mathrm{,}D\right)$, we have $h\circ \left(g\circ f\right)=\left(h\circ g\right)\circ f$ ; in other words, the following diagram is commutative

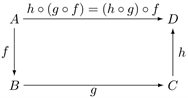
2) Existence of identity morphism: for every object $A\in \text{Ob}\left(\mathcal{C}\right)$ there exists a unique identity morphism $1_A\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}A\right)$ ; for any two morphisms $f\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)$, and $g\in {\text{Mor}}_{\mathcal{C}}\left(B\mathrm{,}C\right)$, compositions with identity morphism $1_B\in {\text{Mor}}_{\mathcal{C}}\left(B\mathrm{,}B\right)$ give $1_B\circ f=f$ and $g\circ 1_B=g$, i.e., the following diagram is commutative:

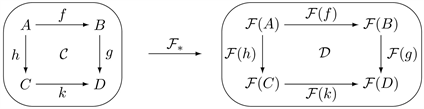
A functor is a generic picture, projecting (all objects and morphisms of) a source category into (corresponding objects and morphisms of) a target category. Let $\mathcal{C}=\left(\text{Ob}\left(\mathcal{C}\right)\mathrm{,}\text{Mor}\left(\mathcal{C}\right)\right)$ be a source (or, domain) category and $\mathcal{D}=\left(\text{Ob}\left(\mathcal{D}\right)\mathrm{,}\text{Mor}\left(\mathcal{D}\right)\right)$ be a target (or, codomain) category. A functor $\mathcal{F}=\left({\mathcal{F}}_O\mathrm{,}{\mathcal{F}}_M\right)$ is defined as a pair of maps, ${\mathcal{F}}_O\mathrm{<mo>\; :\; </mo>}\text{Ob}\left(\mathcal{C}\right)\to \text{Ob}\left(\mathcal{D}\right)$ and ${\mathcal{F}}_M\mathrm{<mo>\; :\; </mo>}\text{Mor}\left(\mathcal{C}\right)\to \text{Mor}\left(\mathcal{D}\right)$, preserving categorical symmetry (i.e., commutativity of all diagrams) of $\mathcal{C}$ in $\mathcal{D}$.

Slightly more precisely, a covariant functor, or simply a functor ${\mathcal{F}}_{\ast }\mathrm{<mo>\; :\; </mo>}\mathcal{C}\to \mathcal{D}$ is a picture in the target category $\mathcal{D}$ of (all objects and morphisms of) the source category $\mathcal{C}$ :

Similarly, a contravariant functor, or a cofunctor ${\mathcal{F}}^{\ast }\mathrm{<mo>\; :\; </mo>}\mathcal{C}\to \mathcal{D}$ is a dual picture with reversed arrows in the target category

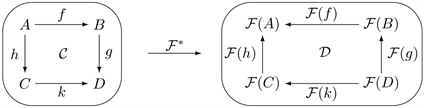
In other words, a functor $\mathcal{F}\mathrm{<mo>\; :\; </mo>}\mathcal{C}\to \mathcal{D}$ from a source category $\mathcal{C}$ to a target category $\mathcal{D}$ is a pair $\mathcal{F}=\left({\mathcal{F}}_O\mathrm{,}{\mathcal{F}}_M\right)$ of maps, ${\mathcal{F}}_O\mathrm{<mo>\; :\; </mo>}\text{Ob}\left(\mathcal{C}\right)\to \text{Ob}\left(\mathcal{D}\right)$, ${\mathcal{F}}_M\mathrm{<mo>\; :\; </mo>}\text{Mor}\left(\mathcal{C}\right)\to \text{Mor}\left(\mathcal{D}\right)$, such that the following holds:

1) If $f\in {\text{Mor}}_{\mathcal{C}}\left(A\mathrm{,}B\right)$ then ${\mathcal{F}}_M\left(f\right)\in {\text{Mor}}_{\mathcal{D}}\left({\mathcal{F}}_O\left(A\right)\mathrm{,}{\mathcal{F}}_O\left(B\right)\right)$ in case of the covariant functor ${\mathcal{F}}_{\ast }$, and ${\mathcal{F}}_M\left(f\right)\in {\text{Mor}}_{\mathcal{D}}\left({\mathcal{F}}_O\left(B\right)\mathrm{,}{\mathcal{F}}_O\left(A\right)\right)$ in case of the contravariant functor ${\mathcal{F}}^{\ast }$ ;

2) For all $A\in \text{Ob}\left(\mathcal{C}\right)$ : ${\mathcal{F}}_M\left(1_A\right)=1_{{\mathcal{F}}_O\left(A\right)}$ ;

3) For all $f\mathrm{,}g\in \text{Mor}\left(\mathcal{C}\right)$ : if $\text{cod}\left(f\right)=\text{dom}\left(g\right)$, then ${\mathcal{F}}_M\left(g\circ f\right)={\mathcal{F}}_M\left(g\right)\circ {\mathcal{F}}_M\left(f\right)$ in case of the covariant functor ${\mathcal{F}}_{\ast }$, and ${\mathcal{F}}_M\left(g\circ f\right)={\mathcal{F}}_M\left(f\right)\circ {\mathcal{F}}_M\left(g\right)$ in case of the contravariant functor ${\mathcal{F}}^{\ast }$.

For further details, see [12] [18].

NOTES

¹The general concept of entanglement subsumes three fundamental scientific concepts: correlation, causality and function between two systems or processes (see [6] ). Its micro + macro nature is arguably best defined by the popular “second Einstein equation” (coined by L. Susskind from Stanford and J. Maldacena from Princeton): $ER=EPR\mathrm{<mi>\; </mi>\; <mi>\; </mi>}\stackrel{\text{or}}{\iff }\mathrm{<mi>\; </mi>\; <mi>\; </mi>}Wormhole=Entanglement\mathrm{,}$ which relates two Einstein’s papers from 1935: ER, referring to the Einstein-Rosen bridge [7] (or, a cosmological wormhole that connects two distant parts of the universe); and EPR, referring to the Einstein, Podolsky and Rosen paradox [8] in which the entanglement was born as a quantum non-locality (to be three decades later governed by Bell’s theorem; see [9] and the references therein).

²The Cartesian product, $X\times Y$, of two sets, X and Y, consists of all ordered pairs $\left(x\mathrm{,}y\right)$ of the elements $x\in X$ and $y\in Y$.It can be generalized (lifted/abstracted) to the notion of a “tensoring functor” because it applies suitably both to the sets and to the functions between them.

³For example, in a simple quantum computation involving only two qubits, the Bell states represent four maximally-entangled quantum states of the qubits. Generalization to any number of multicubits (or, n-cubits) is straightforward, and the degree of entanglement is measured by the von Neumann entropy: $S=-\text{Tr}\left(\rho \ln \rho \right)$, where $\rho$ is the density matrix that describes a quantum system in a mixed state (a statistical ensemble of several states).

⁴The fundamental phenomenon of entanglement arises in compound quantum systems defined by tensor products of their component systems. The general form of a vector ${|\psi \rangle }_i\otimes {|\psi \rangle }_k$ in ${\mathcal{H}}_i\otimes {\mathcal{H}}_k$ may encode high correlations between the first and second components and cannot simply be resolved into a pair of vectors ${|\psi \rangle }_i$ and ${|\psi \rangle }_k$ in the component spaces ${\mathcal{H}}_i$ and ${\mathcal{H}}_k$.

⁵All quantum-computational processes Q (including: quantum information-flow, teleportation, entanglement swapping and communication protocols, as well as quantum cryptography, games and gambling (see [10] [11] and the references therein)-are naturally occurring between two quantum state-agents, traditionally called Alice (A) and Bob (B). In this paper, we generalize this Alice--Bob metaphor to arbitrary interacting CPC-systems.

⁶The simplest way of thinking of the parallel/spatial composition (entangled fusion) is juxtaposition: putting two (or, several) systems side-by-side to make them act as one (a coherent pair or team). However, from the “second Einstein’s equation” it follows that the entangled systems can be non-local, i.e., physically separated by large distances, e.g. situated on different continents, like a mother and daughter, or twin siblings and yet fully entangled and functioning as a coherent one system.

⁷A monoid is a category with one object, which is a group without inverses (a group is a category with one object in which all morphisms are isomorphisms).

⁸For technical details, see MacLane’s Coherence Conditions, theorem XI.1.1 in [12] ; for non-technical introduction, see [13] [14] .

⁹This implies that the SMT category $\mathcal{C}$ is not an ordinary category, but rather Bénabou’s bicategory [16] [17] , which also includes an identity object 1 and some natural isomorphisms obeying MacLane’s coherence conditions [12] , including the fancy “pentagon” diagram. In the bicategory $\mathcal{C}$, the usual categorical composition $\circ$ is naturally used to represent physical processes combined in series, while the tensoring $\otimes$ represents physical processes combined in parallel. A bifunctor is a generic picture projecting (all objects and morphisms of) a source bicategory into a target bicategory. Our tensoring functor $\otimes \mathrm{<mo>\; :\; </mo>}\mathcal{C}\times \mathcal{C}\to \mathcal{C}$ is technically a bifunctor. For a “readable” introduction to HD categories (or, n-categories), see [18] and the references therein.

¹⁰Open CPC-systems exchange energy/information with their environments.

¹¹Technically speaking, a class of quantum circuits that is closed under both $\otimes$ and $\circ$ is the class of Clifford stabilizer circuits (see, e.g. [19] [20] [21] [22] ).

¹²The two party warfare-category $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ can be easily generalized to three or more entangled parties: $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}=M_{\text{Red}}^{NN}\otimes M_{\text{Blue}}^{NN}\otimes M_{\text{Green}}^{NN}\otimes \cdot \cdot \cdot$.

¹³As noted before, the $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ -category is the flexible architecture which is not restricted to Red vs. Blue warfare, but can include any number p of warfighting parties, in such a way that all tensor products in $\mathfrak{W}\mathfrak{a}\mathfrak{r}\mathfrak{f}\mathfrak{a}\mathfrak{r}\mathfrak{e}$ would have p entangled components.

¹⁴In topological literature, $\text{Hom}\left(\mathcal{C}\right)$ or $\text{hom}\left(\mathcal{C}\right)$ is used instead of $\text{Mor}\left(\mathcal{C}\right)$ ; see [12] [24].