Intelligent Control and Automation
Vol.07 No.02(2016), Article ID:66468,16 pages
10.4236/ica.2016.72005
Estimation of Decision Alternatives on the Basis of Interval Pairwise Comparison Matrices
Nataliya D. Pankratova, Nadezhda I. Nedashkovskaya
Institute for Applied Systems Analysis, National Technical University of Ukraine “Kyiv Polytechnic Institute”, Kyiv, Ukraine

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 March 2016; accepted 13 May 2016; published 16 May 2016
ABSTRACT
This paper deals with the calculation of a vector of reliable weights of decision alternatives on the basis of interval pairwise comparison judgments of experts. These weights are used to construct the ranking of decision alternatives and to solve selection problems, problems of ratings construction, resources allocation problems, scenarios evaluation problems, and other decision making problems. A comparative analysis of several popular models, which calculate interval weights on the basis of interval pairwise comparison matrices (IPCMs), was performed. The features of these models when they are applied to IPCMs with different inconsistency levels were identified. An algorithm is proposed which contains the stages for analyzing and increasing the IPCM inconsistency, calculating normalized interval weights, and calculating the ranking of decision alternatives on the basis of the resulting interval weights. It was found that the property of weak order preservation usually allowed identifying order-related intransitive expert pairwise comparison judgments. The correction of these elements leads to the removal of contradictions in resulting weights and increases the accuracy and reliability of results.
Keywords:
Interval Pairwise Comparison Matrix, Interval Weights, Weakly Consistent Interval Expert Judgments, Intransitive Interval Expert Judgments, Consistency Increasing of Interval Expert Judgments, Weak and Strong Order Preservation

1. Introduction
The problem of calculation of weights of decision alternatives using methods of pairwise comparisons is considered for the case when the initial information is provided in the form of assessments given by experts or decision makers. In recent years, fuzzy pairwise comparisons methods that use expert judgments in the form of fuzzy pairwise comparison matrices (PCMs) [1] and interval PCMs [2] - [8] became widespread. Calculated weights are further used to construct the ranking of decision alternatives and to solve the following problems: selection problems, problems of ratings construction, resources allocation problems, scenarios evaluation problems, and other decision making problems.
To calculate weights of decision alternatives on the basis of an Interval PCM (IPCM)
 , several models have been developed such as FPP [2] , GPM [3] [4] ,
, several models have been developed such as FPP [2] , GPM [3] [4] ,
LUAM [5] , MFLLSM [6] , two-stage models TLGP [7] and 2SLGP [8] , and others. The FPP model calculates crisp weights and requires additional parameters that characterize the personal qualities of an expert. The MFLLSM and TLGP models require solving nonlinear mathematical programming problems. Chang’s method [9] of calculating weights based on fuzzy PCM with triangular fuzzy numbers
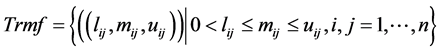 is used. However, in conventional models, little attention
is used. However, in conventional models, little attention
is given to the issues of consistency of interval and fuzzy PCMs. The above-mentioned models cannot determine whether the IPCM inconsistency is acceptable for the decision-making process. The authors do not offer methods to increase the consistency of interval and fuzzy PCMs.
The purpose of this paper is to calculate a reliable interval weight vector on the basis of IPCMs with different inconsistency levels. To achieve this goal, a comparative analysis of several models that calculate interval weights on the basis of IPCM is performed. Resulting interval weights, in our opinion, are more preferable in comparison with crisp weights, because interval weights retain more information from the original IPCM. To find the intransitive IPCM elements that lead to a significant inconsistency of this matrix, the properties of the weak and strong order preservation on the set of decision alternatives are investigated. An algorithm is proposed that analyzes and increases the IPCM consistency, calculates normalized interval weights, and calculates the ranks of decision alternatives on the basis of the resulting interval weights.
2. Problem Statement
Let us consider a positive inverse-symmetric interval pairwise comparison matrix (IPCM):
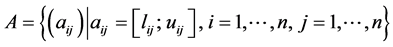 , (1)
, (1)
where ,
, 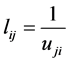 ,
, 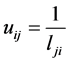 ,
, 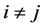 and
and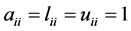 .
.
The problem is to find the vector of interval weights 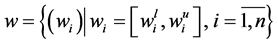 on the basis of an
on the basis of an
IPCM A(1).
3. An Algorithm for Calculating a Vector of Interval Weights on the Basis of IPCM
Let us assume that it is necessary to calculate the relative importance coefficients (weights) of n decision alternatives when the input data are expert pairwise comparison judgments of these alternatives. An expert provides verbal preference assessments for every pair of alternatives. Based on these results, the IPCM (1) is constructed. An algorithm is proposed for calculating the weights of decision alternatives which contains the stages for analyzing the quality of expert judgments, finding the normalized interval weights, and ranking of decision alternatives on the basis of the resulting interval weights (Figure 1).
The quality analysis of expert judgments includes an assessment of a consistency of IPCM and an acceptable inconsistency of an IPCM similarly to the crisp pairwise comparison matrix. It is known that the calculation of weights on the basis of expert pairwise comparison judgments is justified only in case of acceptable inconsistency of these judgments [10] . The best way of increasing the IPCM consistency, in our opinion, is to organize a feedback with an expert, especially in practical problems when an expert is the only source of knowledge. When a feedback with an expert is not possible for some reasons, IPCM elements are automatically changed to increase the consistency without expert’s participation.
Figure 1. The flow chart of the algorithm for evaluating decision alternatives on the basis of an IPCM.
Normalized weights of alternatives corresponding to each criterion are often used while solving multi-criteria decision-making problems. Therefore, the algorithm includes the step of normalization of interval weights, calculated on the basis of an IPCM. Interval weights also require special ranking methods to select the best decision alternative, to construct ratings, and to solve other problems of ordering decision alternatives according to their importance.
Let us consider the steps of the algorithm in more details (see Figure 1).
3.1. IPCM Consistency Estimating
The notion of the consistency is used to assess the contradictoriness level of expert pairwise comparison judgments when calculating weights. Recently, several definitions of a consistent IPCM have been suggested and their comparative analysis has been performed in [11] . In this paper, we use the relatively weak definition (Definition 1). On the basis of this definition, several models of calculating interval weights were proposed [3] - [5] . They will be studied in this paper.
Definition 1. IPCM (1) is consistent if the following acceptable domain is not empty [2] - [8]
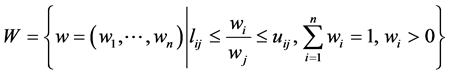 .
.
Statement 1. IPCM (1) is consistent if and only if its elements satisfy the following condition:
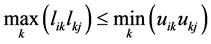 for
for ,
, .
.
In general, an IPCM (1), based on expert judgments, is not consistent. Expert judgments may contain outliers and be intransitive. This leads to the significant inconsistency of an IPCM. Methods for identifying outliers and intransitive elements in a crisp PCM were developed [12] - [14] . These methods, in principle, can be also used in the case of an IPCM. To assess the quality of a crisp PCM, the concept of weak consistency can be used as well [12] [15] .
Let us consider the property of weak consistency of a PCM and the properties of the weak and strong order preservation on the set of decision alternatives; also, let us perform their generalization to the case of IPCM. These properties are used in the paper during the analysis of features of the models for calculating weights.
Definition 2. IPCM (1) is called weakly (ordinally) consistent if the ordinal transitivity takes place [12] [13] [15] :
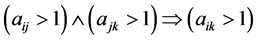 ,
, 

A weakly inconsistent IPCM has at least one cycle, which is determined by three indices 



IPCM indicates the violation of the ordinal transitivity on the set of comparable decision alternatives and can be the result of a random expert error when performing pairwise comparisons of alternatives. In most cases, an IPCM with a cycle has a high level of inconsistency and cannot be used to calculate weights.
Definition 3. The order is preserved weakly (there is a predominance of the elements of an IPCM), if [1]

We suggest the hypothesis that the property of the weak order preservation will allow to identify the elements that lead to a cycle (order-related intransitive elements), and, accordingly, to the inconsistency of an IPCM. It
should be noted that the definition 
the condition 





which is not always justified in practice.
Definition 4. The order is preserved strongly (there is a predominance of the rows of an IPCM), if conditions

lead to 
The traditional eigenvector method (EM) and the logarithmic least squares method for calculating weights on the basis of a crisp PCM provide the strong order preservation, but do not provide the weak preservation [10] .
3.2. Interval Weights Ranking
Methods for calculating weights on the basis of fuzzy (or interval) PCM often result in fuzzy (interval) weight vectors. So, for cases described in Definitions 2-4, such as a weak consistent IPCM, the weak order preservation for the fuzzy case, and strong order preservation for the fuzzy case, it is necessary to use the method of comparison of fuzzy numbers, i.e. elements of fuzzy PCM and elements of a fuzzy weights vector. In [16] , the survey was done of methods proposed in 1970-1980 for ranking fuzzy numbers. They include the degree of optimality method and the methods which use the Hamming function, alpha-levels, fuzzy average and spread, proximity to the ideal, centroid index, etc. There are methods of intervals ranking based on comparison of the middles or ends of the intervals [17] . The disadvantage of these methods is that only the partial ranking can be obtained in many cases. The methods of comparing interval numbers that define an optimism index and a degree of preference of one interval number over another from a pessimistic point of view (decision-maker’s aversion to risk) are proposed in [18] . The properties of these methods and formulas for calculating the degrees of preference for the comparison of interval numbers are given in [7] [19] . The method of degrees of preference is easy in use, has the desired properties (in particular, provides a full ranking), and is widely used [7] [19] - [21] .
The method of degrees of preference is used in this study to determine the relationship between interval numbers in cases of a weak consistent IPCM, the weak order preservation, and the strong order preservation (see Definitions 2-4).
Definition 5. Let us suppose that 





The degree of preference has the following properties:
1)
2)

3) 

4) 

5) 

6) Suppose 



The degree of preference 


process.
Note that the formula for calculating the degree of preference (Formula (2)) can be written in the equivalent form:

Definition 5 allows to find the complete ranking of the set of interval numbers
1) Calculate the matrix of the degrees of preference

2) Calculate the generalized value of the preference of an interval number

or 
3) Build the ranking of interval numbers 

3.3. Interval Weights Normalization
Usually, the methods used for the interval weights normalization are based on interval arithmetic. For example, each number is divided by the sum of all interval values with the use of the extended binary operations. Another method is the normalization of the midpoints of the intervals. While selecting a normalization method, it should be taken into account that the use of extended binary operations often results in overly wide intervals; therefore, it is not always justified in practice. In [22] , the failure of traditional normalization methods is shown and a new normalization method of interval and fuzzy variables is proposed. This paper uses the above-mentioned new method.
Let 


Definition 6. A vector of interval weights

and only if it satisfies two following conditions [22] :
1)
2) 


The first condition indicates that the set N is non-empty. This condition can be satisfied if and only if





reachable for at least one vector in N.
Statement 2. A vector of interval weights

according to Definition 6 if and only if [22] :


Note that the two conditions in statement 2 can be simplified and rewritten in the equivalent form:


Let us consider the GPM [3] [4] and LUAM [5] models for calculating normalized, in accordance with the Definition 6, interval weights based on an IPCM.
4. Models of Interval Weights Calculation on the Basis of an IPCM
4.1. Linear Goal Programming Model (GPM)
IPCM A(1) can be represented by two real positive matrices 




It is known that, for a given by an expert IPCM A(1), there exists a normalized vector





Let us consider the consistent IPCM
and present it with two crisp non-negative matrices 



It can be written in the matrix form as


where

Generally, IPCM A(1) is inconsistent, so the Equations (3) for A hold only approximately. Let us introduce deviation vectors:


where

The values


to find a weight vector

model, the first two restrictions are written in accordance with the condition (4). The next two restrictions give the necessary and sufficient conditions for the normalization of the interval weights vector. The next two restrictions define the properties of the weak and strong order preservation. The last two restrictions are the conditions at the lower and upper end points of the interval of the weight and their non-negativity. Since the deviation vectors 











After the model 1 is rewritten by taking into account the change of variables, we have the linear programming model 2 [3] .
For the consistent IPCM, the values of goal functional 

4.2. Lower and Upper Approximation Models (LUAM)
As before, we assume that for IPCM A(1), given by an expert, there is a normalized vector





Two approximations of IPCM A(1), the lower 



where 

Let 

interval arithmetic, we can write the condition (7) in detail as follows:

During the construction of the lower and the upper models, we will seek the greatest lower and smallest upper bounds of the interval of weights endpoints, respectively. We define the lower model [5] as an optimization problem for maximizing the sum of the lengths of interval numbers 

The main goal of the lower model is to find such weights of decision alternatives that the corresponding theoretical (consistent) IPCM puts a lower limit on a given IPCM (1). The most desirable weights are ones with the greatest possible degree of inaccuracy expressed by the width of the interval number. Therefore, the lower model is formulated as a maximization problem. The first two lower model restrictions provide approaching of the corresponding theoretical (consistent) IPCM to a given IPCM (1) from below. The following two restrictions are the necessary and sufficient conditions for the normalization of an interval weight vector. The last two restrictions ensure the correctness of the interval number and its positivity. One of the features of the lower model is that the solution may not exist at a certain level of inconsistency of expert judgments [5] .
The upper model is used to find such weights of decision alternatives that the corresponding theoretical IPCM puts an upper limit on a given IPCM (1). The most desirable are weights with the minimal possible degree of inaccuracy, so the upper model is formulated as a minimization problem. The restrictions of the upper model are similar to the restrictions of the lower model. It can be shown that the upper model always has an optimal solution.
Let us turn to the analysis of the discussed above models to determine the most reliable weights vector.
4.3. A Comparative Analysis of Models for Calculating Interval Weights on the Basis of an IPCM
The models GPM [3] [4] , LUAM [5] , and TLGP [7] are developed for calculating interval weights on the basis of an IPCM, built according to expert judgments using the multiplicative scales. They can be used for both consistent and inconsistent IPCMs and produce the interval weights. The 2SLGP model [8] works only for IPCMs which are consistent in accordance with Definition 1.
The GPM model is the minimization of absolute values of deviations of a given by an expert IPCM from the theoretical IPCM. The TLGP model calculates the weights vector in two steps. At the first step, the sum of non- negative errors in the transformed space of logarithms is minimized; the result of this step is a set of solutions. At the second step, separately for each decision alternative, two problems of nonlinear programming are solved to select from this set of solutions the minimum and maximum weight values that form, respectively, the left and right endpoints of the weight interval. The LUAM model consists of two sub-models―the lower and the upper. As a result, we get two vectors of interval weights that bound the unknown real alternative weights with two theoretical IPCMs from above and below. These results seem to be less suitable for further using, but generally contain solutions of the TLGP and GPM models.
The GPM and LUAM models allow us to determine the normalized interval weights, but the TLGP model does not. The TLGP model works in logarithmic space of weights and uses the inverse transformation. Interval weights, calculated using the TLGP model, require subsequent normalization with the purpose of their further use in solving of a multi-criteria problem. While choosing a method of interval values normalization, it should be taken into account, that using extended binary operations often leads to overly wide resulting intervals; therefore, it is not always justified in practice.
The TLGP model uses only the elements of a triangular part of an IPCM as the initial data; in this case, the results for the upper and lower triangular parts of IPCM are equivalent. The GPM and LUAM models use all elements of an IPCM.
The GPM and LUAM models include solving linear programming problems. Besides, the lower LUAM model does not always have a solution. The existence of the solution in the lower LUAM model depends on the inconsistency level of an IPCM. The TLGP model requires solving nonlinear programming problems.
The GPM and TLGP models, unlike the LUAM, allow to evaluate in some degree an inconsistency of an IPCM (i.e. expert judgments) [23] . The optimal values of objective functions 

The objective function of the GPM model contains the sum of all deviations in the rows of a given IPCM from the theoretical (consistent) IPCM. Therefore, it becomes possible to identify the most inconsistent IPCM element by finding the maximum term in this sum, i.e. the IPCM row that gives the maximum deviation [23] . Then, we can increase the IPCM consistency. For example, we can organize a feed back with an expert and return to him or her the most inconsistent element for review. Note, that the LUAM model does not have this property, does not allow to increase IPCM consistency, and does not allow to exclude cycles (order-related intransitive expert judgments) in this matrix.
The advantages of the GPM model include the possibility to extend this model easily to the case of fuzzy pairwise comparison matrices whose elements are specified, for example, as triangular or trapezoidal fuzzy sets.
5. The Analysis of Models Using Examples of IPCMs of Different Consistency Levels
Example 1: Let us consider the special case of IPCMs―crisp PCMs




In the case of a fully consistent PCM

Table 1. The weights on the basis of a fully consistent PCM
Table 2. The weights on the basis of the weakly consistent PCM
Table 3. The weights on the basis of the weakly inconsistent PCM
In the following Examples 2-4, a weakly consistent IPCM 






Example 2:
Example 3:

Table 4. The weights on the basis of the weakly consistent IPCM
Table 5. (a) The weights on the basis of the weakly inconsistent IPCM




Table 6. (a) The weights on the basis of the weakly inconsistent IPCM




Example 4:
The performed analysis led to the following conclusions:
1) For weakly consistent IPCM (Table 4), the ranking calculated using the GPM model coincided with the ranking using the traditional eigenvector method EM if it was applied to a defuzzified IPCM. The LUAM model can lead to another ranking on the basis of weakly consistent IPCMs (Table 4 and Table 5(b)). We can also argue that the weights calculated by the GPM model on the basis of weakly consistent IPCM basically satisfy the property of the weak order preservation. This, however, is not always true for the weights calculated on the basis of such IPCM using the LUAM model (Table 4).
Table 7. (a) The weights on the basis of the weakly inconsistent IPCM




2) In the case of weakly inconsistent IPCMs, there are no rankings of decision alternatives that can satisfy all the elements of these IPCMs in the sense that 



3) The feature of the LUAM model is that this model results in indistinguishable alternatives; in other words, it leads to identical weights of alternatives (Table 5(a) and Table 6(a)) if an IPCM is weakly inconsistent and has order-related intransitive elements. As a result, the weights, calculated by the LUAM model, satisfy the property of the weak order preservation more often than the weights calculated by the GPM model (Table 5(a) and Table 6(a)).
4) The LUAM lower model had no solutions for all considered weakly inconsistent IPCMs and also for some weakly consistent IPCMs (Examples 3 and 4).
5) The property of the weak order preservation in general allows to identify the order-related intransitive elements of IPCMs. These are the elements that do not satisfy this property. After their correction, the more consistent IPCMs were obtained. It was illustrated by lower values of the inconsistency indices of the GPM and LUAM models in Table 5(b), Table 6(b) and Table 7(b). However, the inconsistency indices of these models do not allow to determine the level of acceptability of the IPCM inconsistency for calculating weights.
In all these examples, corrected IPCMs are weakly consistent. Based on these IPCMs, the rankings derived using the GPM and LUAM models mostly agreed with each other (Table 6(b) and Table 7(b)).
6) Weights calculated by the GPM and LUAM models satisfy the property of the strong order preservation for all IPCMs from Examples 1-4 regardless of the inconsistency level of these matrices.
6. Conclusions
A comparative analysis of the GPM, LUAM and TLGP models, which calculate interval weights on the basis of an interval pairwise comparison matrix, was performed. When these models were applied to IPCMs with different inconsistency levels, these models’ features were identified.
It was established that the property of the weak order preservation usually allowed identifying order-related intransitive elements in weakly inconsistent IPCMs. After their correction, more consistent IPCMs were obtained, which was reflected by lower values of the inconsistency indices of the GPM and LUAM models. The correction of these elements removes contradictions in resulting weights and increases the accuracy and reliability of results.
An algorithm is proposed which contains the stages of analyzing and increasing of an IPCM consistency, calculating normalized interval weights, and calculating the ranking of decision alternatives on the basis of the resulting interval weights.
Cite this paper
Nataliya D. Pankratova,Nadezhda I. Nedashkovskaya, (2016) Estimation of Decision Alternatives on the Basis of Interval Pairwise Comparison Matrices. Intelligent Control and Automation,07,39-54. doi: 10.4236/ica.2016.72005
References
- 1. Pankratova, N.D. and Nedashkovskaya, N.I. (2010) Models and Methods of Analysis of Hierarchies. Theory and Applications. Kiev. (In Ukrainian)
- 2. Mikhailov, L. (2003) Deriving Priorities from Fuzzy Pairwise Comparison Judgements. Fuzzy Sets and Systems, 134, 365-385.
http://dx.doi.org/10.1016/S0165-0114(02)00383-4 - 3. Wang, Y.M. and Elhag, T.M.S. (2007) A Goal Programming Method for Obtaining Interval Weights from an Interval Comparison Matrix. European Journal of Operational Research, 177, 458-471.
http://dx.doi.org/10.1016/j.ejor.2005.10.066 - 4. Wang, Y.M. and Chin, K.S. (2008) A Linear Goal Programming Priority Method for Fuzzy Analytic Hierarchy Process and Its Applications in New Product Screening. International Journal of Approximate Reasoning, 49, 451-465.
http://dx.doi.org/10.1016/j.ijar.2008.04.004 - 5. Sugihara, K., Ishii, H. and Tanaka, H. (2004) Interval Priorities in AHP by Interval Regression Analysis. European Journal of Operational Research, 158, 745-754.
http://dx.doi.org/10.1016/S0377-2217(03)00418-1 - 6. Wang, Y.-M., Luo, Y. and Hua, Z. (2008) On the Extent Analysis Method for Fuzzy AHP and Its Applications. European Journal of Operational Research, 186, 735-747.
http://dx.doi.org/10.1016/j.ejor.2007.01.050 - 7. Wang, Y.M., Yang, J.B. and Xu, D.L. (2005) A Two-Stage Logarithmic Goal Programming Method for Generating Weights from Interval Comparison Matrices. Fuzzy Sets and Systems, 152, 475-498.
http://dx.doi.org/10.1016/j.fss.2004.10.020 - 8. Chandran, B., Golden, B. and Wasil, E. (2005) Linear Programming Models for Estimating Weights in the Analytic Hierarchy Process. Computers & Operations Research, 32, 2235-2254.
http://dx.doi.org/10.1016/j.cor.2004.02.010 - 9. Chang, D.Y. (1996) Applications of the Extent Analysis Method on Fuzzy AHP. European Journal of Operational Research, 95, 649-655.
http://dx.doi.org/10.1016/0377-2217(95)00300-2 - 10. Saaty, T.L. and Vargas, L.G. (2006) Decision Making with the Analytic Network Process: Economic, Political, Social and Technological Applications with Benefits, Opportunities, Costs and Risks. Springer, New York.
- 11. Pankratova, N.D. and Nedashkovskaya, N.I. (2016) Estimation of Consistency of Fuzzy Pairwise Comparison Matrices Using a Defuzzification Method. In: Zgurovsky, M.Z. and Sadovnihiy, V.A., Eds., Springer, 161-172.
- 12. Nedashkovskaya, N.I. (2013) Method of Consistent Pairwise Comparisons When Estimating Decision Alternatives in Terms of Qualitative Criterion. System Research and Information Technologies, 4, 67-79. (In Ukrainian)
http://journal.iasa.kpi.ua/article/view/33943 - 13. Pankratova, N. and Nedashkovskaya, N. (2015) Methods of Evaluation and Improvement of Consistency of Expert Pairwise Comparison Judgements. International Journal of Information Theories and Applications, 22, 203-223.
http://www.foibg.com/ijita/vol22/ijita22-03-p01.pdf - 14. Nedashkovskaya, N.I. (2015) The М_Outflow Method for Finding the Most Inconsistent Elements of a Pairwise Comparison Matrix. System Analysis and Information Technologies: Materials of International Scientific and Technical Conference SAIT, Kyiv, 22-25 June 2015, 95. (In Russian)
http://sait.kpi.ua/books/ - 15. Pankratova, N.D. and Nedashkovskaya, N.I. (2013) The Method of Estimating the Consistency of Paired Comparisons. International Journal of Information Technologies and Knowledge, 7, 347-361.
http://www.foibg.com/ijitk/ijitk-vol07/ijitk07-04-p05.pdf - 16. Chen, S.J. and Hwang, C.L. (1992) Fuzzy Multiple Attribute Decision Making: Methods and Applications. Springer, New York.
http://dx.doi.org/10.1007/978-3-642-46768-4 - 17. Ishibuchi, H. and Tanaka, H. (1990) Multiobjective Programming in Optimization of the Interval Objective Function. European Journal of Operational Research, 48, 219-225.
http://dx.doi.org/10.1016/0377-2217(90)90375-L - 18. Sengupta, A. and Pal, T.K. (2000) On Comparing Interval Numbers. European Journal of Operational Research, 127, 28-43.
http://dx.doi.org/10.1016/S0377-2217(99)00319-7 - 19. Xu, Z.S. and Da, Q.L. (2002) The Uncertain OWA Operator. International Journal of Intelligent Systems, 17, 569-575.
http://dx.doi.org/10.1002/int.10038 - 20. Xu, Z. and Chen, J. (2008) Some Models for Deriving the Priority Weights from Interval Fuzzy Preference Relations. European Journal of Operational Research, 184, 266-280.
http://dx.doi.org/10.1016/j.ejor.2006.11.011 - 21. Wang, Z.-J. and Li, K.W. (2012) Goal Programming Approaches to Deriving Interval Weights Based on Interval Fuzzy Preference Relations. Information Sciences, 193, 180-198.
http://dx.doi.org/10.1016/j.ins.2012.01.019 - 22. Wang, Y.-M. and Elhag, T.M.S. (2006) On the Normalization of Interval and Fuzzy Weights. Fuzzy Sets and Systems, 157, 2456-2471.
http://dx.doi.org/10.1016/j.fss.2006.06.008 - 23. Nedashkovskaya, N. (2015) Pairwise Comparison Models on the Basis of Interval Expert Judgments. Questions of Applied Mathematics and Mathematical Modeling, 15, 121-137. (In Russian)









