Intelligent Control and Automation
Vol.5 No.1(2014), Article ID:43067,5 pages DOI:10.4236/ica.2014.51003
General Integral Control Design via Feedback Linearization
Academe of Naval Submarine, Qingdao, China
Email: baishunliu@163.com, jianhui_li@163.com, qdqtlxq@sina.com
Copyright © 2014 Baishun Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Baishun Liu et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received July 10, 2013; revised August 10, 2013; accepted August 17, 2014
KEYWORDS
General Integral Control; Nonlinear Control; Robust Control; Nonlinear Integrator; Feedback Linearization; Output Regulation
ABSTRACT
Based on the feedback linearization technique, we present a systematic design method for the General Integral Control and a new integral control strategy along with a class of fire-new integrator. By using the linear system theory and Lyapunov method along with LaSalle’s invariance principle, the conditions on the control gains to ensure regionally as well as semi-globally asymptotic stability are provided. Theoretical analysis and simulation results demonstrated that: by using this design method, General Integral Control can deal with nonlinearity and uncertainties of dynamics more effectively; the optimum response can be achieved in the whole control domain, even under uncertain payload and varying-time disturbances. This means that General Integral Control has strong robustness, fast convergence, good flexibility, and then makes the engineers design a high performance controller more easily.
1. Introduction
Integral control [1] plays an important role in control system design because it ensures asymptotic tracking and disturbance rejection. In the presence of the parametric uncertainties and unknown constant disturbances, integral control can still preserve the stability of the closedloop system and create an equilibrium point at which the tracking error is zero. The main task of the integral controller is to stabilize this point, which is challenging because it depends on uncertain parameters and unknown disturbances.
The design of integral control for general linear systems was done in the 1970’s in the work of Davision, Francis, and others [2,3]. In the early 1990’s, Isidori and Byrnes [4] extended integral control to nonlinear systems. Their results, however, were local. Regional and semiglobal results for integral control appeared later in the work of Khalil [1,5]. These papers dealt with minimumphase input-output linearizable systems and designed output feedback control using high-gain observers and the tool of saturating the control outside a compact region of interest. All these design methods above for integral control are achieved by using a conventional integrator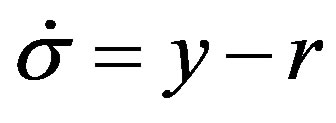 , where
, where 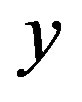 is the controlled output and
is the controlled output and 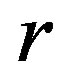 is a constant reference. In 2009, we originated General Integral Control in [6], which presented a unified framework for General Integral Control, some general integrator, and the necessary conditions and basic principles for designing a general integrator. Based on linear system theory, we presented a systematic design method for General Integral Control [7] with a linear integrator in 2012. The results, however, were local. In 2012, regional and semi-global results were proposed in [8], which presented a nonlinear integrator shaped by sliding mode manifold. And then, General Integral Control design was achieved by sliding mode technique and linear system theory.
is a constant reference. In 2009, we originated General Integral Control in [6], which presented a unified framework for General Integral Control, some general integrator, and the necessary conditions and basic principles for designing a general integrator. Based on linear system theory, we presented a systematic design method for General Integral Control [7] with a linear integrator in 2012. The results, however, were local. In 2012, regional and semi-global results were proposed in [8], which presented a nonlinear integrator shaped by sliding mode manifold. And then, General Integral Control design was achieved by sliding mode technique and linear system theory.
In this paper, based on feedback linearization technique, we present a systematic design method for General Integral Control. The main contributions are as follows: 1) A new integral control strategy along with a class of firenew integrator is proposed; 2) By using linear system theory and Lyapunov method along with LaSalle’s invariance principle, the conditions on the control gains to ensure regionally as well as semi-globally asymptotic stability are provided.
Throughout this paper, we use the notation  and
and  to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix
to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix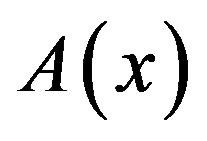 , for any
, for any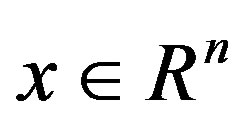 . The norm of vector
. The norm of vector 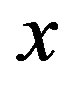 is defined as
is defined as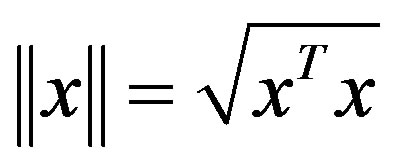 , and that of matrix
, and that of matrix
 is defined as the corresponding induced norm
is defined as the corresponding induced norm
 .
.
The remainder of the paper is organized as follows. Section 2 describes the system under consideration, assumptions, and General Integral Control law proposed here. Section 3 addresses the systematic design method of General Integral Control. Example and simulation are provided in Sections 4. Conclusions are presented in Section 5.
2. Problem Formulation
Consider the feedback linearizable system,
 (1)
(1)
where  is the state,
is the state, 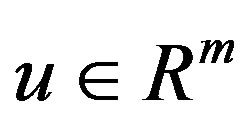 is the control input,
is the control input, 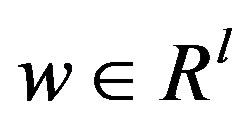 is a vector of unknown constant parameters and disturbances. The function
is a vector of unknown constant parameters and disturbances. The function  and
and 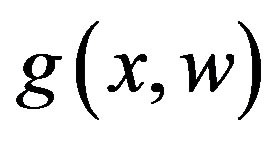 are continuous in
are continuous in  on a domain,
on a domain,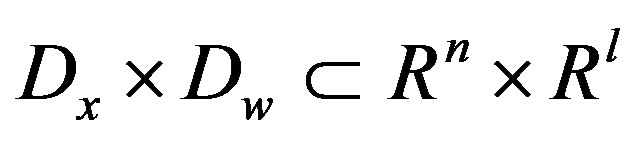 . The inequality,
. The inequality,  holds for all
holds for all 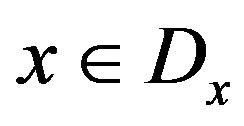 and
and .
.
Assumption 1: Suppose that there is a unique pair 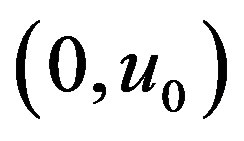 that satisfies the equation,
that satisfies the equation,
 (2)
(2)
so that  is the steady-state control that is needed to maintain equilibrium at the origin.
is the steady-state control that is needed to maintain equilibrium at the origin.
Assumption 2: Suppose that there is a diffeomorphism
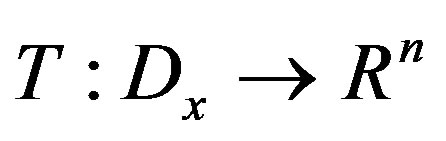 such that
such that 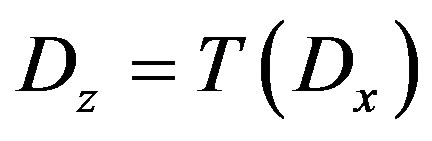 contains the origin and
contains the origin and  satisfies the partial differential equations,
satisfies the partial differential equations,
 (3)
(3)
where  is controllable,
is controllable, 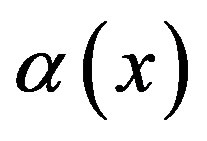 and
and  are all known nonlinear functions,
are all known nonlinear functions, 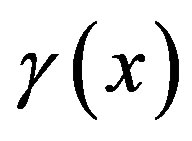 is nonsingular for all
is nonsingular for all
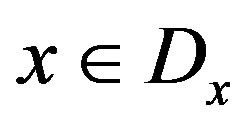 ,
,  and
and 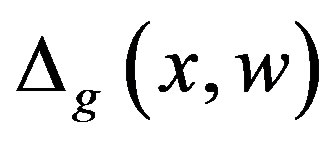 are the uncertain terms of the system (1), which arises from several practical reasons such as model simplification, parameter uncertainty, computational errors.
are the uncertain terms of the system (1), which arises from several practical reasons such as model simplification, parameter uncertainty, computational errors.
The change of variables 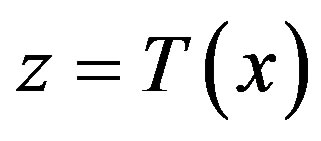 transforms the system (1) into the form,
transforms the system (1) into the form,
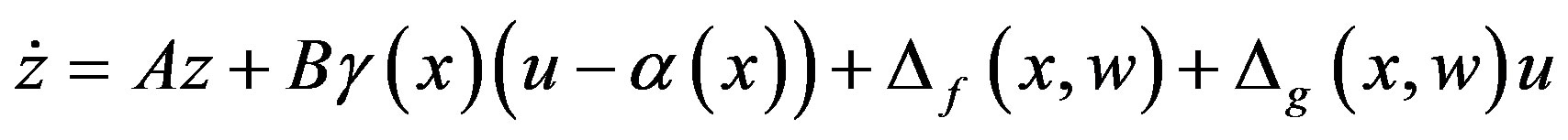 (4)
(4)
For stabilizing the system (4), we need to include “integral action” in the control law . Therefore, General Integral Controller is proposed as follows,
. Therefore, General Integral Controller is proposed as follows,
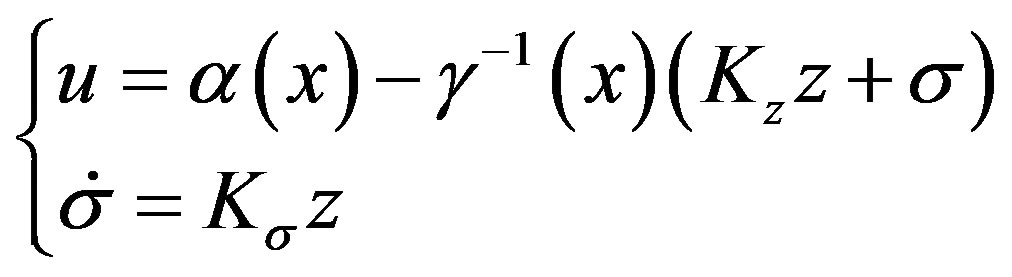 (5)
(5)
where  and
and  are all positive define matrices.
are all positive define matrices.
Thus, substituting (5) into (4) to obtain the augmented system,
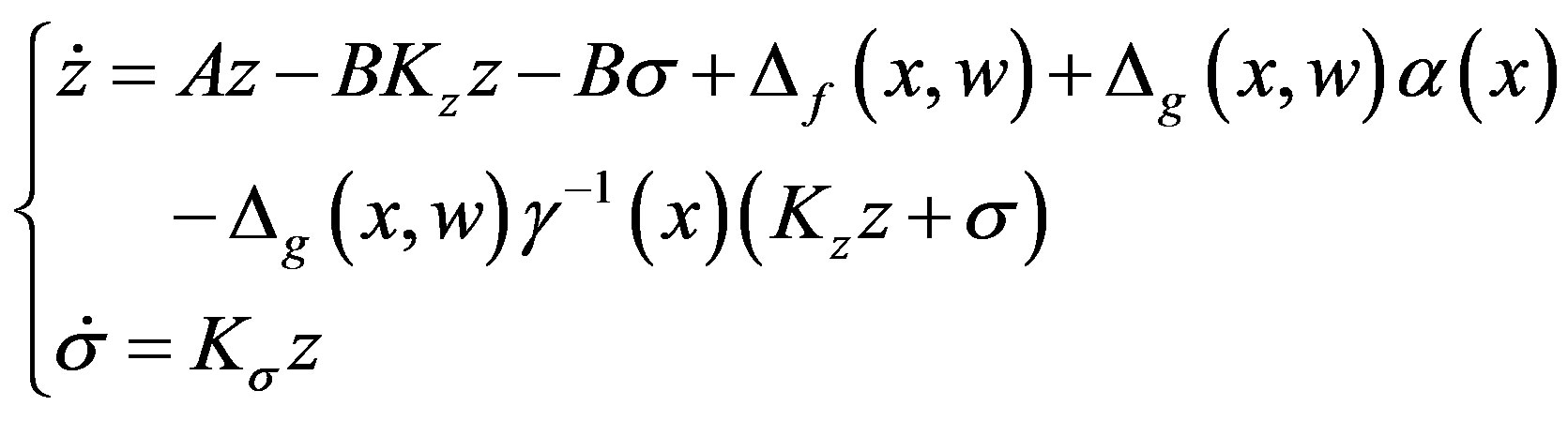 (6)
(6)
By setting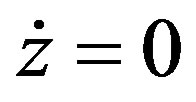 ,
, 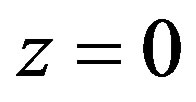 and
and  in (6), we obtain,
in (6), we obtain,
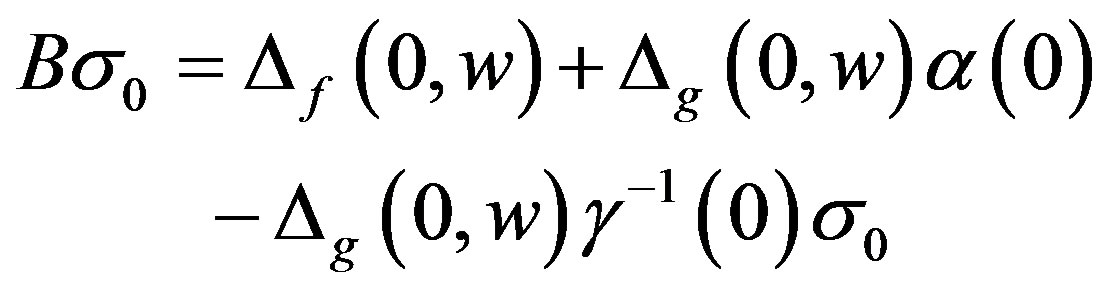 (7)
(7)
By Assumption 1 and choosing 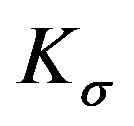 nonsingular to counteract the constant uncertainties, we ensure that there is a unique solution,
nonsingular to counteract the constant uncertainties, we ensure that there is a unique solution, 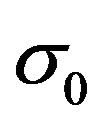 , and then
, and then  is a unique equilibrium point of the closed-loop system (6) in a domain of interest. At the equilibrium point,
is a unique equilibrium point of the closed-loop system (6) in a domain of interest. At the equilibrium point,  , irrespective of the value of
, irrespective of the value of .
.
Remark 1: From the control law (5), it is not hard to see that the integrator to be shaped by diffeomorphism  is a fire new integrator. And then, it resulted in a class of fire-new general integral controller and design method.
is a fire new integrator. And then, it resulted in a class of fire-new general integral controller and design method.
Now, the design task is to provide the conditions on the gain matrices  and
and 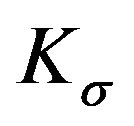 such that
such that 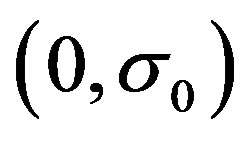 is an asymptotically stable equilibrium point of the closedloop system (6) in the control domain of interest, which is not a trivial task because the closed-loop system (6) depends on the unknown vector
is an asymptotically stable equilibrium point of the closedloop system (6) in the control domain of interest, which is not a trivial task because the closed-loop system (6) depends on the unknown vector , the uncertain terms
, the uncertain terms
 and
and . In the next section, we will propose a systematic design method to this dilemma.
. In the next section, we will propose a systematic design method to this dilemma.
3. Design Method
For analyzing the stability of the closed-loop system (6), we substitute (7) into (6) and obtain,
 (8)
(8)
where

For stabilizing the system (8), we need to know some bound information on . This results in the following assumptions.
. This results in the following assumptions.
Assumption 3: By Assumption 2 and the function
 and
and 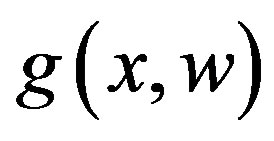 are continuous in
are continuous in  on a domain,
on a domain, 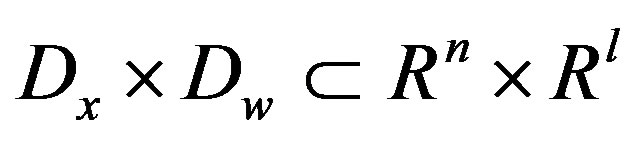 and
and , it is reasonable to suppose that the following inequalities hold,
, it is reasonable to suppose that the following inequalities hold,
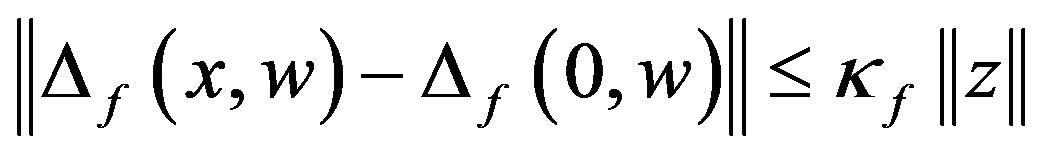 (9)
(9)
 (10)
(10)
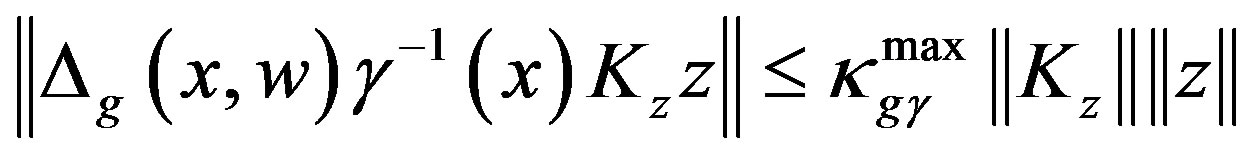 (11)
(11)
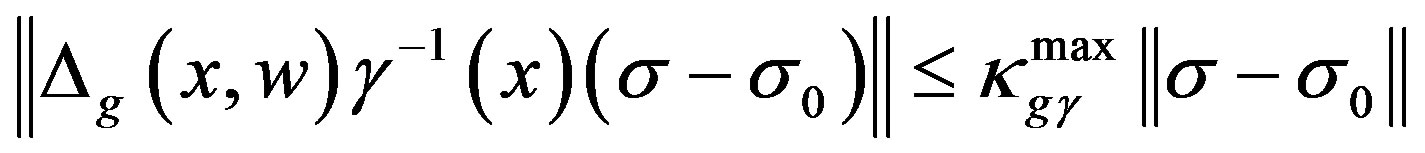 (12)
(12)
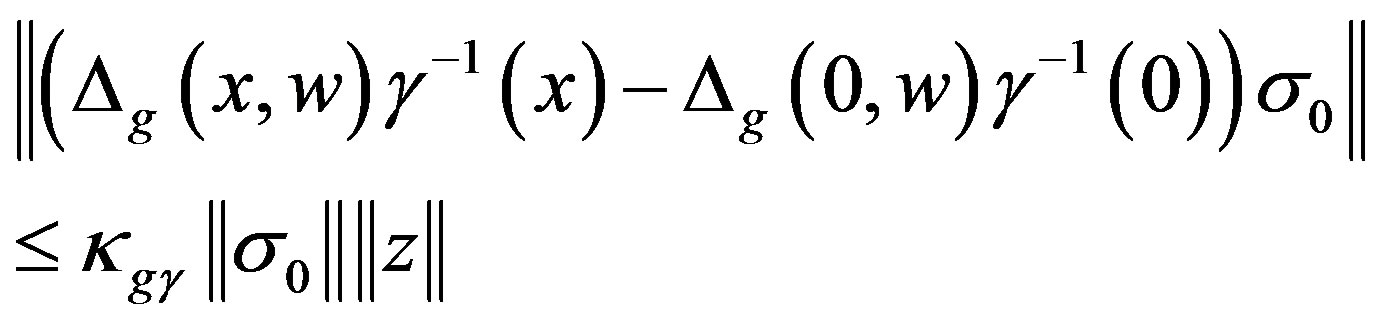 (13)
(13)
Thus, by the definition of  and (9)~(13)we obtain,
and (9)~(13)we obtain,
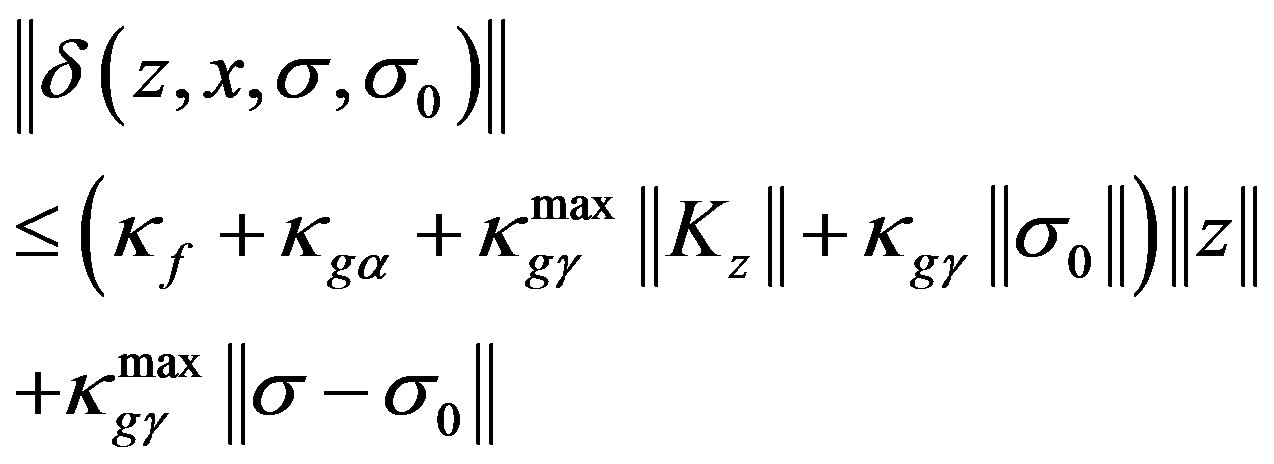 (14)
(14)
where ,
,  ,
,  , and
, and  are all positive constants.
are all positive constants.
Setting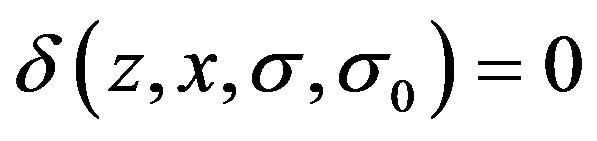 , the equation (8) can be rewritten as,
, the equation (8) can be rewritten as,
 (15)
(15)
where
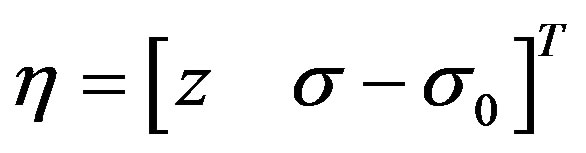 and
and 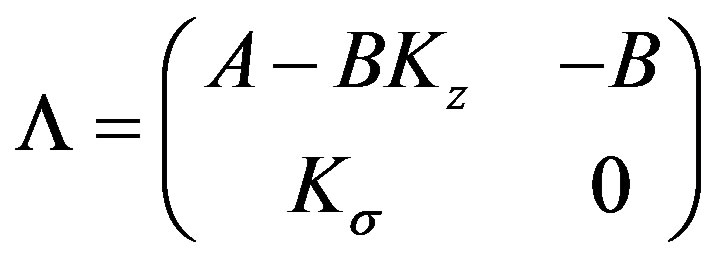
Based on linear system theory [5], we can choose 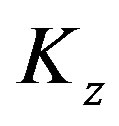 and
and 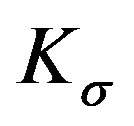 such that
such that  is Hurwitz, and then for any given positive define symmetric matrix
is Hurwitz, and then for any given positive define symmetric matrix 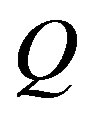 there exists a unique positive define symmetric matrix
there exists a unique positive define symmetric matrix  that satisfied Lyapunov equation (16). Consequently, there exists a quadratic Lyapunov function,
that satisfied Lyapunov equation (16). Consequently, there exists a quadratic Lyapunov function, .
.
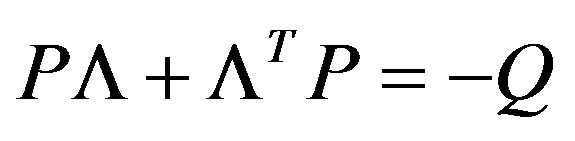 (16)
(16)
We use  as a Lyapunov function candidate. Obviously,
as a Lyapunov function candidate. Obviously, 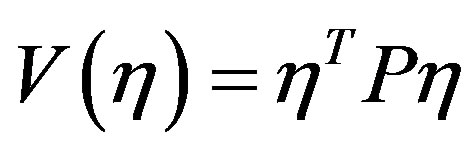 is positive define.
is positive define.
Therefore, our task is to show that its time derivative along the trajectories of the closed-loop system (8) is negative define, which is given by,
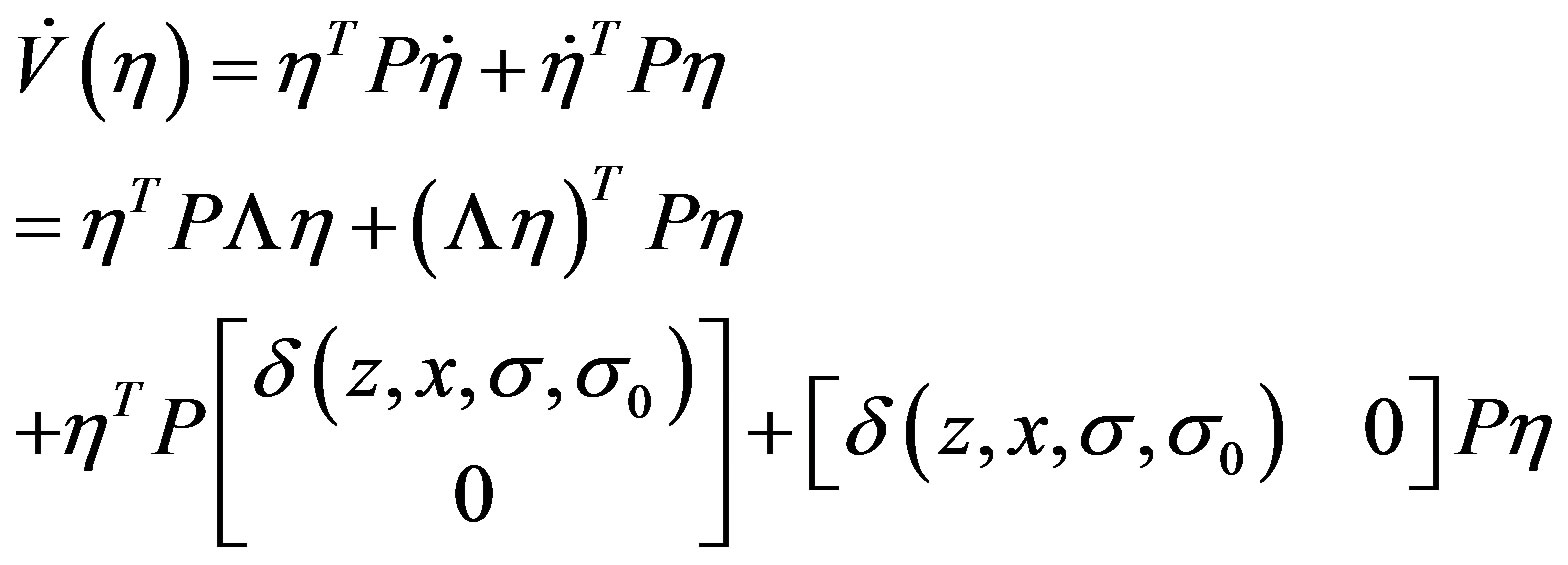 (17)
(17)
Now, by definition of , we have
, we have  and
and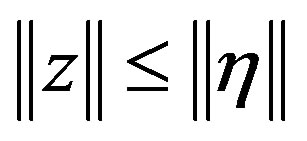 , and then inequality (14) can be rewritten as,
, and then inequality (14) can be rewritten as,
 (18)
(18)
where .
.
Substituting (18) into (17) and taking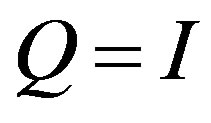 , we obtain,
, we obtain,
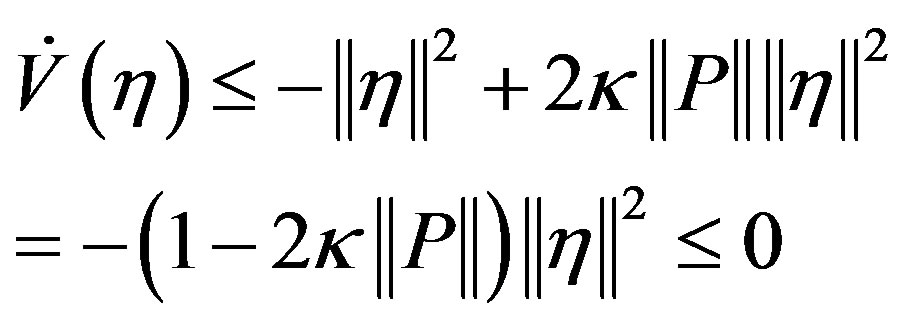 (19)
(19)
Using the fact that Lyapunov function 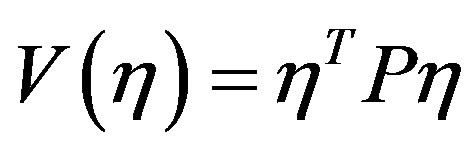
is a positive define function and its time derivative is a negative define function if the inequality (19) holds, we conclude that the closed-loop system (8) is stable. In fact,
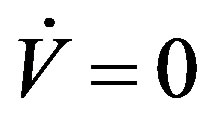 means
means 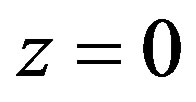 and
and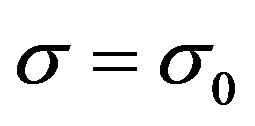 . By invoking the LaSalle’s invariance principle [5], it is easy to know that the closed-loop system (8) is asymptotically stable in the control domain of interest. This established the following theorem.
. By invoking the LaSalle’s invariance principle [5], it is easy to know that the closed-loop system (8) is asymptotically stable in the control domain of interest. This established the following theorem.
Theorem 1: Let  be a unique equilibrium point for the closed-loop system (8). If Assumptions 1 ~ 3 hold and there exist the gain matrices
be a unique equilibrium point for the closed-loop system (8). If Assumptions 1 ~ 3 hold and there exist the gain matrices 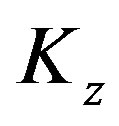 and
and  such that the inequality (19) holds, and then the closedloop system (8) is asymptotically stable in the domain
such that the inequality (19) holds, and then the closedloop system (8) is asymptotically stable in the domain
 . Moreover, if all assumptions hold globally, and then it is globally asymptotically stable.
. Moreover, if all assumptions hold globally, and then it is globally asymptotically stable.
Remark 2: From the analysis procedure above, it is obvious that the distinct feature of this design method is:
1) Just the integrator is taken as, 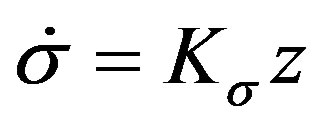 , we can easily use linear system theory to analyze the stability of the closed-loop system; 2) Just the integral control action is introduced, we can use the linear growth bound to estimate the impact of the uncertain term,
, we can easily use linear system theory to analyze the stability of the closed-loop system; 2) Just the integral control action is introduced, we can use the linear growth bound to estimate the impact of the uncertain term, 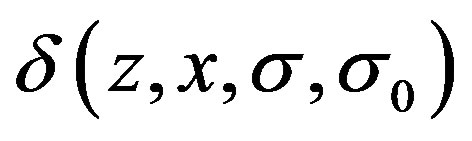 on the system stability. All of them provide an ingenious solution for designing a stable general integral controller.
on the system stability. All of them provide an ingenious solution for designing a stable general integral controller.
Discussion 1: Compared with General Integral Control design proposed by [7,8], it is easy to see that: 1) The design method proposed here can cancel the central nonlinear action via feedback linearization; 2) When the bound of the system uncertainty is fairly estimated we can design a stable general integral controller with the lesser conservativeness. All those mean that general integral control design method proposed here can more effectively deal with nonlinearity and uncertainty of dynamics, and then makes the engineers more easily design a stable controller.
4. Example and Simulation
Consider the pendulum system [5] described by,
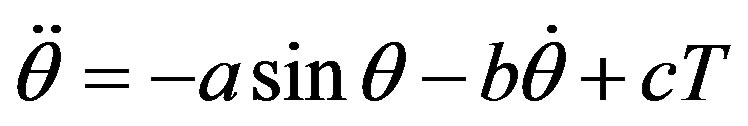
where ,
,  ,
, 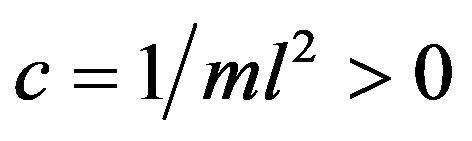 ,
,  is the angle subtended by the rod and the vertical axis, and
is the angle subtended by the rod and the vertical axis, and 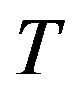 is the torque applied to the pendulum. View
is the torque applied to the pendulum. View 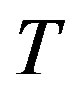 as the control input and suppose we want to regulate
as the control input and suppose we want to regulate  to
to
 . Taking
. Taking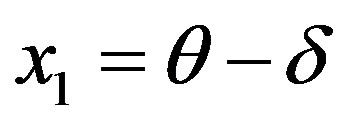 ,
,  , we can write the pendulum system as,
, we can write the pendulum system as,
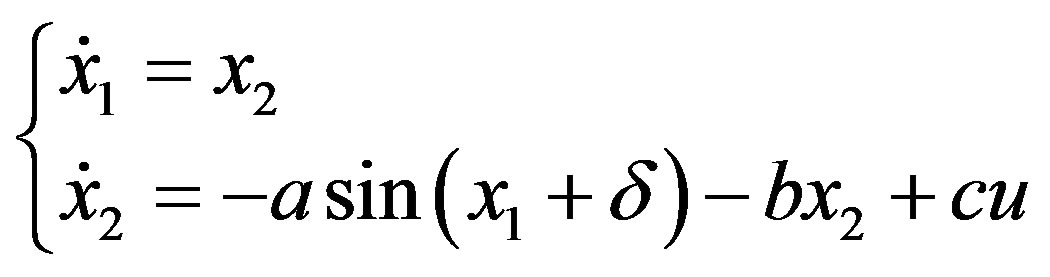 (20)
(20)
It can be easily seen that the system (20) is feedback linearizable with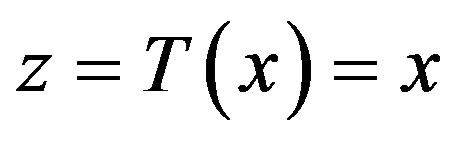 . Thus, general integral controller can be taken as,
. Thus, general integral controller can be taken as,
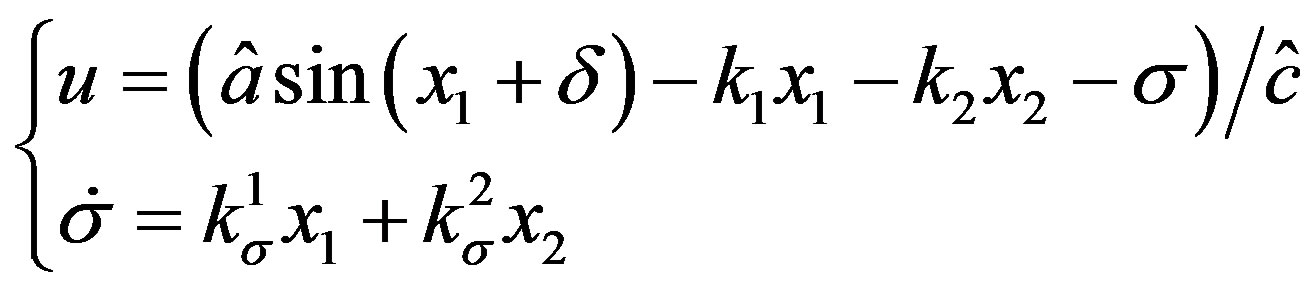 (21)
(21)
where 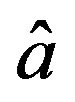 and
and  are the nominal values of
are the nominal values of  and
and .
.
Substituting (21) into (20), we obtain,
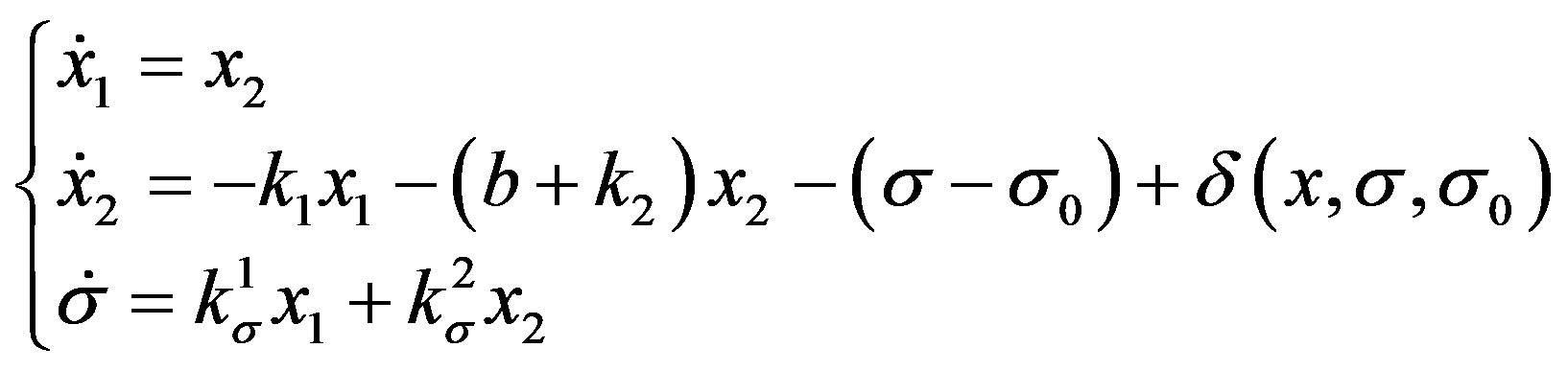 (22)
(22)
where
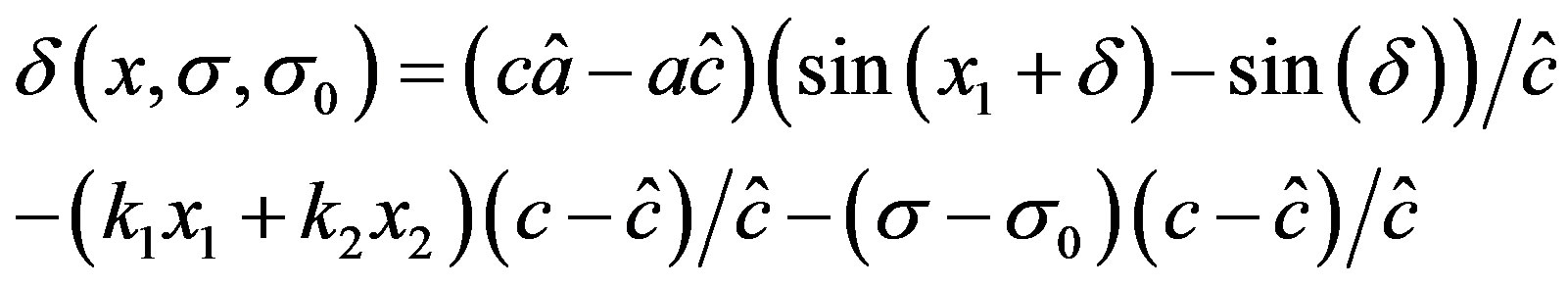 .
.
For the closed-loop system (22), taking 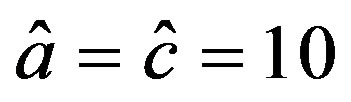 as the nominal values of
as the nominal values of  and
and , and using the design method proposed here, general integral controller can be taken as,
, and using the design method proposed here, general integral controller can be taken as,
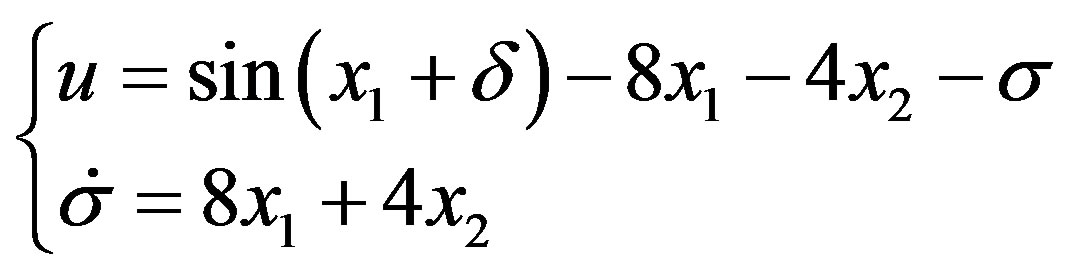
Thus, regulation will be achieved for all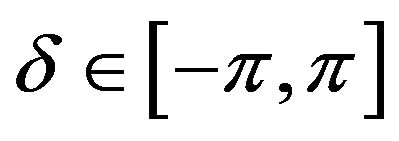 .
.
In simulation, the normal parameters are 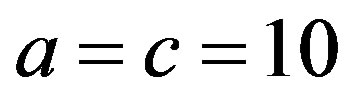 and
and . In the perturbed case,
. In the perturbed case, 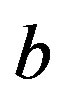 and
and  are reduced
are reduced

Figure 1. System output under normal (solid line) and perturbed case (dashed line).
to 0.5 and 5, respectively, corresponding to doubling of the mass. Moreover, we consider an additive impulselike disturbance 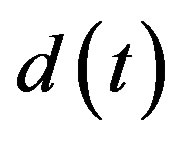 of magnitude 30 acting on the system input between 11 s and 12 s.
of magnitude 30 acting on the system input between 11 s and 12 s.
Figure 1 showed the simulation results under normal (solid line) and perturbed (dashed line) cases. The following observations can be made: under normal and perturbed cases, the optimum response in the whole domain of interest can all be achieved by a set of the same control gains, even under the case that the payload is changed abruptly. This demonstrates that general integral control proposed here has strong robustness, fast convergence and good flexibility, and then can more effectively deal with unknown exogenous disturbances, nonlinearity and uncertainties of dynamics and makes the engineers more easily design a high performance controller.
5. Conclusions
Based on the feedback linearization technique, we present a systematic design method for General Integral Control. The main contributions are as follows: 1) A new integral control strategy along with a class of fire-new integrator is proposed; 2) By using the linear system theory and Lyapunov method along with LaSalle’s invariance principle, the conditions on the control gains to ensure regionally as well as semi-globally asymptotic stability are provided.
In this paper, only one design method for General Integral Control was presented. It is clear that we cannot expect one particular procedure to apply to all system. Therefore, new design techniques for General Integral Control are needed to solve wider theoretical and practical problems.
REFERENCES
- H. K. Khalil, “Universal Integral Controllers for Minimum-Phase Nonlinear Systems,” IEEE Transactions on Automatic Control, Vol. 45, No. 3, 2000, pp. 490-494. http://dx.doi.org/10.1109/9.847730
- E. J. Davison, “The Robust Control of A Servomechanism Problem for Linear Time-Invariant Multivariable Systems,” IEEE Transactions on Automatic Control, Vol. 21, No. 1, 1976, pp. 25-34. http://dx.doi.org/10.1109/TAC.1976.1101137
- B. A. Francis, “The Linear Multivariable Regulator Problem,” SIAM Journal on Control and Optimization, Vol.15, No. 3, 1977, pp. 486-505. http://dx.doi.org/10.1137/0315033
- A. Isidori and C. I. Byrnes, “Output Regulation of Nonlinear Systems,” IEEE Transactions on Automatic Control, Vol. 35, No. 2, 1990, pp. 131-140. http://dx.doi.org/10.1109/9.45168
- H. K. Khalil, “Nonlinear Systems,” Electronics Industry Publishing, Beijing, 2007.
- B. S. Liu and B. L. Tian, “General Integral Control,” Proceedings of the International Conference on Advanced Computer Control, Singapore City, 22-24 January 2009, pp. 136-143. http://dx.doi.org/10.1109/ICACC.2009.30
- B. S. Liu, and B. L. Tian, “General Integral Control Design Based on Linear System Theory,” Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, Baotou, Vol. 5, 2012, pp. 3174- 3177.
- B. S. Liu and B. L. Tian, “General Integral Control Design Based on Sliding Mode Technique,” Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, Baotou, Vol. 5, 2012, pp. 3178-3181.

