Intelligent Control and Automation
Vol.4 No.2(2013), Article ID:31733,12 pages DOI:10.4236/ica.2013.42018
Particle Swarm Optimization (PSO) Based Turbine Control
1Faculty of Engineering and Applied Science, University of Ontario Institute of Technology, Oshawa, Canada
2Faculty of Energy Systems and Nuclear Science, University of Ontario Institute of Technology, Oshawa, Canada
Email: *hossam.gaber@uoit.ca
Copyright © 2013 Ali Tarique, Hossam A. Gabbar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 22, 2012; revised March 14, 2013; accepted March 21, 2013
Keywords: PSO; PID Controller; GA; Optimization
ABSTRACT
The steam turbine control system is strongly non-linear in all operating conditions. Proportional-Integral-Derivative (PID) controller that is currently used in control systems of many types of equipment is not considered highly precision for turbine speed control system. A fine tuning of the PID controller by some optimization technique is a desired objective to maintain the precise speed of the turbine in a wide range of operating conditions. This Paper evaluates the feasibility of the use of Particle Swarm Optimization (PSO) method for determining the optimal Proportional-Integral-Derivative (PID) controller parameters for steam turbine control. The turbine speed control is modelled in SimulinkTM with PID controller and the PSO algorithm is implemented in MATLAB to optimize the PID function. The PSO optimization technique is also compared with Genetic Algorithm (GA) and it is validated that PSO based controller is more efficient in reducing the steady-states error; settling time, rise time, and overshoot limit in speed control of the steam turbine control.
1. Introduction
A steam turbine is a machine that converts thermal energy of pressurized steam to mechanical energy in the form of rotary motion. From traditional fossil fuel based power plant to nuclear power plant steam turbine is a widely used prime mover. It normally operates at 3600 rpm speed while in the nuclear industry it runs at 1800 rpm speed. The control of the turbine is indispensable, as turbines need to be run up slowly, to prevent damage as well as require precise speed control to follow the generator load variation. The control system and protection are separate although they have the same system with Controller/Governor, actuator with arm and series valves. The speed throughout the operation of the system needs to be controlled by the governor. The governor gets input signals from the generator, theturbine shaft, thesteam main output (input for turbine) pressure and thesteam outlet/extraction pressure of the turbine.
PID control was an essential element of a governor and it became the standard tool when process controls emerge in the 1940s. Today in the process control system, the usage of PID type control loops exceeded 95% [1]. PID controlsystem is designed to control the main steamflow to the steam turbine in all operational conditions by means of the control equipment comprising of a governor, turbine throttle, admission, and or extraction control valves. Optimal performance of these components throughout the steam turbines operational life improves the life cycle of the system as well as the cost efficiency. Optimal performance in another way is even more important than before as previous turbines operate beyond their original life expectancy. After the development of digital processing technology turbine control systems are also replaced with digital controls achieving faster processing speed, lower cost and compactness. However, there exist some variables in continuous distributed control system (DCS) that experiences many unpredicted disturbance during operation. A PID control system is then combined with logic, sequential functions, selectors, and simple function blocks to build up a more efficient automation system that are used inenergy, transportation, and manufacturing sectors [2].
Steam turbine governing system is a nonlinear system whatsoever it is used in the mechanical governor or in the modern digital control governor. PID being one of the widely used controllers is in use for steam turbine governing since its development. The control strategy of the steam turbine governing system stays mainly at the control with PID, but additionally with the tuning of the PID components. One of the early methods of controller tuning is the Fuzzy logic method. But Fuzzy control doesn't necessary need the accurate mathematical model of the object, which fit to the nonlinear system. Intelligent integration fuzzy of control is adopted and simulation was done with PID controller. The simulation results enunciate that the performance of steam turbine governing system with intelligent integration fuzzy control is better than which with conventional PID control, carrying advantages such as small super-adjusting, high-speed response, short transition process time and no steadystate error and so on [3]. Optimization with a direct search method was thought a more effective in NelderMead’s method [4]. However, application of NelderMead’s method for the optimization of the automatic control systems with the fuzzy regulators does not result a precision optimum decision. A global optimization of the search space is required as stated by Sabanin et al. [5]. Golberg in his research depicted that optimization with Genetic Algorithm is a favoured method in complex control parameters [6]. Strategy of search of optimum solution in Genetic algorithms is based on hypothesis that the more fitness of an individual is higher with the higher probability that descendants got with its involvement [7]. Genetic algorithm is a stochastic optimization technique that is originally based on the theory of natural selection and evolutionary genetics. Lin et al. in their research has introduced GA technique to tune the gains of PID control for brushless DC motor [8]. GA technique has widely used to solve complex optimization problems; however recent research has identified some deficiencies in GA performance [9]. The crossover and mutation; the two main operations of GA cannot guarantee better fitness of offspring as the chromosomes in the population have similar structure and their average fitness are high toward the end of the evolutionary process [10]. Kennedy and Eberhart developed one of the modern heuristic algorithms known as PSO that has been stirred by the behavior of organisms, such as fish schooling and bird flocking [11]. Members of fish schooling or bird flocking follows an inherent rules to undertake a synchronized movement so that they don’t collide. This phenomenon is used to optimize the complex solutions using PSO. PSO is characterized as easy to execute, and computationally proficient heuristic technique. This algorithm in comparison to GA has a faster speed and faster premature convergence [12]. It also has a flexible and well-balanced mechanism to improve the exploration abilities [13]. In PSO, the particles are updated according to their current positions and velocities [14]. The prospective solutions, called particles, fly through the problem space following the current optimum particles [15]. The position of a particle represents a candidate solution to the optimization problem. Each particle within the space changes its velocity and position according to rules originally motivated by behavioral models of bird flocking. Each time it identifies a better fitness value, stores it and represents it as pbest. It continues an iterative process and finally updated two best values; one is pbest and the other one gbest, the global best throughout the population.
2. Proposed Turbine Control Model
As shown in Figure 1, the proposed model consists of a
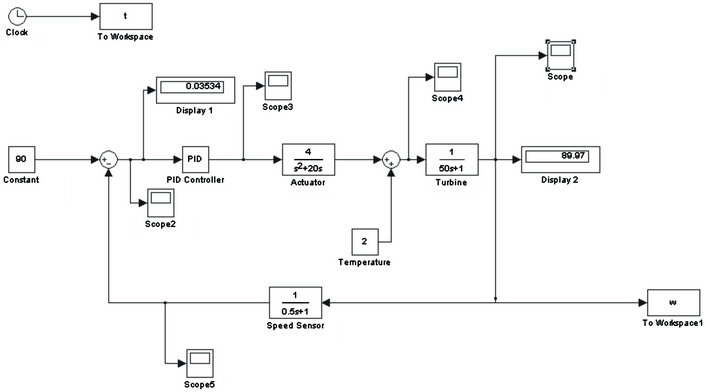
Figure 1. Model of turbine control with PID controller.
controller, actuator, the turbine and the process measuring equipments. In a steady state condition desired input and error value are the input of the controller. The controller compares the desired input and error function and develops a manipulated variable to feed to the actuator. The actuator controls the steam control valve to control the turbine speed. This PID controller is optimized with PSO and GA separately and the results are compiled in next section.
3. Controller Design
The proportional-integral-derivative (PID) controller is utilized in this design and latter tuned using PSO and GA. As shown in the flow diagram in Figure 2, the “error” value 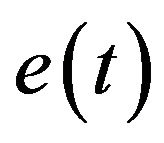 is calculated as the difference between the desired set point
is calculated as the difference between the desired set point 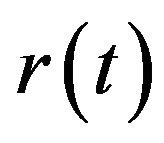 and measured process variable
and measured process variable  at any instant of time
at any instant of time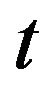 . The controller input
. The controller input 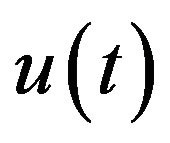 is determined from the Equation (1).
is determined from the Equation (1).
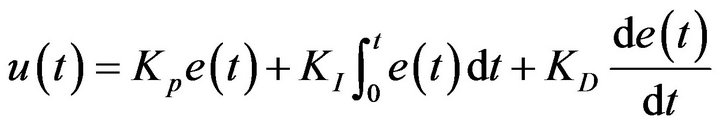 (1)
(1)
In this control algorithm, P corresponds the proportional term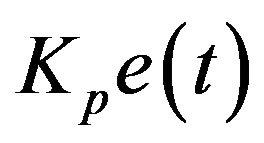 , where
, where  is the proportional gain of the controller. Similarly, I represent the integral term
is the proportional gain of the controller. Similarly, I represent the integral term
 and D stands for the derivative term
and D stands for the derivative term 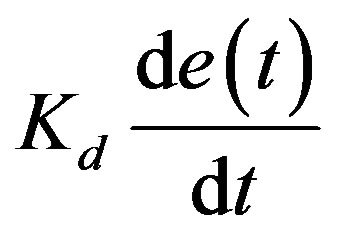 of the controller.
of the controller.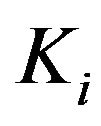 and
and 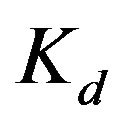 are integral and derivative gain of the controller, respectively. The transfer function of the PID controller is as follows,
are integral and derivative gain of the controller, respectively. The transfer function of the PID controller is as follows,
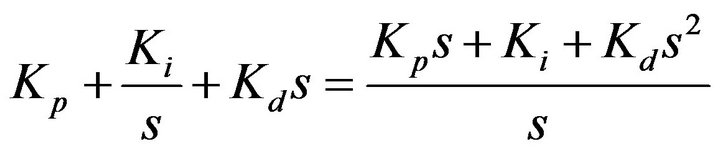 (2)
(2)
Using these three terms, the controller by adjusting the process control input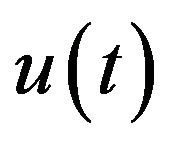 , minimizes the error value. The weighted sum of the three components is used to adjust the process by a control element, as in the steam turbine control a flow control valve.
, minimizes the error value. The weighted sum of the three components is used to adjust the process by a control element, as in the steam turbine control a flow control valve.
4. Design Optimization Tools
In this paper, the PID controller is optimized to achieve the optimal behaviour of the plant. The optimizer is used to search for the optimal solution of the PID control gains
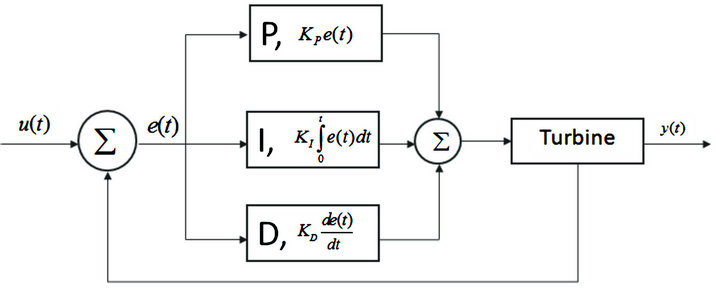
Figure 2. Block diagram of a PID control.
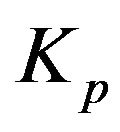 ,
, 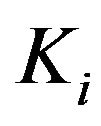 , and
, and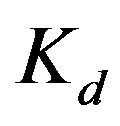 . Intelligent optimization algorithms are appropriate choices in selecting an optimizer. The proposed methodology utilizes Particle Swarm Optimization (PSO) tools. To investigate the effectiveness of utilization of PSO in respect to Genetic Algorithm (GA), the numerous simulations of both the techniques have been performed and the results are compared.
. Intelligent optimization algorithms are appropriate choices in selecting an optimizer. The proposed methodology utilizes Particle Swarm Optimization (PSO) tools. To investigate the effectiveness of utilization of PSO in respect to Genetic Algorithm (GA), the numerous simulations of both the techniques have been performed and the results are compared.
4.1. Genetic Algorithm
Genetic Algorithm (GA) utilizes evolution operations, such as, selection, crossover and mutation. In GA, the design variable  consists of PID control gains, as shown in the following equation.
consists of PID control gains, as shown in the following equation.
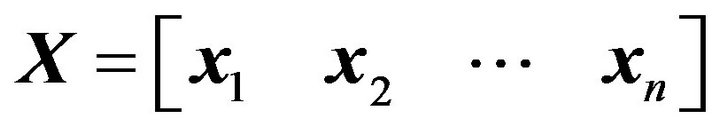 (3)
(3)
and
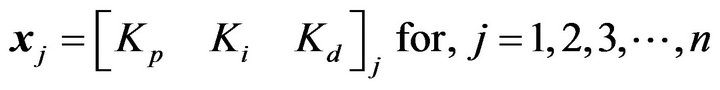 (4)
(4)
A population of 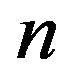 sets of these design variables are send forward to evaluate the objective function
sets of these design variables are send forward to evaluate the objective function 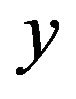 by genetic algorithm (GA).
by genetic algorithm (GA).
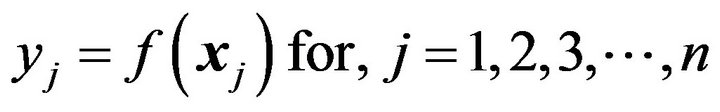 (5)
(5)
After each of the n objective functions are evaluated, the resultant set 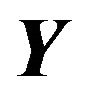 of objective function values are checked whether the convergence criteria are met.
of objective function values are checked whether the convergence criteria are met.
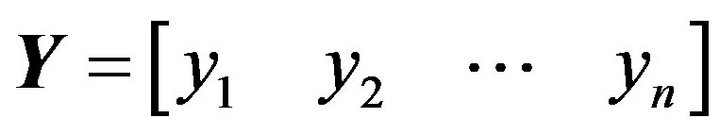 (6)
(6)
If not, the n objective function values are returned back to GA. Based on these values, GA generates next generation of design variable set by performing genetic operations, namely, selection, crossover, and mutation. This process continues until the convergence is reached as shown in Figure 3.
4.2. Particle Swarm Optimization
In PSO, each particle contains these three components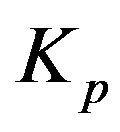 ,
,  , and
, and 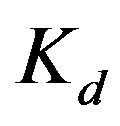 and updates the components in each iteration to find the Pbest and Gbest. Finally, the program runs to converge to the optimal solution. PSO has many similarities with evolutionary computation techniques like Genetic Algorithms (GA). As shown in Figure 4 the system is initialized with a population of random solutions and searches for optima by updating generations. In PSO, the potential solutions, called particles, fly through the problem space by following the current optimum particles.
and updates the components in each iteration to find the Pbest and Gbest. Finally, the program runs to converge to the optimal solution. PSO has many similarities with evolutionary computation techniques like Genetic Algorithms (GA). As shown in Figure 4 the system is initialized with a population of random solutions and searches for optima by updating generations. In PSO, the potential solutions, called particles, fly through the problem space by following the current optimum particles.
It is demonstrated that PSO has advantages over other methods in respect to run time, cost and better result. Another reason that PSO is attractive is that there are few parameters to adjust. One version, with slight variations, works well in a wide variety of applications. Particle
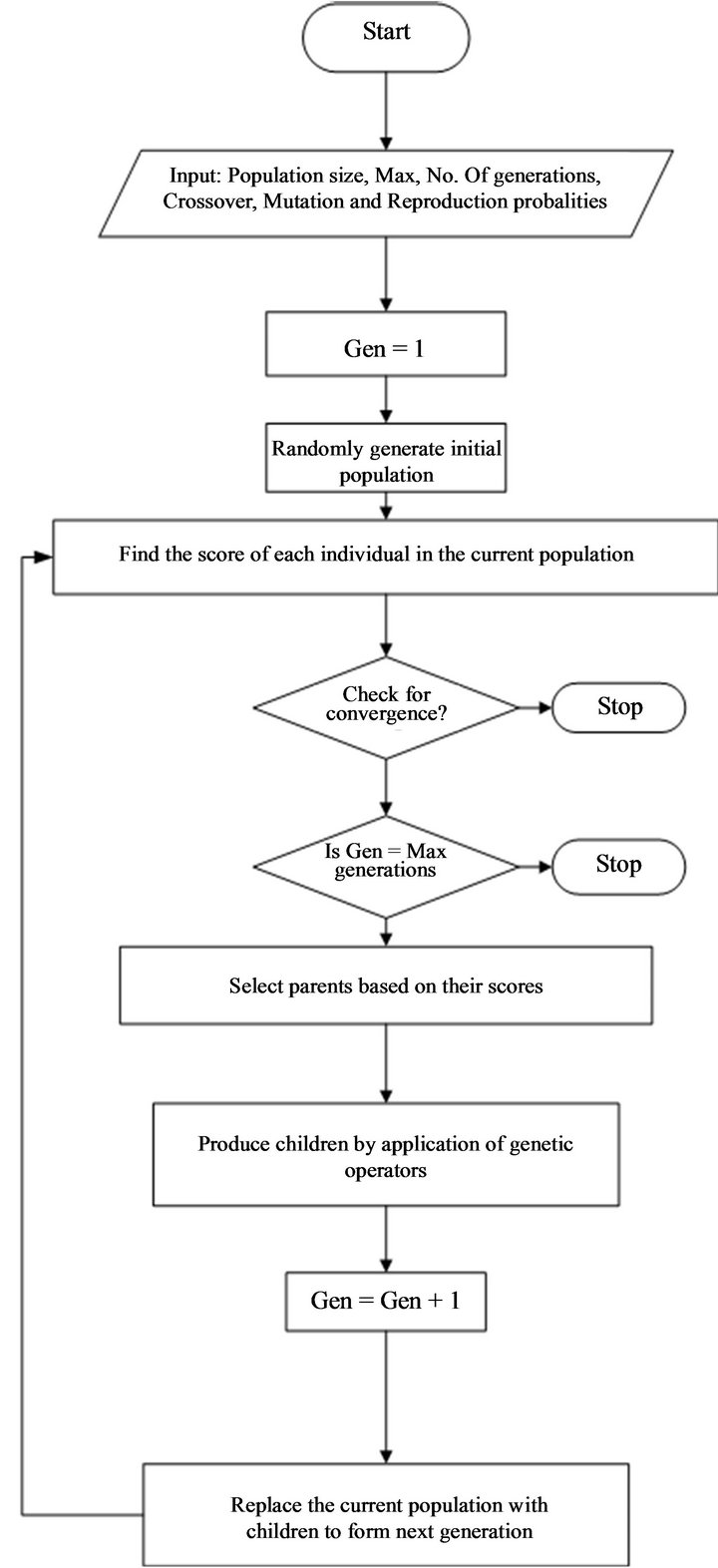
Figure 3. Genetic algorithm used for turbine control optimization.
swarm optimization has been used for approaches that can be applied across a wide range of applications, as well as for specific applications focused on a specific requirement.
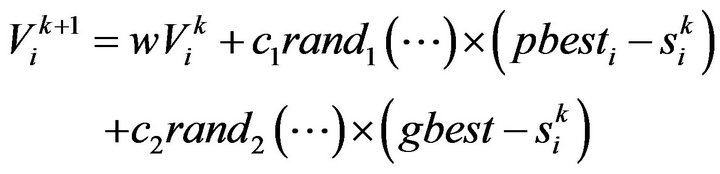 (7)
(7)
where,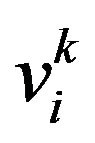 : velocity of agent i at iteration kw: weighting functioncj: weighting factor,
: velocity of agent i at iteration kw: weighting functioncj: weighting factor,
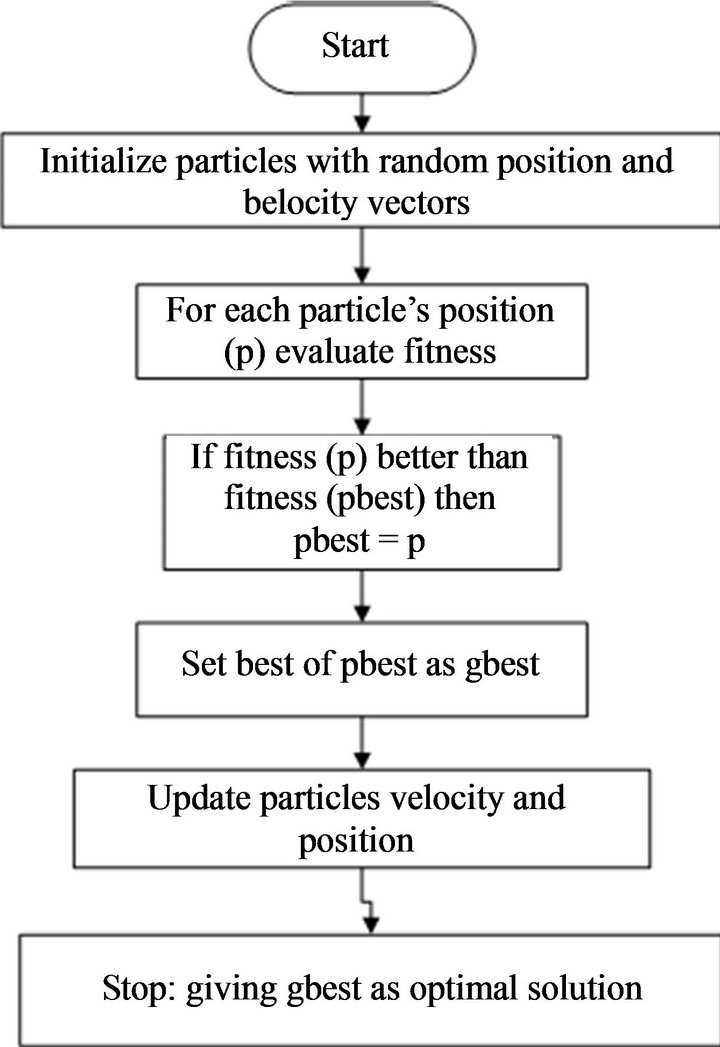
Figure 4. Proposed PSO algorithm for turbine control optimization.
rand: uniformly distributed random number between 0 and 1,
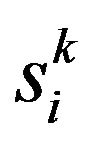 : current position of agent i at iteration k pbesti: pbest of agent igbest: gbest of the group.
: current position of agent i at iteration k pbesti: pbest of agent igbest: gbest of the group.
5. Proposed Algorithm
In Matlab, the particle swarm optimization (PSO) generates the set of swarm particles including the proportional gain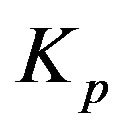 , integral gain
, integral gain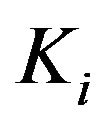 , and differential
, and differential 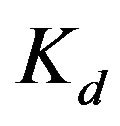 of PID control algorithm. The PID control gains are then sent to the Simulink environment where the steam turbine model is located. The model is simulated with the PID gains sent to Simulink and the results are sent back to Matlab workspace. The three performance measures including settling time
of PID control algorithm. The PID control gains are then sent to the Simulink environment where the steam turbine model is located. The model is simulated with the PID gains sent to Simulink and the results are sent back to Matlab workspace. The three performance measures including settling time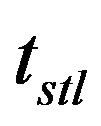 , rise time
, rise time 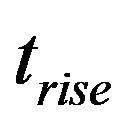 and overshoot
and overshoot 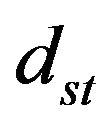 are evaluated from the simulation results. The fitness function value
are evaluated from the simulation results. The fitness function value 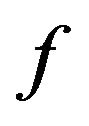 is calculated from the equation as follows
is calculated from the equation as follows
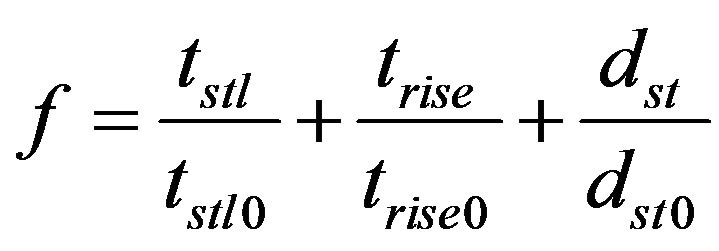 (8)
(8)
where, 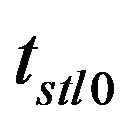 denotes the settling time,
denotes the settling time, 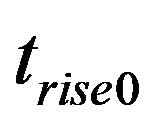 the rise time and
the rise time and 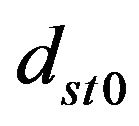 the overshoot of step response of the nominal steam turbine simulation. The optimization terminates if the convergence criteria is satisfied otherwise the fitness function values are sent back to SPO and sets of swarm particle are created for next loop of iteration.
the overshoot of step response of the nominal steam turbine simulation. The optimization terminates if the convergence criteria is satisfied otherwise the fitness function values are sent back to SPO and sets of swarm particle are created for next loop of iteration.
In the case of genetic algorithm (GA), similar procedure of SPO, as mentioned above, is continued with same set of design variables of PID control gains.
6. Simulation Results
In this research, a simple PID controller is designed and simulated using the methodology shown in Figure 2. Using particle swarm optimization (PSO) and genetic algorithm (GA), the control system is optimized separately to investigate their individually performances. The objective of the multi-criteria optimization problem is to minimize settling time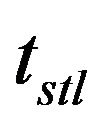 , rise time
, rise time 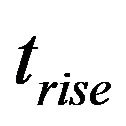 and overshoot
and overshoot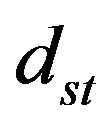 .Both optimization algorithms search for the optimal values of PID control gain, namely,
.Both optimization algorithms search for the optimal values of PID control gain, namely, 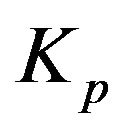 ,
, 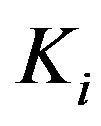 , and
, and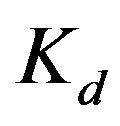 . In the baseline case, the PID control gains
. In the baseline case, the PID control gains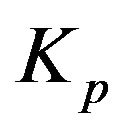 ,
, 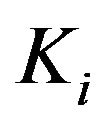 , and
, and 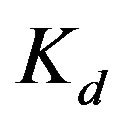 take the value of 0.5, 0.0001, and 0.05, respectively. In the baseline case, settling time
take the value of 0.5, 0.0001, and 0.05, respectively. In the baseline case, settling time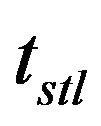 , rise time
, rise time 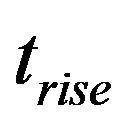 and overshoot
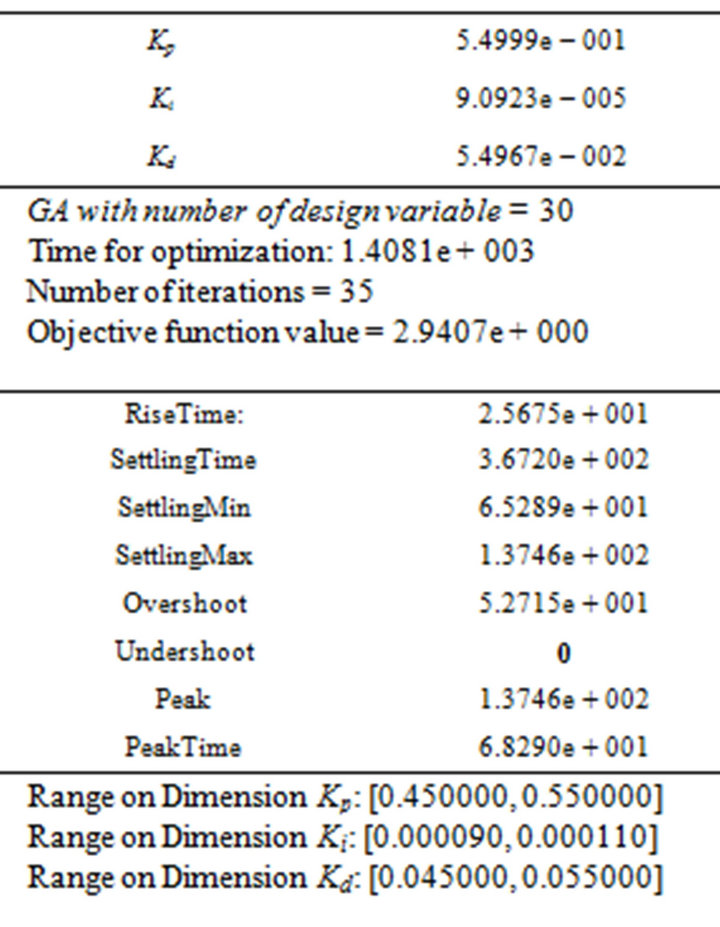
and overshoot 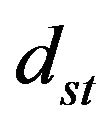 take the value of 382.77, 27.20, and 50.813, respectively. The result sets including rise time, settling time, overshoot/undershoot, peak time and with the other optimization parameters for PSO and GA are listed in Tables 1 and 2, respectively. In order to make both optimizations comparable, number of design variables in GA takes the value of 20 and so is that of swarm in PSO. The optimization is continued until 35 iterations in both cases.
take the value of 382.77, 27.20, and 50.813, respectively. The result sets including rise time, settling time, overshoot/undershoot, peak time and with the other optimization parameters for PSO and GA are listed in Tables 1 and 2, respectively. In order to make both optimizations comparable, number of design variables in GA takes the value of 20 and so is that of swarm in PSO. The optimization is continued until 35 iterations in both cases.
Figure 5 depicts the simulation result of response of baseline case of the PID controller for step input. Figure 6 represents one of the simulation results of the response after optimizing the PID controller with PSO. The settling time is improved by 4.37% by decreasing its value to 366.06 sec from the corresponding baseline value of 382.77 sec. To avoid the computational cost and optimization complexity, a narrow band of variation for the design variable set is chosen. Also the PID controller designed is a basic model of the conventional form.
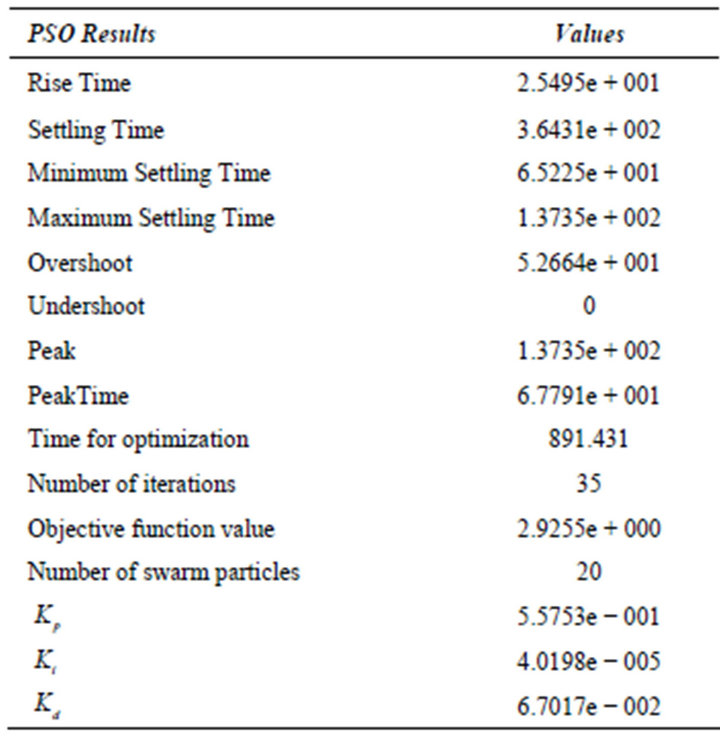
Table 1. Result set of PSO.

Table 2. Results set of GA.
Comparison of PSO and GA results are graphically represented in Figures 7-10. The optimization process has been carried out with different number of swarm/ population to compare both optimization algorithms. Figure 7 depicts that, for same number of swarm/population, the elapsed time to run the optimization algorithm is less in PSO in comparison to GA. Moreover, the settling and rise time of PSO are much lower than GA as shown in Figures 8 and 9, respectively. The results confirm that optimization of PID using PSO more efficient compared to GA.
Figure 10 represents the response of over overshoot versus number of warm and population size for PSO and GA, respectively. A close observation of the figure reveals that the overshoot of the step response in PSO, however, is higher with lower number of swarm. This does not affect the advantage of PSO over GA, since the practical implementation of PSO is with much higher number of swarms.
7. Conclusion
In this paper, a particle swarm optimization (PSO) and a genetic algorithm (GA) are separately implemented to optimize the gains of a proportional-integral-derivative (PID) algorithm to control a steam turbine. The results of both algorithms have been investigated and compared. The research has been performed with a simple PID controller to investigate the effectiveness of the algorithm
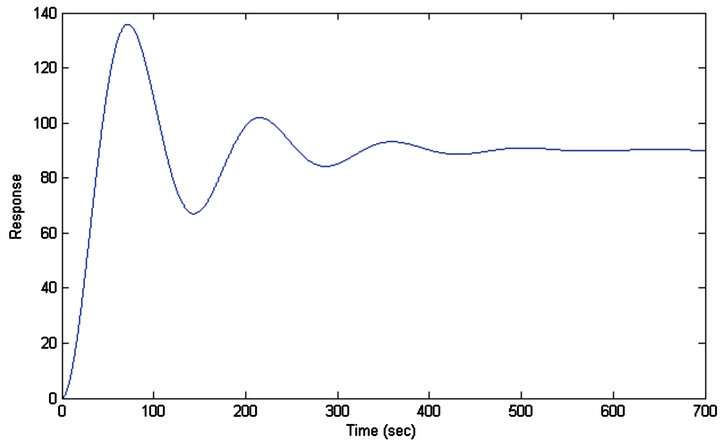
Figure 5. PID simulation result of time history of response without optimization.
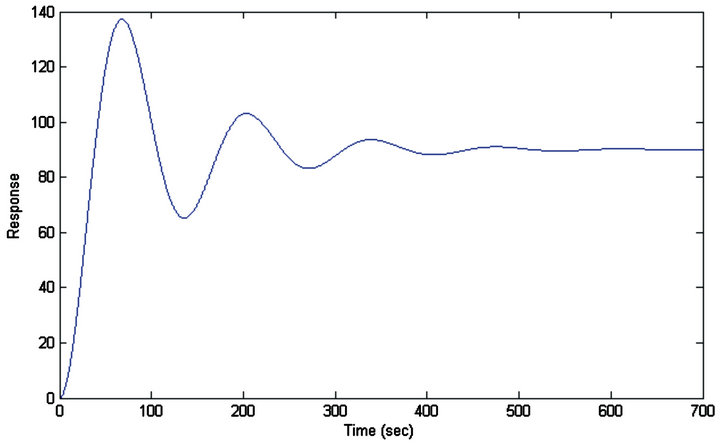
Figure 6. Simulation result of time history of optimal response (using PSO with, number of swarm = 20).
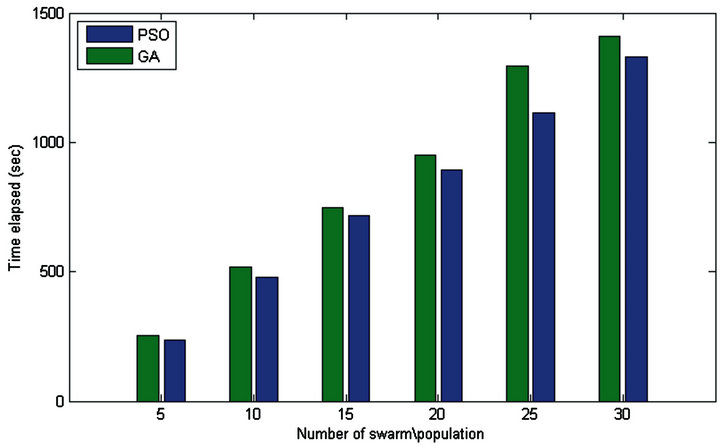
Figure 7. Comparison of PSO and GA for turbine control (time elapsed).
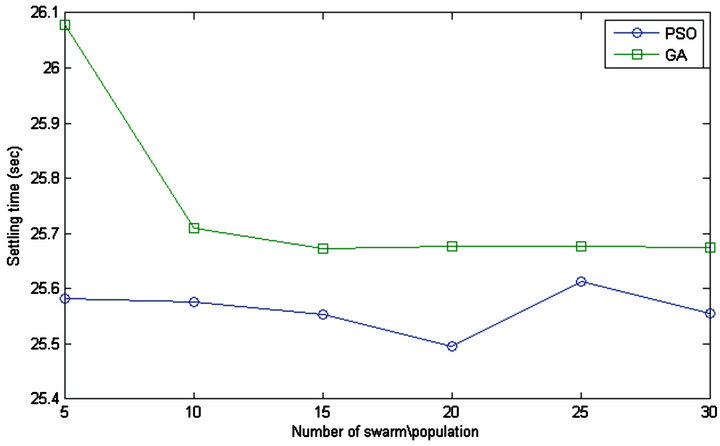
Figure 8. Comparison of PSO and GA for turbine control (setting time).
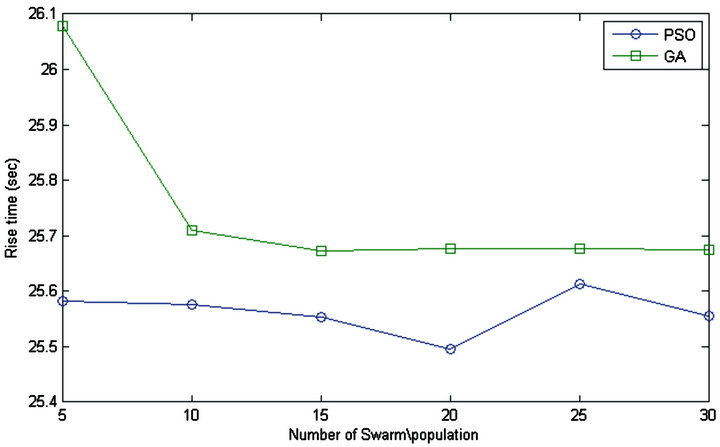
Figure 9. Comparison of PSO and GA for turbine control (rise time).
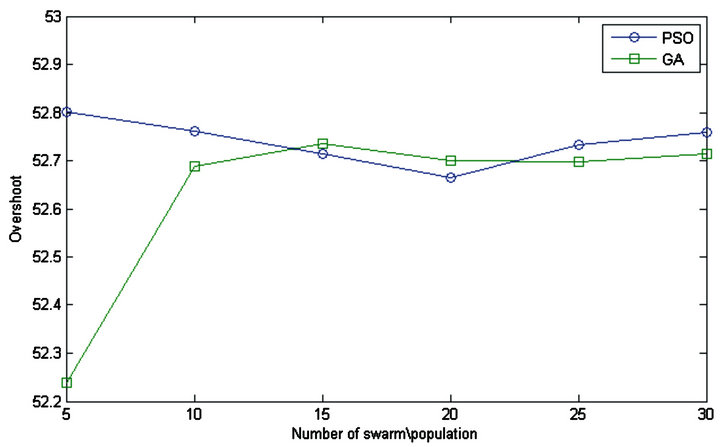
Figure 10. Comparison of PSO and GA for turbine control (overshoot).
while avoiding complexity and computational cost of the work. The goal of this paper was to evaluate the usefulness of PSO algorithm coupled with PID controller for steam turbine control and compare its function with a GA based PID controller. The numerical results validate the effectiveness of using PSO algorithm coupled with PID controller for the steam turbine control. The PSO-based PID controller was able to improve the optimization objective function by minimizing its value 0.51% lower than that of GA with spending 6.23% less time than GA. The PSO-based PID controller is highly recommended over GA-based PID controller. Future work may be performed with a more precise and practical PID controller for steam turbine control to optimize the output for better performance.
REFERENCES
- K. J. Astrom and T. Hagglund, “PID Controllers, Theory, Design and Tuning,” 2nd Edition, Instrument Society of America, 1995.
- O. Aydogdu and M. Korkmaz, “A Simple Approach to Design of Variable Parameter Nonlinear PID Controller,” International Conference on Advancement in Information Technology, Singapore, 2011.
- H. B. Liu, “Intelligent Coordinated Control of PowerPlant Main Steam Pressure and Power Output,” Journal of Systems Engineering and Electronics, Vol. 15, No. 3, 2004, pp. 350-358.
- J. A. Nelder and R. A. Mead, “A Simplex Method for Function Minimization,” Computer Journal, Vol. 7, No. 4, 1964, pp. 308-313.
- V. R. Sabanin, N. I. Smirnov and A. I. Repin, “Optimization of Settings of Regulative Devices in ASR,” Collection of Labours of Conference of Control, MEI, 2003, pp. 144-148.
- D. E. Goldberg, “Genetic Algorithms in Search Optimizations and Machine Learning,” Wesly, Addison, 1989.
- G. K. Voronovskiy, K. V. Makhotilo, S. N. Petrashev and S. A. Sergeev, “Genetic Algorithms, Artificial Neuron Networks and Problems of Virtual Reality,” Basis, Kharkov, 1997.
- C. L. Lin, H. Y. Jan and N. C. Shieh, “GA-Based Multi Objective PID Control for a Linear Brushless DC Motor,” IEEE/ASME Transactions on Mechatronics, Vol. 8, No. 1, 2003, pp. 56-65.
- M. Nasri, H. Nezamabadi-Pour and M. Maghfoori, “A PSO-Based Optimum Design of PID Controller for a Linear Brushless DC Motor,” World Academy of Science, Engineering and Technology, Vol. 20, 2007, pp. 211- 215.
- D. B. Fogel, “Evolutionary Computation toward a New Philosophy of Machine Intelligence,” IEEE, New York, 1995.
- J. Kennedy and R. Eberhart, “Particle Swarm Optimization,” Proceedings of IEEE of International Conference on Neural Networks, Vol. 4, Perth, 1995, pp. 1942-1948. doi:10.1109/ICNN.1995.488968
- A. Banks, J. Vincent and Ch. Anyakoha, (2007) “A Review of Particle Swarm Optimization. Part I: Background and Development,” Natural Computing, Vol. 6, No. 4, pp. 467-484. doi:10.1007/s11047-007-9049-5
- M. A. Abido, “Optimal Design of Power-System Stabilizers Using Particle Swarm Optimization,” IEEE Transactions on Energy Conversion, Vol. 17, No. 3, 2002, pp. 406-413. doi:10.1109/TEC.2002.801992
- J. Yang and A. Bouzerdoum, “A Particle Swarm Optimization Algorithm Based on Orthogonal Design,” IEEE Congress on Evolutionary Computation, 18-23 July 2010.
- PSO Tutorial, 2012. http://www.swarmintelligence.org/tutorials.php
Appendix
Different Optimization Results:
Without Optimization:
Output value:

Results:
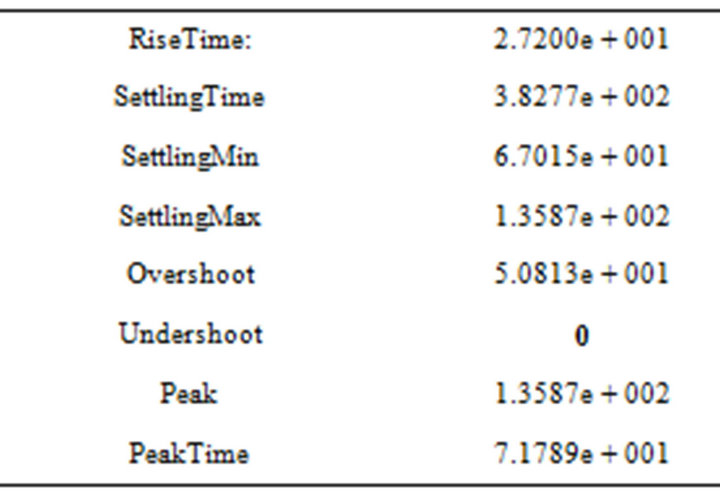
With PSO Optimization:
PSO with number of swarm particles = 5
Time for optimization: 237.5975
Number of iterations = 35
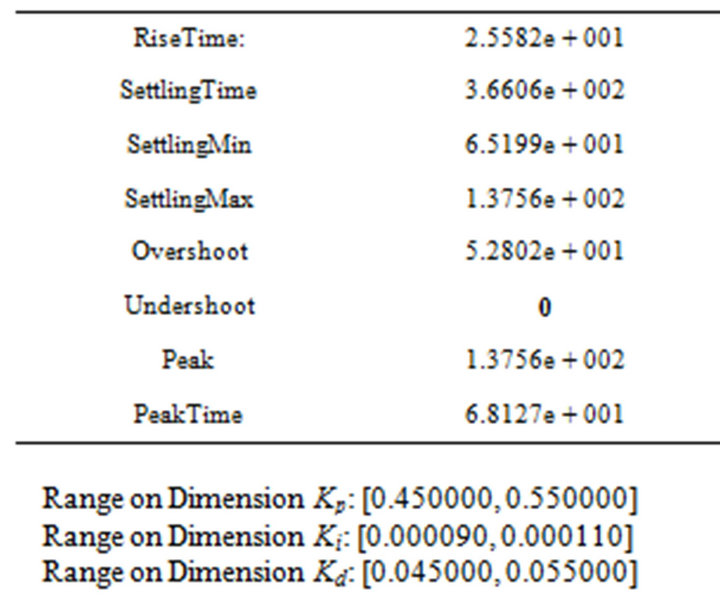
Optimized Output Value:
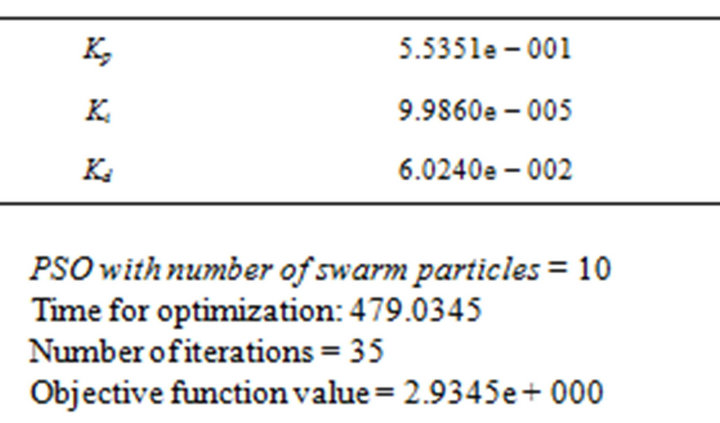
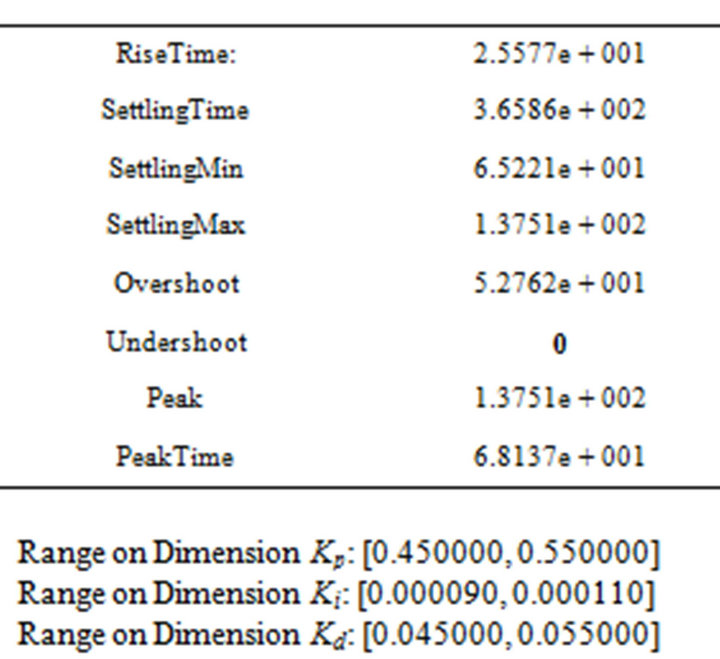
Optimized Outputvalue:
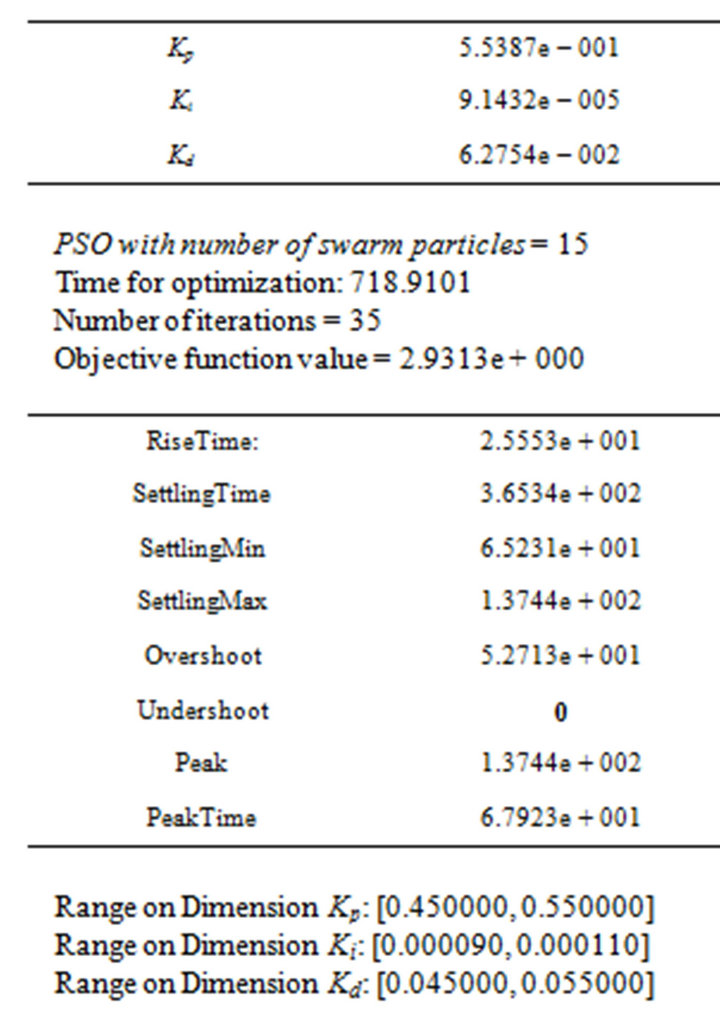
Optimized Output Value:

Optimized Output Value:
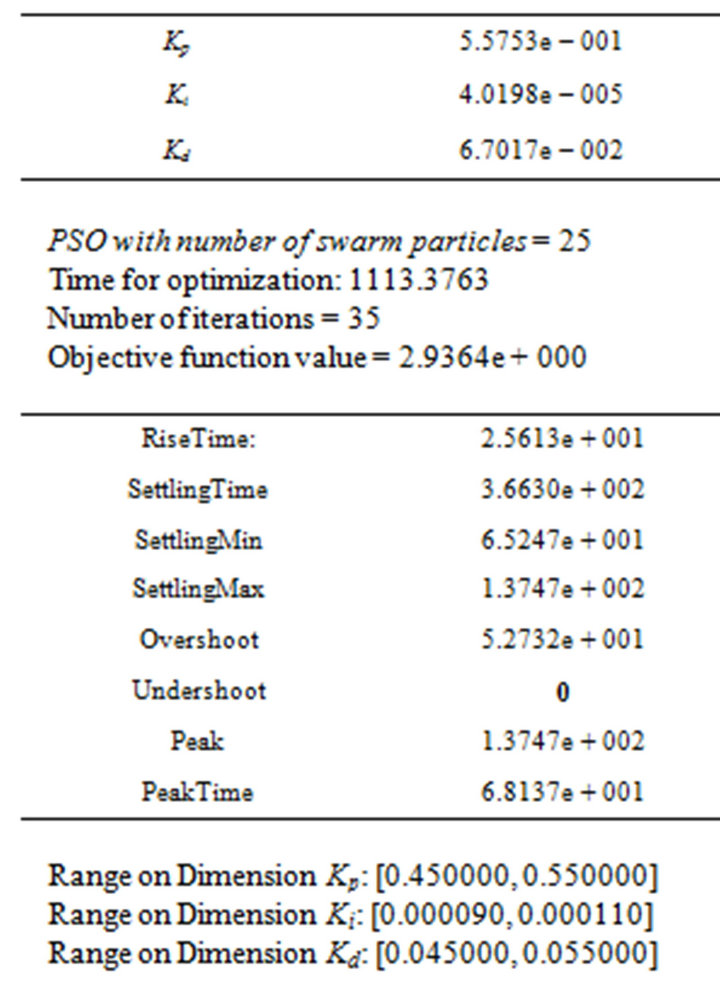
Optimized Output Value:
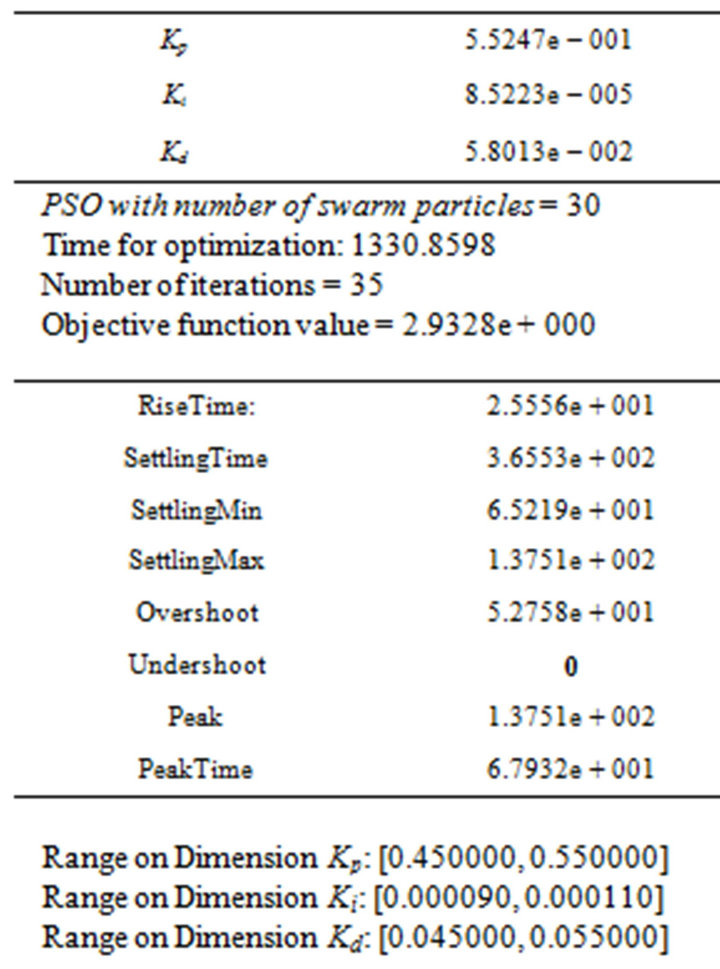
Optimized Output Value:

Optimized Output Value:

Optimized Output Value:
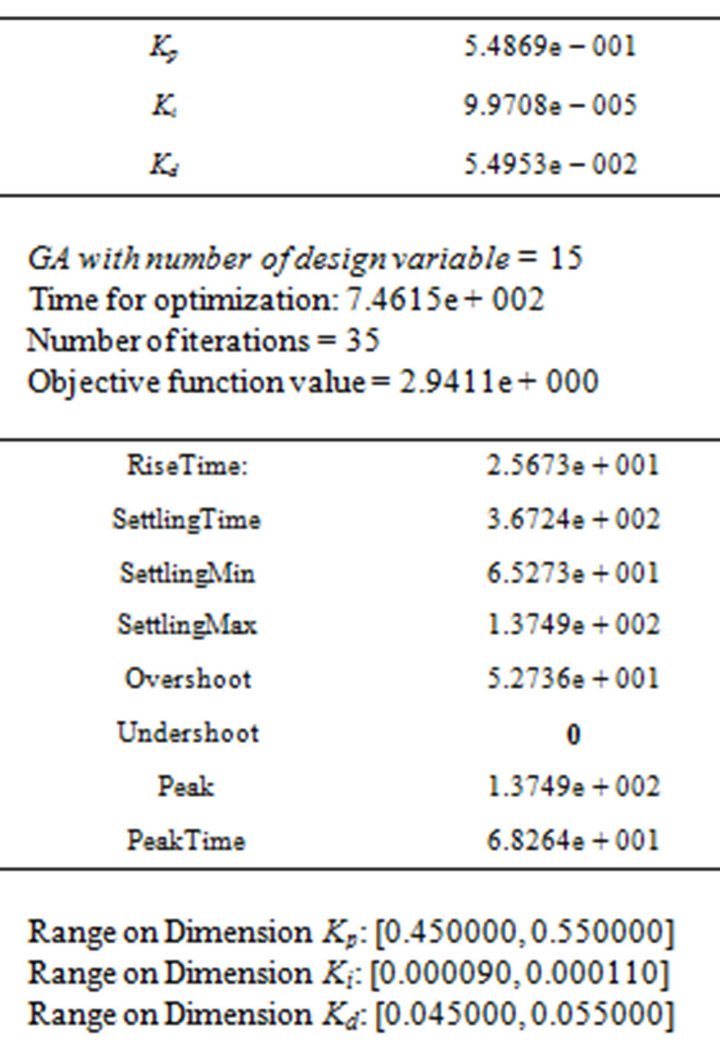
Optimized Output Value:

Optimized Output Value:

Optimized Output Value:
Optimized Output Value:

NOTES
*Corresponding author.

