Materials Sciences and Applications
Vol.06 No.07(2015), Article ID:57927,11 pages
10.4236/msa.2015.67065
ND:YAG Laser Pulses Ablation Threshold of Stainless Steel 304
Mitra Radmanesh, Amirkianoosh Kiani*
Department of Mechanical Engineering, University of New Brunswick, Fredericton, Canada
Email: *a.kiani@unb.ca
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 April 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
Laser processing and laser surface texturing in multiple fields have become a popular topic of study in recent decades. Understanding the principles behind the laser irradiation mechanism is an essential step in choosing the most effective process parameters. Through this study, the effects of power and pulse duration on the structure and surface pattern of stainless steel type 304 were examined, and optimized laser parameters were introduced for desired laser penetration and heat-affected areas on the surface. The analyzed sample was prepared by using variations of pulse durations and different pulsed energies. Looking at the trend of change of non-dimensional temperature along the surface, thickness, and center of the sample, the effects of pulse duration and intensity (corresponding to energy) were observed. Upon considering all the aspects of the irradiated spots, such as heat-affected area diameter, surface patterns, and penetration depth, the advantages and disadvantages of short and long pulse durations are mapped out clearly. Also, a new method to obtain the ablation threshold of stainless steel is introduced, and a thorough analytical solution is obtained.
Keywords:
Laser Material Processing, Laser Surface Treatment, Stainless Steel, Ablation Threshold

1. Introduction
In recent decades, lasers involving technologies and modeling of laser material interactions have gained notable attention in micro/nano manufacturing fields. Some of the most important applications of lasers are treatment and processing of variety of metals and alloys. Laser material processing involves high concentrated heating of solid targets using lasers to enable several types of structural changes, such as amorphization, hardening, and surface patterning, in a fast and precise manner, in micro, sub-micro, and nano scales [1] [2] . Lasers are able to deliver a range of very low to extremely high energy with extreme precision in dimension, spatial, and temporal distribution. In comparison to conventional methods, this laser approach is more flexible and reduces processing time, making it particularly suitable for both mass production and rapid prototyping and custom-scale manufacturing for a wide variety of applications such as micro-welding, drilling, cutting, and heat treatment of metals and alloys [3] [4] .
Laser processing can be applied in two categories based on the energy requirements: applications that require relatively low energy with limited structural and physical changes, such as annealing of semiconductors, and applications that call for high energy transforms for significant structural changes over a large volume, such as welding [5] . Energy transformation in any application involving lasers is fully dependent on the nature of the interacting material and its chemical bonding. In recent decades, there have been significant improvements, by development of ultra-short lasers, to increase the interaction time (pulse duration) between the laser and the material, hence reducing the effects on the bulk material [2] [6] . Despite these improvements, ultra-short laser systems are very expensive and cannot be utilized in industries. Therefore, depending on the nature of the application, less expensive laser systems with various pulse durations in the range of millisecond to microsecond that are widely available in manufacturing sectors are more popular among the manufacturers. A thorough understanding of the laser irradiation mechanism is required to utilize the more common lasers to their fullest efficiency.
In order to fully understand the mechanism behind laser irradiation as well as to increase the efficiency of the process, understanding the effects and controlling the process parameters is of utmost importance; therefore, choosing the most optimal pulse duration is essential to the final quality of a particular application [2] [7] . This study was conducted to identify the effects of key laser process parameters, such as power and pulse duration, in industrial laser systems on the structure and surface pattern of stainless steel 304, in order to develop an optimal process map for laser processing and surface texturing of materials. Also, a new method for calculation of ablation threshold has been introduced for stainless steel, which can be customized for other metals and alloys.
2. Experimental Setup
Thin sheets of stainless steel type 304, with thickness of 0.5 mm were used for surface treatment in this study. The sample was irradiated with microsecond pulses to create the predetermined bullet-point patterns across its surface. Experiments were conducted using a pulsed Nd:YAG laser system with a peak power of 6 kW, and beam diameter of 20 um. For a wavelength of 1064 nm provided by this laser system, a coefficient of absorption of 0.3 was used for stainless steel type 304 throughout the calculations [8] [9] .
The study was completed using variations of intensity of the laser system. The delivered intensity was controlled by reducing the voltage at 25 intervals starting at 400 V to 275 V. This trend was applied to three different pulse durations of 20 ms, 10 ms, 5 ms. Table 1 visualizes the procedure of the experiment:
This experiment provided a very confined and controlled experimental environment for the required observations.
Upon completing the experiment, the effects of power and pulse duration on the surface structure, heat-af- fected zone on the surface, depth of penetration, and the created surface patterns were fully examined. After obtaining a thorough map of effects of process parameters, a series of optimal parameters are presented based on the observations.
Table 1. Laser parameters of laser processing of stainless steel.
3. Methodology
Since laser processing mainly involves transformation hardening (which is dominantly a heat transfer process), examining the temperature distribution and modeling the thermal process from the initial stages of heating is an effective method to investigate the connection of process parameters with the desired outcome results [10] [11] . Ideally, the size and shape of the irradiated zone is required to analyze the obtained results. This information cannot be extracted directly by using the process parameters; thus, temperature history of the process must be developed to obtain the heat-affected profile of the work piece [12] . To develop the temperature history of the irradiated sample, the nondimensionalization method was introduced to track the changes due to each laser parameter, by calculating the non-dimensional temperature at the surface, depth, and center where the maximum non-dimensionaltemperature occurs [13] -[15] . This method is a simple technique for tracking the trend of changes occurring in laser irradiation, and is an effective step in investigating the effects of laser parameters upon the heat-affected profile [4] [16] .
To proceed with this method, a cylindrical symmetric flow without internal heat generation, and constant, isotropic material properties was assumed; from there, a transient heat conduction equation and a proper boundary condition, as shown in the following, were defined to develop the temperature history of the process to estimate the temperature at each point [17] .
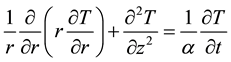 (1)
(1)
where 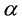 is the thermal diffusivity, and is defined as
is the thermal diffusivity, and is defined as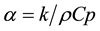 , with k being the thermal conductivity, and
, with k being the thermal conductivity, and 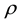 the density, and
the density, and 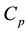 the specific heat.
the specific heat.
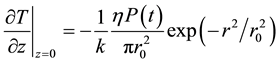 (2)
(2)
where  is defined as the peak power delivered,
is defined as the peak power delivered,  is the fraction of energy absorbed by the surface, and
is the fraction of energy absorbed by the surface, and 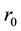 is the beam radius (in this study the beam diameter is 20 um)
is the beam radius (in this study the beam diameter is 20 um)
Taking into account the vast range of scale variation between the required parameters (for example, while temperature changing is in orders of thousands of degrees, pulse duration only changes in orders of milliseconds), it is more convenient to define a set of non-dimensional groups, and to simplify the obtained equations in terms of temperature, radius, location of the spot, and the required constant values [11] [17] . The customized non-dimensional variables are as follow:
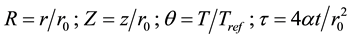
where, 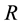 is non-dimensional radius,
is non-dimensional radius, 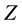 is non-dimensional depth,
is non-dimensional depth, 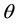 is non-dimensional temperature (It is assumed that reference temperature is the melting temperature of the material), and finally,
is non-dimensional temperature (It is assumed that reference temperature is the melting temperature of the material), and finally, 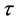 is non-dimen- sional time for
is non-dimen- sional time for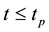 .
.
These non-dimensional variables are then used to simplify Equations (1) and (2). Equation (3) displays the simplified boundary equation [12] :

where Q is the non-dimensional power and is defined as:
Taking the Laplace transform of the redefined heat conduction equation, and solving the resultant differential equation, we can then calculate the integral form of the temperature. Hence, the maximum surface temperatures of various pulse durations can be obtained to show the non-dimensional temperature profiles under each condi- tion. As stated, the non-dimensional temperature in this study was tracked along the radius, thickness, and center of the work piece. Equations (4)-(6) define these temperature profiles [12] [17] :



Comparing the temperature profiles of each case can consequently lead to estimating the most optimal process parameters for more efficient laser processing applications.
An important theory to be considered when working with non-dimensional temperatures is the behaviour of the temperature profile in cases of constant power and constant energy. When looking at a constant power case, a shorter pulse duration results in a lower non-dimensional temperature [16] . This is because when constant power is delivered by the laser system, a shorter irradiation ime results in less heat being accumulated, and a lower non-dimensional temperature is achieved. On the other hand, when considering a constant energy case, the non-dimensional temperature is higher with shorter pulse durations [16] . This can be explained by the fact that with a constant amount of energy, a shorter pulse duration allows the energy less time to spread along the work piece. In other words, energy is delivered in a more concentrated manner with shorter pulse durations; hence, higher non-dimensional temperatures resulted. With this behaviour in mind, experimental observations were examined to determine the most optimal process parameters [16] .
4. Results and Discussion
4.1. Heat Affected Zones and Keyhole Generation
Multiple bullet point patterns with stated properties are created upon the surface of the indicated stainless steel sample. Figure 1 displays the optical images taken of the first four points of 20 ms, 10 ms, and 5 ms pulse durations, respectively. As displayed, the size and surface texture of each spot changes based on the corresponding intensity and pulse duration.
Each irradiated spot displays different layers and patterns across its surface. This creation of different zones on the surface is due to the keyhole generation phenomenon that takes place during any laser surface texturing process [9] [18] . In Figure 1, each picture is almost consisted of three zones; Figure 2 displays these zones and creation of keyhole in more details. Figure 2(a) presents the different zones created across the surface. The outer area, which is indicated with the solid circle, marks the secondary heat-affected zone. The next layer shown with the dashed circle indicates the primary heat-affected zone (HAZ), and is the center of the penetration zone. Lastly the shaded area (molten area), which appears as waves on the surface of the irradiated spot, signifies the molten area caused by the accumulation of heat on the surface of the work piece [9] [19] .
Figure 2(b) presents the location of keyhole generation with respect to the zones created across the irradiated spot. In this figure, the white triangle is the primary heat-affected zone, the shaded area is the molten area, and
Figure 1. Optical images of irradiated spots (scale bar: 30 µm).
Figure 2. Surface zones and keyhole generation (scale 10 um).
larger triangle signifies the secondary heat-affected zone. When processing materials using a laser, controlling the size of each of these layers is an essential factor in the precision and quality of the final results. Hence, it is essential to identify the effects of intensity and pulse duration on these layers [9] [19] . The keyhole is generated in the white triangle at the center of the irradiated spot, which corresponds to the primary heat-affected zone.
4.2. Non-D Temperature Profile: Variation of Heat Affected Zones
The effects of power and pulse duration on the size of each indicated zone can be further examined by looking at the non-dimensional temperature profiles of various pulse durations across the corresponding outer diameters (primary heat-affected zone). Figure 3 illustrates the variation of the outer diameter (as indicated in Figure 2) based on intensity values.
It is important to note that in this study intensity is obtained based on the energy delivered to the sample. As expected, the diameter of the heat-affected zone increases with an increase in intensity, hence an increase in the delivered energy. At a constant intensity (energy per area), the shorter pulse duration results in a larger outer diameter. A case of a constant intensity limits the amount of available energy; therefore, when using shorter pulse duration, the constant energy will be delivered in a more concentrated manner, since the process is not long enough for the energy to spread across the material. This in turn results in a more heat accumulation, and therefore a larger heat-affected zone diameter is achieved using shorter pulse duration [16] .
After examining the behaviour of the outer diameter, in accordance to intensity and pulse duration, exploring it at various key points is essential in understanding this behaviour. The important zones at which significant changes occur in the behaviour of outer diameter are indicated in Figure 4. Starting with Zone 1, the trend of changes is as expected, and as theory suggests, the outer diameter increases with an increase in intensity, and shorter pulse duration results in a larger diameter value at a constant intensity. However, when zone 2 is reached, it can be seen that the diameters start to have similar values, particularly for 10 ms and 20 ms pulse durations. This turn of events suggests that the effects of pulse duration on the heat-affected zone start to decrease as the intensity increases. This indicates that the temperature of the material is starting to reach the ablation temperature
Figure 3. Outer diameter vs. intensity.
Figure 4. Computed results for ablation threshold (Equation (9)).
threshold, and that the material is reaching the saturation state. Laser ablation is generally defined as material removal in macroscopic scale from the surface of the work piece, due to a significant change of state, where the ablated amount transforms into the gas or plasma phase [20] [21] . In cases where laser radiation reaches a sufficiently high intensity, the surface of the material begins to ionize and transforms into a form of dense plasma. When the delivered energy by the laser is increased while the pulse duration is decreased, the accumulated heat will eventually exceed the breakdown threshold of the material. Thus, ablation is expected, and the size of heat-affected zone (HAZ) reaches its saturation point [21] . Looking at zone 3, it is clear the material has reached the saturation point, and the diameter remains constant despite the changes in intensity. Reaching the saturation point suggests the material has exceeded its ablation threshold at this point, and as the intensity increases the material starts evaporating;, consequently, the diameter of the heat-affected zone remains constant [22] . Determining the threshold for ablation temperature is very essential in laser processing of materials.
4.3. Ablation Threshold of Stainless Steel
In this work, a method to develop the ablation threshold of stainless steel along with a thorough analytical procedure is presented. This method can be further customized to accommodate the ablation thresholds of any other metals and alloys.
For lasers with Gaussian beam profile, if heat propagation effects are neglected, the feature size of the ablated area can be calculated by [23] [24] :

where, rO is the radius of laser spot, φth(Ns) is the multi-pulse ablation threshold which depends both on the number of pulses and material and φO is the maximum laser flounce which is given by:

From Equations (7) and (8), the one pulse ablation threshold of the stainless steel can be calculated by:

Figure 4 shows the computed results for φth(1) at different pulse durations based on the analytical solution. As shown in the figure, the ablation threshold for one pulse decreases with decrease in the pulse duration. Also, the threshold nearly reaches zero at diameter of 60 um which is in a good agreement with our experimental results shown in Figure 3.
Depending on the application required, the intensity and pulse duration could be varied and controlled in order to reach or avoid the ablation threshold and achieve the desired results in any of the presented zones.
4.4. Relation of Maximum Non-D Temperature, Intensity, and Non-D Power
The trend of change in heat-affected zones can be further explained by looking at the relation between the maximum non-dimensional temperature, intensity, and non-dimensional power used with each indicated pulse durations. Figure 5 presents this comparison.
Figure 5, the non-dimensional temperature, increases with an increase in both intensity and power. Thus, at higher intensity and power values, higher temperature is delivered to the materials, and a larger area is affected. This is in close agreement with the changes occurring in the outer diameter based on energy and intensity.
Figure 5. Max non-dtemperature vs. intensity & non-d power (Equations (4)-(6)).
Looking closely at graph 1), at a constant non-dimensional power, shorter pulse duration results in a lower non-dimensional temperature. However, in graph 2) the opposite is observed: at a constant intensity, the shorter pulse duration develops a higher non-dimensional temperature. This corresponds with the behaviour of the outer diameter at different pulse durations and intensity values presented in Figure 3. It is clear the higher non-di- mensional temperatures result in larger heat-affected areas, and at a constant intensity the shorter pulse duration results in both higher non-dimensional temperature and larger outer diameter. Shorter pulse duration causes the delivered energy to be more concentrated on the irradiated spot, and hence increases the accumulated heat [16] .
4.5. Non-D Temperature Profile; Surface, and Depth
4.5.1. Effects of Laser Parameters on Surface Patterns
The next portion of the study mainly concentrated on the changes in non-dimensional temperature along the surface and depth of the work piece. According to Figure 2, both outer and inner diameters change relative to each other with intensity and pulse durations. To demonstrate this relativity, Figure 6 displays the changes in the ratio of diameters with intensity. The outer to inner diameter ratio increases with an increase in intensity. This means that as more energy is delivered to the material, the heat-affected zone grows and inner diameter decreases, resulting in a larger molten zone area. It should also be noted that looking at a constant intensity, the shorter pulse duration results in a larger diameter ratio, which is in a close agreement with the previous analytical results.
In Figure 2, it was observed that the indicated molten area appears as a range of waves on the surface of the irradiated spot. When a material surface is irradiated using a pulsed laser system, several physical processes such as desorption, melting, vaporization, boiling, or even spontaneous evaporation (ablation) may take place that could result in formation of wave-like topography on the surface of the material [22] . Multiple theories present the reasons for these periodic structures appearing upon the surface of the irradiated material, but they have mainly been related to the capillary waves [22] .
Surface pressure gradient could be an initiative for the formation of these structures. It is known that the pressure near the concave portion of a surface of a material is larger than on the convex parts. Upon melting of the surface material due to laser irradiation, this pressure difference could cause the molten liquid to move towards the convex regions of the surface, resulting in the creation of wave-like patterns [25] . Another possibility could be the non-homogenous deposition of energy that would initiate the motion of the molten material from hotter regions to colder areas. However, the key element that is common in both cases is the motion of the molten material to increase the amplitude of the wave-like structures. This is contrary to the tendency of molten material for a wetting of its own solid, and is due to the existing surface forces acting on the liquid. This results in creation of the wave-like patterns on the surface of the material [26] .
Figure 6. Outer to inner diameter ratio vs. intensity.
4.5.2. Non-D Temperature along the Surface
To further understand the relation among the outer and inner diameter due to the variation of laser parameters effects, the non-dimensional temperature along the surface is examined. Figure 7 demonstrates this variation along the surface. The non-dimensional surface temperature is at its maximum at the center of the irradiated spot, gradually decreases along the radius of the spot, and eventually reaches a constant value at the room temperature. The three layers created on the surface of the irradiated spot can easily be shown along these curves. As indicated in the figure by the lines on the curves, the middle zone corresponds to the molten area shown in Figure 2.
As presented in the experimental results, at shorter pulse durations the secondary heat-affected zone (molten area) is significantly smaller than with the longer pulse durations; this can clearly be seen in Figure 7, as the solid line which is an indicator for pulse duration of 5 ms has the smallest part in the middle section of the curves compared to the dashed lines. A shorter pulse duration delivers the energy in a more concentrated manner; hence, shorter pulse durations involve rapid energy deposition and creation of vapour and plasma phases, and result in absence of molten area [25] . This reduces the effects of energy on the surrounding of the target area (heat accumulation). Therefore, the non-homogenous aspect of energy deposition is reduced, which causes the creation of wave-like patterns. It can be concluded that shorter pulse durations result in a better surface resolution, and smaller heat-affected zone [25] .
4.5.3. Effects of Laser Parameters on Depth and Penetration & Non-D Temperature Profile at Depth
After examining the changes across the surface of the sample, it is essential to look at the effects of laser parameters, particularly pulse duration, on depth and penetration of metals. Figure 8 demonstrates the trend of change in the non-dimensional temperature along the thickness (depth) of the sample with regards to intensity. It also displays the variation of the heat-affected zone at the back of the sample to the outer diameter ratio with intensity.
In Figure 8(a), the non-dimensional temperature increases as the intensity increases. This indicates that the penetration depth increases at higher intensities, which is in agreement with expectations: higher intensity delivers higher energy to the material; hence the laser affects a larger amount of the material. As with previous cases, if we consider a case of constant intensity, it can be seen that the shorter pulse duration results in a higher non- dimensional temperature at the depth as well; hence a deeper penetration is achieved. This is further supported by looking at the heat-affected area on the back of the sample, which is displayed in Figure 8(b); this graph presents the change in the heat-affected zone on the back of the sample as the intensity increases [12] . Back to outer diameter increases when increasing the intensity, which indicates that the heat-affected zone on the back of the samples increases with intensity as well. Therefore, in order to achieve a better surface resolution and a clearer and deeper penetration, shorter pulse durations should be used in the applications. However, with applications that take place on the surface of the material, such as surface annealing of stainless steel, larger pulse durations should be used since they resulted in a larger heat-affected zone on the surface of the materials [12] .
Figure 7. Non-dimensional temperature across the surface (Equation (4)).
Figure 8. Non-D temperature at depth (Equation (5)) & back to outer diameter ratio vs. intensity.
5. Conclusion
A stainless steel type 304 sample was used to investigate the effects of pulse duration and power on the surface structure, patterns, and penetration, during laser irradiation. Also, a method for obtaining the ablation threshold of stainless steel for one pulse was introduced, which could be customized for any other metals and alloys. After a thorough analysis, it was observed that pulse duration was an essential factor in controlling the quality of the final product. In order to obtain a better surface resolution with minimum damage to the surrounding areas of the irradiated spot, shorter pulse durations should be used. For applications involving surfaces, larger pulse durations are recommended due to their larger heat-affected zone diameters. Adjusting the intensity, that is, the energy delivered to the material, can control the depth of the penetration. Further, the introduced method for the ablation calculation showed that the ablation threshold for one pulse decreased with decrease in the pulse duration, and that the results were in very close agreement to the obtained experimental results.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Cite this paper
MitraRadmanesh,AmirkianooshKiani, (2015) ND:YAG Laser Pulses Ablation Threshold of Stainless Steel 304. Materials Sciences and Applications,06,634-645. doi: 10.4236/msa.2015.67065
References
- 1. Majumdar, J. and Manna, I. (2011) Laser Material Processing. International Materials Reviews, 56, 341-388.
http://dx.doi.org/10.1179/1743280411Y.0000000003 - 2. Ahmmed, T., Yang, E.J., Ling, P., Servio B. and Kietzig, A. (2014) Introducing a New Optimization Tool for Femtosecond Laser-Induced Surface Texturing on Titanium, Stainless Steel, Aluminum and Copper. Optics and Lasers in Engineering, 66, 258-268.
http://dx.doi.org/10.1016/j.optlaseng.2014.09.017 - 3. Harooni, M., Carlson, B., Strohmeier, B.R. and Kovacevic, R. (2014) Pore Formation Mechanism and Its Mitigation in Laser Welding of AZ31B Magnesium Alloy in Lap Joint Configuration. Materials & Design, 58, 265-276.
http://dx.doi.org/10.1016/j.matdes.2014.01.050 - 4. Brügmann, M.H. and Feurer, T. (2014) Comparative Theoretical Analysis of Continuous Wave Laser Cutting of Metals at 1 and 10 μm Wavelength. Applied Physics A, 116, 1353-1364.
http://dx.doi.org/10.1007/s00339-014-8233-6 - 5. Qiu, F., Uusitalo, J. and Kujanpaa, V. (2012) Laser Transformation Hardening of Carbon Steel: Microhardness Analysis on Microstructural Phases. Surface Engineering, 29, 34-40.
- 6. Rizvi, N.H. (2003) Femtosecond Laser Micromachining: Current Status and Applications. Riken Review, 107-112.
- 7. Rulliere, C.E. (2005) Femtosecond Lasers; Principles and Experiments. Springer, Berlin.
http://dx.doi.org/10.1007/b137908 - 8. Kuang, J.H., Hung, T.P., Lai, K., Hsu, C.M. and Lin, A.D. (2012) The Surface Absorption Coefficient of S304L Stainless Steel by Nd:YAG Micro-Pulse Laser. Advanced Materials Research, 472, 2531-2534.
- 9. Kazemi, K. and Goldak, J.A. (2009) Numerical Simulation of Laser Full Penetration Welding. Computational Materials Science, 44, 841-849.
http://dx.doi.org/10.1016/j.commatsci.2008.01.002 - 10. Tran, D.V., Lam, Y.C., Zheng, H.Y., Murukeshan, V.M., Chai, J.C. and Hardi, D.E. (2004) Femtosecond Laser. Processing of Crystalline Silicon, 19, 11.
- 11. Yilbas, B.S. and Al-Aqeeli, N. (2009) Analytical Investigation into Laser Pulse Heating and Thermal Stresses. Optics & Laser Technology, 41, 132-139.
http://dx.doi.org/10.1016/j.optlastec.2008.05.016 - 12. Kiani, A., Venkatakrishnan, K. and Tan, B. (2013) Optimal Absorption Enhancement in 3D Silicon Oxide Nano-Sand-wich Type Solar Cell. Optics Express, 22, A120-A131.
- 13. Ashby, M.F. and Easterling, K.E. (1984) The Transformation Hardening of Steel Surfaces by Laser Beams—I. Hypo-Eutectoid Steels. Acta Metallurgica, 32, 1935-1937.
http://dx.doi.org/10.1016/0001-6160(84)90175-5 - 14. Li, W.B., Easterling, K.E. and Ashby, M.F. (1986) Laser Transformation Hardening of Steel—II. Hypereutectoid Steels. Acta Metallurgica, 34, 1533-1543.
http://dx.doi.org/10.1016/0001-6160(86)90098-2 - 15. Ion, J.C., Scherclift, H.R. and Ashby, M.F. (1992) Diagrams for Laser Materials Processing. Acta Metallurgica et Materialia, 40, 1539-1551.
http://dx.doi.org/10.1016/0956-7151(92)90097-X - 16. Kiani, A., Venkatakrishnan, K. and Tan, B. (2011) Enhancement of the Optical Absorption of Thin-Film of Amorphorized Silicon for Photovoltaic Energy Conversion. Solar Energy, 85, 1817-1823.
http://dx.doi.org/10.1016/j.solener.2011.04.020 - 17. Woodard, P. and Druden, J. (1998) Thermal Analysis of a Laser Pulse for Discrete Spot Surface Transformation Hardening. Journal of Applied Physics, 85, 2488-2496.
- 18. Tenner, F., Brock, C., Klampfi, F. and Schmidt, M. (2014) Analysis of the Correlation between Plasma Plume and Keyhole Behavior in Laser Metal Welding for the Modeling of the Keyhole Geometry. Optics and Lasers in Engineering, 64, 32-41.
http://dx.doi.org/10.1016/j.optlaseng.2014.07.009 - 19. Hocheng, H., Tsai, H.Y., Jadhav, U.U., Wang, K.Y. and Lin, T.C. (2014) Laser Surface Patterning. Comprehensive Materials Processing, 9, 75-113.
http://dx.doi.org/10.1016/B978-0-08-096532-1.00917-1 - 20. Linde, V.D. and Sokolowski-Tinten, K. (1999) The Physical Mechanisms of Short-Pulse Laser Ablation. Applied Surface Science, 154-155, 1-10.
http://dx.doi.org/10.1016/S0169-4332(99)00440-7 - 21. Nolte, S., Momma, C., Jacobs, H. and Tunnermann, A. (1997) Ablation of Metals by Ultrashort Laser Pulses. Journal of the Optical Society of America B, 14, 2716-2722.
http://dx.doi.org/10.1364/JOSAB.14.002716 - 22. Dobrzanski, L.A. and Drygala, A. (2007) Laser Processing of Multicrystalline Silicon for Texturization of Solar Cells. Material Processing Technology, 191, 228-231.
http://dx.doi.org/10.1016/j.jmatprotec.2007.03.009 - 23. Venkatakrishnan, K., Stanley, P., Sivakumar, N.R., Tan, B. and Lim, L.E.N. (2003) Effect of Scanning Resolution and Fluence Fluctuation on Femtosecond Laser Ablation of Thin Films. Applied Physics A, 77, 655-658.
http://dx.doi.org/10.1007/s00339-002-1668-1 - 24. Borowiec, A. and Haugen, H.K. (2004) Femtosecond Laser Micromachining of Grooves in Indium Phosphide. Applied Physics A, 79, 521-529.
http://dx.doi.org/10.1007/s00339-003-2377-0 - 25. Erdogan, M., Oktem, B., Kalaycioglu, H. and Yavas, S. (2011) Texturing of Titanium (Ti6A14V) Medical Implant Surfaces with Mhz-Repetition-Rate Femtosecond and Picosecond Yb-Doped Fiber Lasers. Optic Express, 19, 10986-10996.
http://dx.doi.org/10.1364/OE.19.010986 - 26. Aza, P.N., Fernandez-Pradas, J.M. and Serra, P. (2003) In Vitro Bioactivity of Laser Ablation Pseudowollastonite Coating. Biomaterials, 25, 1983-1990.
http://dx.doi.org/10.1016/j.biomaterials.2003.08.036
Nomenclature
NOTES
*Corresponding author.












