Materials Sciences and Applications
Vol.5 No.2(2014), Article ID:43186,8 pages DOI:10.4236/msa.2014.52011
Investigation of Self-Diffusion and Structure in Calcium Aluminosilicate Slags by Molecular Dynamics Simulation
![]()
1Department of Energy and Resources Engineering, College of Engineering, Peking University, Beijing, China; 2Beijing Building Materials Academy of Sciences Research, Beijing, China.
Email: *zuotaizhang@coe.pku.edu.cn
Copyright © 2014 Kai Zheng et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Kai Zheng et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 27th, 2013; revised December 30th, 2013; accepted January 11th, 2014
KEYWORDS
Molecular Dynamics; Self-Diffusion; Degree of Polymerization; Structural Defects; Al2O3/SiO2 Ratio
ABSTRACT
Molecular dynamics simulation is applied to investigate the mechanism and variation of self-diffusion in calcium aluminosilicate slags. The self-diffusion coefficients are calculated for eleven slag compositions with varying Al2O3/SiO2 ratios at a fixed CaO content. In practice, the results of the study are relevant to the significant changes in transport phenomenon caused by the changes in chemical composition during continuous casting of steels containing high amounts of dissolved aluminum. The cooperative movement between O atoms and network formers is discussed since [AlO4] and [SiO4] tetrahedra are the elementary structural units in the CaO-Al2O3-SiO2 (CAS) slag system. The diffusivities for four atomic types are affected by the degree of polymerization (DOP) of slag network characterized by the proportions of non-bridging oxygen (NBO) and Qn species in the system. On the other hand, a sudden increase in 5-coordinated Al as network modifiers in high alumina regions slightly increases the self-diffusion coefficient for Al. As another structural defect, oxygen tricluster plays an important role in the behavior of self-diffusion for O atoms, while the diffusivity for Ca is deeply influenced by its bonding and coordinating conditions.
1. Introduction
Silicate, aluminate and aluminosilicate melts are of great importance in both geology and industry because they are the most frequently used components of glasses, ceramics and molten slags. Among them, the calcium aluminosilicate (CAS) ternary system is especially attractive. For example, some CAS glasses are good candidates for the storage of nuclear waste and a wide range of other technical applications due to their outstanding mechanical and optical properties [1-3]. The slags composed of the ternary melts are also widely used in ironmaking and steelmaking processes [4]. Knowledge of physical and chemical properties of aluminosilicate liquids is fundamental for optimizing compositions and conditions for the production of particular glasses and slags. Since the macroscopic properties are determined by the system’s microscopic processes, it is important to acquire the atomic-scale structure and dynamics information, such as self-diffusivity, which has been studied through various sorts of techniques [5-13]. However, the changing regularity of self-diffusion coefficient with varying Al2O3/ SiO2 ratio at a constant CaO mole fraction has not been investigated so far.
The steels containing high amount of aluminum such as transformation-induced plasticity assisted steels (TRIP steels) are recently widely applied in lightweight automotive industry because of their high auxiticity and excellent deformability [14]. The SiO2 contained in the slags is expected to react with the additional Al in the steel and this reaction will increase the Al2O3/SiO2 ratio and cause considerable changes in structural and thermophysical properties of slags during the casting process. One such property is the viscosity of the molten slags which can be interpreted and predicted by self-diffusion constants of involved atoms. Therefore, understanding the mechanisms of self-diffusivity and its variation tendency with compositions in CAS slags is of crucial scientific and practical interest. In general, self-diffusivity is calculated by the mean square displacement (MSD), elucidated as the mobility of the cations and anions in a certain slag system where no chemical gradients exist [15] and are basically determined by the DOP [16]. DOP is further parameterized in accordance with the mean number of NBOs per tetrahedrally coordinated network-forming cation, or by the relative mole fraction of Qn species, where Qn refers to tetrahedral Si or Al groups with n numbers of bridging oxygens (BO) [17]. It is well known that the [SiO4] and [AlO4] tetrahedra in CAS system are the fundamental structural units, giving rise to the cooperative movement of Si, Al, and O atoms. In fact, structural defects such as oxygen triclusters [18,19], 5- coordinated Al [20,21] also occupy a considerable quantity and have deep influences on the self-diffusivity of Si, Al, and O. The mobility of Ca atom varies as the role of Ca in the 3-dimensional network shifts from network modifier to charge compensating for [AlO4] tetrahedra with the decreasing CaO/Al2O3 mole ratio, accompanied by the variation of coordination condition around Ca atoms. In this paper, MD (Molecular Dynamic) simulation is applied to the CAS slags at a fixed CaO content of 30% and various molar ratios between SiO2 (64% to 24%) and Al2O3 (6% to 46%) to promote understanding the cooperative mechanism of self-diffusivity of different atom species and the change of self-diffusion coefficients of four types of atoms with varying Al2O3/SiO2 ratios. These studies may provide some clues to the approach of controlling the slags used in casting steels containing high amount of aluminum.
2. Simulation Method
The MD simulations were performed on 11 slag samples with a fixed CaO concentration and varying Al2O3/SiO2 mole ratio which is a simplification of a mold slag that is currently under trial in the casting process of TRIP steels. For every sample about 4000 number of atoms were placed in a cubic box. The details of the simulated compositions are summarized in Table 1.
A simple interatomic potential function of the BornMayer-Higgins (BMH) type which has reproduced the major structural features of CAS melts and glasses [12, 22-24] was applied and given below:
 (1)
(1)
where the terms represent Coulomb interaction using the standard charge of each element and repulsive interaction,

Table 1. The composition of slag melts and density of model cubic box.
respectively. Here U(rij), qi, and rij denotes pair potential, net charges and the distance between atoms i and j. Listed in Table 2 are adjustable values of parameters Aij and Bij which have been proven successful in the simulation of aluminosilicate slags [23,25]. Coulomb interactions were taken into account by means of Ewald method and a cutoff distance of 10Å was used in evaluation of the repulsive forces.
Periodic boundary conditions were introduced to all faces of the simulating box to create an infinite system without boundaries. The leap frog integration method was applied to the simulation and the initial velocities were drawn randomly from a Maxwell-Boltzmann distribution. Before the simulation starts, the equilibrated slag samples at 5000 K have been obtained by both relaxing a random configuration for 30,000 time steps (the time for each step is 1 fs) and a Metropolis Monte Carlo method. Subsequently, the sample was cooled down from 5000 K to 2000 K in steps of 500 K in NVT ensemble and the total potential energy was relaxed for 20 ps between every two cooling steps. Then the temperature was fixed at 2000 K for another 30,000 time steps. Finally, the position coordinates at the end of the cooling runs were used as the initial conformation for the following simulation of 100,000 time steps at 2000 K. In this period the MSD was calculated and the microscopic structural information was collected to do further analysis.
3. Results and Discussion
3.1. Mean Square Displacement
MSD indicates the average displacement of a tagged
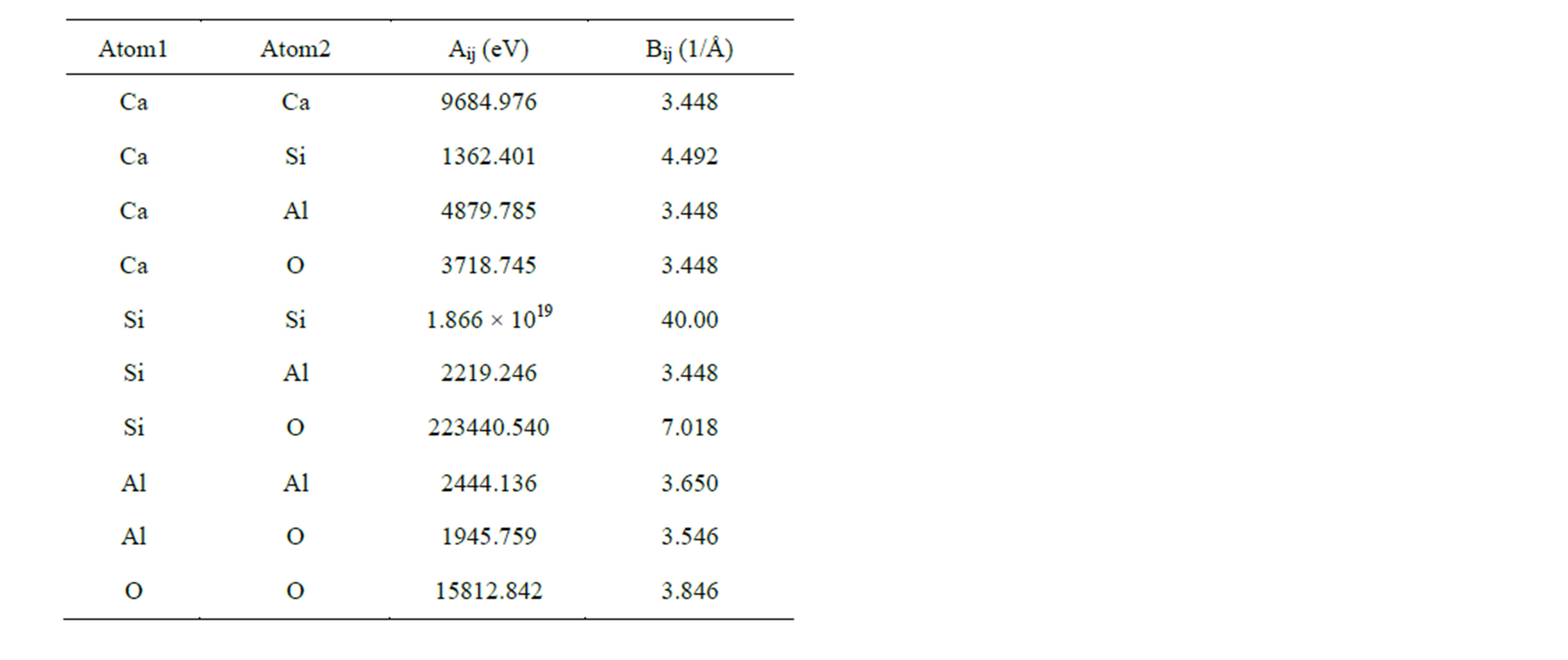
Table 2. Parameters for the BMH potentials.
atom during a fixed time t and was defined:
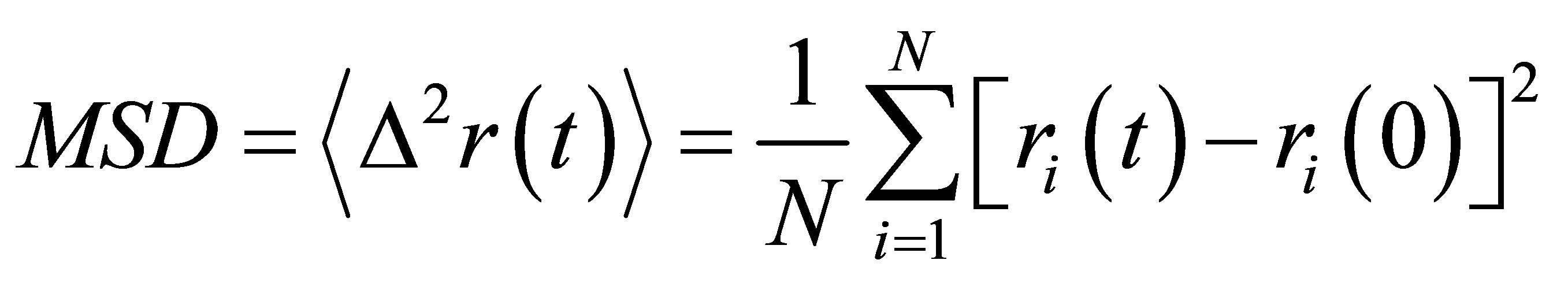 (2)
(2)
where ri(t) is the position of an atom at time t and the angular brackets imply an average over all the atoms. The MSD is given by summing the square of distance between the atom’s positions in different time steps and dividing by the number of atoms (N).
At each state point in the final 100,000 time steps, the MSD of a particular species is accumulated from the atom trajectories, and the variation of MSD depending on the simulating time is therefore acquired, as illustrated in Figure 1. Attention should be paid that the curves are plotted logarithmically for CAS7 with timescale shifting from femtosecond to 100 ps. Three different regimes with distinguishing features are identified for each atom, as many previous works have demonstrated [12,26]. At very short times (<1 ps) for all the 11 samples, atoms move on ballistic trajectories by virtue of the primary effect of inertia, which is reflected by MSD ~ t2 and recorded in Figure 1 for all atoms to 0.15 - 0.2 ps. Following the ballistic regime is the anomalous “subdiffusive” regime related to the plateau on curves. This phenomenon in atomic diffusion can be interpreted from a qualitative microscopic viewpoint by “cage effect” on oxygen that O atoms are provisionally confined to cages defined by O, T (Si or Al), and Ca sub-lattices for certain periods [12,26,27]. During this detention period, MSD barely changes with time because the oscillatory movement of trapped O atoms makes little contribution to its displacement. Furthermore, since the neighboring atoms making up the cages are themselves caged by surrounding atoms, plateaus are observed on other three curves with different time scale. According to Morgan and Spera’s works focusing on CaAl2Si2O8 glass [26], the ex-
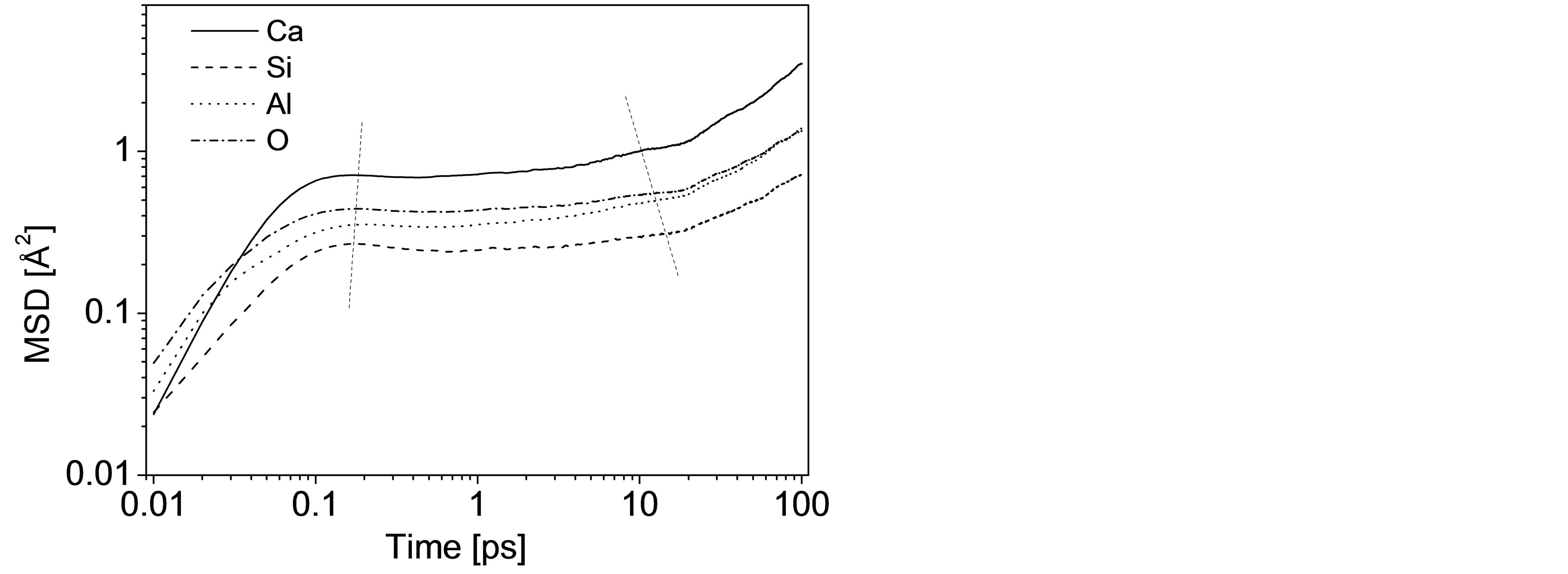
Figure 1. Logarithmic plot of the MSD vs. time at 2000 K illustrating the three different regimes.
tension of plateau is strongly temperature-depended and sub-diffusion becomes more pronounced at lower temperatures. For instance, the plateau doesn’t even appear after ballistic regime at ~5000 K, while the sub-diffusive regime dominates and extends out beyond 50 ps or exceeds the duration of the simulations at low temperatures. In our work the plateau of Ca maintains from 0.2 ps to 10 ps. Cooperative rearrangement of atoms is required for liberation of the imprisoned atom, and the diffusive regime is therefore attained. In this region Einstein random walk governs the atomic motion and the slope of the MSD is proportional to the self-diffusion coefficient (MSD ~ t, ΔMSD/Δt ~ D).
3.2. Self-Diffusion Coefficients
3.2.1. Cooperative Motion of Si, Al, and O
As one of the most crucial transport properties of molten slags, self-diffusion coefficient (D) of a tagged particle could be obtained from the MSD at long times by use of the Einstein’s equation:
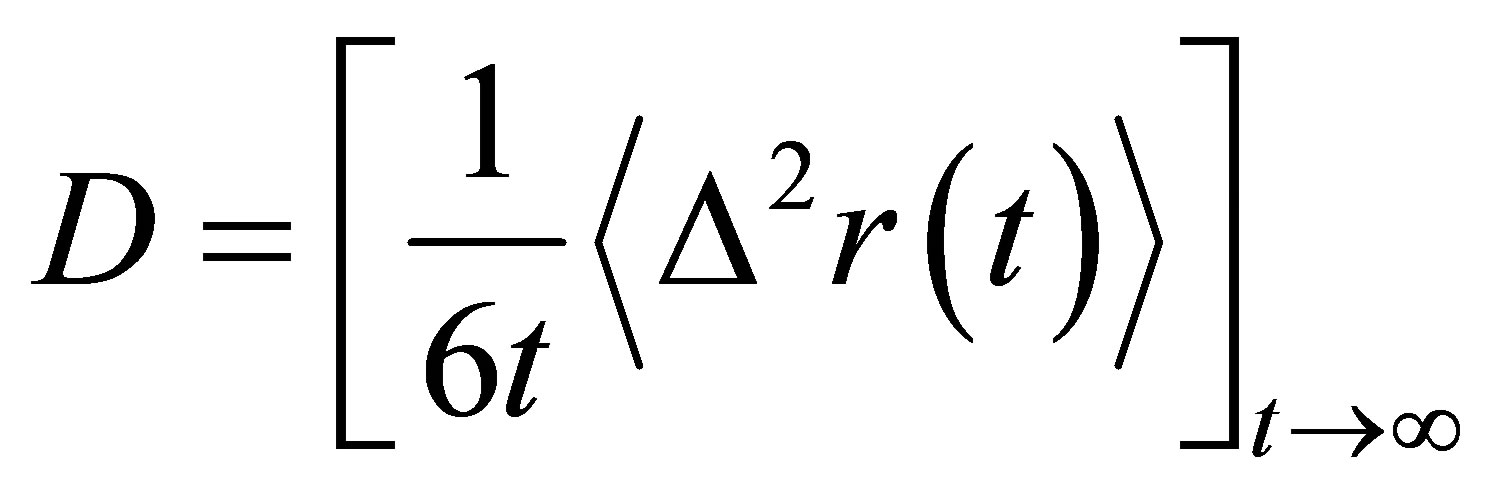 (3)
(3)
D is calculated from the slope of the MSD in the long-time diffusive regime defined earlier and Figure 2 shows the varying tendency of D for all atomic types as a function of Al2O3 mole fraction. DSi, DO basically decrease with Al2O3/SiO2 ratio, while DCa, DAl present slight increasing trends after decreasing with composition. For CaO-Al2O3-SiO2 slags at 1550˚C, resemblant experimental results stated that the viscosity first ascended and then descended with the increase of Al2O3/ SiO2 molar ratio [28]. The particular sequence of diffusivity for four atoms is Ca > Al > O > Si. Although it may seem quite strange at first sight to find a bigger self-diffusivity for Al than O, it is consistent with the experimental results by Liang et al using isotope tracer

Figure 2. Self-diffusion coefficients of Ca, Si, Al, O, and calculated value for O as a function of slag composition.
method [6] and simulated results by Tandia et al. [15], and also agrees well with the ordering of the elemental propensity by Vargheese and co-workers [27]. The activity of Ca always exceed others at all compositions for the obvious reason that Ca atoms are dispersed in the network composed by [SiO4] and [AlO4] tetrahedra and play the role of charge compensating or network modifier. Meanwhile, as the most stable structural unit in the slag, [SiO4] tetrahedra minimizes the diffusivity for Si.
It is noticed from Figure 2 that DAl, DSi, and DO share close values and a similar variation trend with the increasing Al2O3/SiO2 ratio. Special attention should be further laid on that DO is adjacent to DSi in the first four slags containing high silica, while it approximates with DAl when the mole fraction of Al2O3 dominates in last few samples. Consequently, the hypothesis can be made that [SiO4] and [AlO4] tetrahedra are the basic structural units in the process of diffusion and O atoms are moving cooperatively with Al and Si in those units. According to this assumption, DO for all 11 compositions could be calculated on the basis of diffusivities of Si and Al for the same slag sample with their mole fractions:
 (4)
(4)
where [Si]' and [Al]' are the relative concentration of Si and Al, calculated by
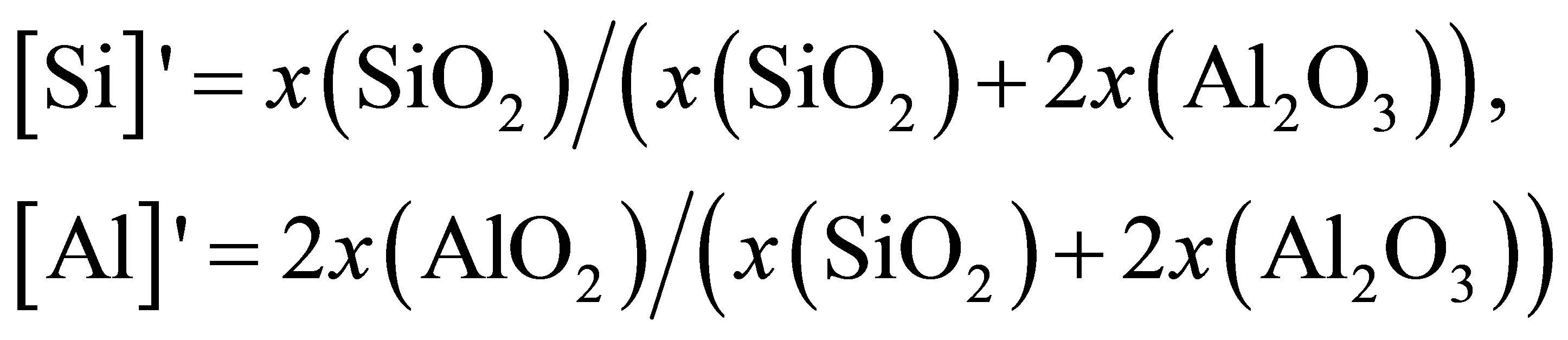
where x represents mole fraction. The calculated result is also presented in Figure 2 to compare with DO directly determined from simulation. The good agreement manifests that O atoms are moving together with Si or Al and the diffusivity of O is an average over O atoms in [SiO4] and [AlO4] units.
To reveal the structural mechanism of cooperative motion for Si, Al, and O, Radial distribution functions (RDF) of O-O atomic pair for CAS3, CAS8, and CAS11 are plotted in Figure 3(a), and there is an interesting transformation of the first peak for O-O pair. The first peak value equals to 2.62Å in the high silica region (CAS3), corresponding to the typical distance between oxygen atoms in a [SiO4] tetrahedron. While in an Al2O3 rich region (CAS11) the value converts to 2.84 Å, equal to the typical O-O distance in an [AlO4] tetrahedron. Similar result was reported by energy-dispersive x-ray diffraction experiments [29]. On the curve for CAS8, the peculiar peak accompanied by a distinct shoulder appears as the content of SiO2 and Al2O3 is approximately equivalent, as illustrated in Figure 3(b). The first peak of CAS8 is fitted with multi Gaussian peaks whose peak values equal to 2.60 Å and 2.86 Å, respectively. Since the O-O peaks in RDF provide the detailed information about what is the major structural unit in the network, it has been proven that the fundamental motion units in slags are [SiO4] and [AlO4] tetrahedra and O atoms move cooperatively with network formers.
3.2.2. Degree of Polymerization
DOP is a convenient parameter with which the nanoscale structures and macroscopic properties can be described and predicted. The variation of the diffusivity with composition is generally explained from several aspects,
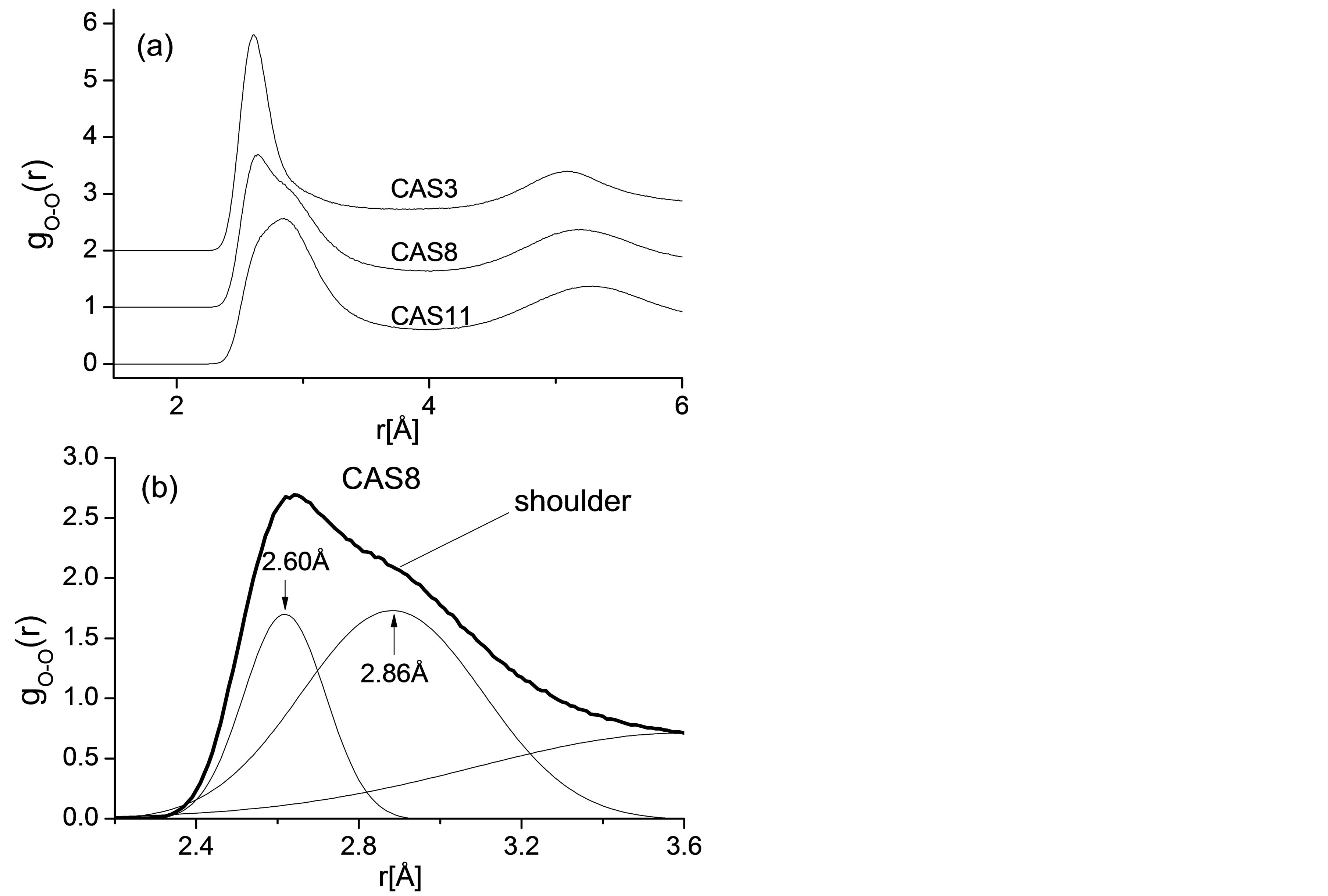
Figure 3. (a) RDFs for O-O pairs of all CAS3, CAS8 and CAS11; (b) Gaussian fitting result of the RDF’s first peak for O-O pair in CAS8.
and one of the most elementary and essential one is the DOP of the slag network, which is usually presented by number fraction of NBO and distribution of Qn species. Figure 4 shows the mole fraction of NBO varying with increasing Al2O3 concentration. The proportion of NBOs declines prominently from 28.5% to 5.9% with the substitution of Al2O3 for SiO2, which is identical with the traditional concept that the T-O-T linkages tend to be broken by Ca to form NBOs when the content of Ca exceeds that needed for charge balancing. However, NBOs still exist in the slags even when CaO/Al2O3 ratio is equal or less than 1 in CAS7 to CAS11, as previous works have demonstrated [30]. In our simulation DO decreases monotonously with increasing Al2O3/SiO2 ratio from 2.36 × 10−7 cm2·s−1 to 1.38 × 10−7 cm2·s−1, which is a little larger than the absolute measured values [6]. The decrease in diffusivity for O can be directly attributed to the reduction of NBOs, which leads to a rise in the number of rigid constraints on both oxygen and associated silicon. Despite the small fraction, NBOs are divided into two groups, namely Ca-Onb-Si and Ca-Onb-Al, and NBOs always prefer to be localized on Si to form Ca-Onb-Si according to 17O MAS NMR spectra [31], high-energy x-ray diffraction [32] and our simulation. Ca-Onb-Si is a weaker link compared with the bond Si-O-Si connected by a BO. Thus, DSi decreases with Al2O3/SiO2 ratio since the number of Ca-Onb-Si linkages declines owing to a decrease in the number of excess Ca atoms, except for the last two samples. Table 3 displays the proportions of Qn in [SiO4] and [AlO4] tetrahedral units for 11 CAS slags, and here n is the number of BO and oxygen tricluster in one tetrahedron. It is noted that the concentration of Q4 increases remarkably at the cost of the decreasing of Q2 and Q3, manifesting that the DOP increases with Al2O3/SiO2 ratio since it can be measured by (Q4 + Q3)/(Q2 + Q1). In this simulation the notable decrease in DCa and DAl in the region with CaO/Al2O3 > 1 (CAS1

Figure 4. Concentrations of NBO and oxygen tricluster versus mole fraction of Al2O3.
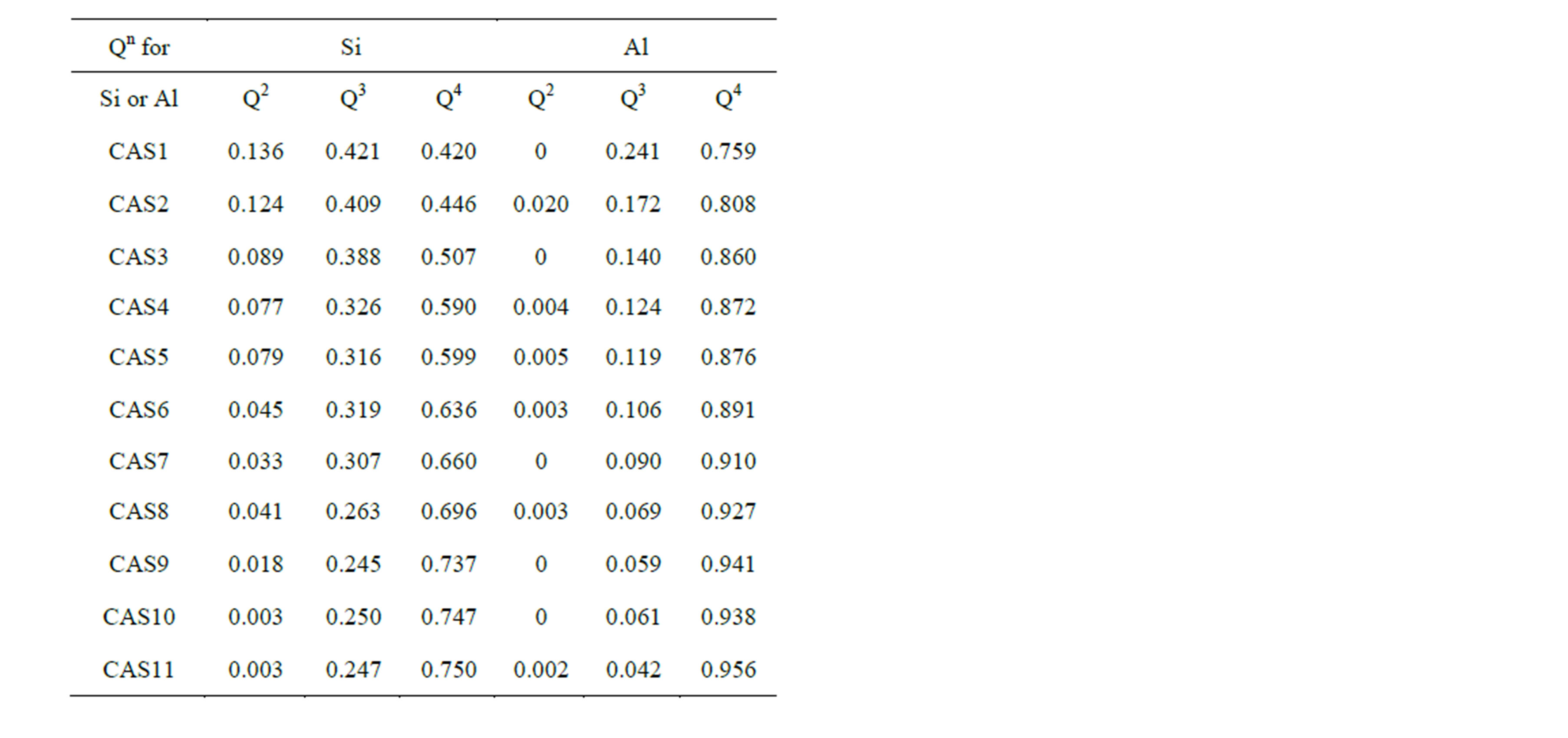
Table 3. Proportions of Qn for Si and Al in all 11 samples.
to CAS7) is basically caused by an increase of the network stability as a whole, and similar conclusion was obtained by other researchers [27].
3.2.3. Oxygen Triclusters and 5-Coodinated Al
Although the DOP of the slag network increases monotonously with a dramatic decline in the proportion of NBO, the diffusivities of the four atomic types exhibit anomalous changing regularity with composition, especially in the last few slag samples where CaO is insufficient to provide charge compensating for [AlO4] tetrahedra. It is shown in Figure 2 that DAl and DCa pass through shallow minimums in CAS8 and CAS7, respectively, while DO and DSi tend to remain invariable with composition in last four slags, suggesting that the selfdiffusion is also influenced by other factors. Oxygen triclusters (O atoms bonded with three network formers) and 5-coodinated Al have been widely investigated concentrating on their existence, conformation mechanism, quantities and effects on dynamics properties [20,23, 24,33]. They are often treated as the structural defects since O atoms are mostly linked with one or two network formers and Al are normally tetrahedrally coordinated with O, as stated in other literatures [15], these defects are likely to play a nonnegligible role in the diffusion process of CAS slags besides DOP. Number fractions of triclusters are traced and presented in Figure 4 with a prominent increase from 0.5% to 24% with the increase of Al2O3/SiO2 ratio. Oxygen triclusters in last four samples are generally comprised of O(Al, Al, Al) (more than 80% of all triclusters) with a small quantity of O(Al, Al, Si). For O(Al, Al, Al), the third network former cation being coordinated to Al-O-Al linkage slightly disturbs the charge arrangement around oxygen and elongates the length of Al-O bonds to 1.92 Å in average, compared with 1.77 Å for Al-BO. The increase in bond length will diminish the interatomic forces between O and Al. Hence DO barely decreases with increasing Al2O3/SiO2 ratio despite the increasing DOP when oxygen triclusters accumulate to a remarkable proportion of about 20% in CAS8 - CAS11. Figure 5 illustrates the distribution of Al with different coordination number as a function of Al2O3 mole fraction. AlIV preponderates over others with a percentage more than 87% and AlIII should be taken notice of especially in the first five CAS slags with the fraction of 4%. The concentration of AlV varies indistinctly with composition in the range between 4% and 10% and increases abruptly from 5.5% to 9.4% in CAS6 and CAS7. The abnormal variation for AlV can be interpreted by the amphoteric character of Al that the role of Al changes from an acid to an alkali with the substitution of Al for Si. When Ca is not enough to balance the negative charge of [AlO4], AlV together with oxygen triclusters will provide charge compensation for CAS systems [15,34]. This part of Al is supposed to turn to network modifiers from network formers, enhancing the diffusivity for AlV drastically. Therefore, a tender but significant increase of the diffusivity for Al in last four slag samples is observed as a result of the sudden increase in the concentration of AlV.
3.2.4. Bonding and Coordinating Conditions of Ca
The diffusivity of Ca reaches its minimum in CAS7 and possesses an increasing tendency afterwards. In general, Ca atoms associated with NBOs around Si atoms are less mobile than those playing a charge balancing role around Al atoms. In order to improve the comprehension of the exceptional variation in DCa, the bonding and coordinating conditions of Ca are probed into on a microscopic scale, including the bond length of Ca-O (rCa-O) and running coordination number (CN) of O around Ca with diverse compositions. Figure 6 elucidates the average bond length of Ca-O atomic pair and CNCa-O varying
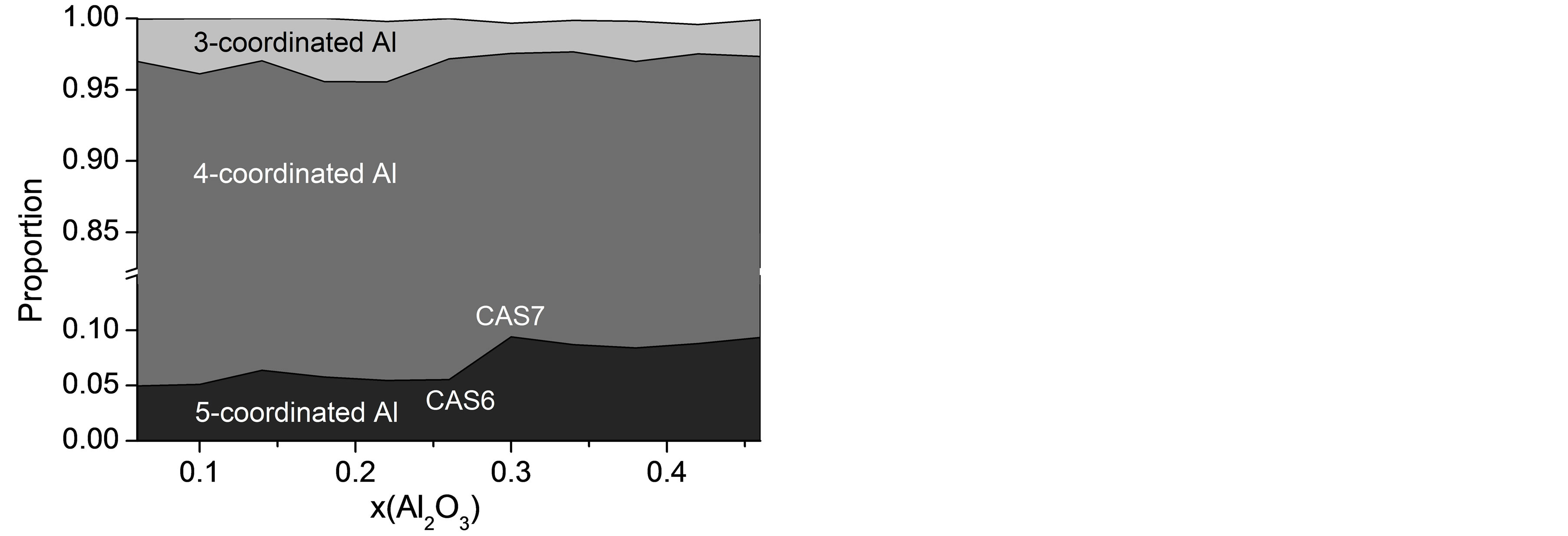
Figure 5. Proportions of Al coordinated with different numbers of O versus mole fraction of Al2O3.

Figure 6. Bond length and coordination number of Ca-O varying with mole fraction of Al2O3.
with Al2O3/SiO2 ratio. When [SiO4] units are gradually replaced by [AlO4], mean distance between Ca and O atoms increases from 2.33Å to 2.42Å and CNCa-O from 6.20 to 7.23, which is in accordance with others’ work [35,36]. On one hand, from the change in bond length we can see that the interatomic attraction between Ca and NBO in high silica regions is stronger than that between Ca and BO or tricluster when Ca atoms act as charge compensators. That is, Ca atoms may have a greater mobility in high alumina regions. On the other hand, an increase in CNCa-O implies more local constraints around Ca atoms and consequently a lower mobility. Therefore, the diffusivity for Ca is determined by the above two factors plus DOP of the slag network, and the proportion of their contributions to DCa differs with composition.
4. Conclusions
Molecular dynamics simulation was applied to CaO-SiO2- Al2O3 ternary slags with 11 different compositions to study the self-diffusion of the systems. Following results are obtained:
1) The curves of MSD for four types of atoms all reveal three different regimes with their own features, namely ballistic regime, sub-diffusive regime with a plateau and diffusive regime.
2) The sequence of diffusivity for four atoms is Ca > Al > O > Si. DAl, DSi, and DO share close values and similar variation trends with composition, indicating that O atoms move cooperatively with network-forming atoms in [SiO4] and [AlO4] tetrahedra.
3) DSi, DO approximately decrease with Al2O3/SiO2 ratio and DCa, DAl present minimums in CAS8 and CAS7, respectively. The decline in diffusivities can be mostly attributed to the decrease in DOP of the slag network.
4) A growing number of oxygen triclusters reduce the rate of descent in DO for last four slag samples, where 5-coordinated Al is considered to play the role of network modifier and result in a slight increase of the diffusivity for Al.
5) The variation of DCa is influenced by a combination of not only the DOP of networks but also the bonding and coordinating conditions around Ca atoms.
Acknowledgements
The authors gratefully acknowledge the financial support by the National Natural Science Foundation of China (51172003 and 51074009). Supports by the National High Technology Research and Development Program of China (863 Program, 2012AA06A114) and the China National Key Technology R & D Program (2011BAB03B02 and 2011BAB02B05) are also acknowledged.
REFERENCES
- D. R. Neuville, L. Cormier, B. Boizot and A.-M. Flank, “Structure of β-Irradiated Glasses Studied by X-Ray Absorption and Raman Spectroscopies,” Journal of NonCrystalline Solids, Vol. 323, No. 1-3, 2003, pp. 207-213. http://dx.doi.org/10.1016/S0022-3093(03)00308-9
- M. E. Lines, “Photoelastic Trends from Halides to Pnictides by a Bond-Orbital Method,” Journal of Applied Physics, Vol. 60, No. 4, 1986, pp. 1472-1478. http://dx.doi.org/10.1063/1.337274
- H. Hosono, K. Yamazaki and Y. Abe, “Reversible Optical Change of Amorphous Red Phosphorus in Reduced Phosphate Glasses,” Journal of the American Ceramic Society, Vol. 68, No. 1, 1985, pp. C304-C305. http://dx.doi.org/10.1111/j.1151-2916.1985.tb15242.x
- Z. T. Zhang, G. H. Wen, P. Tang and S. Sridhar, “The Influence of Al2O3/SiO2 Ratio on the Viscosity of Mold Fluxes,” ISIJ International, Vol. 48, No. 6, 2008, pp. 739- 746. http://dx.doi.org/10.2355/isijinternational.48.739
- P. B. Debenedetti and F. H. Stillinger, “Supercooled Liquids and the Glass Transition,” Nature, Vol. 410, No. 6825, 2001, pp. 259-267. http://dx.doi.org/10.1038/35065704
- Y. Liang, F. M. Richter, A. M. Davis and E. B. Watson, “Diffusion in Silicate Melts: I. Self Diffusion in CaOAl2O3-SiO2 at 1500˚C and 1 GPa,” Geochimica et Cosmochimica Acta, Vol. 60, No. 22, 1996, pp. 4353-4367. http://dx.doi.org/10.1016/S0016-7037(96)00288-8
- K. G. Ewsuk, S. J. Glass, R. E. Loehman, A. P. Tomsia and W. G. Fahrenholtz, “Microstructure and Properties of Al2O3-Al(Si) and Al2O3-Al(Si)-Si Composites Formed by in Situ Reaction of Al with Aluminosilicate Ceramics,” Metallurgical and Materials Transactions A, Vol. 27, No. 8, 1996, pp. 2122-2129. http://dx.doi.org/10.1007/BF02651867
- D. Nevins and F. J. Spera, “Molecular Dynamics Simulations of molten CaAl2Si2O8: Dependence of Structure and Properties on Pressure,” American Mineralogist, Vol. 83, No. 11-12, 1998, pp. 1220-1230.
- A. Whittington, P. Richet and F. Holtz, “Water and the Viscosity of Depolymerized Aluminosilicate Melts,” Geochimica et Cosmochimica Acta, Vol. 64, No. 21, 2000, pp. 3725-3736. http://dx.doi.org/10.1016/S0016-7037(00)00448-8
- G. Gruener, P. Odier, D. De Sousa Meneses, P. Florian and P. Richet, “Bulk and Local Dynamics in Glass-Forming Liquids: A Viscosity, Electrical Conductivity, and NMR Study of Aluminosilicate Melts,” Physical Review B, Vol. 64, No. 2, 2001, pp. 024206(1-5).
- V. V. Hoang, “Dynamical Heterogeneity and Diffusion in High-Density Al2O3·2SiO2 Melts,” Physica B, Vol. 400, No. 1-2, 2007, pp. 278-286. http://dx.doi.org/10.1016/j.physb.2007.07.023
- N. A. Morgan and F. J. Spera, “A Molecular Dynamics Study of the Glass Transition in Ca Al2Si2O8,” American Mineralogist, Vol. 86, No. 4, 2001, pp. 915-926.
- J. Horbach, W. Kob and K. Binder, “Molecular Dynamics Simulation of the Dynamics of Supercooled Silica,” Philosophical Magazine Part B, Vol. 77, No. 2, 1998, pp. 297-303. http://dx.doi.org/10.1080/13642819808204955
- B. Sauerhammer, M. Spiegel, D. Senk, E. Schmidt, S. Sridhar and M. Safi, “Effect of Liquid Phase on Scale Formation during High-Temperature Oxidation of AlSiTransformation-Induced Plasticity Steel Surfaces,” Metallurgical and Materials Transactions B, Vol. 36, No. 4, 2005, pp. 503-512.
- A. Tandia, N. T. Timofeev, J. C. Mauro and K. D. Vargheese, “Defect-Mediated Self-Diffusion in Calcium Aluminosilicate Glasses: A Molecular Modeling Study,” Journal of Non-Crystalline Solids, Vol. 357, No. 7, 2011, pp. 1780-1786. http://dx.doi.org/10.1080/13642819808204955
- B. T. Poe, P. F. McMillan, D. C. Rubie, S. Chakraborty, J. Yarger and J. Diefenbacher, “Silicon and Oxygen SelfDiffusivities in Silicate Liquids Measured to 15 Gigapascals and 2800 Kelvin,” Science, Vol. 276, No. 5316, 1997, pp. 1245-1248. http://dx.doi.org/10.1126/science.276.5316.1245
- S. K. Lee and J. F. Stebbins, “Disorder and the Extent of Polymerization in Calcium Silicate and Aluminosilicate Glasses: O-17 NMR Results and Quantum Chemical Molecular Orbital Calculations,” Geochimica et Cosmochimica Acta, Vol. 70, No. 16, 2006, pp. 4275-4286. http://dx.doi.org/10.1016/j.gca.2006.06.1550
- M. J. Toplis, D. B. Dingwell and T. Lenci, “Peraluminous Viscosity Maxima in Na2O-Al2O3-SiO2 Liquids: The Role of Triclusters in Tectosilicate melts,” Geochimica et Cosmochimica Acta, Vol. 61, No. 13, 1997, pp. 2605- 2612. http://dx.doi.org/10.1016/S0016-7037(97)00126-9
- J. F. Stebbins, J. V. Oglesby and S. Kroeker, “Oxygen Triclusters in Crystalline CaAl4O7 (Grossite) and in Calcium Aluminosilicate Glasses: 17O NMR,” American Mineralogist, Vol. 86, No. 3, 2001, pp. 1307-1311.
- D. R. Neuville, L. Cormier, V. Montouillout and D. Massiot, “Local Al Site Distribution in Aluminosilicate Glasses by 27Al MQMAS NMR,” Journal of Non-Crystalline Solids, Vol. 353, No. 2, 2007, pp. 180-184. http://dx.doi.org/10.1016/j.jnoncrysol.2006.09.035
- S. Sen and R. E. Youngman, “High-Resolution Multinuclear NMR Structural Study of Binary Aluminosilicate and Other Related Glasses,” The Journal of Physical Chemistry B, Vol. 108, No. 23, 2004, pp. 7557-7564. http://dx.doi.org/10.1021/jp031348u
- T. Matsumiya, A. Nogami and Y. Fukuda, “Applicability of Molecular Dynamics to Analyses of Refining Slags,” ISIJ International, Vol. 33, No. 1, 1993, pp. 210-217. http://dx.doi.org/10.2355/isijinternational.33.210
- P. Ganster, M. Benoit, W. Kob and J.-M. Delaye, “Structural Properties of a Calcium Aluminosilicate Glass from Molecular-Dynamics Simulations: A Finite Size Effects Study,” The Journal of Chemical Physics, Vol. 120, No. 21, 2004, pp. 10172-10181. http://dx.doi.org/10.1063/1.1724815
- F. J. Spera, D. Nevins, M. Ghiorso and I. Cutler, “Structure, Thermodynamic and Transport Properties of CaAl2Si2O8 Liquid. Part I: Molecular Dynamics Simulations,” Geochimica et Cosmochimica Acta, Vol. 73, No. 22, 2009, pp. 6918-6936. http://dx.doi.org/10.1016/j.gca.2009.08.011
- K. Zheng, Z. T. Zhang, F. H. Yang and S. Sridhar, “Molecular Dynamics Study of the Structural Properties of Calcium Aluminosilicate Slags with Varying Al2O3/SiO2 Ratios,” ISIJ International, Vol. 52, No. 3, 2012, pp. 342- 349.
- N. A. Morgan and F. J. Spera, “Glass Transition, Structural Relaxation, and Theories of Viscosity: A Molecular Dynamics Study of Amorphous CaAl2Si2O8,” Geochimica et Cosmochimica Acta, Vol. 65, No. 21, 2001, pp. 4019-4041. http://dx.doi.org/10.1016/j.gca.2009.08.011
- K. D. Vargheese, A. Tandia and J. C. Mauro, “Origin of Dynamical Heterogeneities in Calcium Aluminosilicate Liquids,” The Journal of Chemical Physics, Vol. 132, No. 19, 2010, pp. 194501(1-9).
- C. M. Scarfe and D. J. Cronin, “Viscosity-Temperature Relationships at I atm in the System Diopside-Anorthit,” American Mineralogist, Vol. 68, No. 11-12, 1983, pp. 1083-1088.
- V. Petkov, T. Gerber and B. Himmel, “Atomic ordeRing in Cax/2AlxSi1−xO2 Glasses (x =0, 0.34, 0.5, 0.68) by Energy-Dispersive x-Ray Diffraction,” Physical Review B, Vol. 58, No. 18, 1998, pp. 11982-11989. http://dx.doi.org/10.1103/PhysRevB.58.11982
- J. F. Stebbins and Z. Xu, “NMR Evidence for Excess Non-Bridging Oxygen in an Aluminosilicate Glass,” Nature, Vol. 390, No. 6655, 1997, pp. 60-62. http://dx.doi.org/10.1038/36312
- J. R. Allwardt, S. K. Lee and J. F. Stebbins, “Bonding Preferences of Non-Bridging Oxygens in Calcium Aluminosilicate Glass: Evidence from 17O MAS and 3QMAS NMR on Calcium Aluminate and Low-Silica Ca-Aluminosilicate Glasses,” American Mineralogist, Vol. 88, 2003, pp. 949-954.
- V. Petkov, S. J. L. Billinge, S. D. Shastri and B. Himmel, “Polyhedral Units and Network Connectivity in Calcium Aluminosilicate Glasses from High-Energy X-Ray Diffraction,” Physical Review Letters, Vol. 85, No. 16, 2000, pp. 3436-3439. http://dx.doi.org/10.1103/PhysRevLett.85.3436
- M. Schmucker and H. Schneider, “New Evidence for Tetrahedral Triclusters in Aluminosilicate Glasses,” Journal of Non-Crystalline Solids, Vol. 311, No. 2, 2002, pp. 211-215. http://dx.doi.org/10.1016/S0022-3093(02)01632-0
- D. R. Neuville, L. Cormier and D. Massiot, “Al coordination and Speciation in Calcium Aluminosilicate Glasses: Effects of Composition Determined by 27Al MQ-MAS NMR and Raman Spectroscopy,” Chemical Geology, Vol. 229, No. 1-3, 2006, pp. 173-185. http://dx.doi.org/10.1016/j.chemgeo.2006.01.019
- A. C. Hannon and J. M. Parker, “The Structure of Aluminate Glasses by Neutron Diffraction,” Journal of NonCrystalline Solids, Vol. 274, No. 1-3, 2000, pp. 102-109. http://dx.doi.org/10.1016/j.chemgeo.2006.01.019
- L. Cormier, D. Ghaleb, D. R. Neuville, J.-M. Delaye and G. Calas, “Chemical Dependence of Network Topology of Calcium Aluminosilicate Glasses: A Computer Simulation Study,” Journal of Non-Crystalline Solids, Vol. 332, No. 1-3, 2003, pp. 255-270. http://dx.doi.org/10.1016/j.jnoncrysol.2003.09.012
NOTES
*Corresponding author.

