Circuits and Systems
Vol.06 No.10(2015), Article ID:60834,13 pages
10.4236/cs.2015.610023
Current Mode Universal Filter Using Single Current Controlled Differential Difference Current Conveyor Transconductance Amplifier
Ajay Kumar Kushwaha, Sajal K. Paul*
Department of Electronics Engineering, Indian School of Mines, Dhanbad, India
Email: ajay.igecsagar@gmail.com, *sajalkpaul@rediffmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 August 2015; accepted 27 October 2015; published 30 October 2015
ABSTRACT
This research paper contains a new electronically tunable current-mode biquadratic universal filter using a new active building block; current controlled differential difference current conveyor transconductance amplifier (CCDDCCTA). The proposed filter provides the following important and desirable features: (i) One can use only one CCDDCCTA and two capacitors; (ii) One can get low pass (LP), band pass (BP), high pass (HP), notch (NF) and all pass (AP) current responses from the same configuration without any alteration; (iii) Passive components are grounded, which ease the integrated circuit implementation; (iv) Responses are electronically tunable; and (v) Sensitivity is low. Moreover, the non-ideality analysis shows that the parasitic passive components can be compensated for the proposed circuit. The functionality of the design is verified through SPICE simulations using 0.25 µm CMOS TSMC technology process parameters. Simulation result agrees well with the theoretical analysis.
Keywords:
Current Mode Analog Filter, Universal Filter, Current Controlled Differential Difference Current Conveyor Transconductance Amplifier (CCDDCCTA), Monte-Carlo Analysis

1. Introduction
Universal biquadratic filters are those which provide all standard filter functions (low pass (LP), band pass (BP), high pass (HP), notch (NF) and all pass (AP)), without modifying the circuit topology. The advancement in the field of microelectronics presents current mode active building blocks for design of fast and high performance analog signal processing circuits and systems [1] . The current mode active blocks may process signals in voltage as well as current mode. A number of current mode filters using various analog building blocks (ABB) are available in literature under the classification of multi-input multi-output (MIMO) [2] -[5] , single-input multi- output (SIMO) [6] -[11] and multi-input single-output (MISO) [12] - [24] . In addition, a range of current conveyor blocks with inbuilt transconductance amplifier (TA) in monolithic chip, such as current conveyor transconductance amplifier (CCTA) [25] , current difference transconductance amplifier (CDTA) [26] , current controlled current conveyor transconductance amplifier (CCCCTA) [27] , differential voltage current conveyor transconductance amplifier (DVCCTA) [19] , differential difference current conveyor transconductance amplifier (DDCCTA) [4] , differential voltage current controlled conveyor transconductance amplifier (DVCCCTA) [28] and current controlled differential difference current conveyor transconductance amplifier (CCDDCCTA) [29] , have emerged in last few years. Among these, CCDDCCTA is a recently introduced ABB. It is basically composed of current controlled differential difference current conveyor (CCDDCC) [30] followed by a transconductance amplifier (TA) block. It has high input impedance terminals for voltage and high output impedance terminals for currents. It can process both differential and floating inputs. It inherits all the good properties of CCDDCC, CCCCTA and DDCCTA along with electronic tuning of transconductance, which is found to be useful in design of various circuits with lesser number of resistors and integrated circuit implementation.
The study of MISO universal filters [13] - [24] based on current mode ABB reveals that these circuits suffer one or more of the following weakness:
(a) Use of two or more ABBs [13] - [16] [18] [20] - [24] ;
(b) Excessive use of the passive components [15] - [17] [19] [21] ;
(c) No grounded passive components [15] [16] ;
(d) Requirement of four or more input current signal to get all the responses [15] - [18] ;
(e) Requirement of gain of input signal such as 2Iin or 3Iin [13] - [15] [20] [23] [24] ;
(f) Lack of electronic tunability [15] [16] ;
(g) Non-orthogonality of pole frequency and quality factor [13] - [15] [20] - [22] [24] .
A new current mode universal filter with a reduced number of passive components has been presented. The proposed filter is a multi-input single-output (MISO) and uses two grounded capacitors and one CCDDCCTA only. The proposed current mode filter circuit can realize high pass (HP), low pass (LP), band pass (BP), notch and all pass (AP) filter responses by selecting appropriate input current without alteration of the topology. It can easily be cascaded, as its output is current and impedance is high. All the features of the proposed filter can be electronically adjusted by biasing currents of the CCDDCCTA. Moreover, the high-Q filter may easily be achieved by using the bias currents of CCDDCCTA. A comparative study of the available active elements based on current mode filters is also presented. PSPICE simulation results verify the theoretical analysis.
2. Circuit Description
The symbol of CCDDCCTA and its implementation using CMOS are shown in Figure 1 and Figure 2 respectively.
Figure 1. Symbol of CCDDCCTA.
Figure 2. Implementation of CCDDCCTA using CMOS.
The port relationships of the CCDDCCTA can be represented by the following matrix:
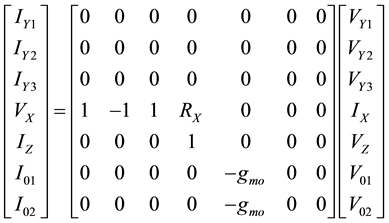 (1)
(1)
where, the intrinsic resistance
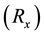 at X terminal defined as
at X terminal defined as
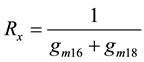 (2)
(2)
where,
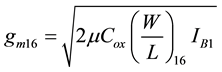 (3)
(3)
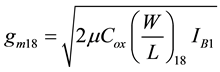 (4)
(4)
Similarly, the transconductance
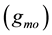 from Z terminal to O terminal may be expressed as
from Z terminal to O terminal may be expressed as
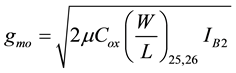 (5)
(5)
It may be noted that both
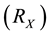 and
and
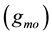 can be electronically varied by bias currents IB1 and IB2 of CCDDCCTA respectively.
can be electronically varied by bias currents IB1 and IB2 of CCDDCCTA respectively.
The proposed current mode (CM) filter is shown in Figure 3 which utilizes two grounded capacitors and one CCDDCCTA only. The routine analysis of circuit gives the output current at single node as:
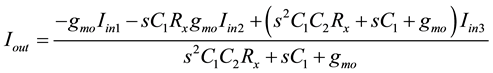 (6)
(6)
The inspection of Equation (6) reveals that the circuit of Figure 3 will function as a universal filter depending upon combination of inputs (Iin1, Iin2 and Iin3) applied at three terminals. The output response (Iout) for different combinations of inputs are shown in Table 1. It reveals that no component constraint is required for LP and BP response; however for HP, notch and AP responses a simple component matching is required. The circuit is suitable for cascading to another circuit having low input impedance for current input.
The filter parameters, namely natural angular frequency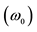 , bandwidth (BW) and quality factor
, bandwidth (BW) and quality factor
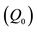 are obtained respectively as
are obtained respectively as
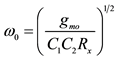 ,
,
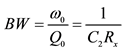 , and
, and

It reveals in Table 1 and (7) that for LP and BP responses

















The sensitivity of a parameter Y to variation of element X may be defined as

The sensitivity analysis of the proposed circuits for various parameters is evaluated as


Figure 3. Proposed current mode universal filter.
Table 1. The Iin1, Iin2 and Iin3 values selection for each filter function response.



It reveals that the sensitivity is low and less then unity in magnitude.
3. Non-Idealities Analysis
The performance of the proposed current mode filter might be deviated from the ideal response due to non- idealities of CCDDCCTA. The first non-ideality comes due to the internal current (α) and voltage (β) transfer of CCDDCCTA and hence modified port relationships with current and voltage transfer non-ideality can be expressed in matrix form as

where, voltage tracking error coefficient





The filter parameters can be expressed as



It is noticed that the non-idealities affect the parameters of the filter. The sensitivity analysis of










It reveals that with non-ideality; the sensitivity is still low and magnitude is within unity.
The second non-ideality comes due to the parasites of CCDDCCTA comprising of capacitances and resistances connected in parallel at Z, O and Y terminals. The effect of these parasites is very much dependent on the circuit topology. The current mode universal filter with non-ideality is shown in Figure 4. The modified capacitances are






4. Simulation Result and Discussion
The current mode universal filter as proposed in Figure 3 is simulated with PSPICE. The 0.25 µm CMOS TSMC technology process parameters are used for simulation. The aspect ratio of various transistors is stated in Table 2. The supply voltages of ±1.25 V and VBB = −0.8 V are used. To design the filter for a pole frequency of


To test the orthogonal variation of






It is well known that a little tolerance of the value of the various components occurs during manufacturing and even afterword resulting in deviation of various parameters of filters such as central frequency, quality factor and bandwidth from its designed values. The collection of statistical data due to tolerance of passive components is obtained using Monte-Carlo analysis for band pass filter. As an example, for a 100 pF ± 5% capacitor, the actual measured capacitor value to be somewhere between 95 pF and 105 pF. Monte-Carlo runs to cover as
Figure 4. Current mode universal filter with non-ideality.
Table 2. Aspect ratio of various transistors.
Figure 5. Simulated and theoretical response for low pass filter.
Figure 6. Simulated and theoretical response for high pass filter.
Figure 7. Simulated and theoretical response for band pass filter.
Figure 8. Simulated and theoretical response for notch filter.
Figure 9. Simulated and theoretical gain and phase response for all pass filter.
Figure 10. Variation of pole frequency (

Table 3. Bias current values for orthogonal adjustment of


Table 4. Bias current values for orthogonal adjustment of


Figure 11. Variation of quality factor (

many possible values of the component within their tolerance limits. It is performed by taking 5% Gaussian deviation of C1 and C2 values for 200 simulation runs for a pole frequency of 1.28 MHz. The result of Monte- Carlo simulation is shown in Figure 12 and corresponding histogram in Figure 13. As per statistical results as shown in Figure 13, the minimum and maximum frequency obtained are 1.18 MHz and 1.38 MHz respectively and standard deviation is 42.2 KHz. It reveals that the proposed filter exhibits a reasonable sensitivity performance. The quality of the output response may be judged with the help of percentage total harmonic distortion (%THD). The %THD of the output response for band pass filter with respect to the input is shown in Figure 14. It is found that the %THD is well within the tolerance range of 5%.
Comparative study of different available implementation of current mode MISO universal filters is given in Table 5. It is evident that most of the circuits suffers from one or more weakness in comparison to the proposed one. However circuits proposed in [17] [19] uses one active building block as that of the proposed one. The circuit of [17] uses excessive number of passive components and is comparable to the proposed one.
Figure 12. Monte-Carlo 200 simulation runs for BP filter.
Figure 13. Monte-Carlo histogram for the BP filter.
Figure 14. Variation of %THD for band pass output response Vs input signal.
Table 5. Comparative study of the available active element based current mode MISO universal filter.
5. Conclusion
Current mode universal filter using current controlled differential difference current conveyor transconductance amplifier (CCDDCCTA) has been presented that uses two grounded capacitors and one CCDDCCTA only. It can realize high pass, low pass, band pass, notch and all pass responses from the same topology. The filter parameter can be electronically adjustable by bias currents IB1 and IB2. Table 5 shows the comparative study of the available current mode building block based MISO filters. PSPICE simulation results authenticate the theoretical results.
Cite this paper
Ajay KumarKushwaha,Sajal K.Paul, (2015) Current Mode Universal Filter Using Single Current Controlled Differential Difference Current Conveyor Transconductance Amplifier. Circuits and Systems,06,224-236. doi: 10.4236/cs.2015.610023
References
- 1. Ferri, G. and Guerrini, N.C. (2000) Low-Voltage Low-Power CMOS Current Conveyors. Kluwer Academic Publishers, Dordrecht, Netherlands.
- 2. Siripruchyanun, M. and Jaikla, W. (2008) CMOS Current Controlled Current Differencing Transconductance Amplifier and Applications to Analog Signal Processing. International Journal of Electronics and Communications, 62, 277-287.
http://dx.doi.org/10.1016/j.aeue.2007.05.001 - 3. Siripruchyanun, M. and Jaikla, W. (2008) Electronically Controllable Current Mode Universal Biquad Filter Using Single DO-CCCDTA. Circuits, Systems, and Signal Processing, 27, 113-122.
http://dx.doi.org/10.1007/s00034-008-9014-2 - 4. Pandey, N. and Paul, S.K. (2011) Differential Difference Current Conveyor Transconductance Amplifier (DDCCTA): A New Analog Building Block for Signal Processing. Journal of Electrical and Computer Engineering, 2011, Article ID: 361384.
- 5. Chen, H.P. (2012) Tunable Versatile Current Mode Universal Filter Based on Plus-Type DVCCs. International Journal of Electronics and Communications, 66, 332-339.
http://dx.doi.org/10.1016/j.aeue.2011.08.010 - 6. Prasad, D., Bhaskar, D.R. and Singh, A.K. (2009) Universal Current Mode Biquad Filter Using Dual Output Current Differencing Transconductance Amplifier. International Journal of Electronics and Communications, 63, 497-501.
http://dx.doi.org/10.1016/j.aeue.2008.02.012 - 7. Mangkalakeeree, S., Duangmalai, D. and Siripruchyanun, M. (2009) Current Mode KHN Filter Using Single CCCCTA. The Seventh PSU Engineering Conference, 21-22 May 2009, Songkla, Thailand, 306-309.
http://www.te.kmutnb.ac.th/~msn/khncctapec7.pdf - 8. Wanga, C., Xua, J., Keskinb, A.ü., Dua, S. and Zhanga, Q. (2011) A New Current Mode Current Controlled SIMO-Type Universal Filter. International Journal of Electronics and Communications, 65, 231-234.
http://dx.doi.org/10.1016/j.aeue.2010.02.010 - 9. Tangsrirat, W. (2011) Single Input Three-Output Electronically Tunable Universal Current Mode Filter Using Current Follower Transconductance Amplifiers. International Journal of Electronics and Communications, 65, 783-787.
http://dx.doi.org/10.1016/j.aeue.2011.01.002 - 10. Pandey, N., Nand, D. and Khan, Z. (2013) Single Input Four-Output Current Mode Filter Using Operational Floating Current Conveyor. Active and Passive Electronic Components, 2013, Article ID: 318560.
- 11. Prasad, D., Bhaskar, D.R. and Srivastava, M. (2013) Universal Current Mode Biquad Filter Using a VDTA. Circuits and Systems, 4, 29-33.
http://dx.doi.org/10.4236/cs.2013.41006 - 12. Siripruchyanun, M. and Jaikla, W. (2007) Current Controlled Current Conveyor Transconductance Amplifier (CCCCTA): A Building Block for Analog Signal Processing. In: Proceedings of the International Symposium on Communications and Information Technologies, IEEE Computer Society Press, Sydney, 209-211.
http://dx.doi.org/10.1109/iscit.2007.4392014 - 13. Tangsrirat, W., Dumawipata, T. and Surakampontorn, W. (2007) Multiple Input Single Output Current Mode Multifunction Filter Using Current Differencing Transconductance Amplifiers. International Journal of Electronics and Communication, 61, 209-214.
http://dx.doi.org/10.1016/j.aeue.2006.04.004 - 14. Lee, C.N. (2010) Multiple Mode OTA-C Universal Biquad Filters. Circuits, Systems & Signal Processing, 29, 263-274.
http://dx.doi.org/10.1007/s00034-009-9145-0 - 15. Horng, J.W. (2011) High Output Impedance Current-Mode Universal Biquadratic Filters with Five Inputs Using Multi-Output CCIIS. Microelectronics Journal, 62, 693-700.
http://dx.doi.org/10.1016/j.mejo.2011.02.007 - 16. Horng, J.W. (2011) Current-Mode Universal Biquadratic Filter with Five Inputs and One Output Using Tree ICCIIs. Indian Journal of Pure & Applied Physics, 49, 214-217.
http://nopr.niscair.res.in/bitstream/123456789/11155/1/IJPAP%2049(3)%20214-217.pdf - 17. Senani, R., Abdalla, K.K. and Bhaskar, D.R. (2011) A State Variable Method for the Realization of Universal Current-Mode Biquads. Circuits and Systems, 2, 286-292.
http://dx.doi.org/10.4236/cs.2011.24040 - 18. Channumsin, O., Pukkalanun, T. and Tangsrirat, W. (2011) Universal Current-Mode Biquad with Minimum Components. Proceedings of the International Multi Conference of Engineering and Computer Scientists, Hong Kong, 16-18 March 2011, 1012-1015.
http://www.iaeng.org/publication/IMECS2011/IMECS2011_pp1012-1015.pdf - 19. Pandey, N. and Paul, S.K. (2011) VM and CM Universal Filters Based On Single DVCCTA. Active and Passive Electronic Components, 2011, Article ID: 929507.
http://dx.doi.org/10.1155/2011/929507 - 20. Kumngern, M. (2011) Multiple-Input Single-Output Current-Mode Universal Filter Using Translinear Current Conveyors. Journal of Electrical and Electronics Engineering Research, 3, 162-170.
http://dx.doi.org/10.5897/jeeer11.023 - 21. Tangsrirat, W. and Pukkalanun, T. (2011) Structural Generation of Two Integrator Loop Filters Using CDTA and Grounded Capacitors. International Journal of Circuit Theory and Applications, 39, 31-45.
http://dx.doi.org/10.1002/cta.616 - 22. Jaikla, W., Siripongdee, S. and Suwanjanmiso, P. (2012) MISO Current-Mode Biquad Filter with Independent Control of Pole Frequency and Quality Factor. Radioengineering, 21, 886-891.
http://www.radioeng.cz/fulltexts/2012/12_03_0886_0891.pdf - 23. Satansup, J., Pukkalanun, T. and Tangsrirat, W. (2013) Electronically Tunable Current-Mode Universal Filter Using VDTAs and Grounded Capacitors. Proceedings of the International Multi Conference of Engineers and Computer Scientists, Hong Kong, 13-15 March 2013, 2.
http://www.iaeng.org/publication/IMECS2013/IMECS2013_pp647-650.pdf - 24. Srisakultiew, S., Lawanwisut, S. and Siripruchyanun, M. (2013) A Current-Mode Electronically Controllable Multi-function Biquadratic Filter Using CCCIIs. International Journal of Advances in Telecommunications, Electrotechnics, Signals and Systems, 2, 45-50.
http://dx.doi.org/10.11601/ijates.v2i1.11 - 25. Jaikla, W., Silapan, P., Chanapromma, C. and Siripruchyanun, M. (2008) Practical Implementation of CCTA Based on Commercial CCII and OTA. Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems, Bangkok, 8-11 December 2008, 1-4.
http://dx.doi.org/10.1109/ispacs.2009.4806670 - 26. Biolek, D. (2003) CDTA-Building Block for Current-Mode Analog Signal Processing. Proceedings of the European Conference on Circuit Theory and Design, Cracow, 1-4 September 2003, 397-400.
http://user.unob.cz/biolek/veda/articles/ECCTD03_2.pdf - 27. Siripruchyanun, M. and Jaikla, W. (2008) Current Controlled Current Conveyor Transconductance Amplifier (CCCCTA): A Building Block for Analog Signal Processing. Electrical Engineering, 90, 443-453.
http://dx.doi.org/10.1007/s00202-007-0095-x - 28. Maiti, S. and Pal, R.R. (2013) Universal Biquadratic Filter Employing Single Differential Voltage Current Controlled Conveyor Transconductance Amplifier. Lecture Notes on Photonics and Optoelectronics, 1, 56-61.
http://dx.doi.org/10.12720/lnpo.1.2.56-61 - 29. Pandey, N., Kumar, P. and Choudhary, J. (2013) Current Controlled Differential Difference Current Conveyor Transconductance Amplifier and Its Application as Wave Active Filter, ISRN Electronics, 2013, 1-11.
http://dx.doi.org/10.1155/2013/968749 - 30. Prommee, P. and Somdunyakanok, M. (2011) CMOS-Based Current Controlled DDCC and Its Applications to Capacitance Multiplier and Universal Filter. International Journal of Electronics and Communications, 65, 1-8.
http://dx.doi.org/10.1016/j.aeue.2009.12.002 - 31. Liu, S.L. (1995) High Input Impedance Filters with Low Component Spread Using Current Feedback Amplifier. Electronics Letter, 31, 1042-1043.
http://dx.doi.org/10.1049/el:19950725
NOTES
*Corresponding author.

















