Circuits and Systems
Vol.06 No.12(2015), Article ID:62409,12 pages
10.4236/cs.2015.612028
An 8 Bit 0.8 GS/s 8.352 mW Modified Successive Approximation Register Based Analog to Digital Converter in 65 nm CMOS
Ananthanarayanan Parthasarathy
Department of Electrical Engineering, Stanford University, Stanford, USA

Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 July 2015; accepted 27 December 2015; published 30 December 2015
ABSTRACT
We propose a new approach in reducing the power consumption of the successive approximation register Analog to Digital Converter (SAR-ADC) by changing the convergence algorithm of the Digital to Analog converter (DAC) input of the SAR-ADC. Different search algorithms such as binary search tree, moving binary search tree (BST), least significant bit shifter (LSB), adaptive algorithm and split-register moving BST algorithm are designed and analyzed for faster convergence of the DAC input. In this paper, we design a 0.8 GS/s, 8 bit (Effective number of bits (ENOB)―7.42), 8.352 mW SAR ADC with a proposed moving BST algorithm in 65 nm CMOS which ranks amongst the current state of the art ADCs with a FOM 65.25 fJ/step.
Keywords:
Moving Binary Search Tree, SAR-ADC, Low Power

1. Introduction
Analog to digital converters (ADC) are among the most important electronic structures due to the technological shift and advances in digital electronics. There are many tradeoffs in designing ADCs including power, cost, sampling speed, resolution; the most challenges are in designing a high frequency and low power ADC. In some applications, the size of device becomes the main concern; an example would be for imaging sensors that require an ADC for each pixel of input. Successive approximation register (SAR) analog-to digital converters (ADCs) require several comparison cycles to complete one conversion, and therefore have limited operational speed [1] [2] . SAR architectures are extensively used in low-power and low-speed (below several MS/s) applications. In recent years, with the feature sizes of CMOS devices scaled down, SAR ADCs have achieved several tens of MS/s to low GS/s sampling rates with 5-bit to 10-bit resolutions. To judge the performance of an ADC this parameter has been defined to consider everything in one unique parameter. This parameter is the main characteristic that monitors the quality of ADC.
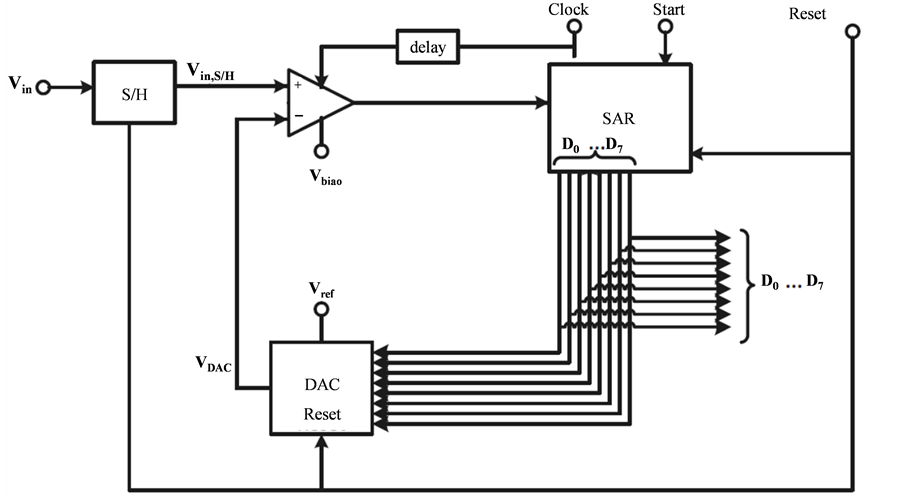
The good thing about this parameter is that it is not dependent on the structure [3] . This metric calculates the raw energy efficiency of ADC using equation [1] . The benefits of this equation are that it can be quickly calculated from a few ADC parameters and applied to assess the relative performance across different design approaches. The pioneers in designing ADC have considered remodeling the different state of the art components like the comparator, S/H circuit and DAC (Figure 1) to reduce the power consumption.
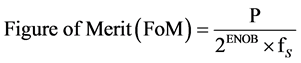 (1)
(1)
Here in this paper, we looked at a different idea of reducing the power consumption by decreasing the iterations and the time it takes for the DAC to stabilize to its input value. We propose different search algorithms for SAR-ADC and analyze the design and performance tradeoffs. We feel that this could potentially be used to design low power consumption ADCs.
Most commonly [4] , binary search algorithm is used for DAC input convergence since it is fastest search algorithm existing for finding a value in a random group of arranged numbers with O (logn) as its Big O notation. Though this might not be suitable if the input signal is slowly varying or if the values are within a range (like audio signals) then we can come up with algorithms that can converge faster to the required value. In all our cases in this paper, we are assuming the number of bits to be 10 (0 to 1023) for explaining the proof of concept.
2. Binary Search Tree Algorithm
The regular binary search tree (Figure 2) always starts with the middle value 1000000000 (i.e. 512) and compares with the actual input. If the output of the comparator (Cp) happens to be 1, then it means that the value lies between 512 and 1053; and if it is 0, then the value lies between 0 and 512. If Cp equals 1, then the value is readjusted to 768 and the comparison is done again. This is repeated until the value equals the input value to the comparator. One of the biggest disadvantages is that, the BST always starts comparing from the center value even if the signal is close to the boundary conditions; also if the current value is very close to the previous value, then the number of comparisons done to reach the actual target is higher than the difference between the two numbers.
Figure 1. Typical block diagram of SAR-ADC.
Figure 2. A general binary search tree.
The following example illustrates the mechanism of the circuits. For instance, the two consecutive digital signals, D, are:
D [10] = 1001100001 (current signal―609).
D [10] = 1001100010 (previous signal―610).
The number of conversions for the binary search to reach to the value of 609 is 9.
(10000000000 -> 1100000000 -> 1010000000 -> 1001000000 -> 1001100000 -> 1001110000 -> 1001101000 -> 1001100100 -> 1001100010 -> 1001100001)
Irrespective of what the previous signal is, the binary search always starts from the middle value 1000000000 (512). This happens to be a concern because if we come up with algorithms that take this into consideration, then much power can be saved.
3. Moving Binary Search Tree Algorithm
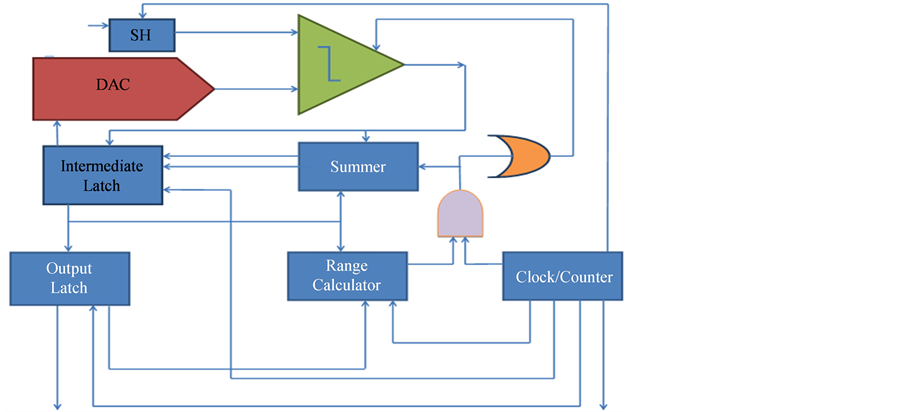
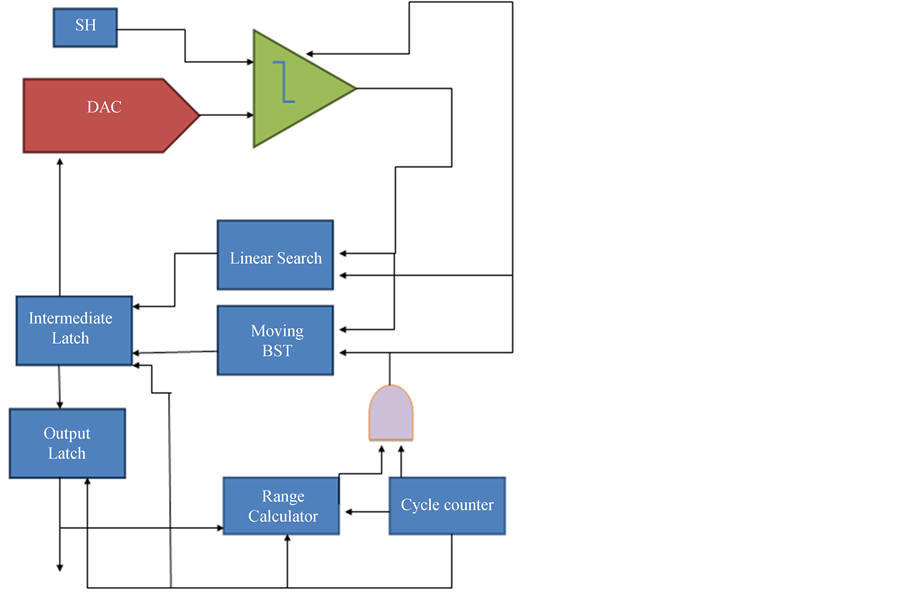
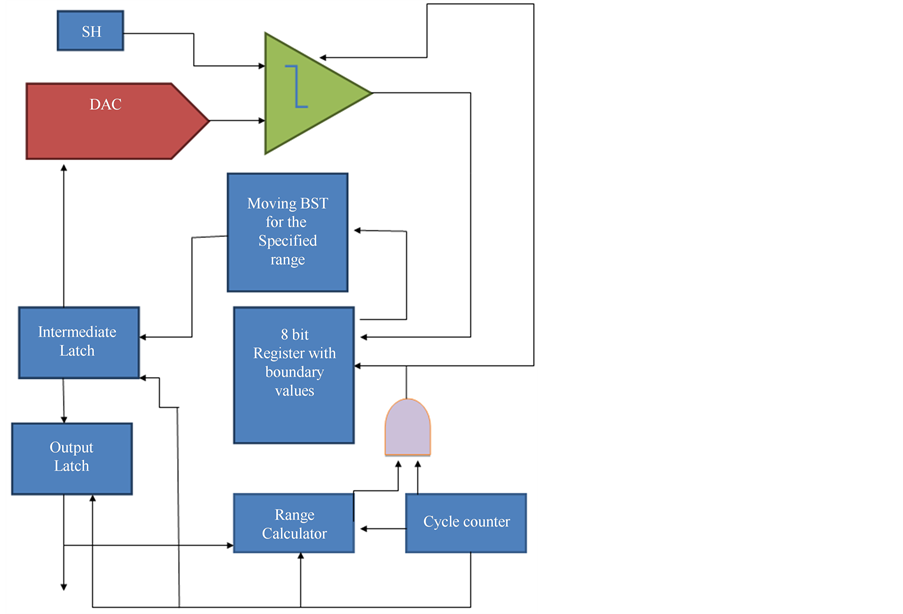
In order to overcome the limitation of BST, we have proposed moving BST. The moving binary search tree starts with the previous value and compares with the actual input. If the output of the comparator (Cp) happens to be 1, then it means that the value lies between previous value and 1053; and if it is 0, then the value lies between 0 and previous value. If Cp equals 1, then the value is readjusted to (previous value + 1053/2) and the comparison is done again. This is repeated until the value equals the input value to the comparator. How can this method be better than the regular binary search tree? The number of iterations it takes for the regular binary search tree to converge to the current value is higher than the moving binary search tree because the span or the range in which the moving binary search tree searches is lower. A moving BST can be implemented using the control structure in Figure 3.
The following example illustrates the mechanism of the circuits. For instance, the two consecutive signals are:
D [10] = 1001100001 (current signal―609).
D [10] = 1001011111 (previous signal―607).
The number of conversions for the moving binary search to reach to the value of 609 is 7.
(1001011111 -> 1101011111 -> 1011011111 -> 1001111111 -> 1001101111 -> 1001100111 -> 1001100011 -> 1001100001)
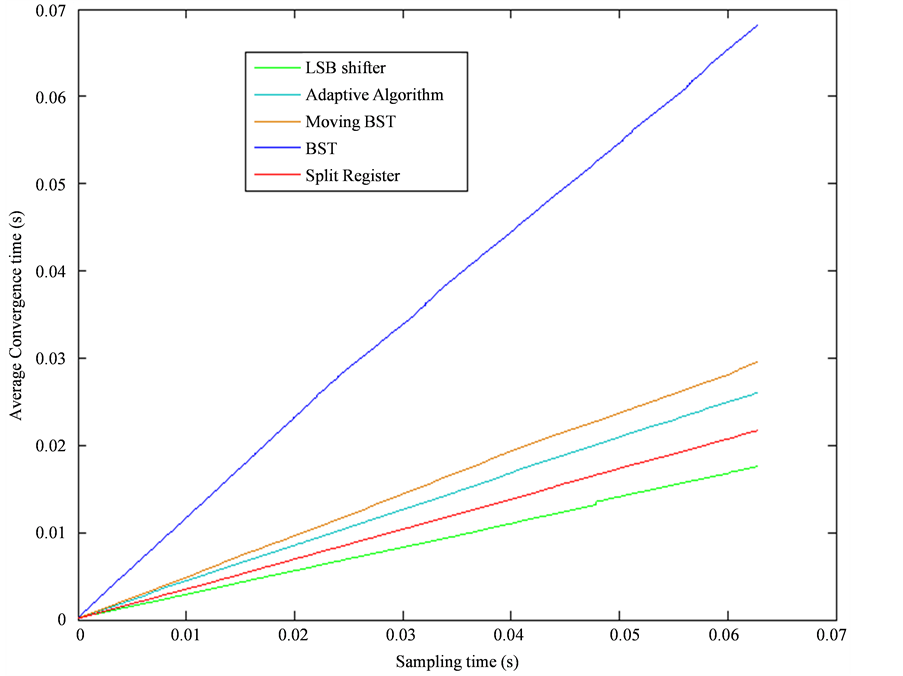
The number of conversions has reduced from 9 to 7 which reduce the power consumption. Using MATLAB it is shown that the number of iterations Moving binary search tree takes to converge to the current value from previous value is on an average 44.12% of that taken by Binary search tree algorithm (as shown in Figure 14).
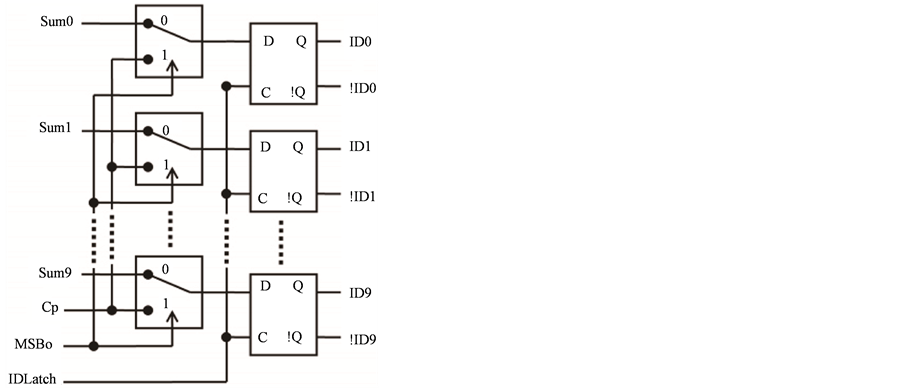
Intermediate latch (Figure 4) drives the DAC during the conversion. In addition, it retains its result after each conversion for range calculator and provides this result as the starting point of moving binary search tree in subsequent conversion. The multiplexers serve to limit the range of moving binary search tree to avoid the search tree from going beyond upper or below lower limits of the ADC full scale range. During each conversion process, the output latch (Figure 5) first provides the preceding result for range calculator and then latches the current result from intermediate latch.
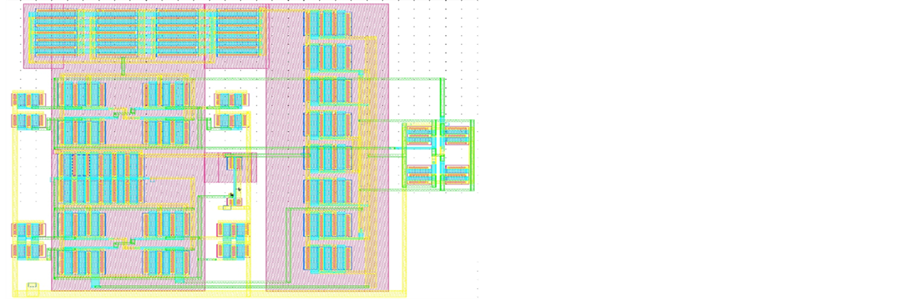
Range calculator consists of a difference-calculating circuit (Figure 6) and a decision-making circuit. The difference-calculating circuit, implemented by full adders, finds the absolute difference between two consecutive signal levels using the complement notation and then passes the result to decision-making circuit. The decision-making circuit decides the size of binary search tree required to cover the changes in signal level for the following conversion. But the moving BST has its own limitations because if the current value is very close to the previous value, then the number of comparisons done to reach the actual target is higher than the difference between the two numbers.
Figure 3. SAR-ADC with moving BST algorithm.
Figure 4. Intermediate latch.
Figure 5. Output latch.
Figure 6. Layout of difference calculating unit and DAC module.
4. Adaptive Algorithm
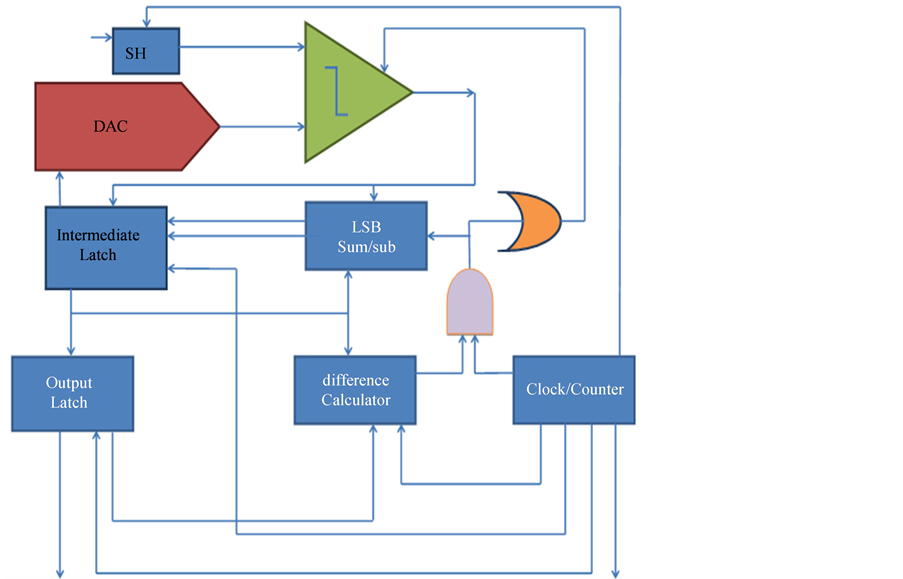
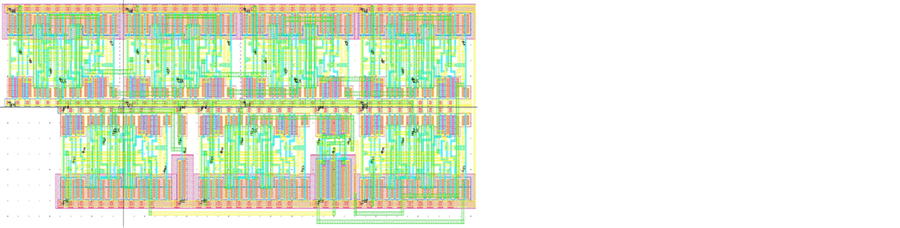
A general linear search method takes a longer time to converge than a BST because the big O notation is of the order of n, which is the worst of all the search algorithms. But why don’t we use the advantage of linear search? When the difference between two consecutive signals is very close, then linear search seems to be a good method to resort to. To implement the moving binary search tree which uses previous result as starting point for conversion, the proposed search tree requires to move “up or down” at any level of the tree. Therefore, a summer (block diagram in Figure 7 and layout in Figure 8) which performs both addition and subtraction is needed. During the successive approximation process, the summer performs addition at the selected bit if the comparator result is logical “1” (i.e. sampled analog input > DAC input) or subtraction at the selected bit if the comparator result is logical “0” (i.e. sampled analog input < DAC input). So now why don’t we combine both, i.e. the advantages of binary and linear search methods? The following example illustrates the mechanism of the circuits. For instance, the two consecutive signals are:
Figure 7. SAR-ADC with adaptive algorithm.
Figure 8. Layout of summer/subtractor unit.
D [10] = 1001100001 (current signal―609).
D [10] = 1001100010 (previous signal―607).
The number of conversions for the adaptive algorithm (Figure 7) to reach to the value of 609 is 2.
1001011111 -> 1001100000 -> 1001100001
This happens because the consecutive signals are so close to each other that the difference between them is less than the number of bits. Hence the linear search is chosen and the value converges in 2 iterations. Figure 2 depicts clearly that for the value to move from m -> q, BST takes 6 iterations i.e. m -> k -> g -> p -> w -> s -> q. But linear search can finish it in 2 iterations, i.e. m -> p -> q. Hence we use a range calculating circuit that finds the difference between current and previous signal, if the difference is less than n-1 [n-number of bits] then linear search will be used, otherwise binary search is used. Since this algorithm has two search algorithms that are used based on the speed at which the input signal changes, it is called as adaptive algorithm.
5. LSB Shifter Algorithm
This is another interesting algorithm we have proposed (Figure 9) which predicts the value based on changing lease significant 0 (Figure 10) or least significant 1 (Figure 11). Just like a moving BST, this algorithm also stores the previous value but instead of doing a regular binary search with the previous value, this algorithm alters individual bits until the required value is reached. When Cp (comparator value) is 1, the least significant 0 is changed to 1 and if the Cp is 0, the least significant 1 is changed to 0. The following example illustrates the mechanism of the circuits. For instance, the two consecutive signals are:
D [10] = 1000011111 (current signal―767).
D [10] = 1000001100 (previous signal―524).
The number of conversions for the LSB shifter to reach to the value of 767 is 3.
(1000001100 -> 1000001101 -> 1000001111 -> 1000011111)
The Moving BST takes 6 conversions to do the same.
(1000001100 -> 1100001100 -> 1010001100 -> 1001001100 -> 1000101100 -> 1000011110 -> 1000011111). While the regular BST takes 9 conversions to do the same (1000000000 -> 1100000000 -> 1010000000 -> 1001000000 -> 1000100000 -> 1000010000 -> 1000011000 -> 1000011100 -> 1000011110 -> 1000011111)
Figure 9. SAR-ADC with LSB shifter algorithm.
Figure 10. Layout of least significant zero modifier.
Figure 11. Layout of least significant one modifier.
But this is not true for all cases. There is a big limitation: Moving BST and BST will be faster if the current signal cannot be reached with “all bit flip 1” or “all bit flip 0” modifications to the previous signal or if the current signal has a difference in two consecutive bits of altering values (e.g. previous signal―0000001100 and current signal―0000010110).
The input from comparator acts as the select signal to the multiplexer shown in the circuits which changes either least significant zero/one based on the analog input to the comparator. This circuit when implemented gave a better FOM than a BST algorithm with a limitation that it gave better performance only for above mentioned input condition and it increased the area.
6. Split Register Algorithm
When the input signal is slowly varying or if the sampling rate is very high, then the current value may be close to the previous value, then why do we need to do the regular BST or moving BST for the entire range of 0 to 1023? Instead, we can do the same moving BST for a smaller range which could eventually reduce the iterations and hence power consumption. So, in this method we are planning to use 8 registers of size 128 each which give 8 boundary values (0, 128, 256... 896). For example, if the current value is 169 then moving BST is done between 128 and 255. Since the signal is slowly varying, the next value will either be in the same register or in the adjacent registers (i.e. first register (0 - 127) or second register (128 - 255) or third register (256 - 383)). Now, how does the algorithm decide which register the value is in? We store the 8 boundary conditions in a memory cell and they are selected using a multiplexer whose control is based on the comparator value. The previous value is in a register and that particular register is known to us. Now three boundary conditions are compared with the analog input, i.e. present, previous and next registers. When the comparator value is 0, it means that the value is in previous register and if it’s one, then it can be in the same or next register.
So based on these comparisons, the register of interest is selected and the moving BST is performed. Will these 8 registers increase the area to a large extent? So these 8 registers are not physical registers, they are just an imaginary assumption hence the initial thought that blocks our mind regarding increase in area is negated. Only the memory cell which stores those 8 boundary conditions is an additional component but the advantage is that, it reduces the number of iterations by 8. Now, why is that we choose 8 imaginary registers and not any other number? Again that depends on how slow the input signal is changing or how fast the sampling rate is. This algorithm is comparable to another similar approach which assumes a short span around the previous value in which it searches and expands its search area if the value is not within that span. But the only difference in this split-register algorithm is that, it finds the search area and then searches thereby saving a lot of iterations (i.e. if the current value is not very close to the previous value then there can be unwanted search iterations used). The layout of the split register module and the block diagram are shown in Figure 12 and Figure 13 respectively.
7. Results
The proposed algorithms are better in terms of power consumption but they would increase the area because of the complex logic structures used and the overall speed is a question which could limit the sampling rate. Hence there is a tradeoff between power, sampling rate, area and cost.
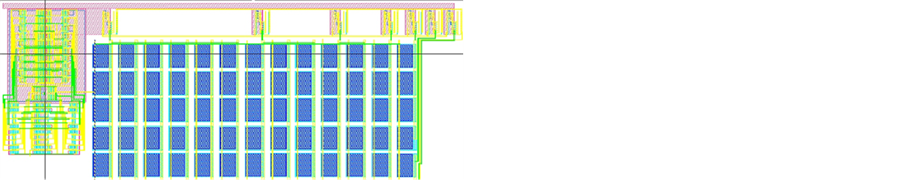
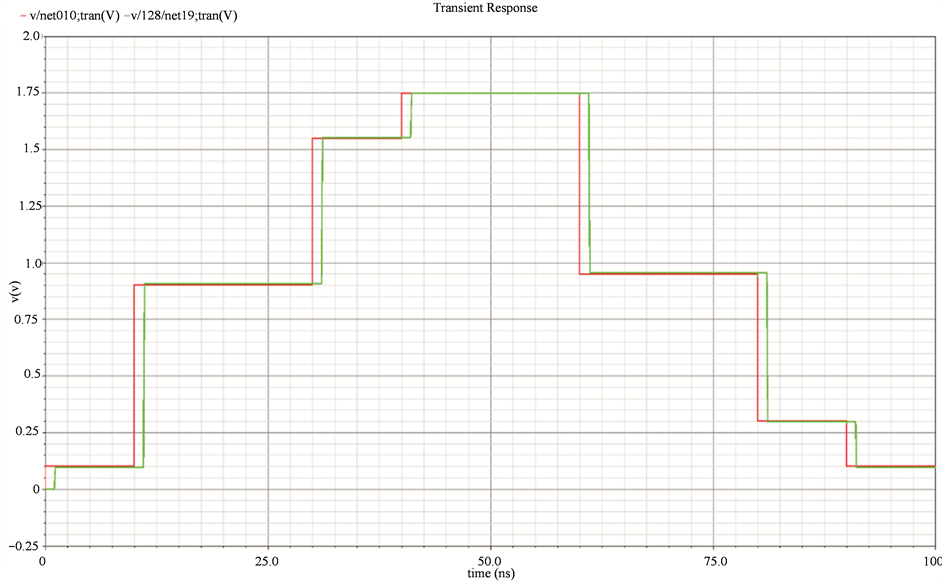
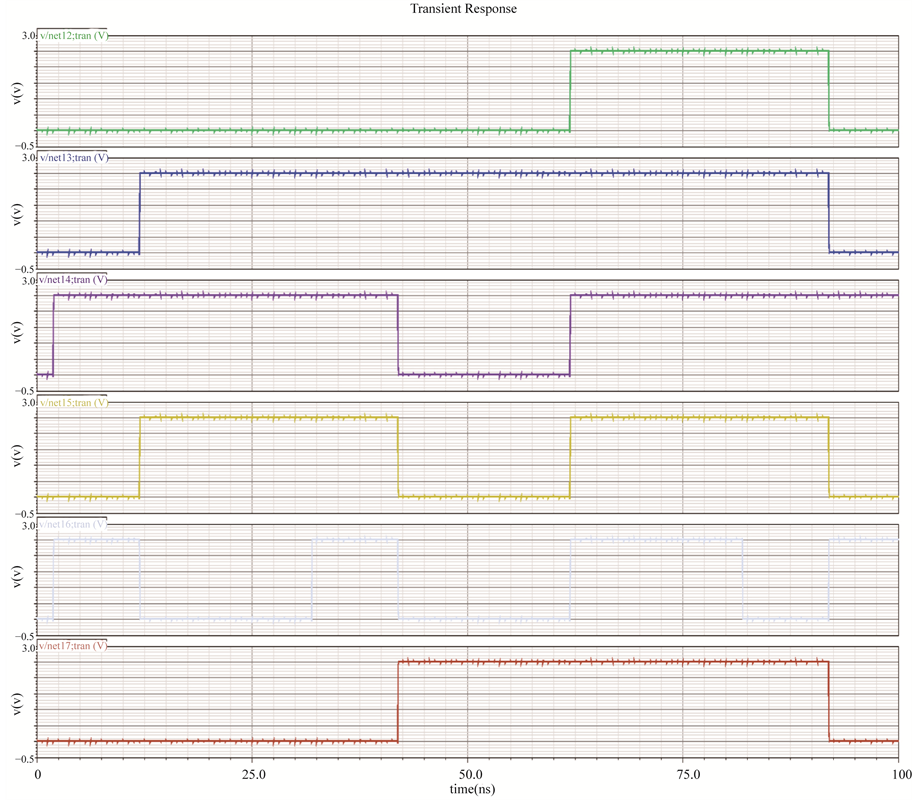
If power consumption was the only concern, then a possible approach of combining all the algorithms would be feasible. Using a range calculator and a difference calculator unit in identifying the type of input signals and the difference in consecutive signals could help in choosing which algorithm to be used. Hence a select signal can be extracted which chooses which algorithm to use for which input signal. The improvement in convergence time is shown in Figure 14. A sample input and its corresponding output for the designed ADC is shown in Figure 15. Figure 16 shows the layout of the proposed ADC. Table 1 shows the comparison of the ADC performance with other state of the art ADCs currently existing. Figure 17 shows the measured output of the ADC chip.
Figure 12. Layout of split register logic module.
Figure 13. SAR-ADC with split register algorithm.
Figure 14. Convergence time of proposed algorithms.
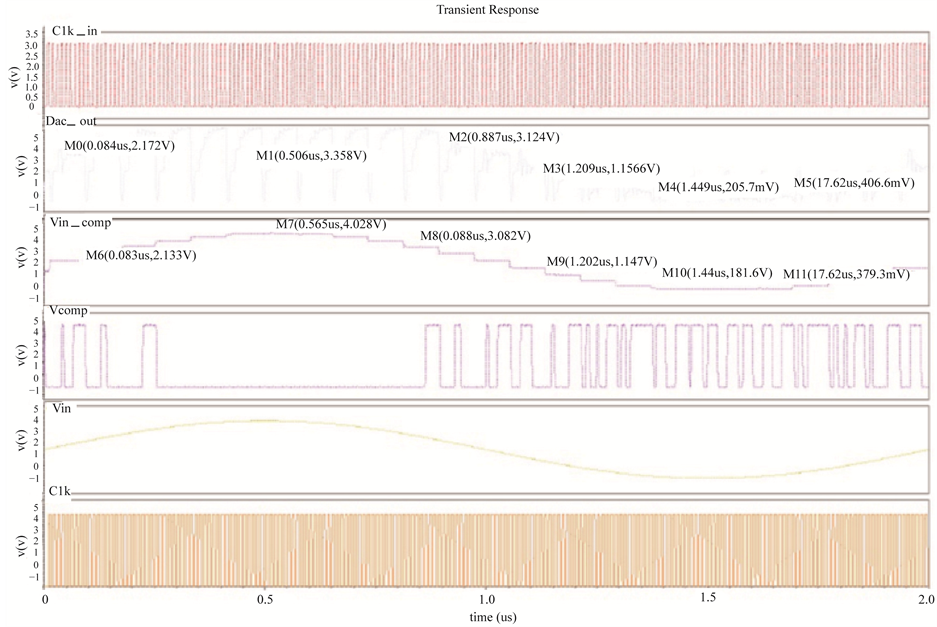
Figure 15. Post layout input/output results at 0.5 GS/s.
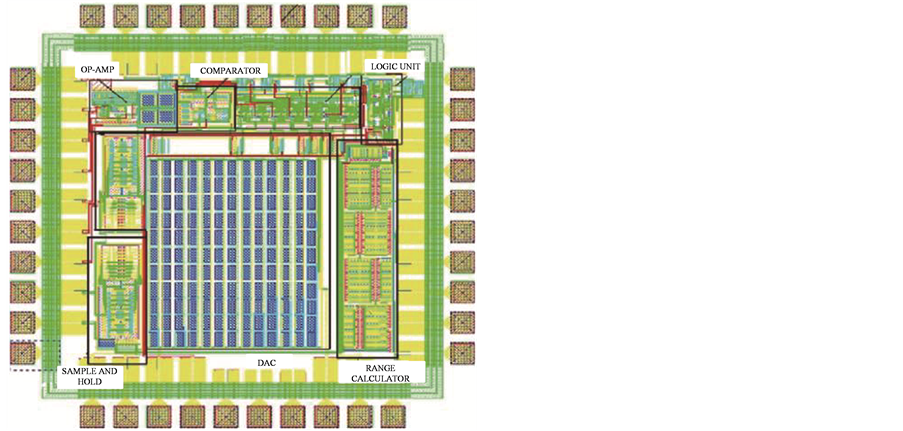
Figure 16. SAR-ADC chip with MBST algorithm logic unit in 65 nm CMOS.
Table 1. Performance comparison with other state of the art ADCs.
Figure 17. Measurement results of the ADC chip.
8. Conclusion
A new approach to low power consumption with different search algorithms and associated control logic has been proposed for the SAR ADC. The proposed modified BST SAR-ADC design chip with 8 bit at 0.8 GS/s consumes 8.532 mW of power in 65 nm CMOS which achieves a power saving of about 56% compared to that of a regular binary search tree SAR-ADC.
Cite this paper
AnanthanarayananParthasarathy, (2015) An 8 Bit 0.8 GS/s 8.352 mW Modified Successive Approximation Register Based Analog to Digital Converter in 65 nm CMOS. Circuits and Systems,06,280-291. doi: 10.4236/cs.2015.612028
References
- 1. Li, P.W., Chin, M.J., Gray, P.R. and Castello, R. (1984) A Ratio Independent Algorithmic Analog-to-Digital Conversion Technique. IEEE Journal of Solid-State Circuits, SC-19, 1138-1143.
http://dx.doi.org/10.1109/jssc.1984.1052233 - 2. Ohara, H., et al. (1987) A CMOS Programmable Self-Calibrating 13-b Eight Channel Data Acquisition Peripheral. IEEE Journal of Solid-State Circuits, SC-22, 930-938.
http://dx.doi.org/10.1109/JSSC.1987.1052840 - 3. Shih, C.C., et al. (1986) Reference Refreshing Cyclic Analog-to-Digital and Digital-to-Analog Converters. IEEE Journal of Solid-State Circuits, SC-21, 544-554.
http://dx.doi.org/10.1109/JSSC.1986.1052570 - 4. Liew, W.-S., Yao, L.B. and Lian, Y. (2008) A Moving Binary Search SAR-ADC for Low Power Biomedical Data Acquisition System.
- 5. Tousi, Y.M., Li, G., Hassibi, A. and Afshari, E. (2009) A 1 mW 4 Bit 1 Gs/s Delay-Line Based Analog to Digital Converter. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS), 24-27 May 2009, 1121-1124.
- 6. Yang, J., Niang, T.L. and Broderson, R.W. (2010) A 1 GS/s 6 bit 6.7 mW Successive Approximation ADC Using Asynchronous Processing. IEEE Journal of Solid-State Circuits, 45, 1469-1478.
http://dx.doi.org/10.1109/JSSC.2010.2048139 - 7. Ginsburg, B.P. and Chandrakasan, A.P. (2008) Highly Interleaved 5-Bit, 250-M Sample/s, 1.2-mW ADC with Redundant Channels in 65-nm CMOS. IEEE Journal of Solid-State Circuits, 43, 2641-2650.
http://dx.doi.org/10.1109/JSSC.2008.2006334 - 8. Park, S., Palaskas, Y. and Flynn, M.P. (2007) A 4-GS/s 4-Bit Flash ADC in 0.18 um CMOS. IEEE Journal of Solid-State Circuits, 42, 1865-1872.
http://dx.doi.org/10.1109/JSSC.2007.903053 - 9. Shan, J., Do, M.A., Yeo, K.S. and Lim, W.M. (2008) An 8-Bit 200-M Sample/s Pipelined ADC with Mixed-Mode Front-End S/H Circuit. IEEE Transactions on Circuits and Systems—I: Regular Papers, 55.
- 10. Liu, C.-C., Chang, S.-J. and Huang, G.-Y. (2010) A 10-Bit 50 MS/s SAR ADC with a Monotonic Capacitor Switching Procedure. IEEE Journal of Solid-State Circuits, 45, 731.
http://dx.doi.org/10.1109/JSSC.2010.2042254