Received 4 March 2015; accepted 19 May 2015; published 22 May 2015

ABSTRACT

This paper presents a low-phase-noise LC voltage-controlled oscillator (LC-VCO) with top resistive biasing in subthreshold region. The subthreshold LC-VCO has low-power and low-phase-noise due to its high transconductance efficiency and low gate bias condition. The top resistive biasing has more benefit with the feature of phase noise than MOS current source since it can support the low-noise characteristics and large output swing. The LC-VCO designed in 130-nm CMOS process with 0.7-V supply voltage achieves phase noise of −116 dBc/Hz at 200 kHz offset with tuning range of 398 MHz to 408 MHz covering medical implant communication service (MICS) band.

Keywords:

VCO, Resistive Biasing, Current Source, CMOS Integrated Circuit, Phase Noise, MICS Band

1. Introduction

Integrated LC oscillators are important building blocks in the implementation of radio frequency (RF) front-end modules to provide a stable local oscillator (LO) signal for modulation/demodulation or up/down frequency conversion. RF transceivers for implanted medical device require miniaturized forms with low-power consumption and fully integration. The medical implant communication service (MICS) band in the frequency range of 402 MHz to 405 MHz is widely used for medical RF transceivers because the MICS band signals have reasonable propagation characteristics in human body and are well suited for achieving a good trade-off between size and power. Furthermore, the use of MICS band does not pose a significant risk of interference to other frequencies within or close to this band. The phase noise requirement for an oscillator operating in MICS band is less than −100 dBc/Hz at 200 kHz offset frequency [1] .

One of the major challenges in the design of RF front-end modules is implementation of fully integrated low- power, low-phase-noise voltage-controlled oscillators (VCOs). The CMOS devices operating in subthreshold region have an advantage of higher transconductance to power dissipation ratio with decent noise performance in comparison with the strong inversion region. Therefore, the subthreshold VCO achieves low-power and low-phase-noise characteristics. The circuits designed with MOS transistors biased in the subthreshold region operate with lowered voltage headroom, resulting in lower supply voltage. However, the phase noise performance is degraded due to the small amplitude at low supply voltages and it is recognized that the active current source for biasing purpose introduces noise performance degradation [2] [3] . There have been many efforts to improve the phase noise performance by improving the quality (Q) factor of the resonator or reducing the noise power [4] [5] . In this work, we focus on the current biasing technique in subthreshold region for better performance. The subthreshold-biased LC-VCO and resistive biasing technique are employed to achieve low-voltage operation and low phase noise.

This paper presents the analysis of phase noise performance through various biasing techniques, and a low- phase-noise LC-VCO is designed using resistive biasing instead of active current source scheme. The top resistive biasing is employed for low-phase-noise and low-voltage operation because of its inherent advantage of low effective noise and large voltage swing. This circuit has been designed in 130-nm CMOS technology with 0.7-V supply voltage. This paper is organized as follows. Section 2 presents the phase noise analysis in accordance with various biasing techniques. Section 3 describes the circuit design, and presents the simulation results. Finally, conclusions are drawn in Section 4.

2. Phase Noise Analysis of Biasing Techniques

There are many ways to realize the integrated LC-VCOs. For the analysis of the current biasing techniques, an NMOS cross-coupled differential pair is used for the core oscillator design, which has an advantage of common-mode noise suppression and low-voltage operation. The different cases of current biasing techniques in differential LC-VCO are shown in Figure 1. 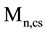In general, the active biasing with MOS current sources, and, (Figure 1(a) and Figure 1(b)) and passive biasing with resistors, and, (Figure 1(c) and Figure 1(d)) are used to supply the bias current.

The phase noise in harmonic oscillators based on the linear time-variant (LTV) analysis approach is expressed as [6] [7]

(1)

where is the offset angular frequency, is the total capacitance of LC resonator, A_T is the oscillation amplitude across the LC resonator, and the effective noise power 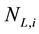is given by [7]

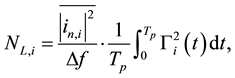(2)

where T_p is the oscillation time period, is the noise current power spectral density per unit frequency

generated by the i-th device, and 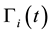is the impulse sensitivity function (ISF) representing the time-varying sensitivity of the oscillator phase to perturbations. ISF is a dimensionless, amplitude-independent periodic function which describes how much phase shift occurs from applying a unit impulse at any point of time. The phase noise depends on the reciprocal of the oscillation amplitude. Based on the simple analytical model similar to [8] , the oscillation amplitude A_T is given by

(3)

where 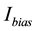is the bias current and R_T is the equivalent parallel resistance of the LC resonator. Among the components of LC resonator, Q factor of inductor is more dominant than of capacitor because inductor has lower Q factor than that of capacitor. So, R_T can be calculated as

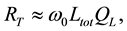(4)

where 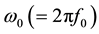is the oscillation angular frequency, is the total inductance, and Q_L is the Q factor of inductor. This is the reason that the usual design practices try to maximize both the available oscillation amplitude and the Q factor in order to reduce the phase noise. Also, the effective noise power proportionally links the phase noise performance and has relevance to the noise source which depends on the biasing techniques.

2.1. Effective Noise

Lower effective noise improves phase noise performance, and it depends on the noise source. The total effective noise of LC-VCO using MOS current source (Figure 1(a) and Figure 1(b)), , is expressed as [9]

(5)

where, , and are the effective noise of LC resonator, differential-pair MOS devices, and MOS current source, respectively. is the Boltzmann’s constant, T is the absolute temperature, is the transconductance of MOS current source, is the channel noise coefficient of MOS device, and is a parameter related to the transition time interval between the switching action of differential-pair devices M₁ and M₂ in the case of MOS current source. In this work, is different from 4/9 in the literature [10] because of the subthreshold operation. The value of is determined from simulation results of phase noise. From the simulation results, and are obtained as 0.5 and 0.2, respectively. This equation describes three noise contributions. The first and second terms describe the noise contribution from the LC resonator loss and the differential-pair MOS devices, respectively. The third term describes the noise from the MOS current source. In typical LC-VCOs operating at high current levels with moderate-to-high Q factor, the MOS current source noise dominates phase noise over other noise sources [2] . There have been many efforts to reduce the phase noise by using a high value inductor in series with the current source in order to isolate the source node of differential-pair devices and current source, thus obtaining a composite current generator [10] [11] . In such an approach, however, the noise of the tail transistor still affects at the source node of differential-pair MOS devices in spite of wasting area for the added inductor.

To reduce the noise from the MOS current source, a low-value resistor is employed as a practical biasing technique for LC-VCOs. In the case of using a resistor as current source, the thermal noise caused by MOS current source can be replaced by the thermal noise of the bias feeding resistor. Here, considering the differential- pair MOS switching action in resistive biasing case, the total effective noise for LC-VCO using resistive biasing (Figure 1(c) and Figure 1(d)), , can be expressed as

(6)

where is the effective noise of bias feeding resistor, is the bias feeding resistance for each bi-

asing position (top and bottom), and is a parameter related to the transition time interval between the switching action of differential-pair devices M₁ and M₂ in the case of resistive biasing. The value of is determined from simulation results of phase noise. From the simulation results, and are obtained as 0.65 and 0.8, respectively. Similar to the MOS current source case, in the above equation the first and second terms of noise contribution are from the LC resonator loss and the differential-pair MOS devices, respectively. The third term indicates the contribution from the thermal noise of bias feeding resistor.

Figure 2(a) represents the effective noise contribution for different biasing techniques. Typically, an NMOS transistor has a larger drain noise current than a PMOS transistor under the same drain current. So, the choice of using PMOS transistors as current source reduces the effective noise. However, PMOS current source case still has a large effective noise. Contrarily, resistive biasing techniques show low effective noise as they avoid the use of noisy MOS current source. Thermal noise from the bias feeding resistor as current source is low, and thereby it has small influence on phase noise.

2.2. Oscillation Amplitude

From the discussion in the above section, increasing oscillation amplitude reduces the phase noise. In Equation (3), the oscillation amplitude in LC-VCO is proportional to the equivalent parallel resistance of the LC resonator R_T and bias current. As the LC-VCOs shown in Figure 1 have the same LC resonator, the current in each VCO dominates the improvement of oscillation amplitude.

Figure 2(b) shows I-V characteristic of the differential-pair part of the LC-VCO, which realizes small-signal negative resistance. In the bottom resistive biasing, this part is equivalent to a couple of common-source MOS devices with source degeneration resistor. The instantaneous gate-source voltage of the common-source MOS devices for bottom and top resistive biasing techniques (and) have a relationship as follows:

(7)

where is the voltage change of bottom resistor from biasing point. MOS drain current in subthreshold re-

gion is proportional to the exponential of the gate-source voltage. The gate-source voltage in bottom biasing is attenuated by the voltage drop across the bottom resistor. The subthreshold drain currents for two resistive biasing have the following relationship

(8)

where and are the drain current of top biasing and bottom biasing, respectively. I₀ is the technology current factor, L and W are the effective channel length and width, V_TH is the threshold voltage, n is the subthreshold slope factor, is the thermal voltage, and q is the electronic charge (U_T = 25.9 mV at room temperature). The above equation can explain that the top biasing has more current than bottom biasing as shown in Figure 2(b). The oscillation amplitude by biasing techniques is shown in Figure 2(c). The top biasing has larger oscillation amplitude than bottom biasing according to the current characteristics of the differential- pair, and thereby improves the phase noise performance.

2.3. Comparison

Figure 2(d) shows the phase noise comparison for different biasing techniques. The phase noise results are obtained from the periodic steady-state circuit simulation with various current conditions. The resistive biasing techniques, which do not use noisy MOS current source, have 60% less effective noise than NMOS current source case. The low thermal noise introduced by a biasing resistance lower than nearly 1 kW does not influence the oscillator spectral purity. In aspect of biasing position, the bottom biasing technique degrades the oscillation amplitude due to the degradation of drain current. As a result, top resistive biasing technique has higher oscillation amplitude of 1.15 to 1.35 times than other biasing techniques. Taken together, the top resistive biasing technique has better phase noise performance because of smaller effective noise and large output swing.

3. Circuit Design and Simulation Results

In this study, the top resistive biasing is applied to design the LC-VCO operating at a 0.7-V supply for the MICS band. The structure of NMOS cross-coupled differential LC-VCO with top resistive biasing is shown in Figure 3(a). The MOS transistors optimally biased in subthreshold region are utilized to provide enough transconductance for a given bias condition, resulting in reduction of the power dissipation of the LC-VCO. Additionally, a lower gate bias voltage would increase the maximum achievable oscillation amplitude [7] and thereby improves the phase noise performance. The dual-layer spiral inductor and varactor are used for the LC resonator. The dual-layer spiral inductor has high Q factor value because of its lower series resistance [12] . The inductance of spiral inductor is 8.18 nH. The capacitance corresponding to inductance is 15.4 pF, and the varactors have a capacitance range of 0.1 pF to 0.6 pF. The Q factor value of LC resonator is approximately 8 at 400 MHz. Figure 3(b) shows the phase noise and current consumption in accordance with top biasing resistance. With the increase in current consumption, the phase noise performance is improved. For low power consumption, the target of current consumption is set under 1 mA and the top bias feeding resistance is approximately 400 W which has small influence on the phase noise. The power consumption of the designed LC-VCO is 700 μW with 0.7-V supply voltage. Figure 3(c) shows the phase noise performance. The designed LC-VCO using top resistive biasing oscillating around 400 MHz has a phase noise of −116 dBc/Hz at 200 kHz offset frequency meeting the MICS band phase noise requirement which is less than −100 dBc/Hz at 200 kHz offset frequency. The tuning range of designed LC-VCO is 398 MHz to 408 MHz covering the MICS band (402 MHz ~ 405 MHz), as shown in Figure 3(d).

4. Conclusion

A low-voltage low-phase-noise LC-VCO operating in subthreshold region using top resistive biasing is presented. The subthreshold-biased LC-VCO achieves low-power consumption, and the lower gate bias provides the phase noise improvement. The LC-VCO using top resistive biasing operates from 398 MHz to 408 MHz and exhibits a phase noise of −116 dBc/Hz at 200 kHz offset frequency with an improvement of 1 dB to 6 dB compared with other biasing techniques in similar conditions. Designed LC-VCO consumes 700 μW from a 0.7-V

supply. In comparison of the biasing techniques, the top resistive biasing has least effective noise power because of the elimination of noisy MOS current source, and has a large output swing because of no current degradation. Therefore, the top resistive biased LC-VCO realizes the low-voltage operation with better phase noise performance.

Acknowledgements

The IC in this study is designed as part of the chip fabrication program of the VDEC at the University of Tokyo in collaboration with Cadence Design Systems.

References