Circuits and Systems
Vol. 3 No. 1 (2012) , Article ID: 16643 , 6 pages DOI:10.4236/cs.2012.31003
A Survey on the Stability of 2-D Discrete Systems Described by Fornasini-Marchesini Second Model
Electronics and Communication Engineering Department, Motilal Nehru National Institute of Technology, Allahabad, India
Email: manishtiwari_me@yahoo.com, amit_dhawan2@rediffmail.com
Received November 1, 2011; revised December 1, 2011; accepted December 11, 2011
Keywords: 2-D Discrete Systems; FM Second Model; Asymptotic Stability; Lyapunov Methods
ABSTRACT
A key issue of practical importance in the two-dimensional (2-D) discrete system is stability analysis. Linear state-space models describing 2-D discrete systems have been proposed by several researchers. A popular model, called Fornasini-Marchesini (FM) second model was proposed by Fornasini and Marchesini in 1978. The aim of this paper is to present a survey of the existing literature on the stability of FM second model.
1. Introduction
There have been a continuously growing research interests in two-dimensional (2-D) systems due to their applications in various important areas such as multi-dimensional digital filtering, signal processing, seismographic data processing, thermal processes, gas absorption, water stream heating etc. [1-4]. In a 2-D discrete system, information propagates in two independent directions as a result of which the system dynamics may be represented as a function of two independent integer variables. Many researchers have made an attempt to describe the 2-D system dynamics in terms of linear state-space models for 2-D discrete systems [5-7]. The 2-D models that have received considerable attention are Roesser model [5], Fornasini-Marchesini (FM) first model [6] and FM second model [7].
Stability analysis and stabilization are the main issues in the design of any control system. Stability issues of 2-D systems have been considered by many researchers [8-18]. With the introduction of state-space models of 2-D discrete systems, various Lyapunov equations have emerged as powerful tools for the stability analysis and stabilization of 2-D discrete systems. Lyapunov based sufficient conditions for the stability of 2-D discrete systems have been studied in [19-26]. When the dynamics of practical systems are represented using state-space models, errors are inevitable as the actual system parameters would be different than the estimated system parameters, i.e., the model parameters. These errors arise due to the approximations made during the process modeling, differences in presumed and actual process operating points, change in operating conditions, system aging etc. Control designs based on these models, therefore, may not perform adequately when applied to the actual industrial process and may lead to instability and poor performances. This has motivated the study of robust control for the uncertain 2-D discrete systems. The aim of robust control is to stabilize the system under all admissible parameter uncertainties arising due to the errors around the nominal system. Many significant results on the solvability of robust control problem for the uncertain 2-D discrete systems have been proposed in [27-33].
The issue in robust control design is twofold: first is to design a robust controller to ensure the stability of uncertain systems and the other is to guarantee a certain performance level under the presence of uncertainties. The latter is called as guaranteed cost control problem which has the advantage of providing an upper bound on the closed-loop cost function (performance index). Consequently, a guaranteed cost controller not only stabilizes the uncertain system but also guarantees that the value of closed-loop cost function is not more than the specified upper bound for all admissible parameter uncertainties. Based on this idea, many significant results have been obtained for the uncertain 2-D discrete systems [34-39].
Study and analysis of 2-D discrete systems under the presence of noise is another research area of great interest where it is usually necessary to estimate the state variables from the system measurement data. One of the celebrated approaches is Kalman filtering [40] which is based on two fundamental assumptions that the system under consideration is exactly known and a priori information on the external noises (like white noise, etc.). However, in many practical situations, these assumptions may be invalid. This has motivated the 2-D signal estimation using 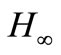 filtering technique. The advantage of
filtering technique. The advantage of 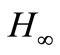 filtering is that the noise sources can be arbitrary signals with bounded energy, or bounded average power instead of being Gaussian. Hence,
filtering is that the noise sources can be arbitrary signals with bounded energy, or bounded average power instead of being Gaussian. Hence,  filtering tends to be more robust when there exist additional parameter disturbances in models and it is very appropriate in a number of practical situations [41]. The 2-D filtering approach with
filtering tends to be more robust when there exist additional parameter disturbances in models and it is very appropriate in a number of practical situations [41]. The 2-D filtering approach with  performance measure has been developed in [41-47].
performance measure has been developed in [41-47].
The linear matrix inequalities (LMIs) have been evolved as a powerful technique to formulate various control designs [48]. The advantage of LMI technique is that the problem of testing the stability of a system can be formulated in terms of existence of a certain LMI (e.g., see [49]). Since solving LMIs is a convex optimization problem, such formulations offer an efficient numerical method to deal with the problems that lack an analytical solution. These LMIs can be solved efficiently by Matlab LMI tool box [50].
In this paper, our main focus is on the FM second model which is one of the most investigated models for the study and analysis of 2-D discrete systems. A brief survey of the existing literature on the stability of the 2-D discrete systems described by FM second model has been presented in this paper. The paper is organized as follows: Section 2 presents the description of 2-D system described by FM second model. A brief survey and main results on the stability of FM second model has been discussed in Section 3. Finally, some concluding remarks are given in Section 4.
Throughout the paper the following notations are used: The Closed unit disc is represented by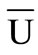 ,
,  represents the unit circle,
represents the unit circle, 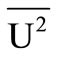 denotes the closed unit bidisc. The superscript T stands for matrix transposition,
denotes the closed unit bidisc. The superscript T stands for matrix transposition, 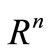 denotes real vector space of dimension n,
denotes real vector space of dimension n, 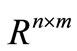 is the set of n ´ m real matrices, 0 denotes null matrix or null vector of appropriate dimension,
is the set of n ´ m real matrices, 0 denotes null matrix or null vector of appropriate dimension, 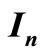 is the
is the 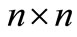 identity matrix, diag (…) stands for a block diagonal matrix, G > 0 stands for the matrix G is positive definite,
identity matrix, diag (…) stands for a block diagonal matrix, G > 0 stands for the matrix G is positive definite, 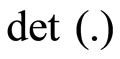 denotes determinant of a matrix,
denotes determinant of a matrix, 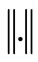 denotes induced matrix norm,
denotes induced matrix norm, 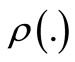 stands for spectral radius of a matrix,
stands for spectral radius of a matrix, 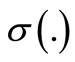 stands for spectrum of a matrix, for a matrix pair
stands for spectrum of a matrix, for a matrix pair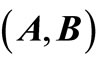 ,
, 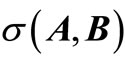 denote the set of all its generalized eigenvalues i.e.
denote the set of all its generalized eigenvalues i.e.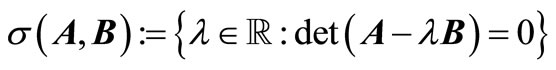 , where
, where 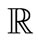 is the set of complex numbers. Further,
is the set of complex numbers. Further, 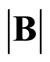 stands for the matrix
stands for the matrix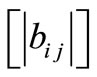 , and
, and 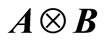 represents Kronecker product of the matrices
represents Kronecker product of the matrices  and
and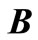 .
.
2. Description of FM Second Model
Consider the following 2-D discrete system represented by FM second model [7]:
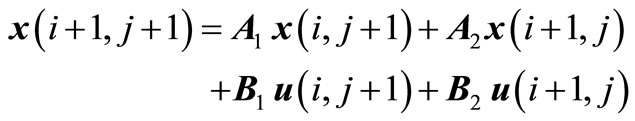 , (1a)
, (1a)
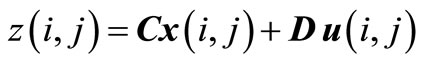 , (1b)
, (1b)
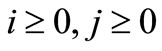 (1c)
(1c)
where 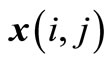 is an
is an 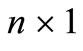 state vector,
state vector, 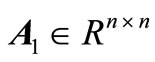 ,
, 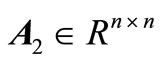 ,
, 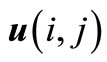 is
is  input vector,
input vector, 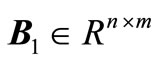 ,
, 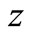
 is a scalar output,
is a scalar output, 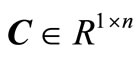 and
and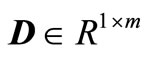 . It is understood that the above system has a finite set of initial conditions [2] i.e., there exist two positive integers
. It is understood that the above system has a finite set of initial conditions [2] i.e., there exist two positive integers 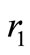 and
and 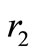 such that
such that
 (1d)
(1d)
The equilibrium  of system (1) is said to be globally asymptotically stable [2] if
of system (1) is said to be globally asymptotically stable [2] if
 (2)
(2)
The transfer function of system (1) is given as
 (3)
(3)
If we define,
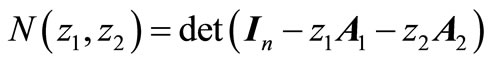 , (4a)
, (4a)
then the state-space model (1) is asymptotically stable [7] if and only if
 (4b)
(4b)
where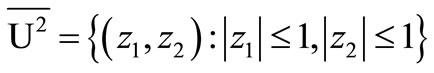 .
.
3. A Brief Survey
The problem of asymptotic stability of system (1) has been studied by many researchers [51-59]. Lyapunov based sufficient condition for the stability of system (1) has been investigated in [51] and it is proposed that the system (1) is asymptotically stable if there exist an 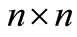 symmetric matrix
symmetric matrix 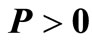 such that
such that
 , (5a)
, (5a)
provided
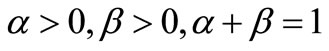 (5b)
(5b)
Reference [52] presents a stability test for system (1) which states that
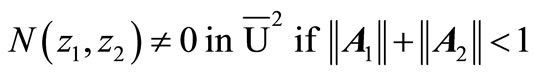 , (6)
, (6)
where 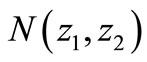 is defined in (4a). Further, based on the 2-D Lyapunov equation approach, the problem of stability margin has also been studied in [52].
is defined in (4a). Further, based on the 2-D Lyapunov equation approach, the problem of stability margin has also been studied in [52].
Studies in [53] has illustrated that there are a large number of systems that are stable but their stability cannot be assured by (5). That is, no values of 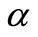 and
and  can be found to satisfy (5) for a large number of systems to confirm their stability. The result proposed in [51] is made into more generalized form in [53] and it has been proposed that the system (1) is asymptotically stable if there exist
can be found to satisfy (5) for a large number of systems to confirm their stability. The result proposed in [51] is made into more generalized form in [53] and it has been proposed that the system (1) is asymptotically stable if there exist  symmetric matrices
symmetric matrices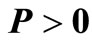 ,
, 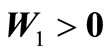 ,
, 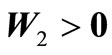 ,
, 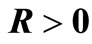 such that
such that
 (7a)
(7a)
and
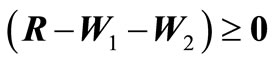 . (7b)
. (7b)
As noted in [53], (5) can be recovered as a special case of (7). It is also mentioned in [53], that without loss of generality 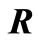 can be assigned to
can be assigned to 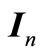 and an equivalent condition of stability can be given as: The system (1) is asymptotically stable if there exist
and an equivalent condition of stability can be given as: The system (1) is asymptotically stable if there exist 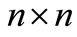 symmetric matrices
symmetric matrices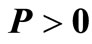 ,
, 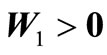 and
and 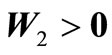 such that
such that
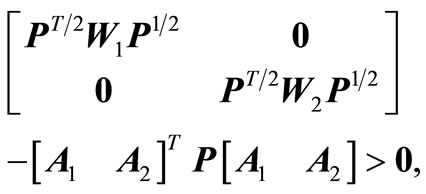 (8a)
(8a)
and
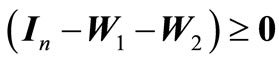 . (8b)
. (8b)
In [54], sufficient conditions to guarantee the asymptotic stability of system (1) are presented. The first criterion states that for system (1) to be asymptotically stable it is sufficient that 1) 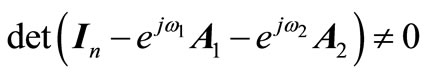 , (9a)
, (9a)
and 2) there exist an 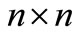 symmetric matrix
symmetric matrix  such that
such that
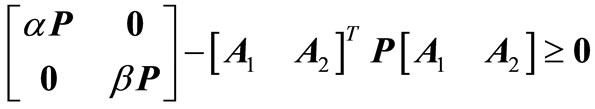 , (9b)
, (9b)
provided
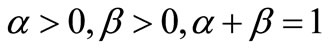 .
.
Here 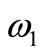 and
and 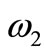 are the horizontal and vertical radian frequencies, respectively.
are the horizontal and vertical radian frequencies, respectively.
The second criterion states that the system (1) is asymptotically stable if there exist 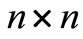 symmetric matrices
symmetric matrices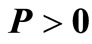 ,
,  and
and 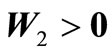 such that
such that
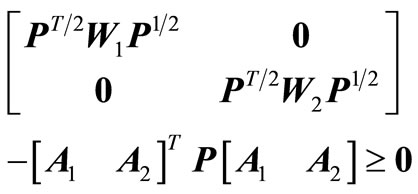 (10a)
(10a)
and
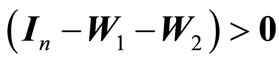 . (10b)
. (10b)
At this point, readers are advice to observe the differences between (8) and (10). Furthermore, the relationship between 2-D Lyapunov approach and stability margin has also been investigated in [54].
Another 2-D Lyapunov equation, which is in a more general form, for asymptotic stability of system (1) has been presented in [55]. According to [55], the system (1) is asymptotically stable provided there exist 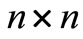 symmetric matrices
symmetric matrices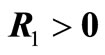 ,
,  such that
such that
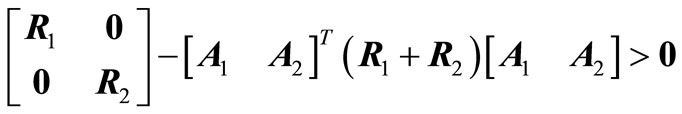 . (11)
. (11)
Further, it has been shown that the Lyapunov matrix Inequality (11) can be expressed in a succinct form using parallel addition of positive definite matrices and an equivalent condition of stability can be given as: The system (1) is asymptotically stable if there exist a pair of  positive definite matrices
positive definite matrices ,
, 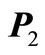 such that
such that
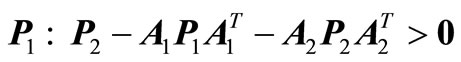 , (12)
, (12)
where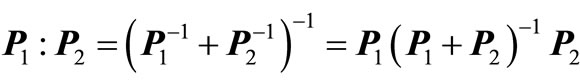 ,
, 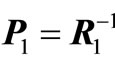 ,
,
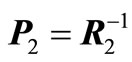 and
and 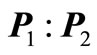 is known as parallel addition of
is known as parallel addition of  and
and . It is interesting to note that as a rough approximation, the terms
. It is interesting to note that as a rough approximation, the terms  and
and 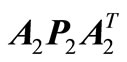 makes out the next time energy along the one-dimensional dynamics; it then follows that the sum of total next time energy should be less than the modified present energy represented by
makes out the next time energy along the one-dimensional dynamics; it then follows that the sum of total next time energy should be less than the modified present energy represented by  for the 2-D system (1) to be asymptotically stable. It has been further illustrated that in spite of its outward beauty, the Inequality (12) is rather complicated even for smaller values of
for the 2-D system (1) to be asymptotically stable. It has been further illustrated that in spite of its outward beauty, the Inequality (12) is rather complicated even for smaller values of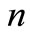 .
.
In [56], the estimation of stability robustness for the FM second model has been studied and it is mentioned that the use of the stability bounds through the 2-D Lyapunov approach is limited in application. Studies in [57] explore numerically efficient stability test methods for 2-D discrete systems based on matrix pencil approach. The necessary and sufficient conditions for the stability 2-D system have been formulated as a problem of solving the generalized eigenvalues of a constant matrix pair. As stated in [57], the system (1) is stable if and only if
 is stable (13a)
is stable (13a)
and
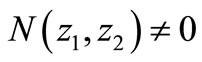 for all
for all 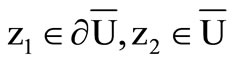 (13b)
(13b)
Here the stability of 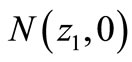 is equivalent to
is equivalent to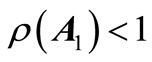 . If we define the matrices
. If we define the matrices
 , (14a)
, (14a)
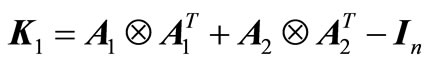 , (14b)
, (14b)
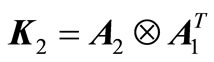 , (14c)
, (14c)
then, the necessary and sufficient condition for the stability is as follows: The 2-D system (1) is stable if and only if 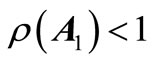 and additionally one of the following conditions holds:
and additionally one of the following conditions holds:
1)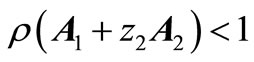 , for all
, for all . (15a)
. (15a)
2)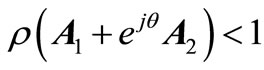 , for all
, for all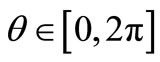 . (15b)
. (15b)
3)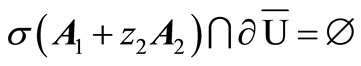 , for all
, for all 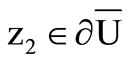
and
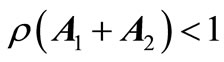 . (15c)
. (15c)
4) 
and
 , (15d)
, (15d)
where
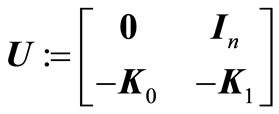 and
and
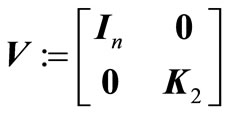 .
.
Further, the authors in [57] have also claimed that the above stability tests tend to provide high computational accuracy.
An LMI based necessary and sufficient condition for the positive FM second model has been presented in [58]. If all the elements of system matrices 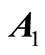 and
and are positive then the system (1) will be asymptotically stable if and only if one of the following equivalent conditions holds:
are positive then the system (1) will be asymptotically stable if and only if one of the following equivalent conditions holds:
1) The LMI
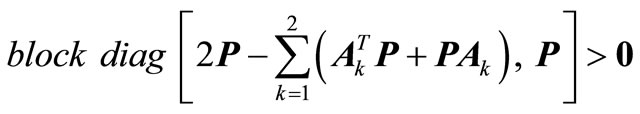 , (16a)
, (16a)
is feasible with respect to the diagonal matrix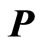 .
.
2) The LMI
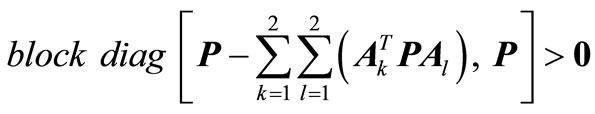 , (16b)
, (16b)
is feasible with respect to the diagonal matrix .
.
The Lyapunov based sufficient condition for the stability of system (1) under shift delays has been discussed in [59]. It has been proposed that system (1) under shift delays is asymptotically stable if there exist 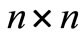 symmetric matrices
symmetric matrices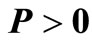 ,
, 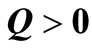 ,
,  ,
,  such that
such that
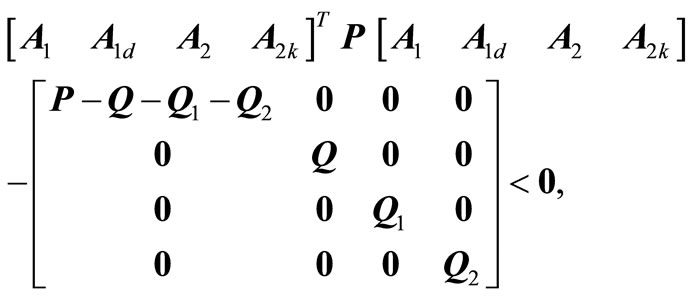 (17)
(17)
where  and
and 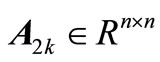 are delay matrices. Based on condition (17), the problem of robust stability and stabilization of 2-D discrete shift-delayed system described by the FM second model has also been addressed.
are delay matrices. Based on condition (17), the problem of robust stability and stabilization of 2-D discrete shift-delayed system described by the FM second model has also been addressed.
In [60], the problem of robust guaranteed cost control for 2-D discrete system under shift delays has been considered and sufficient condition for the existence of robust guaranteed cost controller via static-state feedback has been derived.
In [61], some technical errors that have occurred in the main results of [60] are pointed out and corrected.
4. Concluding Remarks
A review on the stability of 2-D discrete systems described by FM second model has been presented in this paper. The Lyapunov based approach has emerged as a popular approach to study the stability properties of such systems. The 2-D Lyapunov based stability conditions discussed so far in literature are only sufficient conditions. The Lyapunov based necessary and sufficient condition for the stability of 2-D discrete systems remains an open and challenging problem.
5. Acknowledgements
The authors wish to thank the associate editor and the anonymous reviewers for their constructive comments and suggestions.
REFERENCES
- N. K. Bose, “Applied Multidimensional System Theory,” Van Nostrand Reinhold, New York, 1982.
- T. Kaczorek, “Two-Dimensional Linear Systems,” SpringerVerlag, Berlin, 1985.
- W.-S. Lu and A. Antoniou, “Two-Dimensional Digital Filters,” Marcel Dekker, Electrical Engineering and Electronics, Vol. 80, New York, 1992.
- R. N. Bracewell, “Two-Dimensional Imaging,” PrenticeHall Signal Processing Series, Prentice-Hall, Englewood Cliffs, 1995.
- R. P. Roesser, “A Discrete State-Space Model for Linear Image Processing,” IEEE Transactions on Automatic Control, Vol. 20, No. 1, 1975, pp. 1-10. doi:10.1109/TAC.1975.1100844
- E. Fornasini and G. Marchesini, “State-Space Realization Theory of Two Dimensional Filters,” IEEE Transactions on Automatic Control, Vol. 21, No. 4, 1976, pp. 484-492. doi:10.1109/TAC.1976.1101305
- E. Fornasini and G. Marchesini, “Doubly Indexed Dynamical Systems: State-Space Models and Structural Properties,” Mathematical Systems Theory, Vol. 12, No. 1, 1978, pp. 59-72. doi:10.1007/BF01776566
- R. Gnanasekaran, “A Note on the New 1-D and 2-D Stability Theorems for Discrete Systems,” IEEE Transactions on Acoustics, Speech, & Signal Processing, Vol. 29, No. 6, 1981, pp. 1211-1212. doi:10.1109/TASSP.1981.1163695
- T. Bose and D. A. Trautman, “Two’s Complement Quantization in Two-Dimensional State-Space Digital Filters,” IEEE Transactions on Signal Processing, Vol. 40, No. 10, 1992, pp. 2589-2592. doi:10.1109/78.157299
- P. Agathoklis, E. I. Jury and M. Mansour, “Algebraic Necessary and Sufficient Conditions for the Stability of 2-D Discrete Systems,” IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 40, No. 10, 1993, pp. 251-258.
- T. Bose, “Stability of 2-D State-Space System with Overflow and Quantization,” IEEE Transactions on Circuits and Systems II, Vol. 42, No. 6, 1995, pp. 432-434. doi:10.1109/82.392319
- Y. Su and A. Bhaya, “On the Bose-Trautman Condition for Stability of Two-Dimensional Linear Systems,” IEEE Transactions on Signal Processing, Vol. 46, No. 7, 1998, pp. 2069-2070. doi:10.1109/78.700987
- T. Fernando and H. Trinh, “Lower Bounds for Stability Margin of Two-Dimensional Discrete Systems Using the MacLaurine Series,” Computer and Electrical Engineering, Vol. 25, No. 2, 1999, pp. 95-109. doi:10.1016/S0045-7906(98)00036-6
- R. Thamvichai and T. Bose, “Stability of 2-D Periodically Shift Variant Filters,” IEEE Transactions on Circuits and Systems II, Vol. 49, No. 1, 2002, pp. 61-64. doi:10.1109/82.996060
- Y. Bistritz, “Testing Stability of 2-D Discrete Systems by a Set of Real 1-D Stability Tests,” IEEE Transactions on Circuits and Systems I, Vol. 51, No. 7, 2004, pp. 1312- 1320.
- G.-D. Hu and M. Liu, “Simple Criteria for Stability of two-Dimensional Linear Systems,” IEEE Transactions on Signal Processing, Vol. 53, No. 12, 2005, pp. 4720-4723. doi:10.1109/TSP.2005.859265
- T. Kaczorek, “New Stability Tests of Positive Standard and Fractional Linear Systems,” Circuits and Systems, Vol. 2, No. 4, 2011, pp. 261-268. doi:10.4236/cs.2011.24036
- T. Liu, “Stability Analysis of Linear 2-D Systems,” Signal Processing, Vol. 88, No. 8, 2008, pp. 2078-2084. doi:10.1016/j.sigpro.2008.02.007
- E. Fornasini and G. Marchesini, “Stability Analysis of 2-D Systems,” IEEE Transactions on Circuits and Systems, Vol. 27, No. 12, 1980, pp. 1210-1217. doi:10.1109/TCS.1980.1084769
- W.-S. Lu and E. B. Lee, “Stability Analysis for TwoDimensional Systems via a Lyapunov Approach,” IEEE Transactions on Circuits and Systems, Vol. 32, No. 1, 1985, pp. 61-68. doi:10.1109/TCS.1985.1085639
- P. Agathoklis, “The Lyapunov Equation for n-Dimensional Discrete Systems,” IEEE Transactions on Circuits and Systems, Vol. 35, No. 4, 1988, pp. 448-451. doi:10.1109/31.1762
- P. Agathoklis, E. I. Jury and M. Mansour, “The DiscreteTime Strictly Bounded-Real Lemma and the Computation of Positive Definite Solutions to the 2-D Lyapunov Equation,” IEEE Transactions on Circuits and Systems, Vol. 36, No. 6, 1989, pp. 830-837. doi:10.1109/31.90402
- D. Liu and A. N. Michel, “Stability Analysis of StateSpace Realizations for Two-Dimensional Filters with Overflow Nonlinearities,” IEEE Transactions on Circuits and Systems I, Vol. 41, No. 2, 1994, pp. 127-137. doi:10.1109/81.269049
- C. Xiao, D. J. Hill and P. Agathoklis, “Stability and the Lyapunov Equation for n-Dimensional Digital Systems,” IEEE Transactions on Circuits and Systems I, Vol. 44, No. 7, 1997, pp. 614-621. doi:10.1109/81.596942
- H. Kar and V. Singh, “Stability of 2-D Systems Described by Fornasini-Marchesini First Model,” IEEE Transactions on Signal Processing, Vol. 51, No. 6, 2003, pp. 1675-1676. doi:10.1109/TSP.2003.811237
- H. Kar and V. Singh, “Stability Analysis of 2-D Digital Filters with Saturation Arithmetic: An LMI Approach,” IEEE Transactions on Signal Processing, Vol. 53, No. 6, 2005, pp. 2267-2271. doi:10.1109/TSP.2005.847857
- W.-S. Lu, “Some New Results on Stability Robustness of 2-D Digital Filters,” Multidimensional Systems and Signal Processing, Vol. 5, No. 4, 1994, pp. 345-361. doi:10.1007/BF00989278
- W.-S. Lu, “On Robust Stability of 2-D Discrete Systems,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, 1995, pp. 502-506. doi:10.1109/9.376069
- L. Xie, “LMI Approach to Output Feedback Stabilization of 2-D Discrete Systems,” International Journal of Control, Vol. 72, No. 2, 1999, pp. 97-106. doi:10.1080/002071799221262
- C. Du and L. Xie, “Stability Analysis and Stabilization of Uncertain Two-Dimensional Discrete Systems: An LMI Approach,” IEEE Transactions on Circuits and Systems I, Vol. 46, No. 11, 1999, pp. 1371-1374. doi:10.1109/81.802835
- K. Galkowski, J. Lam, S. Xu and Z. Lin, “LMI Approach to State-Feedback Stabilization of Multidimensional Systems,” International Journal of Control, Vol. 76, No. 14, 2003, pp. 1428-1436. doi:10.1080/00207170310001599113
- Z. Wang and X. Liu, “Robust Stability of Two-Dimensional Uncertain Discrete Systems,” IEEE Signal Processing Letters, Vol. 10, No. 5, 2003, pp. 133-136. doi:10.1109/LSP.2003.810754
- H. Kar and V. Singh, “Corrections to Robust Stability of Two-Dimensional Uncertain Discrete Systems,” IEEE Signal Processing Letters, Vol. 10, No. 8, 2003, p. 250. doi:10.1109/LSP.2003.816071
- X. Guan, C. Long and G. Duan, “Robust Optimal Guaranteed Cost Control for 2D Discrete Systems,” IEE Proceedings—Control Theory & Applications, Vol. 148, No. 5, 2001, pp. 355-361. doi:10.1049/ip-cta:20010596
- A. Dhawan and H. Kar, “Comment on Robust Optimal Guaranteed Cost Control for 2-D Discrete Systems,” IEE Proceedings—Control Theory & Applications, Vol. 1, No. 4, 2007, pp. 1188-1190. doi:10.1049/iet-cta:20060327
- A. Dhawan and H. Kar, “LMI-Based Criterion for the Robust Guaranteed Cost Control of 2-D Systems Described by the Fornasini-Marchesini Second Model,” Signal Processing, Vol. 87, No. 3, 2007, pp. 479-488. doi:10.1016/j.sigpro.2006.06.002
- A. Dhawan and H. Kar, “Optimal Guaranteed Cost Control of 2-D Discrete Uncertain Systems: An LMI Approach,” Signal Processing, Vol. 87, No. 12, 2007, pp. 3075-3085. doi:10.1016/j.sigpro.2007.06.001
- A. Dhawan and H. Kar, “An LMI Approach to Robust Optimal Guaranteed Cost Control of 2-D Discrete Systems Described by the Roesser Model,” Signal Processing, Vol. 90, No. 9, 2010, pp. 2648-2654. doi:10.1016/j.sigpro.2010.03.008
- A. Dhawan and H. Kar, “An Improved LMI-Based Criterion for the Design of Optimal Guaranteed Cost Controller for 2-D Discrete Uncertain Systems,” Signal Processing, Vol. 91, No. 4, 2011, pp. 1032-1035. doi:10.1016/j.sigpro.2010.07.014
- W. A. Porter and J. L. Aravena, “State Estimation in Discrete M-D Systems,” IEEE Transactions on Automatic Control, Vol. 31, No. 3, 1986, pp. 280-283. doi:10.1109/TAC.1986.1104249
- C. Du, L. Xie and Y. C. Soh, “
 Filtering of 2-D Discrete Systems,” IEEE Transactions on Signal Processing, Vol. 48, No. 6, 2000, pp. 1760-1768. doi:10.1109/78.845933
Filtering of 2-D Discrete Systems,” IEEE Transactions on Signal Processing, Vol. 48, No. 6, 2000, pp. 1760-1768. doi:10.1109/78.845933 - C. Du and L. Xie, “
 Control and Filtering of Two Dimensional Systems,” Springer-Verlag, Berlin, 2002.
Control and Filtering of Two Dimensional Systems,” Springer-Verlag, Berlin, 2002. - M. Sebek, “
 Problem of 2-D Systems,” Proceeding of the European Control Conference, Groningen, Netherlands, 28 June-1 July 1993, pp. 1476-1479.
Problem of 2-D Systems,” Proceeding of the European Control Conference, Groningen, Netherlands, 28 June-1 July 1993, pp. 1476-1479. - H. D. Tuan, P. Apkarian, T. Q. Nguyen and T. Narikiyo, “Robust Mixed
 Filtering of 2-D Systems,” IEEE Transactions on Signal Processing, Vol. 50, No. 7, 2002, pp. 1759-1771.
Filtering of 2-D Systems,” IEEE Transactions on Signal Processing, Vol. 50, No. 7, 2002, pp. 1759-1771. - L. Xie, C. Du, C. Zhang and Y. C. Soh, “
 Deconvolution Filtering of 2-D Digital Systems,” IEEE Transactions on Signal Processing Vol. 50, No. 9, 2002, pp. 2319-2331. doi:10.1109/TSP.2002.800401
Deconvolution Filtering of 2-D Digital Systems,” IEEE Transactions on Signal Processing Vol. 50, No. 9, 2002, pp. 2319-2331. doi:10.1109/TSP.2002.800401 - C. Du, L. Xie and C. Zhang, “
 Control and Robust Stabilization of Two Dimensional Systems in Roesser Models,” Automatica, Vol. 37, No. 2, 2001, pp. 205-211. doi:10.1016/S0005-1098(00)00155-2
Control and Robust Stabilization of Two Dimensional Systems in Roesser Models,” Automatica, Vol. 37, No. 2, 2001, pp. 205-211. doi:10.1016/S0005-1098(00)00155-2 - E. de Souza, L. Xie and D. F. Coutinho, “Robust Filtering for 2-D Discrete-Time Linear Systems with Convex-Bounded Parameter Uncertainty,” Automatica, Vol. 46, No. 4, 2010, pp. 673-681. doi:10.1016/j.automatica.2010.01.017
- S. Boyd, L. El Ghaoui, E. Feron and V. Balakrishnan, “Linear Matrix Inequalities in System and Control Theory,” SIAM, Philadelphia, 1994. doi:10.1137/1.9781611970777
- B. Dumitrescu, “LMI Stability Tests for the FornasiniMarchesini Model,” IEEE Transactions on Signal Processing, Vol. 56, No 8, 2008, pp. 4091-4095. doi:10.1109/TSP.2008.921768
- P. Gahinet, A. Nemirovski, A. J. Laub and M. Chilali, “LMI Control Toolbox—For Use with Matlab,” The MATH Works Inc., Natick, 1995.
- T. Hinamoto, “2-D Lyapunov Equation and Filter Design Based on the Fornasini-Marchesini Second Model,” IEEE Transactions on Circuits and Systems I, Vol. 40, No. 2, 1993, pp. 102-110. doi:10.1109/81.219824
- A. Kanellakis, “New Stability Results for 2-D Discrete Systems Based on the Fornasini-Marchesini State Space Model,” IEE Proceedings Circuits, Devices & Systems, Vol. 141, No. 5, 1994, pp. 427-432. doi:10.1049/ip-cds:19941368
- W.-S. Lu, “On a Lyapunov Approach to Stability Analysis of 2-D Digital Filters,” IEEE Transactions on Circuits and Systems I, Vol. 41, No. 10, 1994, pp. 665-669. doi:10.1109/81.329727
- T. Hinamoto, “Stability of 2-D Discrete Systems Described by Fornasini-Marchesini Second Model,” IEEE Transactions on Circuits and Systems I, Vol. 44, No. 3, 1997, pp. 254-257. doi:10.1109/81.557373
- T. Ooba, “On Stability Analysis of 2-D Systems Based on 2-D Lyapunov Matrix Inequalities,” IEEE Transactions on Circuits and Systems I, Vol. 47, No. 8, 2000, pp. 1263- 1265. doi:10.1109/81.873883
- T. Ooba, “On Stability Robustness of 2-D Systems Described by the Fornasini-Marchesini Model,” Multidimensional Systems and Signal Processing, Vol. 12, No. 1, 2001, pp. 81-88. doi:10.1023/A:1008420911857
- P. Fu, J. Chen and S.-I. Niculescu, “Generalized Eigenvalue-Based Stability Tests for 2-D Linear Systems: Necessary and Sufficient Conditions,” Automatica, Vol. 42, No. 9, 2006, pp. 1569-1576. doi:10.1016/j.automatica.2006.04.015
- T. Kaczorek, “LMI Approach to Stability of 2D Positive Systems,” Multidimensional Systems and Signal Processing, Vol. 20, No. 1, 2009, pp. 39-54. doi:10.1007/s11045-008-0050-7
- W. Paszke, J. Lam, K. Galkowski, S. Xu and Z. Lin, “Robust Stability and Stabilization of 2D Discrete StateDelayed Systems,” Systems & Control Letters, Vol. 51, No. 3-4, 2004, pp. 277-291. doi:10.1016/j.sysconle.2003.09.003
- S. Ye, W. Wang and Y. Zou, “Robust Guaranteed Cost Control for a Class of Two-Dimensional Discrete Systems with Shift-Delays,” Multidimensional Systems and Signal Processing, Vol. 20, No. 3, 2009, pp. 297-307. doi:10.1007/s11045-008-0063-2
- M. Tiwari and A. Dhawan, “Comment on ‘Robust Guaranteed Cost Control for a Class of two-Dimensional Discrete Systems with Shift-Delays’,” Multidimensional Systems and Signal Processing, 2011.

