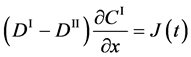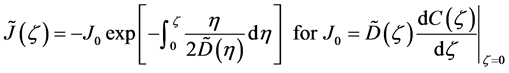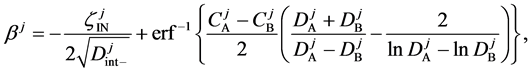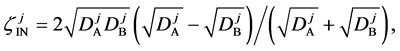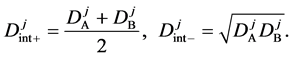Journal of Modern Physics
Vol.08 No.06(2017), Article ID:76499,16 pages
10.4236/jmp.2017.86056
Fundamental Concept of Interdiffusion Problems
Takahisa Okino1*, Hiroki Cho2, Kazu-Masa Yamada3
1Applied Mathematics Department, Faculty of Engineering, Oita University, Oita, Japan
2Department of Mechanical Systems Engineering, Faculty of Environment Engineering, University of Kitakyushu, Kitakyushu, Japan
3Department of Production Systems Engineering, National Institute of Technology Hakodate College, Hakodate, Japan

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 7, 2017; Accepted: May 21, 2017; Published: May 26, 2017
ABSTRACT
In accordance with the definition of diffusivity, the origin of coordinate system of the original diffusion equation is set at a point in the solvent material. Kirkendall revealed that Cu atoms, Zn atoms and vacancies move simultaneously in the interdiffusion region. This indicates that the original diffusion equation is a moving coordinate system for the experimentation system outside the diffusion region. The diffusion region space which means vacancies and interstices among atoms plays an important role in the diffusion phenomena. The theoretical equation of the Kirkendall effect is reasonably obtained as a shift between coordinate systems of the diffusion equation. The situation is similar to the well-known Doppler effect in the wave equation. Boltzmann transformed the original diffusion equation of a binary system into the nonlinear ordinary differential equation in accordance with the parabolic law. In the previous works, the solutions of the diffusion equation transformed by Boltzmann were analytically obtained and we found that the well-known Darken equation is mathematically wrong. In the present study, we found that the so-called intrinsic diffusivity corresponds in appearance to the physical solution obtained previously. However, the intrinsic diffusivity itself conceived in the diffusion research history is essentially nonexistent.
Keywords:
Interdiffusion, Intrinsic Diffusion, Kirkendall Effect, Parabolic Law

1. Introduction
The heat conduction equation proposed by Fourier in 1822 has been applied to investigating the temperature distribution in materials [1] . In 1855, Fick directly applied the heat conduction equation to diffusion phenomena [2] . As far as the shape of heat conduction material is unchangeable during a thermal treatment, the coordinate system of heat conduction equation set in a material is a fixed one, since the coordinate system is not influenced by the variation of internal structure in the material. Here, we should notice that the concentration of diffusion particles is a real quantity in physics, although the temperature is a thermodynamic state quantity. It is thus considered that the coordinate system of diffusion equation set in the diffusion field (solvent) is generally a moving one, since the origin of coordinate system is influenced by a variation of the diffusion field. It is thus indispensable for understanding the diffusion problems to discuss their coordinate systems, since the diffusion particles, solvent particles and also the diffusion region space which means vacancies and interstices among atoms move simultaneously against a fixed point outside the diffusion system.
When the Fick’s laws were proposed, the Gauss’s divergence theorem had been already reported in 1840 [3] . Nevertheless, the problem of coordinate system of diffusion equation was not mathematically investigated in accordance with the divergence theorem in those days. The problems of the coordinate transformation relevant to the diffusion equation had not been thus discussed in the diffusion history for a long time before the previous work [4] . The new findings, which are extremely dominant in the diffusion study, were reasonably obtained through the coordinate transformation theory then.
It seems that the new fundamental findings different from the existing diffusion theories may exert a great influence on the actual diffusion problems, just because of the fundamental findings themselves. For example, one of them reveals that the well-known intrinsic diffusion concept is unnecessary for understanding the interdiffusion phenomena [5] . However, those findings have not yet been universally known in the concerned research field [6] [7] [8] . That is the very reason to perform the present work in accordance with an entirely different viewpoint from the previous work.
The solutions of a typical interdiffusion problem were already obtained as analytical expressions in accordance with results of the well-known Boltzmann Matano method [9] [10] [11] . Using the analytical solutions for the interdiffusion problems, the fundamental problems of diffusivities and diffusion fluxes are discussed in accordance with the mathematical theory. In the present work, the original meaning of the so-called interdiffusion coefficient and that of the intrinsic diffusion coefficient misunderstood for a long time will be thus clarified in the following.
2. Raft Model of Interdiffusion Problems
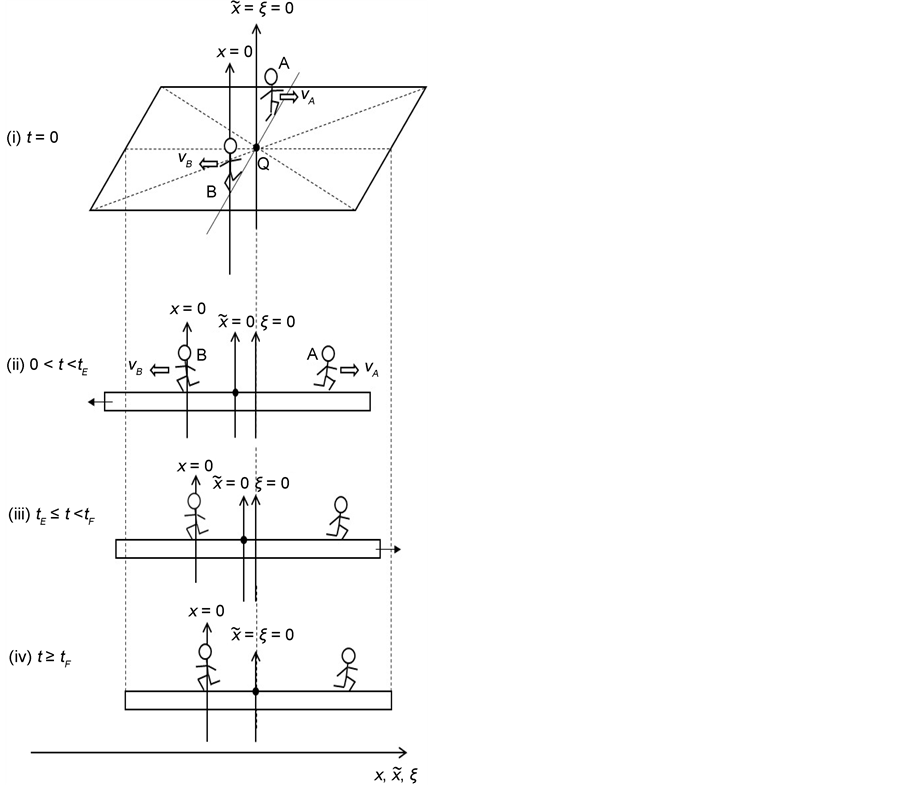
In accordance with the definition of diffusivity, the origin of coordinate system of the original diffusion equation is set at a point in the solvent material. In 1947, Kirkendall revealed that Cu atoms, Zn atoms and vacancies move simultaneously in the interdiffusion region [12] . This indicates that the original diffusion equation is a moving coordinate system for the experimentation system outside the diffusion region. A discussion on the relation between the coordinate systems of diffusion equation is indispensable for understanding diffusion phenomena [4] . Analyzing interdiffusion problems is thus considerably complicated. In the following, as an example of problems between coordinate systems, we discuss motions of persons on a raft floating on a pond before the discussion about interdiffusion problems.
The water in a pond is at rest and a rectangle raft of mass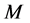 , length
, length 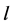 and width
and width 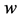 floats also at rest in the pond. As shown in Figure 1, the diagonal lines intersect each other at the point
floats also at rest in the pond. As shown in Figure 1, the diagonal lines intersect each other at the point 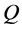 then. The origin of
then. The origin of 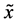 axis along the length direction is set at the point
axis along the length direction is set at the point 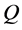 on the raft. Persons A and B with mass
on the raft. Persons A and B with mass 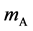 and mass
and mass 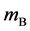 who are at rest on the line
who are at rest on the line 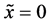 at the initial time
at the initial time 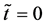
Figure 1. Raft model of interdiffusion phenomena. The persons A and B on the raft correspond to the mass center of diffusion particles and that of solvent ones. The raft and water in a pond correspond to the diffusion region space and the free space near the specimen surface of diffusion region. (i) The time 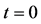 corresponds to the initial state of diffusion system. (ii) The time interval
corresponds to the initial state of diffusion system. (ii) The time interval 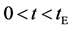 corresponds to a diffusing state at a high temperature. (iii) The time interval
corresponds to a diffusing state at a high temperature. (iii) The time interval 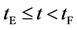 corresponds to a state of the diffusion system during temperature fall and it reaches a thermal equilibrium state at
corresponds to a state of the diffusion system during temperature fall and it reaches a thermal equilibrium state at 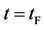 in the given room temperature. (iv) The time regions
in the given room temperature. (iv) The time regions 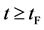 correspond to the final state after diffusion treatment.
correspond to the final state after diffusion treatment.
start walking with an arbitrary velocity for 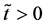 in the opposite direction from each other. Under the condition of
in the opposite direction from each other. Under the condition of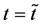 , the origin of
, the origin of 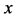

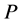
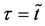



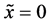
In the following, we discuss the motion of person A in the isolated system composed of the raft and persons using each of the coordinate systems, 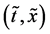
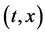
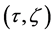

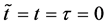
In an arbitrary time between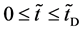
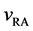

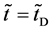
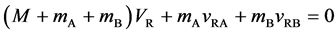
in the isolated system of the raft and persons, where 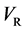
The velocities of persons A and B, 
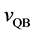
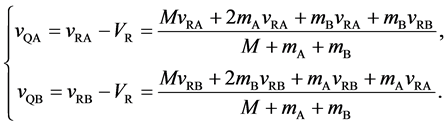
The relative velocity 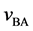
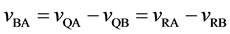
and it does not depend on the coordinate systems 

The migration length of raft between 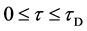
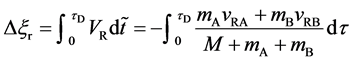
When the persons on the raft stop walking at the same time


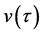
the raft returns to the initial position and it has been at rest ever since. The mass center of the isolated system is shifted from the initial state 
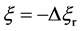
In the present model, it is thus indispensable for understanding the motion of person A against the point R to investigate the behavior of the raft and water in the pond. In other words, it is apparent that we cannot understand the motion of person A against the point R only from the relative motion between the persons A and B on the raft.
3. Binary System Interdiffusion
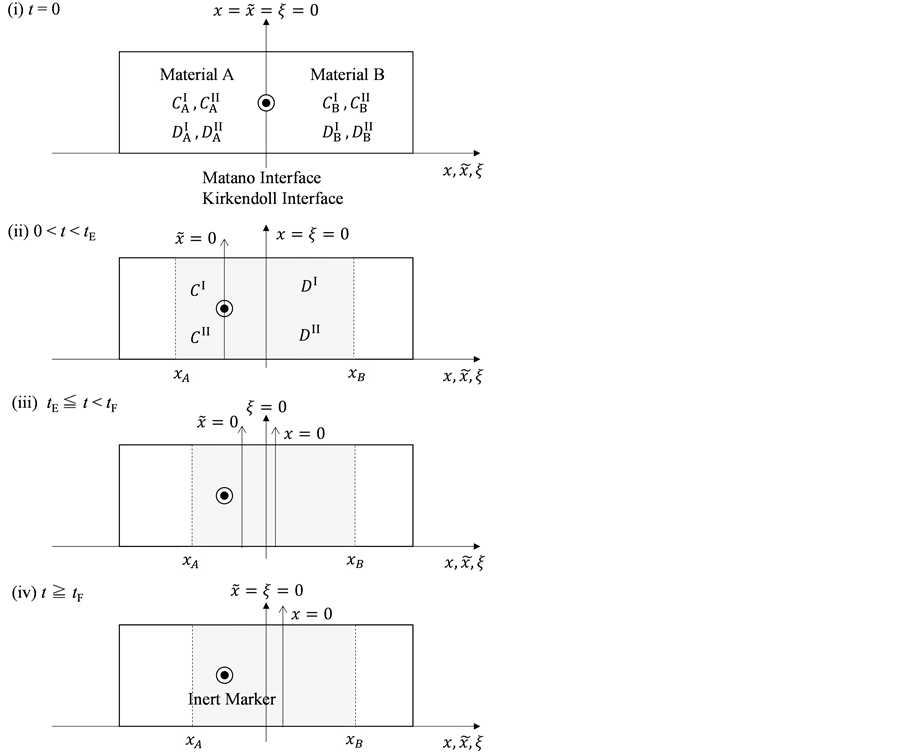
As is known from the unified theory of diffusion problems, the basic concept of diffusion phenomena is in the interdiffusion problems [4] . In the following discussion, the above raft model is reasonably applied to a typical binary system interdiffusion problem in accordance with the mathematical physics. In that case, the person A, the person B, the raft and water in the pond correspond to the mass center of diffusion particles, the mass center of solvent particles (diffusion field), the diffusion region space, and space of the diffusion region outside, respectively. Here, note that the diffusion region space and the space of diffusion region outside have no mass, whereas the raft and water in the pond have the mass 
Metal plates A and B with a uniform cross section 
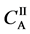
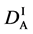
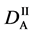


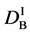

As shown in Figure 2, the diffusion couple is smoothly jointed at the interface between A and B. The coordinate axis 
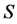
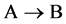
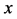
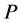

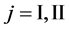

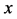

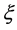
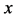
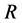
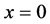
Since the diffusivity depends on an interaction between a diffusion particle and the diffusion field near the diffusion particle itself, the basic diffusion equation with the diffusivity is expressed by the time and space coordinate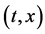
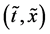


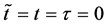
We denote the concentrations and diffusivities of I and II by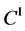

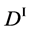
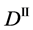
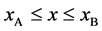
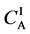
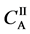
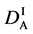

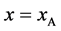

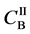



Figure 2. Typical interdiffusion problem of a diffusion couple. The metal plates A and B composed of elements I and II were used for a diffusion couple. Their diffusivities and concentrations are 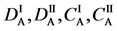
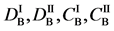
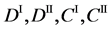
differential equations of diffusion.
The basic diffusion equations of I and II are expressed as

Since the shape variation of diffusion couple is negligible in the usual experimentation, the total particle numbers of I and II on an arbitrary cross section in the diffusion region are considered to be constant with a good approximation. In the typical interdiffusion problems, the relation of
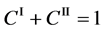
is thus generally accepted regardless of the coordinate systems, where the normalized concentrations are used.
Substituting (4) into (3) yields
and it is rewritten as
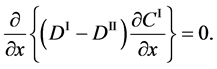
In accordance with the theory of partial differential equation, (5) means that the relation of
must be valid using an arbitrary function 
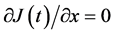
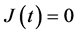
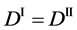

Their diffusivities are thus commonly expressed as

only in the partial differential equation (3). However, note that it is not generally valid in the actual diffusion phenomena when we substitute the initial and/or boundary values, 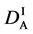
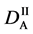
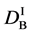
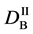
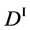
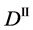
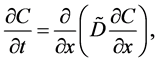
where the suffix 
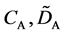
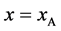
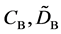
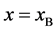
The Gauss’s divergence theory shows that the diffusion flux of basic diffusion equation (7) is obtained as
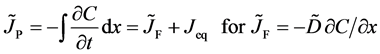
by integrating it with respect to 

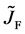

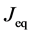
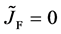
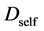

where 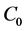
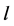
Substituting (4) into the Fickian first law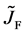
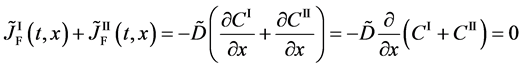
is valid only in the partial differential equation (3). Further, it is clarified that the relation of
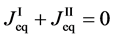
is valid in the self-diffusion theory in [4] . Equations (8), (9) and (10) yield
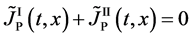
which is valid only in the partial differential equation (3).
When the origin 
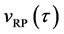
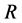
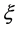
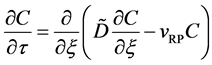
in the fixed coordinate system outside the diffusion system. Here, the relations of differential operators yielding
are used for (7), where the relations of
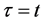
are valid between the coordinate systems 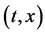
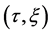
4. Solutions of Nonlinear Diffusion Equation
It is generally considered that the diffusivity 
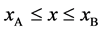
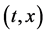
In 1894, Boltzmann transformed (7) into the nonlinear ordinary differential equation of
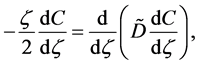
using the relation 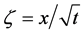
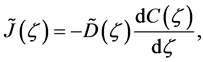
where the relation of
is used [11] [14] . Equation (14) is considered to be a diffusion flux in the parabolic space. In mathematics, that the diffusivity depends on the coordinate system yields the relation of

The general solutions of (13) were obtained as analytical expressions yielding
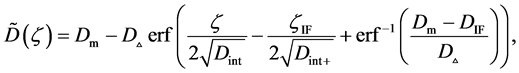
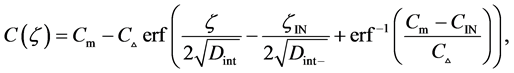
where (14) and (15) were simultaneously calculated using the integral constants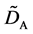
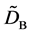
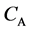
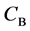
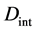
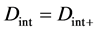
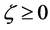

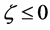
When we substitute the boundary values, 
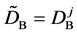
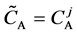
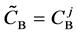
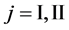
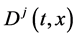
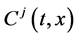

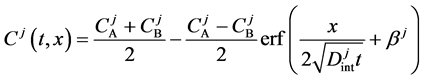
between
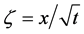
Substituting the initial and/or boundary values into the general solutions of the diffusion equation (13) i.e., (16) and (17), the physical solutions of the diffusion equation (3) were reasonably obtained as (18) and (19). As can be seen from figure 3 and figure 4 in [11] , the present solutions agree with the results of the Boltzmann Matano method. Further, it is clarified that the physical solutions of (18) and (19) are equivalent to those of (12) because of 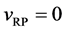
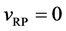
The diffusivities 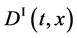
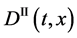
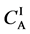
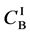
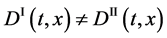
is valid between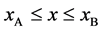
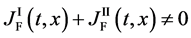
is generally valid between the diffusion fluxes obtained by using (18) and (19).
Here, note that the difference between (6) and (20) or (9) and (21) has been ignored in the diffusion history. We believe that the Kirkendall effect (K effect) is caused by the relation of (21) [12] . At the same time, as discussed later, we cannot accept the concept of intrinsic diffusion developed in the diffusion history.
In a word, the usual diffusivities 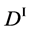



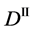
The so-called Darken equation relevant to the interdiffusion coefficient and the intrinsic diffusion coefficients has been used for analyzing interdiffusion problems for a long time [15] . However, we cannot mathematically accept the relation among the interdiffusion coefficient 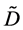
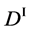
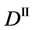
5. Flux of Diffusion Region Space
The concept of diffusion flux is useful for understanding of diffusion phenomena. The diffusion flux of the diffusion region space plays an important role to understand interdiffusion phenomena like the motion of persons in the raft model depends on the motion of raft.
The Gauss’s divergence theory shows that the diffusion flux is obtained as
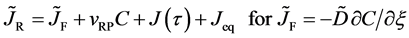
by integrating the diffusion equation (12) with respect to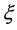

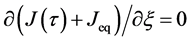
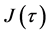
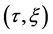
Using the velocity 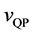
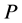

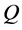
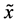
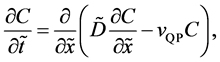
and the diffusion flux is
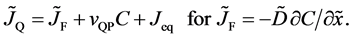
Here, note that the diffusion fluxes of (8), (22) and (24) are valid only in the partial differential equations (7), (12) and (23), respectively. When (8), (22) and (24) are applied to the elements I and II, the relation among diffusion fluxes of
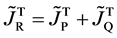
is physically valid as a relation between the inside flux of the diffusion region and the outside one, where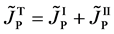
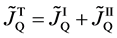
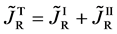
Equation (25) yields the relation of
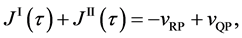
since
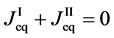
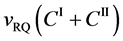

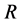

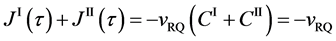
is thus valid, since the diffusion region space moves in the opposite direction against the diffusion particles.
Equations (26) and (27) yield a physically reasonable relation of
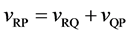
to be valid among the velocities of the coordinate systems.
6. Kirkendall Effect
In general, the diffusion experiments are performed at a high temperature between 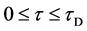
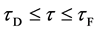
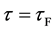

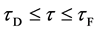
The interface 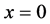
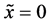
It is considered that the diffusion region is an isolated system and the mass center is immobile between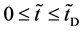
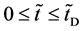

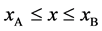
The coordinate origin set at a point P on the M interface in the initial state is also immovable, since the M interface is immovable. In other words, the relation of 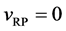
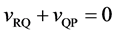
because of
Here, using the initial and/or boundary values for (24), the relation yielding
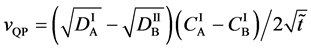
is reasonably obtained (See Appendix).
An inert marker set at the K interface moves in accordance with the flow of diffusion region space between 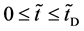

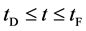
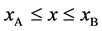
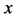
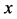
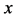
Based on the above mentioned, the migration length of an inert marker is expressed as
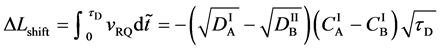
at 



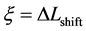
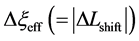
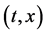
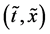
For an arbitrary time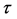
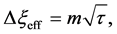
is well known, where 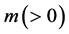
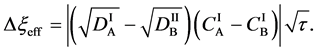
Equation (33) shows that the K effect depends not only on the initial diffusivity values but also on the initial concentration values. Here, (33) is derived by using 
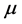

so as to agree with the empirical equation (32).
Hereinbefore, the Kirkendall effect was reasonably explained by the present interdiffusion theory, regardless of the intrinsic diffusion concept. It was thus revealed that the diffusion region space plays an important role in the interdiffusion problems. At the same time, the discussions of setting coordinate system of diffusion equation are essentially dispensable for understanding the diffusion phenomena.
7. Discussion
The diffusion study is an important subject relevant to basic problems in the fabrication process of materials such as alloys, semiconductors, functional materials, and so on. Their diffusion problems in detail have been thus widely investigated in accordance with the industrial requirement for a long time. However, some unsolved problems relevant to the fundamental nonlinear diffusion equation, which are extremely dominant in mathematical physics, have been still leaved in the diffusion history. In the cause of them, the physical interpretation of the K effect has been misunderstood for a long time.
As is well known, the physical solutions of a partial differential equation are determined from substituting the given initial and boundary values into the general solutions in mathematics. The difference between the physical solutions and the general solutions in mathematics has been confused in the diffusion history. For example, the expression of the diffusion flux 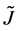
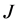
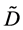
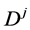
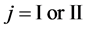
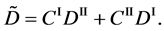
Based on the present mathematical theory, (35) is apparently wrong, since the left-hand side is a general solution whereas the right-hand is expressed by using physical solutions. Further, it is also revealed that the Darken equation is mathematically wrong in the derivation process [5] .
8. Conclusions
It had been considered for a long time that the analytical solutions of (3) are impossible. However, we could reasonably obtain the general solutions of (13) as (16) and (17). In other words, the physical solutions of (3) were analytically obtained as (18) and (19). In the present work, the fundamental concept of interdiffusion phenomena was reasonably clarified in accordance with the mathematical theory. Further, the analytical method discussed in the present work is reasonably applicable to an interdiffusion problem of many elements system [16] .
Here, the present results yield the following conclusions.
1) In general, the discussion about setting the coordinate systems of diffusion equation in the diffusion problems is essentially necessary for understanding of the diffusion phenomena.
2) An element in the interdiffusion region has only one diffusivity value. The so-called interdiffusion coefficient means the unsolved one in the partial differential equation. On the other hand, the intrinsic diffusion coefficient corresponds to the solved one using the given initial and boundary values for the general solutions. Therefore, such an especial intrinsic diffusion coefficient conceived in the diffusion history is essentially nonexistent in accordance with the mathematical theory.
In view of the influence of misunderstanding problems pointed out here on the younger, we hope that the conclusions are universally known in the concerned research field as soon as possible, just because of the fundamental matters themselves.
Cite this paper
Okino, T., Cho, H. and Yamada, K.-M. (2017) Fundamental Concept of Interdiffusion Problems. Journal of Modern Physics, 8, 903-918. https://doi.org/10.4236/jmp.2017.86056
References
- 1. Fourier, J.B.J. (1822) Analytique de la Chaleur. Didot, Paris, 499-508.
- 2. Fick, A. (1855) Philosophical Magazine, 10, 31-39.
- 3. Gauss, C.F. (1840) Resultateaus den Beobachtungen des Magnetishen Vereins, 4, 1.
- 4. Okino, T. (2015) Journal of Modern Physics, 6, 2109-2144.
https://doi.org/10.4236/jmp.2015.614217 - 5. Okino, T. (2013) Journal of Modern Physics, 4, 1495-1498.
https://doi.org/10.4236/jmp.2013.411180 - 6. Haug, K., Keiser, D. and Sohn, Y. (2013) Metallurgical and Materials Transactions A, 44, 738-746.
https://doi.org/10.1007/s11661-012-1425-9 - 7. Kuhn, P., Horbach, J., Kargl, F. and Meyer, A.Th. (2014) Physical Review B, 90, Article ID: 023409.
https://doi.org/10.1103/PhysRevA.90.023409 - 8. Paul, T.R., Belova, I.V., Levchenko, E.V., Evteev, A.V. and Murch, G.E. (2015) Diffusion Foundations, 4, 25-54.
https://doi.org/10.4028/www.scientific.net/DF.4.25 - 9. Boltzmann, L. (1894) Annual Review of Physical Chemistry, 53, 959-964.
https://doi.org/10.1002/andp.18942891315 - 10. Matano, C. (1933) Japanese Journal of Applied Physics, 8, 109-113.
- 11. Okino, T. (2011) Materials Transactions, 52, 2220-2227.
https://doi.org/10.2320/matertrans.M2011137 - 12. Smigelskas, A.D. and Kirkendall, E.O. (1947) Transactions of the Metallurgical Society of AIME, 171, 130-142.
- 13. Okino, T. (2012) Journal of Modern Physics, 3, 1388-1393.
https://doi.org/10.4236/jmp.2012.310175 - 14. Okino, T. (2012) Journal of Modern Physics, 3, 255-259.
https://doi.org/10.4236/jmp.2012.33034 - 15. Darken, L.S. (1948) Transactions of the Metallurgical Society of AIME, 175, 184-201.
- 16. Okino, T. (2014) Applied Physics Research, 6, 1-7.
https://doi.org/10.5539/apr.v6n2p1
Appendix
Even if the diffusion couple satisfies 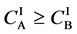

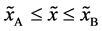
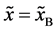
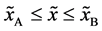

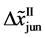

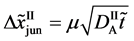
where 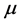

Using (A-1) and the concentration difference of boundary values

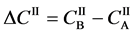
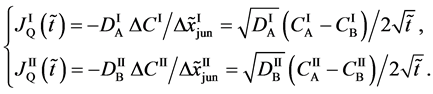
Equation (A-2) yields

The diffusion flux of (A-3) caused by the coordinate transformation corresponds to the flux of diffusion region space given by
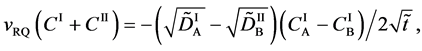
since the flux of diffusion region space moves in the opposite direction to the diffusion flux of (A-3). Substituting (A-4) into (29) yields
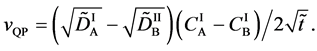
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org