ABSTRACT

By interpreting multifractal L-function zero alignment as a decoherence pro- cess, the Riemann hypothesis is demonstrated to imply the emergence of classical phase space at zero alignment. This provides a conception of emergent dynamics in which decoherence leads to classical system formation, and classical system trajectories are characterized by modular forms.

Keywords:

Riemann Hypothesis, Emergent, Phase Space, L-Functions, Modular Forms

1. Introduction

Throughout the twentieth century, a preoccupation of theoretical physics has been to identify the fundamental constitutents of matter and understand how they behave. This preoccupation has led to the construction and operation of increasingly larger particle colliders with which these constituents have been studied with greater and greater precision, and ultimately, to the discovery and validation of the Standard Model of particle physics. This model stands as a testament to the efforts of many people, and some might claim it constitutes a theory of everything once a consensus is reached on how to incorporate the gravitational force [1] .

Notably, at the root of this claim, there lies a reductionist view of the natural world, born out of extensive agreement of atomic models with experiment, and the direct observation of atoms and elementary particle tracks with scanning tunneling microscopes and particle colliders. For some, this evidence is strong enough to conclude that the Standard Model of particle physics constitutes an understanding of all biology, and even consciousness in that it describes in principle all biochemical mechanisms at an atomic level. Of course, this point of view is not universal, since scientists studying natural phenomena whose features of interest are not explained by atom-scale models may draw different conclusions, and regard such claims about human understanding as scientific overreach.

Interestingly, despite the many successes of quantum physics, there are basic theoretical questions surrounding it that remain unresolved. For instance, there is no entirely satisfactory explanation for how a measured quantum system collapses into an observable state. Secondly, though often taken for granted, it is a feature of all closed quantum systems that they undergo unitary evolution in time, because the eigenvalues of the time evolution operator are complex numbers lying on a circle of unit radius. This time evolution operator is deter- mined by the interaction and kinetic energies of a configuration of particles in space, and its success as a descriptor of atomic physical systems provides the theoretical basis for reductionism.

Given this situation, the purpose of this paper is to apply number theory to investigate the possibility that non-unitary evolution is the prime mover driving physical change. Our investigation proceeds via the study of open quantum systems which exhibit non-unitary evolution in time. From a conventional perspective, this non-unitary evolution, known as decoherence, or state mixing, is a consequence of unitary evolution of the open quantum system and its en- vironment considered as a whole. However, in this paper we’ll present a different point of view, from which quantum unitary evolution emerges as a special limit of non-unitary evolution.

In terms of layout, Chapters 2 - 4 outline research interests that motivated this work. For example, understanding how the physics of open quantum systems may be relevant to the workings of biological systems intricately coupled to their environment is discussed. Switching modes, Chapter 5 introduces the theory of solitary waves, and Chapter 6 elaborates on this discussion, introducing tau functions, modular forms and L-functions. Using these ideas, Chapter 7 introduces an alignment process analogous to state mixing that leads to the emergence of quantum unitary evolution and classical phase space, and a conjecture is made about how this emergence relates to the Standard Model. Chapter 8 concludes with a summary of results, and explains why they are of scientific interest.

2. Time and Space: Continuous or Discrete?

Classical physical theories such as electrodynamics describe physical systems as configurations of particles and fields. In these theories, a particle such as an electron or proton is idealized as a point in three dimensional space, as shown in Figure 1, and electric and magnetic fields are time dependent spatial vectors determining the direction of particle motion. For consistency with experimental observation, the real time evolution of the spatial configuration of particles and fields should obey Maxwell’s equations [2] . These equations describe a dynamic interplay between particles and fields whereby the manner in which the fields

influence particle motion and particle motion influences fields are taken into account simultaneously.

Importantly, Maxwell’s equations are differential equations describing smooth evolution of particle and field configurations in time and space. Mathematically, this relies on the assumption that time and space dimensions are coordinatized by 4 real numbers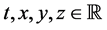. Physically, this is interesting, because it is not clear that particle motion in time and space is truly continuous. For instance, rather than being a continuum, we can imagine that time and/or space consists of a discrete lattice of points so finely placed that discontinuous motion of particles is impossible to detect. In this event, Maxwell’s equations could arise as approximations of underlying difference equations on the lattice, and we would be unable to discern the discrete quality of time and/or space.

Interestingly, this issue is not particular to classical electrodynamics, but persists generally in classical and quantum mechanical descriptions of Nature, where we can similarly imagine the differential equations describing physical systems in time and space are approximations of underlying difference equations. This situation is not entirely satisfying, because it leaves us ignorant as to whether time and space are continuous, discrete, or better understood from a different point of view.

3. Mechanics of Physical Systems

3.1. Classical Systems

In classical mechanics, a point particle constrained to move in one dimension is described by its position and momentum at any given moment in time. That is, assuming its position and momentum are coordinatized by real numbers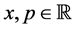, the description of its motion is given by assigning time dependence to these coordinates, making them functions and of time. Geometrically, this assignment results in time flow of the point in the plane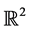. Similarly, for more complicated physical systems consisting of 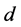point particles moving in one dimension, the collective system motion is described by the motion of a point 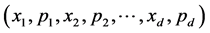in a hyperdimen- sional Euclidean space 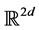parameterizing the positions and momenta of all particles in the system simultaneously. This higher dimensional space in which the entire system is treated as a single point is known as a classical phase space, and the vector field directing real time evolution of this point is known as a Hamiltonian vector field. The components of this vector field are determined by a classical Hamiltonian function defining the system’s energy [3] .

Practically speaking, classical mechanics is well equipped to model closed physical systems, but not open systems. For instance, to usefully model cell division with classical mechanics, we are forced to somewhat arbitrarily partition the phase space of the cell and its environment together into separate cell and environmental phase spaces. That is, it is necessary to identify all of the particles playing a role in the cell’s division, and model this division as a process governed by interactions between these particles and some average environmental effect. Unfortunately, this description does not allow for unpredictable variations in temperature, pressure, or particle exchange between the cell interior and exterior, making precise modeling impossible. Moreover, in the case of cell division, these sources of imprecision are complicated by the extremely large number of particles involved in all phases of the process. This situation is illustrated in Figure 2 [4] , where high resolution images of three phases of cell division are shown.

Another interesting feature of classical mechanics is that system time evolution tends to be disordered. That is, classical system trajectories are generically chaotic, filling entire -dimensional regions of the phase space, while lower dimensional trajectories expressing some degree of order are determined by Hamiltonian vector fields satisfying special symmetry constraints [5] . This is interesting, because we generally think of biological systems as maintaining a high degree of order in the presence of an ever changing environment, suggesting there may be some intricate maintenance of order inherent in the interplay between system and environmental variables that is not captured by the classical modeling approach.

Finally, as a technical point, we note that while classical physics describes the real time evolution of fields as well as particles, there is no clear choice of configuration space in which field configurations flow like there is for particles. That is, if we ask what the set of physically realizable electric field configurations across the Euclidean space 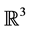is at some point in time, it is not obvious how to rigorously define this set. This is because the configuration space of the electric field is a space of functions from 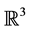to itself, and it is not obvious what mathe-

matical criteria these functions should satisfy, or how to define a probability measure on this function space as necessary to describe the statistical behavior of the field in a thermal environment.

3.2. Quantum Systems

In quantum mechanics, the Heisenberg uncertainty principle states that precise position and momentum coordinates of particles are not simultaneously specifiable. Consequently, the mathematical description of quantum particles is given in terms of position or momentum probability distribution functions, not points in phase space, and closed multi-particle systems are described by wave functions of position or momentum coordinates that evolve in time according to the dictate of a Hamiltonian energy operator rather than a Hamiltonian vector field. This operator defines real valued system energy levels, and unitary evolution of wave functions according to Schrodinger’s equation. A similar mathematical formalism describes the time evolution of quantum fields, though computations are typically performed via evaluation of Feynman diagrams rather than directly solving the Schrodinger equation. As in the case of classical mechanics, quantum mechanical modeling of biological systems with environ- mental interactions is awkward when system and environmental variables are difficult to distinguish.

One crucial difference between quantum and classical descriptions of physical systems is the effect of measurement on these systems. This difference stems from the description of quantum particles as wave functions spread out over all of position space, whereby a particle-like quality of these entities is only realized upon measurement with an experimental apparatus. The prototypical example of this is the observation of particle position on a detecting screen in Young’s double slit experiment, in which observation of classical particle-like behavior absent in the mathematical description of wave functions is referred to as wave function collapse. Intuitively, one expects collapse to be a consequence of the interaction of a quantum mechanical system with its measurement apparatus, as required to observe the system. For this reason, collapse and our experimental observation of particles is inherently related to the behavior of open quantum systems. Philosophically, this is important, because it leaves open the possibility that our classical notion of “particle” emerges from a description of open quantum systems in which this notion is not fundamental.

4. Mixing and Measuring

Turning to the study of open quantum systems, it is common to use density matrices instead of wave functions to describe system evolution, because this formalism can account for environmentally induced state transitions [6] . Typically, this evolution is described using a master’s equation derived from the Hamiltonian evolution 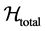of the open system and its environment together:

(1)

by averaging over environmental degrees of freedom. The upshot of this description is that most pure quantum states of the open system are unstable, and evolve into statistical mixtures of pointer states that are stable against further mixing [7] . These pointer states are clearly defined when the system and environmental interaction operators commute, in which case they are simultaneous eigenstates of these operators. However, when and do not commute, more complicated behavior results from system- environment competition. In either case, from the system’s perspective, state mixing is a non-unitary process, because it changes the information entropy of the system density matrix, unlike unitary evolution which leaves the information entropy of the density matrix constant. An illustration of an open quantum system interacting with its environment is shown in Figure 3.

As mentioned, in the commuting case, state mixing results in the off-diagonal decay of the system density matrix written in a pointer state basis. Furthermore, in the event the environment acts as a heat bath at thermal equilibrium, the diagonal weights of the density matrix evolve towards an equilibrium distribu- tion in which each pointer state is weighted by a Boltzmann factor. This process, known as relaxation, typically takes place on timescales much longer than dephasing. Figure 4 shows a rough conceptualization of the state mixing process, in which dephasing eliminates the off-diagonal elements of the density matrix, and relaxation adjusts the pointer state weights along the diagonal from to values.

Importantly, evolution of a system density matrix into a statistical mixture of pointer states is mathematically distinct from the projection of a density matrix into a pure quantum state that occurs with measurement of the system. This projection, known as collapse, has the effect of restoring a pure quantum state that can once again evolve into a mixed state upon environmental interaction. From a theoretical point of view, it is understood why measured quantum sys-

tems evolve into statistical mixtures of pointer states, because they are necessarily open to their environment. However, it is not clear how collapse into a single observable outcome occurs, and this absence of clarity lies at the heart of the measurement problem.

To obtain a classical approximation of a quantum system, the Wigner trans- form can be applied to the quantum system density matrix to construct a classical trajectory distribution on classical phase space. Depending on the mixed state represented by the density matrix, this construction is not always physically meaningful. However, in the event the density matrix represents a statistical mixture of spatially localized pointer states, applying the Wigner transform yields a time varying probability distribution on classical phase space that describes the likelihood of the system taking different classical trajectories. Conventionally, such spatially localized pointer states are called coherent states.

Remarkably, there are similarities between the theory of open quantum systems and number theory, whereby commuting and operators sharing a basis of pointer states are analogous to commuting rotation operators sharing number theoretic waveforms as eigenfunctions. Therefore, in Chapter 7 we’ll present an alignment process resembling state mixing, in which the standard time variable is replaced by a renormalization flow parameter, and pointer states are replaced by number theoretic waveforms. We’ll also see how this process leads to the emergence of quantum unitary evolution and classical phase space, and interpret classical system formation in this phase space as wave function collapse. The following two chapters provide the necessary background for this discussion.

5. Driving

To explain how the alignment process described in Chapter 7 is driven, we turn to the theory of solitary waves (i.e. solitons). This theory is useful to us because differential equations describing the motion of solitons define geometric objects called Riemann surfaces that comprise moduli spaces underlying the emergent phase space. More specifically, these moduli spaces parameterize Riemann surfaces whose real or imaginary periods vanish as they deform into modular curves, and this modular deformation is posited as the driver of multifractal zero alignment and phase space emergence.

To begin explaining this, let’s take a look at the Korteweg de-Vries (KdV) equation, the prototypical soliton equation describing non-dispersive propaga- tion of waves in shallow water [8] . This equation is the nonlinear differential equation:

(2)

where is a function describing the amplitude of the wave, and this partial differential equation can be reformulated as a Lax equation:

(3)

in differential operators and of orders 2 and 3 in:

(4)

(5)

This Lax equation has time independent solutions of the form:

(6)

where is a Weierstrass elliptic function with half periods, and these solutions can be written in terms of the 1 ´ 1 period matrix as:

(7)

(8)

or:

(9)

using the relationship between and the Jacobi theta function [9] . Remarkably, since elliptic functions are doubly periodic, by asserting, , it follows is a wave with period along the x-axis. Such a solution is shown in Figure 5 for increasing periods. In the long period limit, this periodic KdV wave becomes a soliton.

To better understand the relationship between the KdV equation and elliptic curves, let’s assume the differential operators and commute at:

(10)

In this event, according to a result of Burchnall and Chaundy, the operators and share a basis of eigenfunctions whose eigenvalues and satisfy a polynomial equation:

(11)

of degree 3 in and 2 in [10] . This polynomial defines the aforementioned elliptic curve with period matrix.

More generally, we can construct soliton equations:

(12)

solved by functions, where and are -dependent differential operators in of orders and. As before, under assumption of commutativity of and, their eigenvalues and are related by a polynomial equation of degree in and in. This polynomial defines a Riemann surface known as the spectral curve, which can be visualized as an sheeted cover of, or an sheeted cover of as shown in Figure 6. To emphasize the existence of this curve, can be replaced with, and Lax Equation (12) can be rewritten in the extended form:

(13)

in which the differential operators and depend on and, and commute at. Fixing, the solution to this equation is given by conjugation with an operator:

(14)

satisfying:

(15)

Similarly, fixing, the solution to Equation (13) is given by conjugation with an operator:

(16)

satisfying:

(17)

Because conjugation of an operator does not change its eigenvalues, the eigenvalues of the operators and in Equation (14) and Equation (16) are independent of the spectral parameters and.

Assuming the differential operators and share a single Burchnall-Chaundy (BC) eigenfunction over each point, this eigenfunction constitutes a line bundle over the spectral

curve. Moreover, since there are points distinguishing common eigenfunctions over each value of, these eigenfunctions constitute a rank vector bundle over if their linear span is independent of. Consequently, operator Equation (15) defines a connection on this vector bundle:

(18)

whose solution matrix describes the eigenfunctions of with eigenvalue. Similarly, if the span of the eigenfunctions fibered over does not change across fibers, Equation (17) gives rise to an matrix equation:

(19)

whose solution describes the eigenfunctions of with eigenvalue. Formally, Equations (18) and (19) are imaginary time Schro- dinger equations whose solutions depend on and. In Chapter 7, we’ll investigate how these solutions fibered over spectral curves deform as to define modular forms characterizing classical system trajectories. Technically, this requires introduction of a Q-deformation parameter.

To introduce these ideas, let’s imagine that a state mixing process takes place in the Q-analog limit. In this event, differential equations describing classical particle motion can emerge as limits of -difference equations, because the -difference operator acting on matrix valued functions:

(20)

defines a differentiation operator in as:

(21)

More specifically, upon substituting, the matrix -difference equation:

(22)

where is a matrix, becomes a differential equation in the parameter at whose solutions can be interpreted as the components of a vector field directing the positional change of classical particles.

Locally, -difference Equation (22) is equivalent to constant coefficient equations at and, and these local equations have solutions and with branched pole structures in the complex -plane [11] . These pole structures are shown in Figure 7 for, and consist of discrete branches stretching from 0 to together with discrete half branches stretching towards intermediary points. As, the poles on each branch flow together to form continuous branches at, in a process known as confluence.

Remarkably, these branches resemble centromeres aligning chromosomes at metaphase, as shown in Figure 2.

6. Meta-Physics

This chapter introduces tao functions, explaining their relationship to soliton equations, theta functions, and modular forms. It also provides a brief introduc- tion to L-functions and the Riemann hypothesis, as necessary for understanding the discussion in Chapter 7. Note that tao functions are more commonly known as tau functions, but the name tao, meaning great waves, has been adopted here to avoid confusion with the modular parameter.

6.1. Tao Functions

Tao functions generate solutions to soliton equations. For example, a tao function satisfying the bilinear KdV equation:

(23)

generates solutions to KdV Equation (3) via the relation:

(24)

For example, the Jacobi theta function appearing in Equation (9) is an example of a tao function solving Equation (23).

More generally, soliton equations of type (12) with have tao functions satisyfing the bilinear KdV equation that generate soliton equation solutions via logarithmic differentiation (24). Examples of time independent tao functions solving (23) are expressible in terms of Riemann theta functions:

(25)

as:

(26)

where is the genus of a spectral curve with period matrix. For fixed, this tao function maps points in to, and defines a one dimensional Schrodinger potential/operator in whose eigenvalue spectrum consists of stable bands interlaced with unstable bands [12] .

Tao functions can also be defined when, but they do not determine solutions to the KdV equation. Instead, via logarithmic differentiation, these tao functions determine solutions to the Kadomtsev-Petviashvili (KP) equation:

(27)

whenever they solve the bilinear KP equation:

(28)

Once again, Riemann theta functions provide viable examples of tao func- tions.

6.2. Modular Forms

Modular forms are functions of a modular parameter in the upper half of the complex plane satisfying:

(29)

for some discrete subgroup and weight. Typical examples of are the modular group, and the congruence subgroups, , and [13] . The set of modular forms satisfying Equation (29) for a particular group and weight is closed under addi- tion and constant multiplication, and therefore spans a complex vector space

. For, the dimension of can be calculated as:

(30)

Demonstrating that the number of independent modular forms increases with weight and level. Figure 8 shows an image of the real part of a weight modular form known as the modular discriminant.

Other examples of weight modular forms are provided by Riemann theta constants:

(31)

in which, and the 1 ´ 1 period matrix argument of the Riemann theta function is replaced by the modular parameter. These theta contants are of interest to us because they define modular functions associated with renormalization flow limits. Specifically, via its action on, the quotient group acts on a complex projective space spanned by theta constants whose ratios define weight zero modular functions on the modular curve [14] . A special case occurs when, and the ratio of two theta constants is a modular function on expressible as the ratio of two Rogers-Ramanujan modular forms in the variable:

(32)

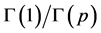
This modular function satisfies a polynomial equation whose coefficients depend on the j-invariant, and its evaluation at quadratic imaginary values of generates an algebraic extension of whose Galois group is contained in the symmetry group of the icosahedron.

In physics, modular functions arise as renormalization flow limits of Ising model partition functions [15] . To understand this, recall that the Ising energy of a one dimensional chain of spins in an external magnetic field with nearest neighbor coupling is:

(33)

Summing over all possible spin configurations, this Ising energy generates a quantum partition function:

(34)

that depends on the parameters at temperature.

Assuming the spins take values in the set, this partition function can be summed over every other spin to produce a decimated partition function satisfying:

(35)

where is a rescaling factor satisfying the transfer matrix relation [16] :

(36)

The renormalization transformation associated with this decimation and rescaling is:

(37)

(38)

and this transformation gives rise to regular and chaotic flows below and above the curve, as illustrated in Figure 9. The regular flow has stable limit points along the -axis at, and an unstable critical point at.

Formally, under repeated iteration of renormalization transformation (35), the partition function in Equation (35) may flow into a modular function of level in for some suitable function. More generally, given a one dimensional Ising model and a renormalization transformation of decimation degree acting on this model, its partition function may flow into a level modular function under repeated iteration of this transformation.

6.3. L-Functions

Artin L-functions are complex valued functions of a single complex parameter, and can be regarded as generalizations of the Riemann zeta function:

(39)

in that they are expressible as infinite products over primes. Technically, we can associate an L-function with each representation of a Galois group, where is an extension of algebraic number fields. Assuming this representation acts on a complex vector space of dimension, a unique diagonal matrix can be defined for each prime ideal unramified in the ring of integers, and these diagonal matrices determine an Artin L-function:

(40)

where is the set of singular primes that ramify in [18] .

Interestingly, it is conjectured that all non-trivial zeros of Artin L-functions lie along the critical line, as shown in Figure 10 [19] . This conjecture,

known as the generalized Riemann hypothesis, has close ties with physics. For example, it has been proposed that alignment of the Riemann zeros is related to the Hermiticity of quantum operators and/or the alignment of Yang-Lee zeros of Ising model partition functions [20] [21] . In addition, it has been conjectured that every Artin L-function equates with a Langlands L-function for some automorphic representation of an adelic group acting on a vector space of automorphic waveforms [22] . As we’ll see in the next chapter, this reciprocity conjecture is related to wave-particle duality.

7. Emergence

In this chapter, our goal is to explain how the Riemann hypothesis is related to the emergence of classical phase space, and how this emergence is driven. To this end, Figure 11 shows the zeros of a Langlands L-function stereo-

graphically projected onto the surface of a Riemann sphere. Conjecturally, these critically aligned zeros act as attractors for a multifractal L-function zero flow carrying the zeros of into the zeros of as [23] . In this chapter, we’ll assume this conjecture is true, and explain how multifractal zero flow leads to the emergence of classical phase space. Intuitively, we can think of zero flow as a state mixing process utilizing automor- phic waveforms as pointer states, and classical system formation in as wave function collapse. We can also think of zero flow as occuring with iteration of a renormalization transformation, in analogy to the way in which Yang-Lee zeros flow with renormalization of an Ising model. Because zero flow results in classical system formation at, and resembles state mixing towards pointer states acted on unitarily by commuting rotation operators, we’ll refer to it as confluent unitary mixing.

To understand the relationship between zero flow and state mixing, let’s assume the automorphic waveforms are complex valued functions:

(41)

on the adelic group acted on by via right translation. In this event, Harish-Chandra transformations of these waveforms at unramified prime places are zonal spherical (e.g. hypergeometric) functions invariant under commut- ing rotations. More specifically, zonal spherical functions are invariant under right translation by, where is a compact subgroup of whose Lie algebra of infinitesimal generators contains a rank root space. Via exponentiation, these roots generate commuting rotations sharing automorphic waveforms as eigenfunctions, and for this reason we’ll interpret them as number theoretic replacements for and operators. From this point of view, the multifractal zero flow shown in Figure 11 is a state mixing process utilizing automorphic waveforms as pointer states. To highlight this interpretation, we’ll refer to as a pointer space.

To relate multifractal zero alignment to the emergence of classical phase space, we’d like to associate zero flows with geometric objects that singularize into a classical phase space as. Unfortunately, this association is not possible for, because multifractal zero flows are transcendental in nature, and cannot be associated with phase space geometries away from zero alignment. However, with assumption of the reciprocal relation:

(42)

the Galois representation represents discrete transformations of a classical phase space on a complex vector space emerging at. A sketch of this emergence when is the 2-dimensional phase space is shown in Figure 12, in which a single hyperbolic geodesic has been indicated. This phase space is the prototypical example of a quotient space:

(43)

acted on by the discrete group, and as the quotient of a continuous group by a compact subgroup, it is a symplectic space [24] .

In the special case, represents the action of a subgroup of on a complex vector space spanned by co-cycles of, for some level. More generally, represents transformations of a -dimensional quotient space on a complex vector space spanned by of its co-cycles [25] . Physically, these co-cycles are interpretable as classical fields directing system trajectories in the phase space, and the formation of a system in is interpretable as the collapse of a measured quantum system into an observable classical phase. Importantly, because this collapse occurs in conjunction with the emergence of phase space, it also occurs in conjunction with the emergence of any spatial metric defining a conventional notion of physical distance.

Geometrically, we can understand classical system formation in using twistor theory [26] . To this end, let’s recall the setup of standard twistor theory in which twistors are complexified light rays in, and twistors intersect in pairs to form points in complexified Minkowsi spacetime. In this setup, the Penrose transform relates quantum fields over twistor space to classical fields in Minkowski spacetime, and these classical fields exhibit a geometric duality under the hodge star operator that generalizes the duality between electric and magnetic fields appearing in Maxwell’s equations. Consequently, from a twistor-centric perspective, -dimensional space- time and classical fields are not fundamental in and of themselves, but are born out of twistor incidence and twistor space geometry.

With this in mind, let’s consider a variant of twistor theory in which twistors are replaced by continuous paths in -dimensional Lagrangian (e.g. configu- ration) submanifolds:

(44)

of that intersect in pairs to form points. From this point of view, an emergent path space replaces as twistor space, replaces Minkowski spacetime as the target for twistor incidence, and co-cycles in replace Yang-Mills fields as directors of classical system trajectories. Physically, the motion of the twistor intersection point in is interpretable as instanton tunneling between a pair of quantum potential wells [27] .

Visually, we can imagine system formation in occurs with resonant splitting of a KAM torus [28] . This is shown in Figure 13-top, in which separate KAM tori split into and sub-tori, indicated as golden particles. As shown in Figure 13-middle, these particles form at points of twistor inci-

dence in a plane rotating around a central axis, and their trajectories leave and return to hyperbolic fixed points at 0 and along stable and unstable paths [29] . In return, these twistors trace dual spirals, marked in red and green, and particles traverse vortical trajectories similar to helical trajectories traversed by charged particles in static magnetic and electric fields. In Nature, dual Fibonacci spirals appear in patterns of sunflower seeds, as shown in Figure 13- bottom, in which the spiral branch ratio approximates the golden ratio.

Because the particle trajectory in Figure 13-middle is a vortex, we may suspect it has a characteristic period of rotation. In fact, up to anomalous factors, the Rogers-Ramanujan modular forms:

(45)

(46)

are Gaussian hypergeometric functions defining periods of classical rotational motion [30] . For this reason, we can imagine one of these periods characterizes the rotation of the golden particle around the central axis in Figure 13-middle. More generally, we’ll conjecture the rotational motion of the system formed in is characterized by a modular invariant tao function satisfying a differential equation of degree in. For example, may be a hypergeometric function of whose logarithmic derivative satisfies a differential equation of degree. A differential equation of this type emerges as the confluent limit of the -difference equation described in Chapter 5.

Intuitively, this conjecture is motivated by noting hypergeometric tao functions are combinatorial generating functions of signed Hurwitz numbers [31] . That is, the -coefficients of hypergeometric -series count -sheeted branched covers of the Riemann sphere, like the coverings of by the spectral curve described in Chapter 5. Consequently, for, we can think of spectral curves as points in Riemann surface moduli spaces, so in the event these moduli spaces converge into the same rank space as, emerges at as an integral over the root space underlying [32] [33] . Moreover, in the event the monodromy represen- tation of the differential equation solved by is a represention of the braid group with strands, we can picture the solutions of this differential equation as the twistor components shown in Figure 13-top. Physically, this makes sense if the logarithmic second derivatives of -point correlation functions solving the KZ differential equation define quantum potential wells between which the twistor intersection point tunnels.

To understand this in greater detail, let’s imagine Equation (18) is integrated in the complex -plane to generate a holomorphic matrix connecting and, and further imagine this holomorphic matrix is a one dimensional Ising model transfer matrix that factors:

(47)

into matrices and representing one dimensional flow and crash operators near a fixed point of the Ising model renormalization flow. Technically, this makes sense if the matrices in Equation (47) represent elements of a quantum group deforming the universal enveloping algebra of the Kac-Moody Lie algebra:

(48)

and Equation (47) is the Riemann-Hilbert factorization of along a contour encircling the origin [34] . With this assumption, the determi- nants of the flow and crash operators may be modular invariant tao functions solving Knizhnik-Zamolodchikov (KZ) differential equations whose ratio defines a modular invariant partition function [35] . For example, written as spectral determinants, the hypergeometric functions in equations (45) and (46) are tao functions of:

(49)

solving KZ differential equations, whose ratio is a unitary character of the Virasoro algebra [36] . Such characters are quantum partition functions associat- ed with unitary representations of loop groups, and conjecturally, emerge in conjunction with unitary mixing. This situation is illustrated schematically in Figure 14, in which the flow and crash operators are indicated by blue arrows, and unitary representations of loop groups emerge in conjunction with the pointer states.

Algebraically, the determinant of Riemann-Hilbert factorization (47) is a relation between scattering amplitudes in the Hopf algebra of Feynman diagrams, and in special cases, these scattering amplitudes equate with volumes of positive Grassmanniann cells [37] . For instance, this volumetric interpretation of scattering amplitudes may hold at where the Grass- mannian cells of interest are moment polytopes in the dual root space whose volumes are given by hypergeometric integrals [38] . An artistic rendering of a fan constructed by connecting the vertices of a moment polytope to a central origin is shown in Figure 15.

Interestingly, there are cases in which the the aforementioned relation between scattering amplitudes is a -difference equation. Conjecturally, this occurs when the determinant of the crash operator in Equation (47) is a function satisfying a generalization of the -difference equation:

(50)

satisfied by, that, up to anomalous factors, equates with the modular invariant tao function at. More specifically, we’ll conjecture has expression as both an infinite product and infinite sum as a consequence of generalized Rogers-Ramanujan identities, and regard the - difference equation it satisfies as a topological recursion relation describing how the root space and classical phase space emerge [39] . Furthermore, we’ll regard the root space as a moduli space of genus spectral curves whose real or imaginary periods vanish as to produce singular modular curves, because short period limits of this type create the quantum potential wells between which twistor intersection points tunnel. To emphasize the role this period vanishing plays in the emergence of phase space and characteristic modular forms, we’ll refer to it as modular deformation. A visualization of modular deformation is provided by Figure 16 using the limit set of a Fuschian group defining the spectral curve [40] .

As an example, let’s assume, , and solutions to the third degree -difference equation:

(51)

generate a modular function field of degree 3 at [14] . Explicitly, one solution to this equation is given by the infinite product:

(52)

and the ratio:

(53)

is a cyclotomic unit of degree 3 in at. This ratio does not have a continued fraction representation because -difference Equation (51) is not of degree 2, however, the ratio:

(54)

is conjectured to have a continued fraction expansion for an appropriate choice of the partition function [41] . Based on this idea, we’ll conjecture the existence of a continued fraction modular function of level p for each p > 5. We’ll also conjecture that the level 7 modular function plays a role in characterizing the electroweak force, the rank 2 gauge field in the Standard Model. Reasonable justification of this final conjecture is the subject of future work.

8. Conclusions

Blending ideas from math and physics, this paper suggests state mixing is the fundamental process underlying the time evolution of physical systems. Formally, this is achieved by replacing quantum density matrices with multifrac- tal L-functions, and the time parameter with a flow parameter that approaches zero as the zeros of a multifractal L-function align. This flow towards alignment, termed confluent unitary mixing, leads to the emergence of quantum unitary evolution and classical phase space at.

Physically, the results of this paper are of interest because they highlight a connection between open quantum systems and number theory. Specifically, commuting system and environmental interaction operators and sharing pointer eigenstates of a state mixing process are analogous to commu- ting rotation operators sharing automorphic waveforms as eigenfunc- tions. Moreover, classical system formation in the emergent phase space via twistor intersection is interpretable as the collapse of a quantum system into an observable classical phase. From this perspective, multifractal zero alignment is a phase space selection process in which and classical fields directing system trajectories are continuously changed, and Langland’s reciprocal relation is a number theoretic statement of wave-particle duality.

Mathematically, the drive towards multifractal zero alignment is explained using the theory of solitons. This is done by identifying the root space underlying as a moduli space of singular Riemann surfaces containing solitonic spectral curves whose real or imaginary periods vanish as. Using this idea, a class of modular forms characterizing classical system trajec- tories is conjectured to exist.

Outside the realm of pure science, the results of this paper may also have real world applications. For example, as described, unitary mixing instills emergent classical systems with a balance between ordered and chaotic behavior that may be relevant to understanding the presence of self organized criticality in Nature [42] . Should this prove to the case, areas of pure mathematics that have traditionally been regarded as the preoccupation of ex-centrics may find application across scientific disciplines.

Cite this paper

Brox, D. (2017) The Riemann Hypothesis and Emergent Phase Space. Journal of Modern Physics, 8, 459-482. https://doi.org/10.4236/jmp.2017.84030

References