Journal of Modern Physics
Vol.07 No.13(2016), Article ID:70398,9 pages
10.4236/jmp.2016.713148
Electron-Domain Wall Interaction with a Ferromagnetic Spherical Domain Wall
Leonardo dos Santos Lima
Departamento de Física e Matemática, Centro Federal de Educação Tecnológica de Minas Gerais, Belo Horizonte, Brazil

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 10, 2016; Accepted: September 3, 2016; Published: September 6, 2016
ABSTRACT
The interaction between an electron with a three-dimensional domain wall was investigated using the Born’s expansion of the S scattering matrix. We obtain an influence of the scattering of the electron with the ferromagnetic domain wall in the spin wave function of the electron with the aim to generate the knowledge about the state of the electron spin after the scattering. It relates to the recent problem of generation of the spin polarized electric current. We also obtain the contribution of the electron-wall domain interaction on the electric conductivity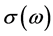 , through the wall domain, where we have obtained a peak of resonance in the conductivity for one value of
, through the wall domain, where we have obtained a peak of resonance in the conductivity for one value of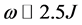 .
.
Keywords:
Electron Scattering, Domain-Wall, Ferromagnet

1. Introduction
The study of the quantum matter is an important topic of research in modern physics [1] . The description of particles interacting at low temperature is crucial in the determining and distinguishing of characteristics being an important problem in condensed matter physics. One of these problems is the study of the s − d-electron-scattering with the ferromagnetic domain wall [2] , where an electric current density crosses a ferromagnetic metallic film. The domain wall resistivity is a rather old topic and has been thoroughly studied by many research groups [3] - [5] .
The injection of a spin current in a magnetic film can generate a spin-transfer torque that acts on the magnetization collinearly to the damping torque [6] - [9] . Recently, the electron scattering by an one-dimensional domain wall in quantum wires that were described by the Luttinger liquid model was studied using Bosonization and Renormalization group [10] [11] . The transport and the scattering in quantum wires with domain wall were considered in [12] . The interaction of the domain wall with an interacting one-dimensional electron gas was studied in [13] . Peter et al. [14] have studied the influence of the domain wall scattering in the electron resistivity. Moreover, the importance to study the influence of scattering electron-domain wall is due the connection with phenomena depending on the spin such as the Giant Magneto-Resistance (GMR) [15] , where we can have a large variation of the electric resistance with the variation of magnetization through the domain wall. The Quantum information technology promises one faster and more secure means of data manipulation that makes use of the quantum properties of the matter [16] - [18] . This demands the control of the spin of the electron and the needless of filtration of the electric current. We transform an electric current spin polarized by the interaction of the spins of the electrons that compose the electric current with the spins of the wall domain, 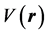 [19] - [21] .
[19] - [21] .
The model that we are interesting is described by the following Hamiltonian
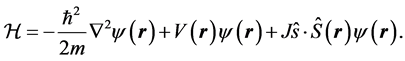 (1)
(1)
where 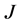 denotes the exchange interaction,
denotes the exchange interaction, 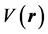 is the nonmagnetic periodic potential of the lattice and the last term
is the nonmagnetic periodic potential of the lattice and the last term 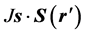 represents the potential of scattering of a electron spin with the spins of the domain wall. In an homogeneous magnetic domain wall, the magnetization is collinear,
represents the potential of scattering of a electron spin with the spins of the domain wall. In an homogeneous magnetic domain wall, the magnetization is collinear, 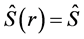 , hence it is natural to choose this direction for the axis of quantization of the spin of electron
, hence it is natural to choose this direction for the axis of quantization of the spin of electron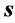 . The interaction of each electron with the spins of the wall is depicted in Figure 1. In Figure 2, we present the behavior of the potential of interaction between the spin of the electron with the spins of the wall domain.
. The interaction of each electron with the spins of the wall is depicted in Figure 1. In Figure 2, we present the behavior of the potential of interaction between the spin of the electron with the spins of the wall domain.
The purpose of this paper is to verify the influence of the scattering of electrons with the ferromagnetic domain wall on the spin wave function of the electron. We have employed the Borns approximation and the Matsubara’s Green’s function method to study the influence of the scattering of electron with the wall domain. The paper is divided in the following way. In Section 2, we discuss about the mechanism of electron scattering with the domain wall, in the Section 3, we verify the influence of electron-wall domain interaction in the current and finally, in the last section, Section 4, we present the final remarks.
2. Electron Scattering with the Domain Wall
We use the Born’s expansion of 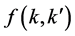 to calculate the influence of the domain wall on the spin wave function of the electron. In large distance of the wall domain, the state of the electron is given by
to calculate the influence of the domain wall on the spin wave function of the electron. In large distance of the wall domain, the state of the electron is given by
 (2)
(2)
where 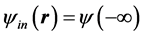 is the state of the electron after interacting with the wall. In large distance of the domain wall,
is the state of the electron after interacting with the wall. In large distance of the domain wall,  , the eigenstates
, the eigenstates 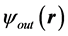 are given by
are given by
Figure 1. Interaction between one electron with the spins of the spherical domain wall of radius .
.
Figure 2. Behavior of the potential of interaction between the electron with the domain wall, 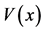 , where the width of the wall is
, where the width of the wall is

where 

as T is the transition matrix, given by the Lipmann-Schwinger’s equation

and


We consider J = 1.

as n being the number of times that the V operators enters,

and

where x' corresponds to the region of x into the ferromagnetic wall domain. We have that

where e is the electron charge and 

The integral in the Equation (12) was solved approximately using the Maple program as

where 


Such potential is plotted in Figure 2. We consider the expansion of Equation (8) in first order. An analysis considering terms of superior order will generate a large quantity of terms in Equation (13) and must not generate any change in the physics properties of the scattering.
We obtain a very complicated expression for the wave function of the electron after the scattering with the ferromagnetic wall domain however, in a combination of two polarization states. The presence of the coefficient 
3. Influence of the Spin-Domain Wall Interaction on the Conductivity
The Hamiltonian of the electron that interacts with the domain wall can be written as [22] [23]

where 





V is given by Equation (10).
Making the transformation of the spin operators



we have for the Hamiltonian

where 


We use the Matsubara’s Green function method at finite temperature [22] - [25] to determine the contribution of the interaction of the electron with the wall domain for the regular part of the electric conductivity or continuum conductivity, 

as 




where v is the Fermi’s velocity.
In Figure 3, we present the behavior of the contribution of the interaction of the electron with domain wall,



4. Conclusions and Final Remarks
In summary, we have studied the scattering between the electrons with the spherical domain wall. We have used the Born’s approximation for the S scattering matrix. We obtain a large influence of the scattering on the spin wave function of the electron. We also obtain the contribution of the electron-wall domain interaction on the electric conductivity where it is obtained a peak of resonance in the conductivity for one value of 

From a general way, it is well known that the study of the electron scattering with the
Figure 3. Behavior of the contribution of the interaction between electron with the domain-wall, 
wall domain can generate a different way to generate a spin current spin polarized based on the Hall effect of spin caused by spin-dependent scattering of electrons in thin films [6] . From an experimental point of view, recently there is an intense research about spin transport by electrons where phenomena such as the quantum Hall effect for spins and spintronic [26] - [30] have been studied extensively. In the study of these effects, often only the sign difference between related quantities like magnetic fields can generate the spin and charge currents.
Acknowledgments
This work was partially supported by the Brazilian agencies FAPEMIG, CAPES, CNPq and CEFET-MG.
Cite this paper
Lima, L.S. (2016) Electron-Domain Wall Interaction with a Ferromagnetic Spherical Domain Wall. Jour- nal of Modern Physics, 7, 1635-1643. http://dx.doi.org/10.4236/jmp.2016.713148
References
- 1. Sachdev, S. and Keimer, B. (2011) Physics Today, 64, 29.
http://dx.doi.org/10.1063/1.3554314 - 2. Berger, L. (1984) Journal of Applied Physics, 55, 1954.
http://dx.doi.org/10.1063/1.333530 - 3. Berger, L. (1992) Journal of Applied Physics, 71, 2721.
http://dx.doi.org/10.1063/1.351045 - 4. Tatara, G. and Kohno, H. (2004) Physical Review Letters, 92, 086601.
http://dx.doi.org/10.1103/PhysRevLett.92.086601 - 5. Kent, D., Yu, J., Rudiger, U. and Parkin, S. (2001) Journal of Physics: Condensed Matter, 13, R461.
http://dx.doi.org/10.1088/0953-8984/13/25/202 - 6. Berger, L. (1986) Physical Review B, 33, 1572.
http://dx.doi.org/10.1103/PhysRevB.33.1572 - 7. Slonczewski, J.C. (1996) Journal of Magnetism and Magnetic Materials, 159, L1-L7. http://dx.doi.org/10.1016/0304-8853(96)00062-5
- 8. Berger, L. (1996) Physical Review B, 54, 9353.
http://dx.doi.org/10.1103/PhysRevB.54.9353 - 9. Slavin, A. and Tiberkevich, V. (2009) IEEE Transactions on Magnetics, 45, 1875-1918.
http://dx.doi.org/10.1109/TMAG.2008.2009935 - 10. Sedlmayr, N., Eggert, S. and Sirker, J. (2011) Physical Review B, 84, 024424.
http://dx.doi.org/10.1103/PhysRevB.84.024424 - 11. Sedlmayr, N. and Berakdar, J. (2012) Physical Review B, 86, 024409.
http://dx.doi.org/10.1103/PhysRevB.86.024409 - 12. Sedlmayr, N., Ohst, J., Affleck, I., Sirker, J. and Eggert, S. (2012) Physical Review B, 86, 121302(R).
- 13. Pereira, R.G. and Miranda, E. (2004) Physical Review B, 69, 140402(R).
- 14. Levy, P.M. and Zhang, S.F. (1997) Physical Review Letters, 79, 5110.
http://dx.doi.org/10.1103/PhysRevLett.79.5110 - 15. Baibich, M.N., Broto, J.M., Fert, A., Nguyen Van Dau, F., Petroff, F., Eitenne, P., Creuzet, G., Friederich, A. and Chazelas, J. (1988) Physical Review Letters, 61, 2472.
http://dx.doi.org/10.1103/PhysRevLett.61.2472 - 16. Abdel-Aty, A.-H., Zakaria, N., Cheong, L.Y. and Metwally, N. (2014) Journal of Quantum Information Science, 4, 1-17.
http://dx.doi.org/10.4236/jqis.2014.41001 - 17. Rippard, W.H., Pufall, M.R., Kaka, S., Russek, S.E. and Silva, T.J. (2004) Physical Review Letters, 92, Article ID: 027201.
http://dx.doi.org/10.1103/PhysRevLett.92.027201 - 18. Krivorotov, L.N., Emley, N.C., Sankey, J.C., Kiselev, S.I., Ralph, D.C. and Buhrman, R.A. (2005) Science, 307, 228-231.
http://dx.doi.org/10.1126/science.1105722 - 19. Rezende, S.M., de Aguiar, F.M. and Azevedo, A. (2005) Physical Review Letters, 94, Article ID: 037202.
http://dx.doi.org/10.1103/PhysRevLett.94.037202 - 20. Pesin, D. and MacDonald, A.H. (2012) Nature Materials, 11, 409-416.
http://dx.doi.org/10.1038/nmat3305 - 21. Chumak, A.V., Vasyuchka, V.I., Serga, A.A. and Hillebrands, B. (2015) Nature Physics, 11, 453-461.
http://dx.doi.org/10.1038/nphys3347 - 22. Fradkin, E. (2013) Field Theories of Condensed Matter Physics. 2nd Edition, Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9781139015509 - 23. Wen, X.-G. (2010) Quantum Field Theory of Many-Body Systems. Oxford Graduate Texts, New York.
- 24. Kubo, R., Toda, M. and Hashitsume, N. (1985) Statistical Physics II. Springer-Verlag, New York.
http://dx.doi.org/10.1007/978-3-642-96701-6 - 25. Mahan, G.D. (1990) Many Particles Physics. Plenum, New York.
http://dx.doi.org/10.1007/978-1-4613-1469-1 - 26. Lauer, V., Bozhko, D.A., Bracher, T., Pirro, P., Vasyuchka, V.I., Serga, A.A., Jungfleisch, M.B., Agrawal, M., Kobljanskyj, Y.V., Melkov, G.A., Dubs, C., Hillebrands, B. and Chumak, A.V. (2015.) ar-Xiv:1508.07517v1
- 27. Meier, F. and Loss, D. (2003) Physical Review Letters, 90, Article ID: 167204.
- 28. Kobljanskyj, Y.V., Melkov, G.A., Serga, A.A., Slavin, A.N. and Hillebrands, B. (2015) Physical Review Applied, 4, Article ID: 014014.
http://dx.doi.org/10.1103/PhysRevApplied.4.014014 - 29. Han, W., McCreary, K.M., Pi, K., Wang, W.H., Li, Y., Wen, H., Chen, J.R. and Kawakami, R.K. (2012) Journal of Magnetism and Magnetic Materials, 324, 369-381.
http://dx.doi.org/10.1016/j.jmmm.2011.08.001 - 30. Azevedo, A., Vilela-Leao, L.H., Rodriguez-Suarez, R.L., Lacerda Santos, A.F. and Rezende, S.M. (2011) Physical Review B, 83, Article ID: 144402.
http://dx.doi.org/10.1103/PhysRevB.83.144402





