Journal of Modern Physics
Vol.07 No.06(2016), Article ID:64769,4 pages
10.4236/jmp.2016.76049
Phase Velocity and Rest Energy of Schrödinger Equation Seen from Neutrino Oscillations
Shan Zhou
School of Physics and Electrical Information, Shangqiu Normal University, Shangqiu, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 February 2016; accepted 18 March 2016; published 21 March 2016
ABSTRACT
The phase velocity is discussed using de Broglie relations and Schrödinger equation. We argue that in non-relativistic quantum mechanics the Hamiltonian should be added by a rest-energy term when Schrödinger equation is used to study the interference between particles of different masses. From neutrino oscillation experiments, we find that the phase velocity can be related to a measurable quantity (the flavor transition probability), therefore, the phase factor originated from the rest energy can’t be omitted. Correspondingly, the energy in de Broglie relations should always be total energy rather than kinetic energy, contrary to some textbooks of quantum mechanics.
Keywords:
De Broglie Relation, Phase Velocity, Neutrino Oscillation

1. Introduction
In quantum mechanics, the de Broglie relations are written as
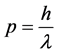 (1)
(1)
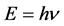 (2)
(2)
where 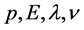 are the magnitude of momentum, energy, de Broglie wave length and frequency for a particle, and h is the Plank constant.
are the magnitude of momentum, energy, de Broglie wave length and frequency for a particle, and h is the Plank constant.
From these relations, the de Broglie wave length and frequency can be obtained for a particle with certain momentum and energy. The de Broglie wave length had already checked in the electron diffraction experiment done by Davisson and Germer in 1927. However, few experiments have checked the de Broglie frequency. The phase velocity of a particle can be obtained from the wave length and frequency using Equations (1) and (2)
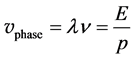 (3)
(3)
From the expressions of energy and momentum in special relativity
 (4)
(4)
where , m and
, m and 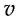 are the (rest) mass and classical propagating velocity of a particle and c is the speed of light. Therefore
are the (rest) mass and classical propagating velocity of a particle and c is the speed of light. Therefore
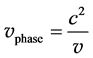 (5)
(5)
Theoretically, Equation (5) holds for particles with any velocities, including the non-relativity particles (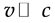 ). In some textbooks [1] - [3] , however, the energy in Equation (3) is treated as kinetic energy for a non-relativistic particle and the phase velocity is
). In some textbooks [1] - [3] , however, the energy in Equation (3) is treated as kinetic energy for a non-relativistic particle and the phase velocity is
 (6)
(6)
i.e. the phase velocity is a half of the classical propagating velocity.
Considering that the results of Equations (5) and (6) are very different especially for small velocity, it’s hard to say that, e.g. the Equation (5) is merely more accurate than Equation (6). Therefore, it is necessary to study this problem in detail.
2. Phase Velocity from Schrödinger Equation
It is usually believed that the energy in Equation (2) is the total energy rather than the kinetic energy of a particle, i.e. Equation (5) is correct, whereas Equation (6) is wrong (see Discussions). The trouble, however, is that the result of Equation (6) comes from Schrödinger equation
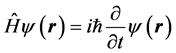 (7)
(7)
where 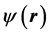 is the wave function in quantum mechanics and
is the wave function in quantum mechanics and
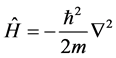 (8)
(8)
is the Hamiltonian operator for a free particle. Schrödinger equation has solutions of plane waves
 (9)
(9)
Here the normalization constant is omitted for it has nothing to do with the present work. From Equation (9), the phase velocity along direction of the momentum is obtained (the coefficient of t divided by the coefficient of r) [1]
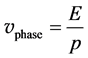 (10)
(10)
This is just the result of Equation (3). Because the energy in Schrödinger Equation is kinetic energy, which can be found out in the free particle Hamiltonian (8), the phase velocity must be calculated by Equation (6).
3. Modifying the Nonrelativistic Hamiltonian in Quantum Mechanics
In classical physics, the non-relativistic Hamiltonian can be added by a constant, which doesn’t affect the dynamics of the system, which can be simply seen from the Hamilton equation of the particles, and is usually chosen to be zero. In quantum mechanics, adding a constant to the Hamiltonian will change the wave function by a phase factor, which is unimportant for it doesn’t affect the measuring probability of any dynamical variable. On the other hand, we find that if the constant is chosen to the rest energy of a particle

Correspondingly, for low-energy particles the energy in plane wave solution (9) becomes approximately the total energy rather than kinetic energy, and the phase velocity is again obtained by Equation (5). Therefore, the uncertainty of phase velocity comes from the freedom of choosing the original point of energy, as noted in the textbook [2] .
In classical physics, the original point of energy doesn’t affect the dynamics of a system, thus it’s convenient to make it vanishing. However, the energy of a particle in quantum mechanics is related to its frequency by Equation (2), therefore, whether the original point of energy can be set to zero should be discussed in detail. On one hand, the meaning of frequency in concept is the number for something oscillating per second, thus there isn’t any freedom to choose the original point; on the other hand, if the phase difference for particles of different masses is needed, the phase factor related to the rest energy can’t be omitted. As is known to all, the phase difference for particles of different masses can cause the flavor oscillations for neutral mesons and neutrinos, thus the phase difference is related to a measurable quantity and the phase difference originate from the rest energy can’t be artificially thrown away.
4. Measurability of the Phase Velocity Seen from the Neutrino Oscillations
Take the neutrino oscillation for example, the flavor transition probability is (see e.g. [4] )

where 







refer to the total energy differences 
rest energy differences between neutrino mass eigenstates. The critical point is that the phase differences are related to a measure quantity (the transition probability), thus the phase velocity of a particle must be calculated by Equation (5) rather than Equation (6). Correspondingly, the Hamiltonian operator in Schrödinger equation should be added by a rest energy term in this case, like in Equation (11).
5. Discussions
In this paper, we clarify that the energy in de Broglie relations is the total energy of a particle, and the phase velocity must be calculated by Equation (5), whether the particle is relativistic or not. In fact, Equation (5) is well known to be correct since the formulation of the Klein-Gordon and Dirac equation. In fact, the Equation (5) has been obtained in Dirac’s textbook [5] from the relativistic formula of the Hamiltonian. As a pedagogical protocol, we suggest that in future quantum mechanical textbooks Equation (5) should always be used whether the particle is relativistic or not; on the other hand, Equation (6) should not appear to avoid the would-be misleading to students. Meanwhile, the relations of phase velocity and Schrödinger equation should be stated.
The neutrino oscillation actually should be treated in the frame of quantum field theory in order to treat the neutrino producing, propagating and detecting as a whole process. However, the quantum mechanical methods are often used to fast derive the oscillation formula without considering the producing and detecting process, because the oscillation is caused by the phase differences of different massive neutrinos originate from propagating. For the extremely relativistic neutrinos in current experiments, the motion equation should be Klein-Gordon equation or Dirac equation, thus the energy in phase factor is naturally the total energy. On the other hand, for nonrelativistic particles, e.g. the cosmic background neutrinos and the neutral K mesons, the Schrödinger equation can be used to determine the phases of the particles by simply adding a rest energy term to the Hamiltonian. On behalf of pedagogical methods, the Schrödinger equation provides us a convenient tool to elucidate the oscillation phenomenon of neutrinos and neutral mesons before studying Klein-Gordon equation and Dirac equation.
6. Conclusion
In this paper, we prove that the energy in de Broglie relation is the total energy of a particle. To mediate the contradiction between the de Broglie relation and Schrödinger equation, the Hamiltonian in Schrödinger equation should be added by a term representing the rest energy of a particle.
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grant No. 11547216 and Foundation of Henan Educational Committee under Grant No. 16A140031.
Cite this paper
ShanZhou, (2016) Phase Velocity and Rest Energy of Schrödinger Equation Seen from Neutrino Oscillations. Journal of Modern Physics,07,473-476. doi: 10.4236/jmp.2016.76049
References
- 1. Griffiths, D.J. (2009) Introduction to Quantum Mechanics. China Machine Press, Beijing. (In Chinese)
- 2. Cohen-Tannoudji, C., Diu, B. and Laloë, F. (2014) Quantum Mechanics, Vol. 1. China Higher Education Press, Beijing. (In Chinese)
- 3. Zhang, Y.D. (2008) Quantum Mechanics. Science Press, Beijing. (In Chinese)
- 4. Giunti, C. and Kim, C.W. (2001) Foundations of Physics Letters, 14, 213-229
http://dx.doi.org/10.1023/A:1012230026160 - 5. Dirac, P.A.M. (2008) The Principles of Quantum Mechanics. 4th Edition, Science Press, Beijing.

