Journal of Modern Physics
Vol.07 No.01(2016), Article ID:62612,11 pages
10.4236/jmp.2016.71003
Electron-Proton Pairing at High Temperatures, Solar Flares, and the FIP Effect
L. K. Pande1,2
1Theory Group, School of Environmental Sciences, Jawaharlal Nehru University, New Delhi, India
2C1/1206, Vasant Kunj, New Delhi, India
Email: lalit_pande@hotmail.com
Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 November 2015; accepted 3 January 2016; published 8 January 2016
ABSTRACT
We analyze the line data from solar flares to present evidence for the emission spectrum of the recently discussed electron-proton pairs at high temperatures. We also point out that since the pairing phenomenon provides an additional source for these lines―the conventional source being the highly ionized high-Z atoms already existing in the solar atmosphere, we have a plausible explanation of the FIP effect.
Keywords:
Electron-Proton Pairing at High Temperatures, Emission Spectra from Solar Flares, FIP Effect

1. Introduction
Some time back, a finite-temperature Schrodinger equation was obtained to describe the pairing of an electron and a proton in a medium of such particles at finite temperature [1] . This work was a follow-up of an earlier paper where the Coulomb potential was temperature-generalized for the first time [2] . In these papers the approach followed was somewhat intuitive, leaving open the question of a derivation from first principles. Hence, beginning with the Bethe-Salpeter equation in vacuum, such a derivation was given in [3] . In an approximation scheme, which should work at low particle densities and high temperatures, this equation gives a temperature- dependent bound state spectrum for the electron-proton pair. In the temperature range around 106 K, the deepest of the states in the spectrum have binding energies in the keV range and can withstand the background thermal agitation of the medium. The transitions from the short-lived excited states to the deepest ones in this spectrum lead to spectral lines in the soft X-ray region. An application of the approach to the flaring regions of the Sun therefore leads to the prediction of such lines in the flare spectra. In the present note, we report on this matter: the calculated lines at a certain temperature from three Balmer-like series are essentially all seen in the flare data. We also point out that, since many of these lines are identifiable with the lines which in the conventional approach are presumed to originate from the low first ionization potential (FIP) elements, our approach seems to provide an explanation of the FIP effect which has been extensively discussed in the literature, e.g., in [4] and [5] . The details are given in the following.
2. The Finite-Temperature Schrodinger Equation (FTSE) and Its Solutions
The equation for the bound state at temperature T, or the FTSE, is given by
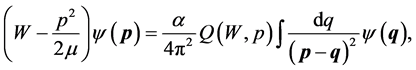 (1)
(1)
where W is the binding energy,
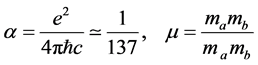 (2)
(2)
with ma and mb as the electron and the proton mass, respectively. The function Q(W, p) is given by
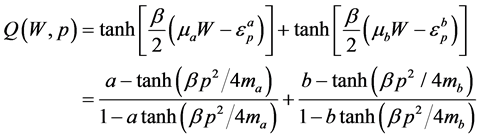 (3)
(3)
where
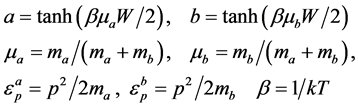 (4)
(4)
and k is the Boltzmann constant. Using the approximation
 (5)
(5)
we can write
 (6)
(6)
where
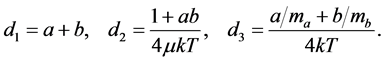 (7)
(7)
Equation (7) can be solved in this approximation to give [1]
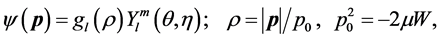
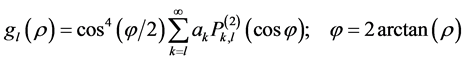 (8)
(8)
where l is the angular momentum quantum number, m the azimuthal quantum number and
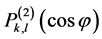 are given in terms of Gegenbauer polynomials
are given in terms of Gegenbauer polynomials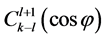 :
:
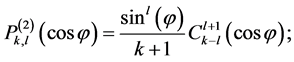 (9)
(9)
the coefficients ak in Equation (8) obey a difference equation given by
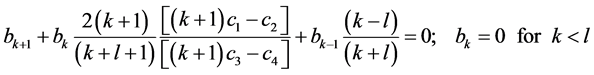 (10)
(10)
where we have put
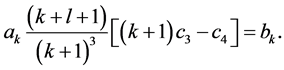 (11)
(11)
The parameters ci are given by
 (12)
(12)
Equation (10) is a second order difference equation and will in general have two solutions; the dominant and the dominated. The eigenvalues of the equation are those values of
 (or W) for which the dominant solution vanishes (for a review see [6] [7] ), and they can be computed easily by the Hill determinant method; see [8] - [10] and [1] . The generic computer program for such computations is already given in [9] , and can be adapted to the present situation without any difficulty. On substituting the numerical values for ma (electron mass), mb (proton mass) and α (the fine structure constant), we can use the program to solve for W at any given value of T. What emerges is a discrete spectrum for W: for each l, we get an increasing set of W values which can be labeled by a serial number n (which plays the role of the principal quantum number in the case of the hydrogen atom). The results are illustrated in Table 1. The typical dimensions of the Hill determinant for stability of levels up to the third decimal place (in eV) are k = 400 for n = 1, l = 0; k = 16,000 for n = 10, l = 0, k = 80,000 for n = 20, l = 0; and so on.
(or W) for which the dominant solution vanishes (for a review see [6] [7] ), and they can be computed easily by the Hill determinant method; see [8] - [10] and [1] . The generic computer program for such computations is already given in [9] , and can be adapted to the present situation without any difficulty. On substituting the numerical values for ma (electron mass), mb (proton mass) and α (the fine structure constant), we can use the program to solve for W at any given value of T. What emerges is a discrete spectrum for W: for each l, we get an increasing set of W values which can be labeled by a serial number n (which plays the role of the principal quantum number in the case of the hydrogen atom). The results are illustrated in Table 1. The typical dimensions of the Hill determinant for stability of levels up to the third decimal place (in eV) are k = 400 for n = 1, l = 0; k = 16,000 for n = 10, l = 0, k = 80,000 for n = 20, l = 0; and so on.
It is now important to make sure that the solutions obtained are indeed consistent with the approximation
given in Equation (5). This is done by verifying that the expectation values of



small. To do this, we have to first calculate.

where


Note that M in the summations S1 and S2 denotes the highest k value for which ak ≠ 0.




Table 1. Energy eigenvalues

for any given Wn,l only if the temperature T is above a certain value Tn, and furthermore, T1 > T2 > T3…etc. The relevant results are displayed in Table 2. We see from this table that the solution corresponding to W1,0 is acceptable only for T > T1 ≈ 107 K, that corresponding to W20 or W21 only for





The wavelength λ of the spectral line corresponding to any transition involving the energy difference


Substituting for any allowed

3. Application to Solar Flares
Let us now apply our approach to Solar flares. The latter are appropriate for such an application as they occur in a medium with low particle densities (≈1012/cm3) at temperatures around a few million degrees Kelvin and are known to emit soft X-ray lines. Furthermore, since the flaring phenomenon is a prolonged affair, we may expect that between the initial (growing) phase and the final (decaying) phase, there should be a period over which the flare burns at a reasonably constant temperature (with fluctuations of, say, not more than




Table 2. Temperatures for decreasing values of

Table 3. Calculated wavelength λ(Ȧ) at temperature T = 4.26 × 106 K for the emission lines comprising the generalized Balmer series A, B, and C which characterize our pair spectrum. Except for a very small difference in wavelength for the first set of lines at (3.0 → 2.1) and (3.2 → 2.1), the series A and C are degenerate. Therefore for the rest of the transitions in these series, only those from the former are given in the table. The observed wavelengths (good to within
We now turn to the relevant experimental information. The data between 5 and 20 Ȧ were obtained by Phillips et al. [13] from a flare on August 25, 1982 and from another flare on November 5, 1980. The work of Acton et al. [14] covers the range between 11 and 94 Ȧ. These observations were made on an M-class flare on July 13, 1982. They covered a much larger range of wavelengths than covered by Phillips et al., but missed out bunches of lines, especially between 12.82 and 13.45 Ȧ. McKenzie et al. [15] also provide useful data between 8 and 22 Ȧ. In the range common to all these three groups, the data of [13] are the most exhaustive. As to the accuracy of the wavelengths quoted by these authors, Acton et al. estimate it to be not better than


The experimental results in Table 3 (columns 4 and 8) are taken from Phillips et al. [13] , except in the range not covered by them, i.e., for λ(3.1 → 2.0), λ(3.0 → 2.1) and λ(3.2 → 2.1), which are from McKenzie et al. (the corresponding numbers from Acton et al. are 21.80 Ȧ and 21.60 Ȧ, not different from those of McKenzie et al. within the accuracy limit of
A look at Table 3 will show that except for the single line at λ(14.1 → 2.0) = 13.576 Ȧ [the observed wavelength closest to which is λ = 13.551 Ȧ, so that ∆λ = 0.025 which is just outside the accuracy limit of
4. Possible Connection with the FIP Effect
It may be noted that 29 distinct lines from the Solar flare data have been used up in the above as evidence for our generalized Balmer series. The data of course contain hundreds of lines over a wide range in the X-ray region. Our object is not to suggest that they all originate from our pairing mechanism. In fact, following the pioneering works of Grotrian and Edlen, we take it for granted that these lines follow from the so-called forbidden transitions in highly ionized high-Z atoms, the presence of which in stellar plasmas is a natural consequence of their having been formed in the interior of stars. The sources of a great many of these lines have accordingly been identified and the effort in that direction continues. Nevertheless, we may mention that, of the 29 lines from the data which we matched with our calculated lines, eight remain unidentified (marked [?] in Table 3) and two have questionable identification (marked [?] after the possible identification).
The conventional approach is thus not all-encompassing. In fact, the lack of proper identification in this approach of as many as eight (possibly 10) lines out of 29 does suggest that these lines may have a different origin. But what evidence could there be for such an additional origin for the other 19 lines which have been identified in the conventional approach? Interestingly enough, some evidence is indeed there. As already noted, it comes from what is called the FIP effect [4] [5] . The effect is widely observed, but we shall confine ourselves here to the part which relates to the emission lines from the Solar flares. According to conventional wisdom underlying the classical stellar atmospheres theory, the relative abundances of various elements in a star are not expected to show any variation in its upper layers (unlike in the interior where thermonuclear-process gradients exist). The relative abundance pattern for elements from the Solar photosphere should thus not be different from that obtained from the Solar flares or from the Solar coronal active regions. It turns out that this is not so. Elements with low FIP appear to be relatively more abundant in regions with T ≥ 106 K than in the photosphere (T ≈ 6000 K). How does one infer this? One compares the relative intensity pattern of emission lines for the same elements from a) the high temperature sources like the flares and the coronal active regions and b) the photosphere. One finds that the intensities of lines corresponding to the low FIP elements from the former are anomalously enhanced. This may be interpreted to mean that these low FIP elements are relatively more abundant in the high temperature sources, which is in disagreement with the classical stellar atmospheres theory. Let us now look at the situation from the point of view of this study. We observe that of the 19 lines predicted by us, which are also identifiable as lines from known elements, almost all can be traced to a single low FIP element Fe (see Table 3) in its ionized state given by Fe XIX. In the light of the FIP effect, these are thus the lines which show anomalous enhancement. Clearly, such enhancement can now be attributed to an additional mechanism for their origin viz. the pairing mechanism considered herein. Note that such enhancement will not be possible for any lines originating from the photosphere which exists at a temperature of about 6000 K at which the pairing does not take place. This opens up the possibility of leaving undisturbed the generally accepted (and empirically corroborated) picture of the uniformity of relative abundances of elements in the upper reaches of the Sun.
It may also be pointed out that the detailed theoretical calculations [16] of the intensity ratios of lines, specifically from Fe XIX, do not seem to match with the observed data from the flares. This mismatch between theory and observation may be another pointer to the existence of an additional mechanism for the origin of the above lines.
5. Conclusions
In the context of the present study, we note that the generally accepted and empirically corroborated picture of the uniformity of elements in the upper reaches of the Sun, e.g., the photosphere and the Solar flares and coronal regions, would imply that the relative intensities of spectral lines from various elements would not show any significant variation from one region to another. It turns out that this is not so. The reason is: while 19 of the 29 lines in the data analyzed here and attributed to our pairing mechanism at T = 4.26 × 106 K can also be identified with those from a single low FIP elements Fe XIX, their intensities in the flares region are found to be anomalously enhanced as compared with the intensities of lines from the photosphere. It then makes sense to conclude that this enhancement is due to the existence of another mechanism operative in the region of flares, but not in the photosphere. As has been argued above, our pairing mechanism takes place at temperatures exceeding about a million K and not at temperatures around 5000 K that characterize the photosphere. We further note that 8 (possibly 10) of the 29 lines in the data analyzed above are not identifiable (or have questionable identification) on the basis of transitions from Fe XIX or any other elements. This lends support to the view that they may well be due to the additional pairing mechanism presented here.
Finally, we should note that while a recent review [17] gives several references to the experimental data on solar flares observed since 1996, the problem of the anomalous enhancement of the abundance of elements dealt with here continues to be unaddressed. To deal with these data via the approach presented here is our next task.
Acknowledgements
The author is grateful to Dr. Bernhard Haisch for pointing out the relevance of the FIP effect to the present work. He is also grateful to Dr. J.J. Drake and Dr. Anand Bhatia for providing some valuable information. Finally, it is a matter of great pleasure to thank Dr. G.P. Malik without whose encouragement the present investigation would not have been completed.
Cite this paper
L. K.Pande,11, (2016) Electron-Proton Pairing at High Temperatures, Solar Flares, and the FIP Effect. Journal of Modern Physics,07,25-35. doi: 10.4236/jmp.2016.71003
References
- 1. Malik, G.P., Pande, L.K. and Varma, V.S. (1991) Astrophysical Journal, 379, 788-795.
http://dx.doi.org/10.1086/170554 - 2. Malik, G.P., Pande, L.K. and Varma, V.S. (1989) Pramana—Journal of Physics, 32, L89-L94.
- 3. Pande, L.K. (1991) Pramana—Journal of Physics, 37, 39-45.
- 4. Haisch, B., Julia, L., Saba, R. and Meyer, J.-P. (1996) In: Bowyer, S. and Malina, R.F., Eds., Astrophysics in the Extreme Ultraviolet, Kluwer Academic Publishers, Netherland, 511-518.
- 5. Laming, J.M., Drake, J.J. and Widing, K.G. (1995) Astrophysical Journal, 443, 416-422.
http://dx.doi.org/10.1086/175534 - 6. Hautot, A. (1986) Physical Review D, 33, 437-443.
http://dx.doi.org/10.1103/PhysRevD.33.437 - 7. Znojil, M. (1986) Physical Review D, 34, 1224-1228.
http://dx.doi.org/10.1103/PhysRevD.34.1224 - 8. Biswas, S.N., Datta, K., Saxena, R.P., Srivastava, P.K. and Varma, V.S. (1971) Physical Review D, 4, 3617-3620.
http://dx.doi.org/10.1103/PhysRevD.4.3617 - 9. Biswas, S.N., Datta, K., Saxena, R.P., Srivastava, P.K. and Varma, V.S. (1973) Journal of Mathematical Physics, 14, 1190-1195.
http://dx.doi.org/10.1063/1.1666462
http://scitation.aip.org/content/aip/journal/jmp/14/9/10.1063/1.1666462 - 10. Killingback, J.F. (1983) Microcomputer Quantum Mechanics. Adam Hilger, Bristol.
- 11. Gautschi, W. (1967) SIAM Review, 9, 24-82.
http://dx.doi.org/10.1137/1009002 - 12. Malik, G.P., Malik, U. and Varma, V.S. (1993) Astrophysics and Space Science, 199, 299-315.
http://dx.doi.org/10.1007/BF00613204 - 13. Phillips, K.J.H., Fawcett, B.C., Kent, B.J., Gabriel, A.H., Leibbacher, J.W., et al. (1982) Astrophysical Journal, 256, 774-787.
http://dx.doi.org/10.1086/159950 - 14. Acton, L.W., Bruner, M.E., Brown, W.A., Fawcett, B.C., Schweizer, W. and Speer, R.J. (1985) Astrophysical Journal, 291, 865-878.
http://dx.doi.org/10.1086/163125 - 15. McKenzie, D.L., Landecker, P.B., Broussard, R.M., Rugge, H.R., Young, R.M., Feldman, U., et al. (1980) Astrophysical Journal, 241, 409-416.
http://dx.doi.org/10.1086/158354 - 16. Bhatia, A.K., Fawcett, B.C., Lemen, J.R., Mason, H.E. and Phillips, K.J.N. (1989) Monthly Notices of Royal Astronomical Society, 240, 421-444.
http://dx.doi.org/10.1093/mnras/240.2.421 - 17. Laming, J.M. (2015) Living Rev. Solar Physics, 12, 2.
http://dx.doi.org/10.1007/lrsp-2015-2
Appendix A
We evaluate here the expectation value

where, in view of Equations (8) in the text,

and

Upon using
we obtain, after going through some elementary algebra,

With the help of the standard result

and the recurrence relation

we then get

where

Proceeding in a similar manner, we also obtain

where

We thus obtain [12]

Note that M is the summations in S1 and S2 denotes the highest k value for which ak ≠ 0, and



determinant method, which also determines the value of M. The method does not require an explicit knowledge of coefficients ak, which can be determined by using the backward Miller algorithm [12] . To this end, we define

whence Equation (10) can be written as

where

We thus have


These equations have to be supplemented by

Equation (A14a) then determines


Thus knowing Wn,l corresponding to any value of T as calculated from Equation (10), and the corresponding values of l and M, we can calculate the coefficients ak and, finally, using Equation (A10), the value of





