Journal of Modern Physics
Vol.07 No.03(2016), Article ID:63480,9 pages
10.4236/jmp.2016.73028
Invariants in Relativistic MHD Turbulence
David Garrison, Phu Nguyen
Physics Department, University of Houston Clear Lake, Houston, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 November 2015; accepted 14 February 2016; published 17 February 2016
ABSTRACT
The objective of this work is to understand how the characteristics of relativistic MHD turbulence may differ from those of nonrelativistic MHD turbulence. We accomplish this by studying the ideal invariants in the relativistic case and comparing them to what we know of nonrelativistic turbulence. Although much work has been done to understand the dynamics of nonrelativistic systems (mostly for ideal incompressible fluids), there is minimal literature explicitly describing the dynamics of relativistic MHD turbulence using numerical simulations. Many researchers simply assume that relativistic turbulence has the same invariants and obeys the same dynamics as non- relativistic systems. Our results show that this assumption may be incorrect.
Keywords:
Invariants in Relativistic MHD Turbulence

1. Introduction
Many studies in numerical relativity and high-energy astrophysics depend on the dynamics of relativistic plasmas. These include phenomena such as primordial turbulence, neutron stars, active galactic nuclei, and accretion disks near black holes [1] -[8] . Unfortunately, we do not know if the results of these studies are accurate because of approximations such as the use of nonrelativistic fluid dynamics and the lack of a standard model to describe the dynamics of relativistic turbulence. In particular, very little is understood about the turbulent dynamics of a relativistic plasma or its effect on the evolution of magnetic fields. This can only effectively be studied through direct numerical simulation of the relativistic magnetofluid.
In the following report we will first discuss what is currently known about the dynamics of nonrelativistic MHD systems. We introduce the standard incompressible and compressible nonrelativistic MHD evolution equations as well as the ideal invariants for those systems. In Section 4, we will introduce the relativistic MHD equations and the relativistic equivalents of the nonrelativistic ideal MHD invariants. We then describe our numerical experiment and present our results for a relativistic MHD code. We conclude by discussing the similarities and differences between the different systems.
2. Nonrelativistic Incompressible MHD
Work by Shebalin [9] -[14] , on ideal homogeneous incompressible MHD turbulence best demonstrates how the dynamics of a magnetofluid can differ from that of a hydrodynamic fluid. Plasma can be accurately modeled as a fluid made up of charged particles that are therefore affected by magnetic fields as well as particle-particle interactions. Because of this, the magnetic field becomes a dynamic variable in addition to density, pressure and the velocity of particles. For example, In MHD turbulence, an equipartition occurs and we expect kinetic and magnetic energy fluctuations to become roughly equal. Shebalin modeled the magnetofluid as a homogenous system where the same statistics are considered valid everywhere in the computational domain. He utilized periodic boundary conditions and spectral methods in order to study how the dynamics of different scales interacted without the addition of boundary errors. Much of his work focused on an ideal MHD system, where the magnetic and fluid dissipation terms were excluded. Below are the evolution equations used by Shebalin to describe the incompressible MHD system.
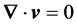 (1a)
(1a)
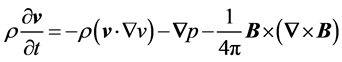 (1b)
(1b)
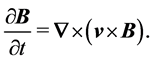 (1c)
(1c)
By varying the mean magnetic field (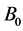 ) and angular velocity (
) and angular velocity (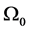 ) of the system, Shebalin was able to define five different cases with different invariants as shown in Table 1. In such a system there could be as many as 3 ideal invariants; energy (E), and the psuedoscalars cross helicity (
) of the system, Shebalin was able to define five different cases with different invariants as shown in Table 1. In such a system there could be as many as 3 ideal invariants; energy (E), and the psuedoscalars cross helicity ( ) and magnetic helicity (
) and magnetic helicity (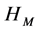 ). In addition, the invariant parallel helicity,
). In addition, the invariant parallel helicity, 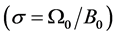
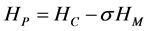 , can be formed from a linear combination of cross and magnetic helicity. In a hydrodynamic fluid the ideal invariants are only energy and kinetic helicity.
, can be formed from a linear combination of cross and magnetic helicity. In a hydrodynamic fluid the ideal invariants are only energy and kinetic helicity.
For an incompressible fluid u(k, t) is the Fourier coefficient of turbulent velocity and b(k, t) is the Fourier coefficient of the turbulent magnetic field. The energy, cross helicity and magnetic helicity can be expressed in terms of these as:
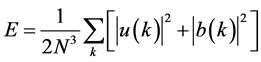 (2a)
(2a)
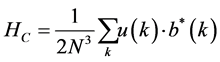 (2b)
(2b)
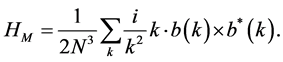 (2c)
(2c)
A cubic computational domain with N grid points in each direction is assumed. The statistical mechanics of the system is defined by the Gaussian canonical probability density function (PDF):
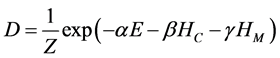 (3a)
(3a)
Table 1. Invariants for ideal incompressible MHD.
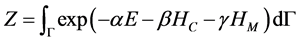 (3b)
(3b)

where Z is the partition function and 

averages using the PDF while 


it is non-ergodic. Here




be found as a function of



Phase portraits resulting from computer simulations of Shebalin’s five cases show that coherent structures formed in many systems where the magnetofluid was experiencing turbulence [9] -[14] . Coherent structure occurs when time-averaged physical variables in MHD turbulence have large mean values, rather than the zero mean values expected from theoretical ensemble predictions. MHD turbulence thus has broken ergodicity, which can be explained by finding the eigenmodes of the system. One out of the four eigenvalues associated with each of the lowest wavenumbers will be very much smaller than the others; the eigenvariables associated with these very small eigenvalues grow to have very large energies compared to other eigenvariables; when this happens, an almost force-free state occurs in which large-energy eigenmodes are quasistationary while low- energy eigenmodes remain turbulent; thus, the predicted ergodicity has been dynamically broken. This is observed to occur even in dissipative systems because broken ergodicity in MHD turbulence manifests itself at the smallest wavenumbers (largest length scales) where dissipation is negligible, resulting in the ideal spectrum. In the case of ideal hydrodynamic turbulence, broken ergodicity can occur in a finite model system, but only at the largest wavenumbers (smallest scales). When dissipation is added, the large wavenumber modes are most affected and their energy quickly decays away, so that broken ergodicity plays no role in decaying hydrodynamic turbulence.
3. Nonrelativistic Compressible MHD
Compressible MHD systems have not been studied as much as incompressible systems so here we will focus primarily on their invariants. We will assume that both incompressible and compressible systems share the same statistical mechanics and dynamics whenever the same invariants apply. In a nonrelativistic compressible MHD system; Energy and the Incompressible form of Cross Helicity are always conserved for a nondissipative system [15] -[17] (see Table 2). Compressible Cross Helicity, 
Given that our relativistic system is by default a compressible system, we naively expect to see that the same ideal invariants will apply for the relativistic system as the nonrelativistic compressible system. The equations for ideal compressible MHD are similar to those of the incompressible system with the exception of the first equation.

Table 2. Invariants for ideal compressible MHD.


4. Relativistic MHD Systems
The fluid and electromagnetic components of the relativistic MHD equations are developed from several well-known equations [32] . They include the conservation of particle number, the continuity equation, the conservation of energy-momentum, the magnetic constraint equation and the magnetic induction equation. For a system consisting of a perfect fluid and an electromagnetic field, the ideal MHD stress-energy tensor is given by






Here, P is the fluid pressure, 




terms of the energy density using the 


and 




Here, 









Notice that unlike the nonrelativistic system, we use the stress-energy tensor within the evolution equations so that 4-momentum conservation is built into the system. This results in a set of equations that look very different from that of the nonrelativistic system. According to work by Yoshida [33] [34] , in addition to 4-momentum, relativistic systems are expected to conserve a quantity called Relativistic Helicity. It is defined below using the canonical 4-momentum density, 

Here the canonical 4-momentum density 




5. Methodology
For this numerical experiment, we calculate Energy Density (E), Relativistic Helicity Density (








Here the magnetic field is related to the vector potential by the equation,





In order to study the invariants of the relativistic MHD equations, we used a code called FixedCosmo which was originally written by one of us [4] to study the dynamics of primordial plasma turbulence. This code was developed using the open source Cactus framework (www.cactuscode.org). Cactus was originally developed to perform numerical relativistic simulations of colliding black holes but it’s modular design has since allowed it to be used for a variety of Physics, Engineering and Computer Science applications. It is currently being maintained by the Center for Computation and Technology at Louisiana Sate University. Cactus codes are composed of a flesh (which provides the framework) and the thorns (which provide the physics). FixedCosmo is a collection of thorns. It uses the form of the Relativistic MHD equations described by Duez [32] and is written in a combination of F77, F90, C and C++. This code is parallelized and capable of using several different differencing methods such as second order finite differencing, fourth order finite differencing and spectral differencing. Although the code is capable of utilizing artificial viscosity and HRSC, neither was used for this project.
Because the objective of this study is to test the ideal relativistic MHD system, we complete a series of runs in a “high-energy” regime. The parameters used approximate that of the early universe around the electroweak scale. This is done so we can apply the results to any relativistic MHD system. Table 3 shows a matrix of the test runs.
Each data run utilized Fourier spectral differencing on a grid with 64 × 64 × 64 internal data points. We ran these simulations for about 7500 iterations or over 10−9 s of physical time. The electron oscillation time for the “high energy” regime is about 

6. Results
Truncation errors were found by doubling the resolution and measuring the change in the observed total errors. By assuming that the Euler Method, used to calculate

If the truncation errors are within an order of magnitude of the normalized errors, we can conclude that the system is invariant. We also found it impossible to completely eliminate the mean magnetic field and mean angular momentum in all cases. A mean magnetic field (on the order of 1% of the maximum field) remained in every case. Also, each case seemed to have a small angular velocity, also less than 1% of the fluid velocities within the simulation. The authors feel that these residual quantities where not enough to significantly disrupt the system and could be safely ignored.
Table 3. High energy numerical simulations.
Table 4. High energy simulation results.
The results in Table 4 were calculated by averaging the absolute values of normalized errors. As one can see, Energy and Relativistic Helicity appear to be conserved in every case given that the normalized error appears to be dominated by truncation errors for both. Cross Helicity may be conserved in every case since the calculated truncation error appears to be within an order of normalized errors in every case. Magnetic Helicity does not appear to be conserved in any of the cases. Normalized Errors for Cross Helicity Conservation appear smaller in cases where a large mean angular velocity is present. Deviations in Magnetic Helicity Conservation are smallest in the absence of a large mean magnetic field.
7. Discussion
Our results show that in the high-energy Relativistic MHD regime only Energy and Relativistic Helicity are clearly conserved. We are not able to conclusively prove Cross Helicity conservation. Magnetic Helicity conservation is questionable in this system. This is not an unexpected result but it does raise several interesting questions which lie beyond the scope of this article. Does the potential lack of Cross and Magnetic Helicity Conservation effect the dynamics of the relativistic system when it comes to phenomena such as inverse Energy Cascade or the Kolmogorov Energy Spectrum? How do magnetic dynamos in relativistic MHD systems function? Are there any other overlooked dynamics in relativistic MHD systems? These are all questions which we hope to address in future numerical studies.
Conflicts of Interests
The authors declare that there is no conflict of interests regarding the publication of this article.
Acknowledgements
The authors would like to acknowledge the support of the University of Houston Center for Advanced Computing and Data Systems for access to the high performance computing resources used for the completion of this project. The authors would also like to thank John Shebalin for several useful conversations and helpful suggestions.
Cite this paper
DavidGarrison,PhuNguyen, (2016) Invariants in Relativistic MHD Turbulence. Journal of Modern Physics,07,281-289. doi: 10.4236/jmp.2016.73028
References
- 1. Caprini, C. and Durrer, R. (2006) Physical Review D, 74, Article ID: 063521.
- 2. Caprini, C., Durrer, R. and Servant, G. (2009) Journal of Cosmology and Astroparticle Physics, 912, 24.
http://dx.doi.org/10.1088/1475-7516/2009/12/024 - 3. Cho, J. (2006) Journal of the Korean Physical Society, 49, 4.
- 4. Garrison, D. (2014) Journal of Gravity, 2014, Article ID: 407197.
- 5. Inoue, T., Asano, K. and Ioka, K. (2011) Astrophysical Journal, 734, 77.
http://dx.doi.org/10.1088/0004-637X/734/2/77 - 6. Melatos, A. and Peralta, C. (2010) Astrophysical Journal, 709, 77.
http://dx.doi.org/10.1088/0004-637X/709/1/77 - 7. Zhang, W., MacFadyen, A. and Wang, P. (2009) Three-Dimensional Relativistic MHD Simulations of the Kelvin-Helmholtz Instability: Magnetic Field Amplification by a Turbulent Dynamo.
- 8. Zrake, J. and MacFadyen, A. (2011) Numerical Simulations of Driven Relativistic MHD Turbulence.
- 9. Shebalin, J.V. and Montgomery, D. (1988) Journal of Plasma Physics, 39, 339-367.
http://dx.doi.org/10.1017/S0022377800013076 - 10. Shebalin, J.V. (2002) The Statistical Mechanics of Ideal Homogeneous Turbulence. NASA TP-2002-210783.
- 11. Shebalin, J.V. (2005) Discrete & Continuous Dynamical Systems B, 5, 153-175.
http://dx.doi.org/10.3934/dcdsb.2005.5.153 - 12. Shebalin, J.V. (2007) Physics of Plasmas, 14, Article ID: 102301.
http://dx.doi.org/10.1063/1.2780138 - 13. Shebalin, J.V. (2011) Geophysical and Astrophysical Fluid Dynamics, 107, 411-466.
http://dx.doi.org/10.1080/03091929.2011.589385 - 14. Shebalin, J.V. (2012) Geophysical and Astrophysical Fluid Dynamics, 107, 353-375.
http://dx.doi.org/10.1080/03091929.2012.689299 - 15. Banerjee, S. (2014) Compressible Turbulence in Space and Astrophysical Plasmas: Analytical Approach and in Situ Data Analysis for the Solar Wind. Dissertation, Université Paris Sud (Paris XI), Paris.
- 16. Marsch, E. and Mangeney, A. (1987) Journal of Geophysical Research, 92, 7363-7367.
http://dx.doi.org/10.1029/JA092iA07p07363 - 17. Yokoi, N. (2013) Geophysical & Astrophysical Fluid Dynamics, 107, 114-184.
http://dx.doi.org/10.1080/03091929.2012.754022 - 18. Biskamp, D. (2003) Magnetohydrodynamic Turbulence. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511535222 - 19. Cho, J. (2005) The Astrophysical Journal, 621, 324-327.
http://dx.doi.org/10.1086/427493 - 20. Dolgov, A.D., Grasso, D. and Nicolis, A. (2002) Physical Review D, 66, Article ID: 103505.
http://dx.doi.org/10.1103/PhysRevD.66.103505
http://arxiv.org/abs/astro-ph/0206461 - 21. Ghosh, S., Stribling, W.T., Goldstein, M.L. and Matthaeus, W.H. (1995) The Evolution of Magnetic Helicity in Compressible Magnetohydrodynamics with a Mean Magnetic Field. In: Ashour-Abdalla, M., Chang, T. and Dusenbery, P., Eds., Space Plasmas: Coupling between Small and Medium Scale Processes, American Geophysical Union, Washington DC.
- 22. Gogoberidze, G., Kahniashvili, T. and Kosowsky, A. (2007) Physical Review D, 76, Article ID: 083002.
http://dx.doi.org/10.1103/PhysRevD.76.083002
http://arxiv.org/abs/0705.1733 - 23. Islam, J.N. (1992) An Introduction to Mathematical Cosmology. Cambridge University Press, Cambridge.
- 24. Kahniashvili, T. (2005) Gravitational Radiation from Primordial Helical Turbulence.
http://arxiv.org/abs/astro-ph/0508459 - 25. Kahniashvili, T., Gogoberidze, G. and Ratra, B. (2005) Physical Review Letters, 95, Article ID: 151301.
http://arxiv.org/abs/astro-ph/0505628
http://dx.doi.org/10.1103/PhysRevLett.95.151301 - 26. Kahniashvili, T. and Ratra, B. (2007) Physical Review D, 75, Article ID: 023002.
http://arxiv.org/abs/astro-ph/0611247
http://dx.doi.org/10.1103/PhysRevD.75.023002 - 27. Kahniashvili, T., Kosowsky, A., Gogoberidze, G. and Maravin, Y. (2008) Physical Review D, 78, Article ID: 043003.
http://arxiv.org/abs/0806.0293
http://dx.doi.org/10.1103/PhysRevD.78.043003 - 28. Kahniashvili, T., Campanelli, L., Gogoberidze, G., Maravin, Y. and Ratra, B. (2008) Physical Review D, 78, Article ID: 123006.
http://dx.doi.org/10.1103/PhysRevD.78.123006
http://arxiv.org/abs/0809.1899 - 29. Kahniashvili, T., Kisslinger, L. and Stevens, T. (2010) Physical Review D, 81, Article ID: 023004.
http://arxiv.org/abs/0905.0643
http://dx.doi.org/10.1103/PhysRevD.81.023004 - 30. Kisslinger, L.S. (2004) Modern Physics Letters A, 19, 1179-1186.
http://arxiv.org/abs/hep-ph/0402001
http://dx.doi.org/10.1142/S0217732304014537 - 31. Nicolis, A. (2004) Classical and Quantum Gravity, 21, L27-L33. http://arxiv.org/abs/gr-qc/0303084
http://dx.doi.org/10.1088/0264-9381/21/4/L05 - 32. Duez, M.D., Liu, Y.T., Shapiro, S.T. and Stephens, B.C. (2005) Physical Review D, 72, Article ID: 024028.
http://arxiv.org/abs/astro-ph/0503420v2
http://dx.doi.org/10.1103/PhysRevD.72.024028 - 33. Yoshida, Z., Kawazura, Y. and Yokoyama, T. (2014) Journal of Mathematical Physics, 55, Article ID: 043101.
http://dx.doi.org/10.1063/1.4872236 - 34. Kawazura, Y., Yoshida, Z. and Fukumoto, Y. (2014) Journal of Physics A: Mathematical and Theoretical, 47, Article ID: 465501.
http://dx.doi.org/10.1088/1751-8113/47/46/465501


