Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60371,8 pages
10.4236/jmp.2015.613180
Ab-Initio Calculations of 27 Electronic States of the BP+ Ion-Molecule
Mahdi Mansour1, Nayla El-Kork2, Mahmoud Korek1*
1Faculty of Science, Beirut Arab University, Beirut, Lebanon
2Khalifa University, Sharjah, United Arab Emirates
Email: *fkorek@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 August 2015; accepted 14 October 2015; published 19 October 2015
ABSTRACT
The theoretical investigation of the potential energy curves, in the representation 2s+1Λ(+/−), of the 27 low-lying Doublet and Quartet electronic states of the BP+ molecular ion has been performed with the methods in quantum chemistry, the Complete Active Space Self Consistent Field (CASSCF) and the Multireference Configuration Interaction (MRCI) calculations. The harmonic vibrational frequency ωe, the inter-nuclear distance at equilibrium Re, the rotational constant Be, the electronic energy with respect to the minimum ground state energy Te, and the permanent dipole moment have also been calculated. Twenty-three new electronic states have been investigated here for the first time. The comparison between the values of the present work and those available in the literature for several electronic states shows a good agreement. These investigated data can be a conducive to further work on BP+ molecular ion in both experimental and theoretical research.
Keywords:
Ab Initio Calculation, Electronic Structure, Spectroscopic Constants, Potential Energy Curves, Dipole Moments

1. Introduction
The theoretical calculations and potential energy function of diatomic molecules have been one of several molecular physics important researches [1] . Although a solid description of molecular properties of molecular potential energy function is approximated at Born-Oppenheimer, it remains important for the analysis of dissociation and stability [2] . In 1972, Gingerich and Piacente [3] only studied the dissociation energy of BP molecule by means of Knudsen cell mass spectrometry; they measured the dissociation energy
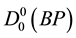 = 82.0 & 4 kcal mol−l or, and 0 K was used as the reference temperature, but they did not give other experimental data on the BP radical. BP+ ion-molecule, attracted much attention as refractory semiconductor due to its physical and chemical properties [4] -[11] . Linguerri et al. [11] found that the ground state of BP+ was X4Σ− and they determined their spectroscopic constants Te, Re, ωe, ωeχe and Be for the first time by using MRCI calculations. The physical properties of BP+ took less attention than the BP molecule [6] -[9] , but recently the ground state and the lowest excited state of BP+ ion-molecule acquired much focus. Multi-reference configuration interaction method was applied by Guo et al. [12] to investigate the BP+ ground and the lowest 5 excited electronic states.
= 82.0 & 4 kcal mol−l or, and 0 K was used as the reference temperature, but they did not give other experimental data on the BP radical. BP+ ion-molecule, attracted much attention as refractory semiconductor due to its physical and chemical properties [4] -[11] . Linguerri et al. [11] found that the ground state of BP+ was X4Σ− and they determined their spectroscopic constants Te, Re, ωe, ωeχe and Be for the first time by using MRCI calculations. The physical properties of BP+ took less attention than the BP molecule [6] -[9] , but recently the ground state and the lowest excited state of BP+ ion-molecule acquired much focus. Multi-reference configuration interaction method was applied by Guo et al. [12] to investigate the BP+ ground and the lowest 5 excited electronic states.
The present work is devoted to an accurate description of the ground and electronically 26 excited doublet and quartet electronic states. In order to emphasize the accuracy of our work we used the multi-reference configuration interaction (MRCI+Q) model expansion. The potential energy curves, the spectroscopic constants Re, Te, Be, and ωe for each of the corresponding electronic states have been investigated along with their static dipole moment.
2. Method of Calculations
The Hartree-Fock method relies on averages; it does not consider the instantaneous electrostatic interactions between electrons, nor does it take into account the quantum mechanical effects on electron distributions because the effect of n-1 electrons, on an electron of interest, is treated in an average way. This method ignores the electron correlation which is the difference in energy between the HF and the lowest possible energy.
A singly, doubly, triply, quadruply, …, N-tuply excited states is called a Configuration State Function (CSF). The exact ground and excited-states wavefuntions can be expressed as a linear combination of all possible N- electron Slater determinants arising from a complete set of spin orbitals
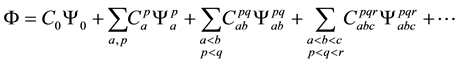
where all the C’s are expansion coefficients that must converge to zero and this method is called Configuration Interaction (CI). A simple formula known as the Davidson Correction has been proposed for estimating the contribution ΔEQ of quadruply excited determinants to the correlation energy
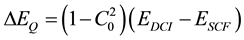
The development of efficient multiconfiguration self-consistent field method MCSCF is particularly important for excited states. One such scheme is the Complete Active-Apace Self-Consistent Field method (CASSCF). In this approach, the spinorbitals are divided into three classes: 1) set of inactive orbitals composed of the lowest energy spinorbitals which are doubly occupied in all determinants, 2) a set of virtual orbitals of very high energy spinorbitals which are unoccupied in all determinants, 3) a set of active orbitals which are energetically intermediate between the inactive and virtual orbitals. In the conventional CI methods, the Hartree-Fock SCF wave function Ψ0 is used as a reference configuration and the configuration state functions are formed by moving electrons out of the occupied spinorbitals of Ψ0 into unoccupied spinorbitals. In multireference configuration interaction (MRCI) a set of reference configurations is created from which excited determinants are formed for use in a CI calculation. Large scale MRCI wavefunctions can generate very accurate wavefunctions but are also computationally very intensive.
In the present work, the theoretical ab initio investigation of the low-lying doublet and quartet electronic states of the BP+ ion-molecule and its potential energy calculations for the states 2s+1Λ(+/−) have been performed via the CASSCF method [13] [14] . A Multireference Doubly and Singly Configuration Interaction MRDSCI+Q with Davidson correction [15] -[17] was done via the computational chemistry Program MOLPRO [18] taking advantage of the graphical user interface GABEDIT [19] which runs with LINUX-type operating systems [20] . The boron and phosphorous species are treated in all electron schemes. The basis sets were chosen for s, p and d functions using aug-cc-pCVTZ;c and aug-cc-pVTZ;c for B and P atoms respectively from Molpro library. The CASSCF active space is 6σ (B: 2p, 3s; P: 3p0, 4s, 3d0, 4p0) and 4π (B: 2p±1; P: 3p±1, 3d±1, 4p±1) 1δ (P: 3d±2) orbitals in the C2v molecular orbitals are distributed into the irreducible representation a1, b1, b2 and 1a2 in the following way 6a1, 4b1, 4b2 , 1a2 noted [6, 4, 4, 1]. The 1s2 2s2 of B and 1s2 2s2 2p6 3s2 of P atoms were frozen in the MCSCF procedure. The number of active orbitals and valence electrons are 16 and 8 respectively.
3. Results and Discussion
The potential energy curves of the 26 doublet and quartet electronic states, in the representation 2s+1Λ± of the molecule BP+, has been performed for 189 internuclear distances. These curves are given in Figures 1-4.
One can notice some avoided crossings between different doublet and quartet electronic states. The repulsion between the two atoms, when they are brought close to each other, is related to the Pauli principle: when the electronic clouds surrounding the atoms start to overlap, the energy of the system increases abruptly. Moreover, some crossings, of abscissa Rc, and avoided crossings, of abscissa Rac, have been obtained between the potential energy curves of Figures 1-4. If the two curves correspond to states of different symmetry cross, they will ignore each other. Their wavefunctions Φ1 and Φ2 remain unperturbed and they are the adiabatic solutions of the Schrödinger equation. The crossing in this case is strictly allowed. But if these wavefunctions have the same symmetry, they will mix with each other to give two adiabatic solutions which no longer cross and the crossing
Figure 1. Potential energy curves of the doublet electronic 2Σ± and 2Δ states of the ion-molecule BP+.
Figure 2. Potential energy curves of the doublet electronic 2Π and 2Φ states of the ion-molecule BP+.
Figure 3. Potential energy curves of the quartet electronic 4Σ± and 4Δ states of the ion-molecule BP+.
Figure 4. Potential energy curves of the quartet electronic 4Π and 4Φ states of the ion-molecule BP+.
becomes avoided. The adiabatic solutions of the Schrödinger equation Ψ1 and Ψ2 are obtained by linear combinations of the diabatic ones where the variation method is used to solve for the coefficients. If H12 is the matrix element of the electronic hamiltonian H of the system between Φ1 and Φ2, the energy gap Eac between the two adiabatic states is twice the coupling term H12 at Rac. The calculated values of Rac and Eac are given in Table 1. Such crossings or avoided crossings can dramatically alter the stability of the molecule.
The spectroscopic constants such as the vibrational harmonic constant ωe, the internuclear distance at equilibrium Re, the rotational constant Be, and the electronic transition energy with respect to the ground state Te have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance by using the data obtained from the ab initio calculation. These values are given in Table 2 along with the rare available data in literature on this ion-molecule. The comparison of our calculated data with those in literature for the 4 electronic states X4Σ−, (1)2Σ−, (1)2Δ and (1)2Π one can find that an excellent agreement is obtained for the values of Re with the relative difference 0.5% < ΔRe/Re < 1.0% and a very good agreement for the values of Be with the relative difference 1.1% < ΔBe/Be < 4.9% with a larger relative difference for the state (1)2Π with the relative difference 8.2%. By comparing our calculated values of ωe with those in literature we found a very good agreement with relative difference 0.3%< ΔBe/Be < 4.0% for the 3 states X4Σ−, (1)2Σ−, (1)2Δ, while the agreement deteriorate for the state (1)2Π with the relative difference 23%. For our values of Te the relative difference is good for the (1)2Σ− with the relative difference 5.4% and becomes lager for the states (1)2Δ and (1)2Π with the relative differences 15% and 27% respectively. No comparison with other investigated states since, up to our knowledge, they are given here for the first time.
4. Permanent Dipole Moment
The permanent dipole moments are investigated for the considered electronic states of the ion-molecule BP+ by taking the boron atom at the origin, and the positions of the phosphorus atom are variable along the positive internuclear z-axis. All the calculations were performed with the MOLPRO [21] program. The dipole moment operator is among the most reliably predicted physical properties, because the quantum mechanical operator is a simple sum of one-electron operators. The expectation value of this operator is sensitive to the nature of the least energetic and most chemically relevant valence electrons. The positive sign of the dipole moment corresponds to a charge transfer from the P atom towards the B atom. To obtain the best accuracy, MRCI wavefunctions were constructed using MCSCF active space. The values of the permanent dipole moments, for the investigated electronic states, are given in atomic unites (a.u.) as a function of the internuclear distance R in Figures 5-8. One can notice that: 1) some of dipole moment curves, as (1)2Σ−, (2)2Σ+, (1)2Δ, (1,2,3)2Π, (1)4Σ−, (3)4Π, tend to ± ∞ when R tends the ∞ which explains the ionic bounding of all these in these regions, 2) some other dipole moment curves, as (2)4Σ−, (1,2,4)4Π, (1)4Δ, (1)4Σ+, (3)4Π, tend to constant limit where the bounding is covalent, 3) the agreement between the positions of the avoided crossings of the potential energy curves of 2 electronic states and the positions of the crossing of the dipole moment curves of these 2 states. This agreement may confirm the validity and the accuracy of the present calculation.
Table 1. Avoided crossings between the different electronic states of the ion-molecule BP+.
Table 2. Spectroscopic constants of the potential wells of the electronic states of the BP+ molecule.
aPresent Theoretical study using MRCI method; bRef. [1] ; cRef. [11] .
Figure 5. Dipole moment curves of the doublet electronic 2Σ± and 2Δ states of the ion-molecule BP+.
Figure 6. Dipole moment curves of the doublet electronic 2Π states of the ion-molecule BP+.
Figure 7. Dipole moment curves of the quartet electronic 4Σ± and 4Δ states of the ion- molecule BP+.
Figure 8. Dipole moment curves of the quartet electronic 4Π states of the ion-molecule BP+.
5. Conclusion
In the present work, ab initio calculation for 27 low-lying electronic states, in the representation 2s+1Λ(+/−), of the BP+ ion-molecule were computed via CASSCF/MRSDCI methods for the electronic excited states. The potential energy curves, the electronic energy with respect to the ground state Te, the harmonic frequency ωe, the internuclear distance Re have been calculated along with the rotational constant Be. The comparisons of the present results with the available values in the literature show an overall very good agreement. To the best of our knowledge, 23 new electronic states have been investigated for the first time through this work. These new excited electronic states may provide a reliable theoretical basis and information for the experimental spectral properties related to the electronic structure for BP+ ion-molecule and the relevant sub-system [22] [23] study as well.
Cite this paper
MahdiMansour,NaylaEl-Kork,MahmoudKorek, (2015) Ab-Initio Calculations of 27 Electronic States of the BP+ Ion-Molecule. Journal of Modern Physics,06,1781-1788. doi: 10.4236/jmp.2015.613180
References
- 1. Stewart, J.J. (1990) MOPAC: A Semiempirical Molecular Orbital Program. Journal of Computer-Aided Molecular Design, 4, 1-103.
http://dx.doi.org/10.1007/BF00128336 - 2. Zhu, Z.H. and Yu, H.G. (1997) Molecular Structure and Molecular Potentialenergy Function. Science Press, Beijing, 99, 102, 113.
- 3. Gingerich, K.A. and Piacente, V. (1971) Gaseous Phosphorus Compounds. IV. Thermodynamic Study of Gallium Monophosphide with a Mass Spectrometer and Dissociation Energy of Aluminum Diphosphide. The Journal of Chemical Physics, 54, 2498-2503.
http://dx.doi.org/10.1063/1.1675206 - 4. Boldyrev, A.I. and Simons, J. (1993) Ab Initio Study of Low-Lying Electronic States of XP (X = Li-B, Na-Si). The Journal of Physics Chemistry, 97, 6149-6154.
http://dx.doi.org/10.1021/j100125a011 - 5. Boldyrev, A.I., Gonzales, N. and Simons, J. (1994) Periodicity and Peculiarity in 120 First- and Second-Row Diatomic Molecules. Journal of Physics Chemistry, 98, 9931-9944.
http://dx.doi.org/10.1021/j100091a001 - 6. Gan, Z.T., Grant, D.J., Harrison, R.J. and Dixon, D.A. (2006) The Lowest Energy States of the Group-IIIA - Group- VA Heteronuclear Diatomics: BN, BP, AlN, and AlP from Full Configuration Interaction Calculations. The Journal of Chemical Physics, 125, Article ID: 124311.
http://dx.doi.org/10.1063/1.2335446 - 7. Chan, G.K.L. and Handy, N.C. (2000) An Extensive Study of Gradient Approximations to the Exchange-Correlation and Kinetic Energy Functionals. The Journal of Chemical Physics, 112, 5639-5653.
http://dx.doi.org/10.1063/1.481139 - 8. Bruna, P.J. and Grein, F. (2001) Electron-Spin Magnetic Moment (g Factor) of X2Σ+ Diatomic Radicals MX(±) with Nine Valence Electrons (M = Be, B, Mg, Al; X = N, O, F, P, S, Cl). An ab Initio Study. The Journal of Physical Chemistry A, 105, 3328-3339.
http://dx.doi.org/10.1021/jp003557+ - 9. Burrill, S. and Grein, F. (2005) Structure and Bonding of III/V Compounds X2Y2, with X = B, Al, Ga, and Y = N, P, As. Journal of Molecular Structure: THEOCHEM, 757, 137-142.
http://dx.doi.org/10.1016/j.theochem.2005.09.017 - 10. Qu, Y., Ma, W., Bian, X., Tang, H. and Tian, W. (2006) Electronic Structure and Stability of BP Clusters: Theoretical Calculations for (BP)n (n = 2 - 4). International Journal of Quantum Chemistry, 106, 960-967.
http://dx.doi.org/10.1002/qua.20818 - 11. Linguerri, R., Komiha, N., Oswald, R., Mitrushchenkov, A. and Rosmus, P. (2008) Electronic States of BP, BP+, BP-, B2P2. Chemical Physics, 346, 1-7.
http://dx.doi.org/10.1016/j.chemphys.2008.01.012 - 12. Guo, Y.-W., Zhang, X.-M., Liu, Y.-L. and Liu, Y.-F. (2013) Investigation on the Potential Energy Curves and Spectroscopic Properties of the Low-Lying Excited States of BP. Acta Physica Sinica, 62, Article ID: 193301.
- 13. Wang, W.B., Yu, K., Zhang, X.M. and Liu, Y.F. (2014) Ab Initio Calculation of the Potential Energy Curves and Spectroscopic Properties of BP Molecule. Acta Physica Sinica, 63, Article ID: 073302.
- 14. Shinsuke, H. (2008) Theoretical Study of Electronic Structure and Spectroscopy of Molecules Containing Metallic Atoms. PhD Thesis, Université Paris-Est, Paris.
https://tel.archives-ouvertes.fr/tel-00462184 - 15. Werner, H.J. and Knowles, P.J. (1988) An Efficient Internally Contracted Multiconfiguration-Reference Configuration Interaction Method. The Journal of Chemical Physics, 89, 5803-5814.
http://dx.doi.org/10.1063/1.455556 - 16. Langhoff, S.R. and Davidson, E.R. (1974) Configuration Interaction Calculations on the Nitrogen Molecule. International Journal of Quantum Chemistry, 8, 61-72.
http://dx.doi.org/10.1002/qua.560080106 - 17. Richartz, A., Buenker, R.J. and Peyerimhoff, S.D. (1978) Ab Initio MRD-CI Study of Ethane: The 14 - 25 eV PES Region and Rydberg States of Positive Ions. Chemical Physics, 28, 305-312.
http://dx.doi.org/10.1016/0301-0104(78)80007-X - 18. Werner, H.J., Knowles, G., Peter, J., Kinizia, G., Frederick, R. and Schütz, M. (2012) Molpro: A General-Purpose Quantum Chemistry Program Package. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2, 242-253.
http://dx.doi.org/10.1002/wcms.82 - 19. Allouche, A.R. (2011) Gabedit—A Graphical User Interface for Computational Chemistry Softwares. Journal of Computational Chemistry, 32, 174-182.
http://dx.doi.org/10.1002/jcc.21600 - 20. Knowles, P.J. and Werner, H.-J. (1988) An Efficient Method for the Evaluation of Coupling Coefficients in Configuration Interaction Calculations. Chemical Physics Letters, 145, 514-522.
http://dx.doi.org/10.1016/0009-2614(88)87412-8 - 21. Werner, H.J., Knowles, P.J., Lindh, R., Manby, F.R., Schütz, M., Celani, P., Korona, T., Rauhut, G., Amos, R.D., Bernhardsson, A., Berning, A., Cooper, D.L., Deegan, M.J.O., Dobbyn, A.J., Eckert, F., Hampel, C., Hetzer, G., Lloyd, A.W., McNicholas, S.J., Meyer, W., Mura, M.E., Nicklass, A., Palmieri, P., Pitzer, R., Schumann, U., Stoll, H., Stone, A.J., Tarroni, R. and Thorsteinsson, T. (2006) MOLPRO, a Package of ab-Initio Programs.
- 22. Wang, X.-Y. and Ding, S.-L. (2004) Constructing Potential Energy Surface of Tetratomic Molecules Using Lie Algebra. Acta Physica Sinica, 2, 17.
- 23. Han, H.-X., Peng, Q., Wen, Z.-Y. and Wang, Y.-B. (2005) Local Potential Energy Surface Analytical S2O and Vibrational Spectra of Molecules. Acta Physica Sinica, 54, 78-84.
http://www.cqvip.com/qk/94684x/200501/11794915.html
NOTES

*Corresponding author.










