Journal of Modern Physics
Vol.06 No.10(2015), Article ID:59224,4 pages
10.4236/jmp.2015.610145
Gravity, Not Mass Increases with Velocity
Eli Peter Manor
Israel Medical Association, Caesarea, Israel
Email: dr.eli.manor@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 June 2015; accepted 25 August 2015; published 28 August 2015
ABSTRACT
There are controversies and misunderstandings with the term “relativistic mass”. So, alternative concepts must be considered. It is postulated herewith that the stronger force required to accelerate an object moving at a faster speed is due to the increase of its inertia. That ensues in a rise in the gravitational force required to pull that object, and thereby brings to an increase in the gravitational constant. In this paper a formula is derived to calculate these variations in the gravitational constant, which is: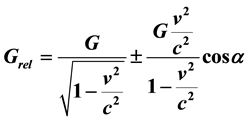 . This makes the use of the term “relativistic mass” unnecessary.
. This makes the use of the term “relativistic mass” unnecessary.
Keywords:
Relativistic Mass, Gravity Increase, Mass Definition, Inertia Related to Velocity, Gravity Due to Inertia

1. Introduction
Recently it has increasingly been recognised that the “relativistic mass” concept is troublesome [1] . The term “relativistic mass” is subject to misunderstandings as it makes the increase of the inertia of an object with velocity appear, as if it is connected to some change in the masses internal structure such as its cristallographic, chemical and nuclear properties. So, the concept of “relativistic mass” which increases with velocity is not compatible with the standard language of relativity theory [2] and it is unnecessary [3] and confusing [4] . It is important to realize that the property of mass of an object or particle does not increase with motion. The change is in energy [5] .
The more modern position is that there is only one mass, and it is speed-independent [6] . Many alternative conceptions formed in the last century to the original energy-mass relationship [7] .
The interpretation of special relativity that the mass of a relativistic body increases with velocity is an unfortunate consequence of relativity. In 1948 Einstein himself warned against the use of mass increasing with velocity [8] . So, using the word “mass” is quite confusing [9] . “Relativistic energy” is actually the proper replacement for “relativistic mass” [10] . It is more accurate to say that “inertia increases as velocity increases” [11] .
All the citations mentioned here indicate that an alternative notion to “relativistic mass” is desireable. Such a concept should replace the hypothesis that mass increases with velocity, however, should keep in line with relativistic physics.
2. Replacing Mass Increase with Gravity Increase
In Newtonian gravity theory, the gravitational acceleration in the spherically symmetric, static field of a point mass “M”, at distance “r” from the source, can be written [12] :

The gravitational constant is denoted by the letter “G”. The free-fall acceleration “a” is often marked as “g” which is the total gravitational field.
In this equation, it is common practice to describe an increase in velocity of an object ensuing in an increase of “M”. In order to avoid using the term “relativistic mass”, exactly the same graph format is attained by employing an increase of “G” with increasing speed of an object.
Mass may be defined as matter that measures its resistance to acceleration. This includes resistance to a gravitational force. According to the special theory of relativity mass increases with speed according to the formula:

However, that can be substituted by gravitational increase and not mass increase:
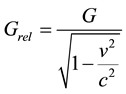
This exchange of “M” by “G” is obvious, as by increasing the velocity of an object its inertia increases, requiring change in gravitation, and not requiring mass increase.
Gravity is directional, and whichever formula is employed, both if “M” or if “G” increases, the direction of the force must be taken into account.
The discrepancy between receding and approaching objects is obvious, as it is harder to accelerate an object against its direction of movement than if it moves in the same direction. So in equations for objects attracted by the gravitational force of earth and moving vertically, the direction is important.
For receding objects moving vertically to earth, the formula is:
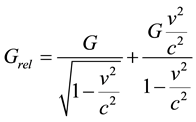
For objects approaching toward earth the formula is:
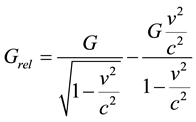
The same applies to any two objects, not just related to earth.
For objects moving perpendicular to the direction of the gravitational force, no change of the initial formula is required.
For objects moving in directions in between vertical and horizontal directions to the gravitational pull, trigonometric functions must be added. This can be done by multiplying the right-hand part of these formulae with cosα. α is the angle between the vectors of the direction of movement and the direction of the pulling force. So the equations become:
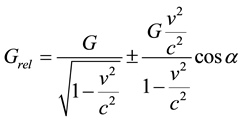
(see Figure 1).
3. Further Explanations of These Formulae
If, by definition, an object is moving at an invariant speed, although it is exposed to a gravitational force, pulling it, the change which occurs for objects moving at different speeds must be that of the gravitational force. That change is related to the speed of the object.
An object at rest, the gravitational force required to accelerate it toward earth is “g” (9.8 m/s²).
For a receding object, its direction is opposite to the gravitational pull. Therefore, the faster it moves, the harder it becomes to pull it toward earth. So the gravitational force required must be stronger. This, until an object recedes at a speed close to the velocity of light © where the force required is almost infinite.
For an object approaching earth, its inertial force is in the same direction as the gravitational attraction. So the force required to accelerate it towards earth is less than that pull required for an object at rest. The faster an object approaches earth, the less gravitational force is required to attract it. However, for objects at a certain velocity, the objects inertial force equals the force required to pull it. That velocity can be calculated, and is v = 0.78615 c. Up to this speed, the faster an object approaches earth, the less pulling force is required to pull it in order to accelerate its approach.
Objects approaching still faster, their inertia is stronger than the exerted gravitational force required to accelerate it. So to say, it “overtakes” gravitation. So the force causing their acceleration will bear a negative (−) sign. From that velocity onwards, objects approaching earth at faster speeds have a larger inertial force, although it is bearing a negative sign. Objects with speeds approaching that of light will have an almost indefinite inertia.
Inertia of an object is its resistance to any change in its state of motion, including speed and direction. For that reason, if the inertial force bearing a (−) sign, its force is just like that bearing a (+) sign.
Figure 1. Graphical representation.
This is similar to the so called “mass increase”, which is assumed to increase, independent to the direction of movement. This, although for an approaching object there is an apparent “mass decrease” [13] . The magnitude of the force depends on the objects velocity, and not on its direction.
One of the pillars of Einstein’s Relativity is the principle of equivalence: the equivalence of inertial mass and gravitational mass. Here, it comes to be the equivalence of inertial force and gravitational force.
4. Implications of Gravitational Force Increase
With increase of a body’s gravity, due to increase in the gravitational constant, there is an increase in a contracting force, therefore, theoretically, a possible increase in density. The increase of density of a body causes its length shortening. That is the well known relativistic length shortening. The gravitational increase with velocity of moving objects, ensuing in increased density, might effect radioactive decay. In denser objects radioactive decay may slow down. Time dilation is usually considered to be related to velocity. As shown here, velocity effects gravity, so also time dilation is related to gravity.
The formula of time dilation is:

It is just the same if mass or gravity increases. Therefore time dilation is also consistant with the assumption that “G”, not “M”, increases with velocity.
5. Conclusions
The inertia of a moving object is dependent on its mass and speed of motion. With increase of that energy it becomes harder to change the objects motion―acceleration, deceleration and deviation from its course. Accord- ing to the main stream relativistic theory, this is due to the increase of the relativistic mass of the object. That requires more than one interpretation of what mass means. One is that mass does not change and is called “invariant mass” or “rest mass”. The other “relativistic mass” is energy dependent, increasing with velocity. That requires changes in its properties. For that reason, alternative interpretation for the increase of resistance depending on the velocity of the object must be sought.
In this paper, the increase of the inertia of an object with increase in its speed is related to changes of the gravitational force, and so in the gravitaional constant. This solves the disparity of defining “mass”.
To overcome the inertial force of a given mass, the gravitational pull must be at least of the same magnitude. If that mass moves at an invariant speed, and its mass is constant, the gravitational attraction exerted by earth must be related to the velocity of that mass. Einstein reinforced the relationship between gravity and inertia by declaring their equivalence. Both exert the same force on an invariant mass with an invariant speed. It turns out that the gravitational constant “G” is dependent on the pace of the mass. As inertia and gravity have a vector, formulae are developed to cope with this issue.
An object’s inertia changes its gravitational behavior, so it seems “as if” its mass changes. The variations of the inertia of a body only make it seem “as if” it is the mass that varies. So the concept presented here solves the problem with the term “relativistic mass”.
Although it is the inertia, not the mass that increases with speed, it seems erroneous “as if” the mass is gaining more mass. Therefore, it is suggested to call it “as if” mass. This change to the generally accepted terminology is not too dramatic.
Cite this paper
Eli PeterManor, (2015) Gravity, Not Mass Increases with Velocity. Journal of Modern Physics,06,1407-1411. doi: 10.4236/jmp.2015.610145
References
- 1. Okun, L.B. (1989) Physics Today, 42, 31-36.
http://dx.doi.org/10.1063/1.881171 - 2. Okun, L.B. (2009) American Journal of Physics, 77, 430-431.
http://aapt.org/ajp
http://dx.doi.org/10.1119/1.3056168 - 3. Prasad, J. (2010) Einstein’s E = mc2.
http://www.iucaa.ernet.in/~jayanti/docs/e_is_equal_mc2.pdf - 4. Gibbs, P. (1997) Addendum Added by Don Koks 2002, Does Mass Change with Velocity?
http://sasuke.econ.hc.keio.ac.jp/~ken/physics-faq/mass.html - 5. Ranzan, C. (2013) Applied Physics Research, 5, 84-90. ISSN 1916-9639, E-ISSN 1916-9647.
- 6. Hecht, E. (2009) The Physics Teacher, 47, 336-341.
http://scitation.aip.org/content/aapt/journal/tpt/47/6/10.1119/1.3204111 - 7. Leong, W.C. and Chin, Y.K. (2005) New Horizons in Education, 51, 56-66.
- 8. Zapper, Z. (2009) Physics Blog on the World of Physics and Physicists, Rest Mass versus Relativistic Mass.
http://physicsandphysicists.blogspot.co.il/2009/04/rest-mass-versus-relativistic-mass.html - 9. Strassler, M. (2013) The Two Definitions of “Mass” and Why I Use Only One.
http://profmattstrassler.com/articles-and-posts/particle-physics-basics/mass-energy-matter-etc/more-on-mass/the-two-definitions-of-mass-and-why-i-use-only-one/ - 10. Todd, J. (2012) The General Science Journal.
http://gsjournal.net/Science-Journals/Research%20Papers-Relativity%20Theory/Download/3960 - 11. Lincoln, D. (2014) Physics in a Nutshell.
http://www.fnal.gov/pub/today/archive/archive_2014/today14-04-04_NutshellReadMore.html - 12. Tensor-Vector-Scalar Gravity.
http://self.gutenberg.org/articles/tensor-vector-scalar_gravity - 13. Mathis, M. (2004) How New Transforms in the Special Relativity Affect Mass, Momentum and Energy Equations.


