Journal of Modern Physics
Vol.06 No.08(2015), Article ID:57909,6 pages
10.4236/jmp.2015.68108
Linac Beam Dynamics Code Benchmarking
Xuejun Yin1,2, Wolfgang Bayer2, Andrea Franchi3
1Institute of Modern Physics of Chinese Academy of Sciences, Lanzhou, China
2GSI Darmstadt, Planckstrasse 1, Darmstadt, Germany
3ESRF, CS 40220, 38043 Grenoble Cedex 9, France
Email: yinxj@impcas.ac.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
The code benchmarking for hadron linac using the 3D Particle-In-Cell (PIC) code is an important task in the European framework “High Intensity Pulsed Proton Injector” (HIPPI). PARMILA and HALODYN are two of the codes involved in this work. Both of these codes have been developed and used for linac design and beam dynamics studies. In this paper, the simulation results of the beam dynamics were compared and analyzed. As predicted by two codes, the simulation results show some agreements. The physical design strategy which was adopted in two codes was also discussed.
Keywords:
Hadron Linac, 3D PIC Code Benchmark, Beam Dynamics Simulation

1. Introduction
One main task of the HIPPI beam dynamics work group is to compare the validation of the 3D linac codes in the high current regime. It demands to find how much agreement the tracking simulations have with each other and to analyze the code validation based on these results. Some codes are available and currently run for such simulations. Some comparison works have been performed [1] . In the overview paper [2] , it describes the comparison step and tracking simulation based on the lattice of UNILAC Alvarez DTL at GSI.
As one knows, various approaches were used to describe the space charge effects and different lattice modeling may pose severe problems to understand the source of discrepancies when the tracking simulations are run at high current status. For this reason the code benchmarking has been divided in three steps. The first two steps are the static comparison of space charge calculation and tracking simulation with a zero-current beam current. In the second step, a common Gaussian distribution as the initial conditions was input for comparison among codes.
The third step is the tracking simulation with high current. It also uses a common Gaussian distribution. However in this step, two cases are considered [3] . In the case1, the bunch beam is spherical 6D Gaussian distribution (truncated at 3σ) in three dimensions. It means that the transverse and longitudinal planes have the same RMS values. The case2 is an ellipsoidal 6D Gaussian distribution (also truncated at 3σ), but the longitudinal emittance is one order of magnitude larger than that of transverse ones. In this paper, we mainly study focusing on the second case.
In this study, the 3D PIC tracking simulations have been performed with HALODYN and PARMILA. As the predictions of two codes, these simulation results show some agreement compared with each other. The reasons of emittance growth are also explained in details. And the different physical models of two linac codes are discussed based on these simulation results.
2. Codes
The code PARMILA (Version 2.35) [4] was originally written only for DTLs. Over the last several years, it has been extensively modified to include coupled cavity and superconducting structures [5] . Over the same period, several other linac codes have been developed independently. The Department of Physics at the University of Bologna has written a code HALODYN [6] . The main feature of this code is the space-charge field can be computed on a 3D spatial grid and interpolated to be obtained at each point occupied by the particles.
PARMILA is a scalar code developed in Los Alamos (LANL) [7] . The user can choose either a 2D r-z (SCHEFF) or a 3D (PICNIC) PIC Poisson solver with open boundary conditions. The DTL structure has been defined by using the “DTL” command line. With this option, once the entrance energy and the number of cells are defined, the code builds automatically the DTL tank. In the DTL, PARMILA gives the space-charge kick at the center of each cell. The RF is modelled making use of either the Transit-Time-Factor (TTF) table generated by SUPERFISH or a nonlinear thin kick. PARMILA uses the gap impulses applied at the electrical center of the DTL cell; off axis fields are derived using Bessel function expansions. It uses the expansion of the longitudinal electric field in terms of the transit-time factor integrals computed by the SUPERFISH postprocessor SFO. In the calculation of space-charge effect, PARMILA also applies the PIC method. This code computes the space- charge forces by assuming an elliptical cylindrical symmetry of the beam bunch. The bunch is approximated by a number of concentric and parallel triodes, each carrying a uniformly distributed charge. Each particle behaves as a ring of charge that contributes to the electric field on a two-dimensional (r, z) mesh. Thus the space is mapped with a 2D mesh in the beam. The number of intervals in each dimension of the space-charge mesh is fixed at a user-defined setting for an entire beam-dynamics run. In our calculation, the initial mesh intervals in the radial DRSC and longitudinal directions DZSC are both 0.05 cm, and the number of mesh intervals in these directions NR, NZ are 20 and 40 respectively. Thus the maximum extent of the space charge mesh is (initially) NRDRSC in the radial direction and NZDZSC in the longitudinal direction. The numbers of beam bunch both ahead and behind of the interest bunch is one.
HALODYN is also a Particle-In-Cell code. In the DTL sections, the transport elements are described by a sequence of drift, quadrupole and thin-lens RF cavities, whose accelerating voltage is calculated from the mean value of the accelerating electric fields. The RF cavities are modelled by using the thin lens approximation and the off-axis fields are derived with the modified Bessel functions. The space charge field is computed based on a 3D PIC spectral Poisson solver with closed boundary conditions defined on a rectangular pipe [8] . In the particles tracking simulation, HALODYN adopts a micromap approach that take into account the space charge effects at each time step by using the Vlasov model. It treats the space-charge force as an impulsive force and tracks particles through a linac by using z as independent variable and the Cartesian coordinate (x, y, z) relative to the synchronous particle. The Poisson solver is based on a 3D FFT. In our calculation, the grid resolution of HALODYN codes is 32 × 2048.
Additional HALODYN code has been developed under the UNIX environments system, but PARMILA runs in the Windows platform. More details of the individual codes can be found in the references cited above. Both of these codes treat the space-charge distribution as a round ellipsoid. Both codes use z as the independent variable to transport the beam particles through the linac described as a sequence of elements. All the codes use hard-edged quads. None of the codes included fringe-field effects.
3. Tracking Simulation
As part of our effort to compare the beam simulation results from two different codes, we choose to start with the UNILAC Alvarez DTL tanks (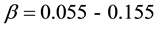 ). The beam from the RFQ-IH Linac and a gas stripper section was transported to Alvarez DTL post stripper at the energy of 1.4 MeV/u and 108.408 MHz. The five DTL tanks have 178 cells delivering beam at 11.4 MeV/u.
). The beam from the RFQ-IH Linac and a gas stripper section was transported to Alvarez DTL post stripper at the energy of 1.4 MeV/u and 108.408 MHz. The five DTL tanks have 178 cells delivering beam at 11.4 MeV/u.
Based on the previous simulations, the initial particle distribution was spherical and the energy spread was one order of magnitude lower than the measured one. The following simulations track a particle distribution with longitudinal emittance one order of magnitude larger than the transverse ones, resulting in a much lower longitudinal tune depression (case2). The latter choice is motivated by the fact that the space-charge routine SCHEFF implemented in PARMILA is a 2D r-z solver, and its interest is to test how robust is this approximation for an asymmetric bunched beam. The input distribution is as usual a 6D-Gaussian (truncated in each phase space at 3σ), representing a 238U+28 beam of 37 mA with kinetic energy W = 1.4 MeV/u. Other Twiss parameters and lattice parameters are listed in Table 1. Using the obtained distribution as an input for HALODYN and PARMILA, the simulations should be compatible.
The phase advances are computed over the first focusing period. The depressed phase advance is computed assuming a 6D uniform space-charge distribution. No coupling exists between the planes.
Figure 1 shows the evolution of the transverse RMS emittance as a function of distance along the DTL Tanks. Basically both codes get agreement in terms of the transverse RMS emittances. In the horizontal plane (left plot) the codes begin to diverge already inside the first tank (≈10 m). The emittance growth ratios are 1.24 and 1.33 in horizontal, 1.26 and 1.25 in vertical for HALODYN and PARMILA simulations at the first tank exit, respectively. The final horizontal emittance presents a large spread of about ±4.7%, whereas in the vertical plane the discrepancies remains confined to ±1%. This demonstrates that codes with the 2D Poisson solver SCHEFF are well within these values, confirming the robustness of the r-z approximations for the beam parameters under consideration.
Table 1. Initial RMS beam parameters and lattice parameters of simulations.
Figure 1. Horizontal (left) and vertical (right) normalized transverse RMS emittance profiles computed by two codes through the UNILAC DTL Tanks.
By further studying we can find that the main contribution of the emittance growth comes from the first DTL tank. For example, the emittance growths ratios at the first tank exit are 1.24 and 1.33 for HALODYN and PARMILA code simulation in the horizontal plane, respectively. They are the 39.2% and 41.7% of the total growth ratio. It may be explained by the focusing structure of the DTL. The focusing lattice is designed as the DFFD in the first DTL. The emittance growth occurs at the period structure in which the focusing strength is not smooth. For instance in the seventh period, the focusing strengths of the first two quadrupole were 1709.4 G/cm, but the rest two in the same period were 1681.3 G/cm. Thus the evolutions of the phase advance along the DTL tanks are not enough smooth.
To further compare the calculate results of space-charge effects between two codes, we also plot the distribution in phase space as shown in Figure 2.
Table 2 presents the final RMS values calculated by two codes. As can be found in Table 2, the simulations results of both codes are basically agreement with each other both in vertical and longitudinal planes. Furthermore, we can observe that a little discrepancy occurs in horizontal plane between two codes. A more reasonable conclusion is that there is some idealized assumption common to the two codes, which leads to disagreement with data. One of the reasons may be the coupling between x-y or x-z in the initial particle distribution with space charge effect. Another guess would be inaccurate treatment of the rf cavity fields. It depends on the numerical algorithms which were applied in both codes.
For a quantitative comparison, we also show the output radial distribution of the particles in Figure 3. We can find that there are almost no difference up to ~0.65 cm, which essentially represents the main core of the beam, both codes predicts virtually identical distributions. The largest divergence occurs around the edges (r > 0.8 cm)
Figure 2. Horizontal (x-x′) and vertical (y-y′) phase space plots at the entrance and exit of the UNILAC DTL Tanks.
Table 2. The final RMS distribution parameters obtained by two codes.
Figure 3. Particle radial distribution at the exit of the DTL Tanks.
i.e. halo region of the bunch. The difference around the extreme outer edges of the beam is at the level of <0.04 mA.
More peculiar behaviour is the evolution of the longitudinal emittance as shown in Figure 4 (down curve). In the longitudinal plane, there are no obvious discrepancies in both codes before tank 4. But from the entrance of tank4, the discrepancies become clearly. And the longitudinal emittance blow up in tank 4 predicted by both codes starting. A large dilution of the longitudinal phase space is accompanied to the emittance increase. It is believed that the peculiar and code-dependent behaviour after the first half of tank 4 is mainly driven by few particles close to the edge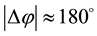 .
.
By comparing the evolution of the longitudinal phase space predicted by both codes, it was possible to conclude that they describe the same longitudinal beam dynamics. It was thought that the reason of the large discrepancies in the emittance curves, as well as of the different predictions in term of beam loss, might be in the different definition of particle loss in the longitudinal plane. After the code adjustments carried out as in the previous case, it has been observed that results are highly sensitive to the definition of particle loss in the longitudinal plane. Few particles far from the RF bucket area, if included in the computation of the RMS quantities, might drive to an unrealistic overestimation. While this definition in the transverse coordinates is rather straight- forward.
There are some reasons to explain it. One reason is the longitudinal mismatch from the entrance of UNILAC. This initial mismatch drives a beam dilution through the space-charge. Another is the fact that the synchronous phase jumps from −30˚ to −25˚ when particles transport from tank3 to tank4. The bucket area shrinks at the same time. The longitudinal emittance experiences a weak growth due to the large bucket area in the first three thanks. When entering in tank 4, the phase jump accompanying the bucket area shrinks makes the bunch tails cross the separatrix, leading eventually to a even larger phase space dilution.
In Figure 4 it also shows how much degree the longitudinal RMS emittances can be depending on the particle loss definition (up curve). HALODYN will cut-off particle whose phase comparing to the synchronous phase is 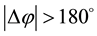 in longitudinal plane. But PARMILA cut-off particle whose energy spread relative to the reference energy is larger than 3% at each end of tank [3] . As we can observe form Figure 4, in the middle of tank4, for HALODYN, the particle loss is much higher than that of PARMILA, corresponding the emittance of HALO- DYN is smaller than that of PARMILA. In the final, the beam losses are 2.2% and 1.9% for HALODYN and PARMILA respectively.
in longitudinal plane. But PARMILA cut-off particle whose energy spread relative to the reference energy is larger than 3% at each end of tank [3] . As we can observe form Figure 4, in the middle of tank4, for HALODYN, the particle loss is much higher than that of PARMILA, corresponding the emittance of HALO- DYN is smaller than that of PARMILA. In the final, the beam losses are 2.2% and 1.9% for HALODYN and PARMILA respectively.
The calculated RMS emittance and growth ratios were summarized in Table 3. Basically the simulation results of both codes get excellent agreement not only in terms of the transverse RMS emittances but also in that of longitudinal plane. This demonstrates that codes with the 3D FFT in HALODYN and 2D Poisson solver SCHEFF in PARMILA are well within these values, confirming the robustness of the r-z approximations for the beam parameters under consideration. Both of the horizontal emittance values are larger than those of vertical planes at the DTL exit, which should be carefully checked with the experiment results in the future.
4. Conclusions
These study results presented here show remarkable agreement between the predictions from 3D PIC code HALODYN and PARMILA. Generally the simulation results performed by two codes get agreement both in the transverse and longitudinal plane. The reason of the emittance growth was also analyzed in details.
These results demonstrate that the codes with the 3D FFT in HALODYN and 2D Poisson solver SCHEFF in PARMILA have the robustness of the r-z approximations for the beam parameters under consideration. It leads to conclusion that no gross errors have been made in the physics or methods of the codes. Of course, these studies should be investigated further with other codes.
Figure 4. Normalized longitudinal RMS emittance and particle trans- mission along the DTL.
Table 3. The simulated emittance and growth ratios.
Acknowledgements
The author thanks Dr. Prof. Ingo Hofmann for helpful discussion. We are also grateful to Dr. Andreas. Sauer (IAP. Frankfurt University) for his continue support on PARMILA.
We also acknowledge the support of the European Community-Research Infrastructure Activity under the “FP6” Structuring the European Research Area program.
Cite this paper
XuejunYin,WolfgangBayer,AndreaFranchi, (2015) Linac Beam Dynamics Code Benchmarking. Journal of Modern Physics,06,1044-1050. doi: 10.4236/jmp.2015.68108
References
- 1. Nath, S., Qiang, J., Ryne, R., et al. (2002) Comparison of Linac Simulation Codes. Proceedings of the Particle Accelerator Conference, Chicago, 18-22 June 2001, 264-266.
- 2. Franchi, A., Duperrier, R., Franchetti, G., et al. (2005) Benchmarking Linac Codes for the HIPPI Project. AIP Conference Proceedings, Bensheim, 18-22 October 2004.
- 3. Yin, X., Bayer, W., Franchi, A., Hofmann, I., et al. (2006) Status of Code Benchmarking for HIPPI. HIPPI Annual Meeting, FZJ, 27-29 September 2006.
- 4. Swenson, D.A. and Stovall, J.E. (1968) PARMILA. Los Alamos national Laboratory internal Memorandum, MP-3-19, January 1968, 12.
- 5. Takeda, H., Young, L.M., Nath, S., Billen, J.H. and Stovall, J.E. (1996) Linac Design Algorithm with Symmetric Segments. Proceedings of the XVII International Linac Conference, Geneva, 26-30 August 1996, 3 p.
- 6. Franchi, A., et al. (2002) A 3D Poisson-Vlasov Code to Simulate the Space-Charge Effects in the High Intensity TRASCO Linac. Proceedings of the XXI Linac Conference, Gyeongju, 19-23 August 2002, 653-655.
- 7. Billen, J.H. (2004) PARMILA. LA-UR-98-4478.
- 8. Turchetti, G., Turchetti, G., Benedetti, C., Mattioli, F. and Franchi, A. (2006) Nuclear Instruments and Methods in Physics Research Section A, 561, 223-229.






