Received 7 April 2015; accepted 27 September 2015; published 30 September 2015

ABSTRACT

We study the quantum theory of the mass-less vector fields on the Rindler space. We evaluate the Bogoliubov coefficients by means of a new technique based upon the use of light-front coordinates and Mellin transform. We briefly comment about the ensuing Unruh effect and its consequences.

Keywords:

Rindler Space, Unruh Effect, Vector Fields, Bogoliubov Coefficients

1. Introduction

The production, propagation and detection of real photons in a non-inertial reference frame are a highly nontrivial subject [1] [2] . The matter is that, if one aims to describe those features in a coordinate independent way, i.e. local diffeomorphism invariant in the physical 3 + 1 dimensional space-time, one has to properly separate the physical and nonphysical polarization modes, the latter ones being necessarily present in any gauge and diffeomorphism invariant general formulation of the quantum theory: this becomes a hard task which has not yet been reached, even for a uniformly accelerated frame in a flat space-time referred to a curved coordinate system [3] . Actually, in the nearly whole literature on the non-inertial effects on quantum fields, just like the celebrated Unruh effect [4] , or about quantum field theory in curved spaces, the emphasis, examples and applications are always centered around the real scalar field case [4] - [9] up to some few exceptions concerning the realistic electromagnetic or Proca vector fields [10] - [12] or the Dirac and Majorana spinor fields [13] [14] . Recently, a quite interesting attempt to investigate, both from a theoretical and operational points of view, the process of emission, propagation and detection of electromagnetic radiation in a uniformly accelerated reference frame has been pursued in [2] in the four dimensional space-time. However, to the aim of avoiding the difficult disentanglement of the physical and nonphysical polarization, the author does restrict the dynamics along the acceleration direction, just turning to a 2-dimensional setting and to the treatment of the radiation field in terms of a conventional mass-less scalar degree of freedom in a 1 + 1 dimensional Minkowskian space. But in so doing, it turns out that the correct canonical quantization [15] of the radiation field is not properly taken into account so that, consequently, some fictitious singularities appear, which are an artifact of the too drastic simplification of the radiation dynamics in an accelerated reference frame hitherto employed.

It is the aim of the present short note to fill this lack and to provide a fully consistent Lorentz and gauge invariant quantum theory for the lineal, i.e. on a one dimensional spatial real line, radiation field. In so doing, thanks to a new method based upon the use of the Mellin transforms and the light-front system of coordinates, which has been recently developed by Aref’eva and Volovich [16] , the Bogoliubov coefficients connecting inertial and accelerated reference frames are eventually and correctly obtained to be singularity free. Thanks to the present contribution, the quite relevant and interesting operational analysis developed in [2] is actually set on a firm and reliable framework and might become seminal for some future experimental verification.

2. Rindler Space and Coordinate System

¹Throughout this note we shall use natural units 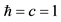unless explicitly stated.

In this Section we aim to briefly collect and recall the most useful systems of coordinates, which are utmost suitable to describe the field dynamics for a uniformly accelerated Observer in the Rindler space [17] , a non- inertial flat space-time in two dimensional curved coordinate systems―many more details and useful properties, aspects and relevant features can be found in [18] . To this concern, consider a two dimensional Minkowskian space with coordinates1

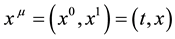
and metric

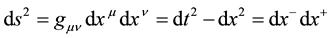(1)

where is the metric tensor while

are the standard light-front coordinates. If we perform the non-inertial coordinate transformation in the restricted space-like region 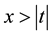of the Minkowskian space

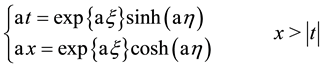(2)

with 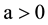and or equivalently

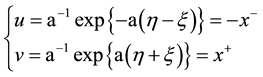(3)

then the line element of Equation (1) becomes

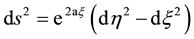(4)

Moreover we can readily obtain the inversion formulæ for

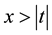
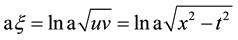(5)

(6)

whence we get

(7)

(8)

in such a manner that if we set then we find

(9)

(10)

Finally we can readily find the transformation formulæfor the differential operators, viz.

(11)

(12)

(13)

The curved coordinates cover only a quadrant of the Minkowskian space i.e. the Rindler region R named the right Rindler wedge [17]

Since lines of constant η are straight while lines of constant ξ are just hyperbolas

(14)

the asymptotic of which are the null rays or Thus the accelerated Observers do indefinitely approach the speed of light for while the proper time and the proper acceleration for the accelerated Observers are respectively given by

(15)

in such a manner that hyperbolæ of large negative ξ, i.e. close to the Rindler horizon do represent strongly accelerated Observers with a short proper time.

As a further quite useful example of curved coordinate system to label the two dimensional Rindler space, consider once again the sub-spaces R and L of the Minkowskian space in the curved coordinate system associated to the uniformly accelerated Observer: namely,

(16)

where the plus and minus signs refer to the right and left Rindler’s wedges respectively, while the line element takes the forms

(17)

whence we obtain the metric tensors

(18)

so that

(19)

Moreover, after setting

we readily get the transformation matrix

(20)

where Notice that, in general, the transformation matrix connecting the inertial and the accelerated reference frames can be written as the product of a local Lorentz transformation and the Zwei-Beine field

(21)

and specifically, for the present case of a uniformly accelerated Observer,

(22)

(23)

(24)

Hence we can eventually write the following chain equality

For any contravariant vector field in the Minkowski space we can derive the corresponding vector field in the Rindler space, viz.,

(25)

Consider for example the complete orthogonal set of the mass-less vector normal modes in the 2-dimensional Minkowski space

(26)

where the dual pair of constant light-like polarization vectors is provided by

(27)

while the scalar wave functions read

(28)

The Minkowskian space vector normal modes do fulfill

(29)

where the invariant inner product is defined by

(30)

The complete and orthogonal set of the mass-less vector normal modes in the right Rindler wedge R can be readily obtained from Equations (21) and (25). To this concern it is expedient to introduce the accelerated polarization vectors

(31)

in such a manner that we eventually come to

(32)

where

(33)

with and.

3. Quantization of the Lineal Radiation Field

The manifestly covariant quantization of the free radiation field on a two dimensional Minkowskian space in the non-homogeneous Lorenz gauge can be suitably performed according to the well known and long standing procedure and formalism developed by Bleuler, Gupta, Lautrup and Nakanishi [15] in the four dimensional case. The Lagrangian is

(34)

where is the auxiliary scalar field, while is the gauge parameter, so that the field equations read

(35)

It turns out that the following general canonical commutation relations hold true: namely,

(36)

(37)

(38)

(39)

where the mass-less Pauli-Jordan real and odd distribution is provided by

(40)

(41)

(42)

(43)

whereas is named the mass-less dipole-ghost invariant distribution, which is defined by the property

an integral-differential representation being given by

(44)

An explicit expression can be obtained as follows. Let us first consider the positive and negative Wightman functions, i.e. the positive and negative parts of the Pauli-Jordan distribution, in the two dimensional Minkowskian space

whence it is clear that the positive and negative parts of the Pauli-Jordan commutator are complex conjugate quantities

Consider now the integral for

(45)

and change the variable so that Then we obtain

Here so that two cases should be distinguished, i.e. and. After setting it is convenient to carry out respectively the substitutions

in such a way that we can write

Now we can use the integral representations of the Bessel functions of real and imaginary arguments [19] that eventually yield for arbitrary and

and thereby

(46)

(47)

(48)

so that

(49)

while the mass-less dipole-ghost in two space-time dimensions becomes

(50)

It is a simple and instructive exercise to verify the compatibility between the above general covariant canonical commutation relations and the equations of motion, for,

together with

(51)

Moreover one can readily check that the initial conditions fulfilled by the above general covariant canonical commutation relations are

all the remaining equal-time commutation relations being equal to zero. The most general solution of the canonical commutation relations in the non-homogeneous Lorenz gauge can be written in the form

(52)

(53)

where are the destruction operators which satisfy the canonical commutation relations

(54)

all the other commutators vanishing. The canonical commutation relations indicates that the Fock space is of indefinite metric, so that a physical Hilbert sub-space with semi-definite metric is selected by the subsidiary condition

(55)

where

is the positive frequency part of the auxiliary scalar field operator. It follows therefrom that, for instance, the 1-particle states describe Lorenz lineal nonphysical photons, while the 1-particle states do represent the physical lineal scalar photons, which are all of zero norm and satisfy (55) just owing to the canonical commutation relations (54).

Things greatly and neatly simplify in the Feynman gauge that we shall select in what follows without loss of generality. Notice that if we set

(56)

we can recast the covariant wave equations and the non-homogeneous Lorenz condition in the light-front form

(57)

(58)

(59)

It turns out that the mass-less vector wave equations and gauge condition in a two dimensional Minkowskian space possess the set of light-like solutions

(60)

(61)

where while

(62)

does represent the standard orthogonal set of mass-less scalar modes. As we have

(63)

it follows that the Lorenz condition is satisfied only for the longitudinal normal modes, viz.,

(64)

Notice that the polarization vector is indeed a Minkowski bi-vector, because it can be written in the form

(65)

the other light-like bi-vector being the dual of the bi-vector labeling the energy-momentum carried by the normal mode

In order to set up a complete orthogonal basis of mass-less vector modes on the Minkowskian space,

one has to introduce the dual light-like polarization vector such that

(66)

It turns out that all the normal modes (61) are of positive frequencies with respect to the time-like Killing vector, for they fulfill

(67)

It is also useful to introduce the light-front components of the light-like polarization vectors that read

(68)

The normal modes with consist of the trigonometric functions of the light-front spatial variables see equation (3)

It turns out that in the standard instant-form coordinates those normal modes do represent wave fronts propagating from left to right along the Ox-line with unit velocity, so that we can conclude that the trigonometric functions of the variable do describe progressive waves.

Conversely, for one has to deal with the trigonometric functions of the other light-front temporal variables so that

which shows that the trigonometric functions of the temporal light-front variable actually correspond, in instant-form coordinates, to regressive waves moving with unit velocity from right to left along the Ox-straight line.

It is worthwhile to remark that the mass-less normal modes for the auxiliary scalar field are normalized according to the Lorentz invariant inner product

(69)

while the polarized vector normal modes in the Feynman gauge are normalized according to the Lorentz invariant inner product

(70)

which fulfill

(71)

The vector normal modes do represent the wave functions of the lineal photons with definite momentum and polarization satisfying the Lorenz condition because while describe the scalar lineal photons because

(72)

Putting altogether we can write the light-front components of the Feynman gauge vector potential in the form

(73)

(74)

(75)

together with

(76)

(77)

(78)

Moreover, from Equation (53) we get the normal mode expansion of the auxiliary scalar field

(79)

It is worthwhile to remark that the above expressions manifestly satisfy both the D’Alembert wave equation as well as the non-homogeneous Lorenz condition because

(80)

(81)

while the electric field strength is provided by

(82)

4. The Bogoliubov Coefficients

It is very convenient to write

(83)

(84)

in such a manner that one gets a representation for the solutions of the wave equations and the Feynman gauge subsidiary condition in the Rindler’s regions R and L, the two regions being interchanged by parity and time reversal symmetry. Actually, in the Rindler’s regions L and R one may adopt an alternative expansion based upon the Rindler’s counterparts of the massless scalar normal modes on the Minkowskian space. To this concern, we remark that the metric (4) is conformal to the whole Minkowskian space, so that under the conformal transformation, the line element reduces to. Since the D’Alembert wave equation as well as the Lorenz condition are conformally invariant, we can recast the latter in Rindler’s coordinates as

(85)

(86)

for which there exist normal mode solutions

(87)

It follows that from Equation (3) we eventually find for, i.e. in the right Rindler wedge,

(88)

(89)

where do represent the holomorphic amplitudes of the Lorenz gauge potential on the the right Rindler wedge.

The relation between the normal modes expansions of the quantum fields in the Minkowski and Rindler spaces is well known [1] [4] [5] and expressed by the Bogoliubov coefficients, which satisfy a set of consistency conditions just provided by the canonical commutation relations. It turns out that the connection between the expansions of the Lorenz gauge potential in terms of the Minkowski modes (73)-(76) and of the Rindler modes (88)-(89) can be neatly obtained according to the method recently developed by Aref’eva and Volovich [16] . Actually, for any real tempered distribution the Mellin transform of its restriction to the real positive half-line is defined by

(90)

which admits analytic continuation to a meromorphic function in the whole complex plane with simple poles at The inversion formula reads

(91)

where and are real positive numbers. A comparison with Equation (89) yields and, in such a manner that for

(92)

Moreover we get

(93)

where use has been made of the Minkowski set (76). From the relation

we definitely obtain

(94)

that eventually yields the relationships between the holomorphic amplitudes of the Lorenz gauge potential on the Minkowskian space and the right Rindler wedge respectively: namely,

(95)

in full accordance with [16] . The above operator transformation (95) leads to the coefficients

(96)

(97)

that yields

(98)

(99)

which actually corresponds to Bose-Einstein thermal distributions at the equilibrium temperature, i.e. the Unruh temperature [4] , being the Boltzmann constant. A quite similar calculation drives to

(100)

where use has been made of the Minkowski set (73). Hence we definitely obtain

(101)

(102)

and thereby

(103)

(104)

5. Conclusion

In this short note we have presented the quantum theory of the lineal, i.e. one dimensional in space, radiation field in a uniformly accelerated reference frame referred to Rindler’s curved coordinates. The pair of physical and nonphysical radiation fields, which must be introduced in a diffeomorphism and gauge invariant quantum theory on a flat space-time, appear to be described by null norm quantum fields, in such a manner that a subsidiary condition must be introduced to select the physical Hilbert sub-space, the quantum states of which are of positive semi-definite norm according to [15] . The Bogoliubov coefficients connecting the inertial and non-inertial Observers have been calculated by means of a new technique due to Aref’eva and Volovich [16] . The result of our calculations turns out to be singularity free and in full agreement with the long standing known expression [4] , which is valid for an ordinary mass-less scalar field. This conclusion allows to set upon a solid and reliable framework the operational analysis of [2] concerning the emission, propagation and detection of the electromagnetic radiation in a non-inertial reference frame.

Acknowledgements

The work has been supported by the Department of Physics and Astronomy of the University of Bologna (DIFA).

Cite this paper

RobertoSoldati,11,CaterinaSpecchia, (2015) On the Massless Vector Fields in a Rindler Space. Journal of Modern Physics,06,1743-1755. doi: 10.4236/jmp.2015.612176

References