Journal of Modern Physics
Vol.06 No.11(2015), Article ID:59587,10 pages
10.4236/jmp.2015.611150
Physics in Discrete Spaces: On Some Cosmological Issues
Pierre Peretto
Laboratory of Physics and Modelling of Condensed Matter, Grenoble, France
Email: Pierre.peretto@lpmmc.cnrs.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 April 2015; accepted 12 September 2015; published 15 September 2015
ABSTRACT
This article is an application of the theory of discrete spaces to cosmology. Its conclusions are necessarily speculative. An interesting aspect is that it gives possible solutions to many pending problems within a unique framework. Let us cite a scenario for the Big-Bang that avoids any initial mathematical singularity, an interpretation of dark matter that does not involve any hadronic matter, a description of the formation of stellar and galactic black holes and, for the later, a description of quasars, their characteristics and their source of energy. Finally dark energy is also given an interpretation through modifications of the laws of gravity.
Keywords:
Big Bang, Dark Matter, Black Holes, Quasars, Bekenstein-Hawking Entropy, Cosmological Constant

1. Introduction
Cosmology is a branch of physics that aims at giving a comprehensive interpretation of the universe as a whole. Theoretical cosmology is based upon General Relativity whose central idea is the introduction of a site-depen- dent metric that is a specific organization of space-time. In preceding articles [1] -[4] , we have introduced another specific type of space-time organization (obviously not at variance with General Relativity); according to which the universe would be made of a set of very simple interacting binary physical units called cosmic bits, a discrete model of space-time must have deep consequences in cosmology. In this contribution, we use the theory of discrete spaces to give possible interpretations of various cosmological pending problems. Some aspects of the present contribution have already been presented in former articles. They are more precisely discussed and gathered in the present paper.
2. On the Big-Bang Paradigm
2.1. The Classical Approach of the Big-Bang Theory
The observation that the galaxies are moving away from one another led to the conclusion that far in the past, some 13.7 billions years ago, the dimension of the universe was extremely small. This conclusion is strongly supported by the theory of General relativity which concludes that the universe is a dynamic system that either expands or contracts. The study of the equations of General relativity shows that they can admit singular solutions indeed: At its very beginning the universe as a whole would be reduced to a single point that is a mathematical singularity.
Most physicists, however, are not pleased with mathematical singularities. To avoid such a situation several remedies have been put forward all based upon the idea that there existed a pre Big-Bang state. Let us cite:
1) The metrics of our space-time is 4-dimensional and Lorentzian. In the pre Big-Bang state it would have been 4-dimensional and Euclidean [5] .
2) A close idea is that time could have been imaginary in the pre Big-Bang state [6] .
3) Finally it has also been suggested that the universe could be cyclic that is a universe with an expansion behaviour following a contraction behaviour [7] .
Another difficulty was found in the observation that the young universe is homogeneous in spite of the fact that its parts could not be related by relativistic causality. The solution, put forward by Guth, is the phenomenon of inflation [8] .
2.2. A Reminder of the Model of Discrete Spaces
According to previous contributions, more specifically in Ref. [1] , the universe is comprised of a countable set of cosmic bits 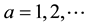 that are very simple physical systems whose states
that are very simple physical systems whose states 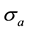 are completely determined by one binary variable
are completely determined by one binary variable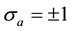 . Cosmic bits are similar to (classical) Ising spins. Is the set of cosmic bits a finite set? Since there is no physical reason to limit its size, the set of cosmic bits is assumed to be infinite but, as we shall see, this does not mean that the observable universe is infinite. The, non measurable, size of a cosmic bit would be of the order of the Planck length, that is
. Cosmic bits are similar to (classical) Ising spins. Is the set of cosmic bits a finite set? Since there is no physical reason to limit its size, the set of cosmic bits is assumed to be infinite but, as we shall see, this does not mean that the observable universe is infinite. The, non measurable, size of a cosmic bit would be of the order of the Planck length, that is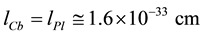 .
.
The cosmic bits interact with each other through random two-body connexions such as 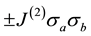 and random four-body connexions such as
and random four-body connexions such as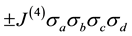 . The universe therefore may be seen as a sort of Ising spin- glass. The interplay between the interactions generates a granular structure whose grains are called world points. A world point is made of
. The universe therefore may be seen as a sort of Ising spin- glass. The interplay between the interactions generates a granular structure whose grains are called world points. A world point is made of 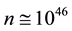 cosmic bits all connected with each others through binary ferromagnetic interactions
cosmic bits all connected with each others through binary ferromagnetic interactions . The size l* of a world point would be of the order of
. The size l* of a world point would be of the order of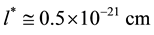 .
.
Finally the system is subject to a degree of disorder whose intensity b is similar to the inverse of some temperature although the meaning of this temperature has nothing to do with ordinary temperature. The role of b is extremely important because b is the driving principle that builds all physical objects, space-time itself [1] , quantum states [2] , fields [3] , and particles [4] . Its role, we shall see, would also be central in cosmology.
To summarize we put forward that the universe may be considered as a ferromagnetic powder (a special sort of spin glass) whose properties can be found by using the classical tools of statistical physics.
2.3. A New Interpretation of the Big-Bang
The ferromagnetic interactions inside a world point generate a polarization 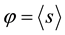 defined by the thermal average of the order parameter s [1] .
defined by the thermal average of the order parameter s [1] .
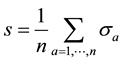 .
.
The polarization 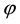 is a solution of the mean field equation:
is a solution of the mean field equation:
 (1)
(1)
where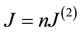 . The polarization
. The polarization 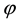 of a world point i may be seen as the length of a d-dimensional vector
of a world point i may be seen as the length of a d-dimensional vector 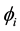

If bJ < 1 the only solution of Equation (1) is


When the polarization 
We are compelled to define the pre Big-Bang as a set of parameters given a priori. This set of parameters has an ontological character that is they do not need further explanations. The parameters are the following:
1) A infinite countable set of binary units.
2) A random distribution of 2-body interactions and 4-body interactions.
3) A noise distribution.
The parameters are generated freely, as in cards deals for example, except for two constraints.
・ There is a correlation between the signs of 2-body 

・ The cosmic parameters 

Since no time has been generated so far we can see the pre Big-Bang state as a state frozen in an eternal present. We can consider either that the present has no beginning and no end, or alternatively that the beginning and the end of the present are one and the same thing. If we adopt the first point of view, that is the universe has no beginning, then there is no room for an act of creation. If we adopt the second point of view, the present, a notion then consubstantial with the pre Big Bang state, can be seen as an act of creation. Which point of view is adopted is a matter of personal philosophy.
2.4. The Very Beginning of the Universe
The states 



Δ is a 





In Ref. [1] we have shown that in spaces devoid of particles one has 

with a metric tensor g given by
c is the, dimensionless, speed of light. It is given by



In the pre Big Bang state, for world points where bJ < 1, the speed of light c is an imaginary number and the metrics is Euclidean as proposed in Refs. [5] and [6] .
Space-time, quantum states, fields and matter spontaneously appear in regions of the pre Big Bang state where bJ > 1. We define our universe as a region of the pre Big-Bang state where 4 < bJ < 5. According to this point of view an infinite number of universes could emerge from the pre Big-Bang state but most of these universes are quite different from ours and entirely out of reach. It must be noted that the speed of light 
3. Dark Matter
3.1. Introducing Dark Matter
At the beginning of the 20th century the astronomical observation revealed an anomaly of the speed of stars rotating around the centre of their galaxies [9] . The observed speed is constant whereas, according to Newton dynamics, it would have to decay as
Obviously the question is to determine the nature of dark matter that is the sort of particles it is made of. Various hypotheses have been proposed such as cold wandering bodies or neutrinos etc. but all these possibilities have been ruled out and most astrophysicists agree today that dark matter cannot be made of hadrons. In other respects Milgrom has proposed another explanation for the rotation anomaly and dark matter seems to be no longer necessary. He suggests that the Newton law of gravitation strength must be modified along the following formula
with 



G is the gravitation constant and rM is the Milgrom parameter [3] . This is the MOND theory (for Modified Newton Dynamics). The agreement with observation is striking and rather convincing and it seemed that dark matter could be ignored. That is not the case.
The gravitation forces are, in the MOND theory, exactly known. They are central and enable an exact calculation of the motions of galaxies in a cluster of galaxies to be carried out. The observation of the galaxy cluster 1E0657-56 (the Bullet) does not support the calculations. Dark matter is still necessary to explain the observation and also, for example, to account for the formation of galaxies.
Moreover the Milgrom interactions have no observable effect upon the geometry of space-time whatsoever and cannot explain the observed maps of dark matter. Besides its unknown nature dark matter gives rise to other problems. For example it seems that there is no dark matter in our solar system whereas the solar system is placed right inside the disk of the Milky Way where dark matter must be present.
3.2. A New Interpretation of the Dark Matter
The model of discrete space-time that we put forward may provide an alternative interpretation.
Let us consider the metric matrix of vacuum (Equation (4)). This matrix is sensitive to variations of cosmic noise b and since the speed of light is given by 


4. Black Holes
4.1. Two Sorts of Black Holes
Black holes are regions of our universe where the Lorenz metrics is strongly modified or even disappears altogether. These objects have been experimentally observed, not directly because they are invisible, but through their gravitational effects. Two types of black holes have been identified.
・ The stellar black holes with masses of the order of 15 Sun masses. Their presence is revealed by the motion of binary stars where a star orbits around a point associated with no visible object.
・ The galactic (or super-massive) black holes that are placed in the vicinity of the centres of galaxies. Their presence is revealed by the simultaneous motions of numerous stars orbiting around a point still associated with no visible object. The masses of galactic black holes are enormous. The galactic black hole of the Milky Way, our own galaxy, is called Sgr A*. Its mass exceeds several millions Sun masses but galactic black holes with masses higher than several billions Sun masses are observed in the distant universe.
Black holes give rise to many questions such as:
1) Are stellar black holes and galactic black holes two aspects of the same physical object?
2) What is the mechanism of their creations?
3) What is the nature of the matter they are made of? etc.
The model of discrete spaces that we propose may give possible answers to these questions.
4.2. Stellar Black Holes
The solution, by Schwarzschild, of the equation of General Relativity in spherically symmetrical systems shows that the space-time metrics is singular at a distance given by 
・ A first step that we find in ordinary stars, such as in the Sun itself, is the dissociation of electrons from their nuclei. This state of matter is called plasma.
・ In stronger gravitational fields the components of nuclei, protons and neutrons dissociate in turn and give rise to a new state of matter, a quantum gas with about one electron for one neutron and one proton. This is the material the white dwarfs are made of.
・ The next, and up to now the last, step is the absorption of electrons by the protons. Matter is then entirely made of neutrons. This is the material the neutron stars (or pulsars) are made of.
The existence of stellar black holes seems to require another step in the transformations of matter that is the transformation of particles of the Standard Model themselves. In Ref. [4] we have proposed a structure of the elementary particles that accounts for most of the properties of the Standard Model. In this model the elementary particles are built around specific world points, called the seeds of the particles whose internal spaces display their symmetry. For large enough densities the effect of 4-bodies interactions 
To make this discussion more complete let’s have a look at the “no-hair theorem”.
If we merge Q world points together, the polarization 
In stellar black holes Q is a large number that is
In other respects the polarization is a solution of the mean field equation
For the components to have a physical meaning it is necessary that
This determines the internal dimensionality of a stellar black hole:
Since Q is generally a very great number, the internal dimensionality of a stellar black hole, if not infinite, is extremely large which means that the notion of dimensionality loses, in actual fact, its meaning.
The polarization component 



The cosmic noise b into a stellar black hole tends towards the cosmic noise of its surrounding, that is 

According to our interpretation a stellar black hole would be similar to a “hairy”, hollow, 
Seen from the outside a stellar black hole seems to be a no-universe region that stretches the fabric of surrounding ordinary space-time so giving rise to the observed gravitational effects. Moreover the transformation of ordinary matter into black holes amounts to a simple reorganization, not a vanishing, of its degrees of freedom. Therefore, in our interpretation, the entropy of a black hole remains finite and the physics of a stellar black hole is no more in contradiction with the second principle of thermodynamics. This approach also suggests a new derivation of the Bekenstein Hawking entropy formula:
Let A be the surface of a stellar black hole. Since the size of a cosmic bit is of the order of the Planck length, the number 






Finally the black hole entropy is given by
a formula close to but not identical to the Bekenstein formula [10] .
4.3. Galactic (Super-Massive) Black Holes
Is the nature of galactic black holes similar to the nature of stellar black holes, that is, do these two objects only differ by their sizes? The classical interpretation is that stellar and galactic black holes are the same objects indeed and that galactic black holes are built by stellar black holes that swallow more and more ordinary stars.
If correct this idea leads to the conclusion that the older a galactic black hole the larger it is. This conclusion is not supported by the observation. The largest galactic black holes are, by far, observed in the very distant (young) universe We are therefore compelled to imagine that the galactic black holes are objects closely connected to the Big-Bang itself.
Let us consider a region, that we shall call a galactic black hole, in the pre Big-Bang state (defined in Section 2.3) where bJ < 1, surrounded by a region where 4 < bJ < 5. In this region, because bJ < 1, there is no space-time, no fields and no particles. After the transformation that follows the Big-Bang has been completed we have a universe similar to our universe surrounding a no-universe region, a region where no space, no time, no fields and no particles can exist. This region is, along our point of view, a galactic black hole. For the very same reason that makes a stellar black hole deforms its surrounding space-time, a galactic black holes creates a strong gravitational field in its vicinity.
To summarize we think that stellar black holes and galactic black holes are different objects. Their main difference is in the dimensionality dbh of their internal spaces, extremely high dimensionality for stellar black holes

5. Quasars
5.1. Generalities
Quasi-stellar radio sources (or quasars) are the brightest objects of our universe. The energy they pour in space is so enormous that it is difficult to imagine a process based upon ordinary physics that could account for the phenomenon. The observation shows that these objects are closely related to galactic black holes and it has been put forward that the quasar energy could be generated by the disintegration of stars falling in the hole. The quasar energy would originate from the energy imbedded in the remains of the stars in a spherical region placed at about 103 rS (Schwarzschild radius) from the centres of galactic black holes.
There are arguments that go against that scenario. For example there exist quasars not related to any galaxy. They are called “naked quasars”, HE0450-2958 is an example [11] . There also exist quasars associated with galaxies housing sparse stars populations. Another model seems to be necessary.
5.2. A New Interpretation of the Physics of Quasars
An observational important feature is the fact that quasars mainly exist in the very distant universe. Their absence in the vicinity of our galaxy is generally simply explained by the lack of stars in the centres of old enough galaxies such as our Milky Way. Another interpretation, distinct from the fall of stars, is possible. Since galactic black holes seem to be the result of a process closely related to the Big-Bang we can assume that so is the case of quasars. Quasars would the manifestation of the phase transition (a transformation) of a part of the world points belonging to a galactic black hole (where bJ < 1) into world points belonging to our universe (where bJ > 1). This process would result from a local equalization process of cosmic noises b between the (hot) galactic black hole and our own (cold) space-time. The equalization process proceeds at the spherical boundary of the galactic black hole. According to this interpretation a quasar would be a region where space-time, fields and particles are created: Far from being a trap for matter a quasar would be a source of matter instead. Quasars, according to our opinion, would be the genitors of galaxies. There are indications that the quasars are older than galaxies [11] , that galaxies housing large galactic black holes have more stars. Also HE0450-2958 seems to feed the galaxy it is linked to [12] . Finally the very far away quasars are hidden behind clouds of dust [13] , an observation that could be explained by the emission of newly created matter by quasars.
According to this interpretation the size of a galactic quasar must decrease with time but the erosion process is not necessarily continuous. A galactic black hole, a region of space where bJ < 1, can possibly house regions where bJ > 4. When the boundary of a galactic black hole reaches such a region the erosion process stops and the galactic black hole becomes silent. So could be the case of Sgr A*. Some faint activity could remain, however, with the possible production of electron-positron pairs; a phenomenon that has been observed.
The tremendous energy released by quasars also receives a new interpretation. We have seen in Ref. [3] that the intensity of gauge interactions, electroweak and strong, is determined by the parameter


energy 

tation forces which is of the order of 
6. Dark Energy
6.1. A Non-Vanishing Cosmological Constant
The measurements of the luminosity of distant supernovae show that their host galaxies are farer than the position predicted by the usual universe expansion. Some repulsive interaction between the galaxies seems to be at work [14] . The introduction of a very weak cosmological constant 

6.2. A Model of Gravitation
Some arguments that we develop in this section have already been discussed in Ref. [3] .
In molecules the centres of gravity of positive and negative charges are generally different so giving rise to fluctuating electric dipoles. The dipoles interact and some dipole orientations lower the energy, the closer the systems the larger the energy lowering. The result is an attractive force, the so called Van der Waals interactions. The nuclear forces are also attractive and also arise from fluctuations, the fluctuations of quarks colours.
Since the classical gravitation interactions is attractive we put forward that gravitation could arise from the coupling between fluctuations, the fluctuations of the world point polarization







If 







To Q, another (probe) particle, with mass m we associate a fluctuation
Then, owing to the weakness of vertices, the interaction may be calculated by using a low order perturbation expansion. The lowest order writes
The static 
The Fourier transform of 



The Newton expression of attractive gravitational forces is recovered:

We observe that G behaves as


of the order of 


stated in Section 5.2.
6.3. Milgrom Interactions and the Cosmological Constant
The dimensionality of the internal interaction matrix 





If the fluctuations of one component 



where 
Then by letting 
Since d = 4 we find

The form of the gravitation interaction associated with (2 + 1)-dimensional world points is modified because the Fourier transform of 
Finally this gravitational forces is attractive and given by

The Milgrom gravitation interaction is recovered (Section 3.1) and the gravitation interaction becomes
with




The disappearance of a dimension may be interpreted as the shrinking of the lengths associated to that dimension by a factor

A world point i eventually loses another dimension if the fluctuations perturb simultaneously two field components 



The associated gravitation force is
a repulsive constant force that acts as a negative pressure exactly as does the cosmological constant.
The formula gathering all various contributions to the gravitation forces is
In this equation 
Since the motion of stars in the disks of galaxies is determined by the Mond dynamics the Milgrom parameter rM must be of the order of, or less than, the galactic bulbs radii. The galaxy bulbs diameters 

Since the distance travelled by light in one year is





7. Discussion and Conclusions
The present paper is the last of a series of five articles devoted to the physics of discrete spaces. The purpose of preceding contributions was to show that a simple spin glass model could account for the most fundamental constructions of theoretical physics, namely the structure of space-time [1] , the postulates of quantum theory [2] , the gauge interactions [3] , and the Standard Model of Particles [4] . Here the purpose is quite different: one uses the model to put forward an explanation to not completely understand phenomena in the field of cosmology. So is the case for the scenario of the Big-Bang, the nature of dark matter, the physics of black holes and a more detailed description of quasars.
Could the model of discrete spaces be falsified, a necessary condition, according to Popper, for a theory to deserve the adjective “scientific”?
The model is based upon three very simple and general statements that we cannot reject without jeopardizing physics itself: The universe does exist, it is not completely chaotic and it is not completely frozen. We could negate the model but this would lead to a rebuttal of at least one of well established theories. Therefore, it is difficult to say that the theory of discrete spaces that we put forward can be falsified on the account of the first four articles. This is not the case for the present contribution. For example our proposal leads to the conclusion that the search of dark matter particles is hopeless because dark matter is not made of matter. If such particles are found some aspects of the theory would have, obviously, to be revised. We think that the touchstone of the present model is in the nature of quasars because quasars are, in our approach, to be considered as the still active embers of the Big-Bang.
Acknowledgements
I would like to thank Pr Aurélien Barreau for the useful discussions we have had as regards the Pioneer effect.
Cite this paper
PierrePeretto, (2015) Physics in Discrete Spaces: On Some Cosmological Issues. Journal of Modern Physics,06,1456-1466. doi: 10.4236/jmp.2015.611150
References
- 1. Peretto, P. (2014) Journal of Modern Physics, 8, 563-575.
http://dx.doi.org/10.4236/jmp.2014.58067 - 2. Peretto, P. (2014) Journal of Modern Physics, 14, 1370-1386.
http://dx.doi.org/10.4236/jmp.2014.514138 - 3. Peretto, P. (2014) Journal of Modern Physics, 18, 2049-2062.
http://dx.doi.org/10.4236/jmp.2014.518201 - 4. Peretto, P. (2015) Journal of Modern Physics, 6, 811-828.
http://dx.doi.org/10.4236/jmp.2015.66086 - 5. Hartle, J.B. and Hawking, S. (1983) Physical Review D, 28, 2860.
http://dx.doi.org/10.1103/PhysRevD.28.2960 - 6. Wick (1956) Physical Review, 101, 1830.
- 7. Steinhardt, P.J. and Turok, N. (2004) New Astronomy Reviews, 49, 2-6.
- 8. Guth, A. (1982) Physical Review Letters, 49, 1110-1113.
http://dx.doi.org/10.1103/PhysRevLett.49.1110 - 9. Tayler, J. (1991) Hidden Matter. Elis Horwood, Chichester.
- 10. Bekenstein, J.D. (1975) Physical Review D, 12, 3077.
http://dx.doi.org/10.1103/PhysRevD.12.3077 - 11. Tista, M. (1975) Physics Letters B, 561, 53-56.
http://dx.doi.org/10.1016/0370-2693(75)90497-9 - 12. Elbaz, D. (2009) Astronomy and Astrophysics, 507, 1359-1374.
http://dx.doi.org/10.1051/0004-6361/200912848 - 13. Margain, P. (2005) Nature, 437, 381.
http://dx.doi.org/10.1038/nature04013 - 14. Peebles, P.J. and Ratra, B. (2003) Reviews of Modern Physics, 45, 559-606.
http://dx.doi.org/10.1103/RevModPhys.75.559





















