Received 3 March 2015; accepted 2 April 2015; published 3 April 2015

ABSTRACT

As defined and used in General Relativity calculations, spacetime is a strictly classical construct which does not incorporate in any way, shape or form the concept of quantum. While reviewing the efforts that Alexandria theoretician M. S. El Naschie has made to resolve the dichotomy, we discovered that his E infinity theory contains a Cantor set which has characteristics specified by Isaac Newton for Absolute space. We show that this unexpected connection leads to an understanding of the mysterious origin of the one and only attribute that all particles listed in the Standard Model of Elementary Particles possess―including notably the photon―and which has remained unexplained hitherto: spin. This most rewarding result reinforces our belief in the relevance of the E infinity basic concepts in relation to our own Xonic Quantum Physics (XQP) which places dynamical action rather spacetime and energy at the core of the System of the World.

Keywords:

Quantum Foam, E Infinity, Xonic Quantum Physics, Newton, Absolute Space, Photon Spin

1. Introduction

In 1955, renowned General Relativity (GR) expert Archibald John Wheeler, then at the top of his talents, had a brilliant idea. Perhaps, he said, at the subatomic level GR spacetime has the consistency of “a foam”―a quan- tum foam―forming the foundation of the fabric of the universe [1] . Now it happens that GR spacetime is a strictly classical construct which does not incorporate in any way, shape or form the concept of quantum―an intolerable shortcoming.

There was a simple way out of the difficulty: give up GR spacetime and replace it by something having the quantum concept built in from the start. But, as the French like to say in situations such as this: “Pourquoi faire simple quand on peut faire compliqué―Why make it simple when one can make it complicated?”

John Wheeler chose his own (complicated) way out of the dichotomy. Quantum foam does occur in spacetime, he said, but only at the “Planck scale” level―in brief, turbulences occur in spacetime, but at extremely small scales of space and time only―forming “mini black holes” (the expression “black hole” was invented by Wheeler).

The strenuous efforts GR theoreticians have engaged ever since to render GR compatible with the require- ments of Quantum Physics (QP) suggest that 1) either nature is extravagantly complicated―at least at the “Planck scale” level; or 2) that physics―at least GR physics―has gone astray somewhere along the line.

In a series of recent extensive publications, Alexandria theoretician Mohamed S. El Naschie has attempted to resolve the GR-QP dichotomy on the basis of a body of original proposals he calls E infinity. Resuscitating in his own words John Wheeler’s idea of the quantum foam, he explained: “On extremely small scales, at very high observational resolution equivalent to a very high energy, spacetime resembles a stormy ocean”, adding: “The crucial step in E infinity formulation [is] to identify the stormy ocean with vacuum fluctuation and in turn to model this fluctuation using the mathematical tools of non-linear dynamics, complexity theory and chaos [2] ”.

Following in M. S. El Naschie’s footsteps, we showed that his scheme leads logically to the consideration of a System of the World in which two active principles, we call the Xon and the noX, discontinuously construct and deconstruct space lengths and time lapse durations―i.e. some forms of quantized strings―generating in the process in the Void two kinds or species of points, i-points and e-points [3] .

If the System of the World thus constructed corresponds to Reality, then some probing questions which cur- rently perturb our understanding of what Quantum Physics is all about become answerable.

2. Following a Sinuous Path

One of the most haunting unresolved questions in modern QP can be stated quite simply: why do all the particles officially listed in the Standard Model of Elementary Particles (SM) carry a spin? What are the nature and the origin of this singular attribute?

We endeavor to address this probing question in the present Note. We’ll do it by following a sinuous path ―which relates in fact to the indirect road we took in search of an answer.

We begin by redefining succinctly the dichotomy which historically has set GR apart from QP. We then ex- amine the remarkable efforts Alexandria theoretician Mohamed S. El Naschie has made to resolve the dichoto- my. Following in his footsteps; we review our own invention of the System of the World we call Xonic Quan- tum Physics (XQP).

In so doing we came upon an amazing discovery: M. S. El Naschie’s E infinity theory hides an hitherto un- suspected structure which makes it possible to comprehend perhaps the nature and the origin of spin―and of the photon spin in particular―a most rewarding result.

3. Setting up the Stage

Consider the Topological Unit Line Segment (ULS) (0, 1). Remove figuratively ALL the points it contains. We shall call the empty frame which is left behind when the deconstruction process has been completed, the Void. We shall say further that QP is the attempt to fill the Void thus constructed with a content apt at representing with some success the inner (hidden) functioning of the System of the World―Nature.

In the context of QP as it is conventionally practiced today, the Void is said to be filled with a continuum commonly called Spacetime. We showed in [3] how this appellation came into being as the result of an errone- ous evaluation of the true nature of the invention made by French genius mathematician (and theoretical physic- ist) Henri Poincaré in 1905 when he constructed the mathematical device he called, and we still call today, the Lorentz transformation, which forms the core of the theory of Relativity. The premature death on January 12th 1909 of the German mathematician Hermann Minkowski has fossilized the prediction he made four months be- fore his death when he asserted foolishly: “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality”.

“Are doomed”, assured Minkowski. In fact, space and time have not faded away―quite to the contrary; but the appellation Spacetime has survived and is haunting QP ever since with devastating consequences.

4. Filling the Void

4.1. With a 4-Dimensional Spacetime

In June of 1913, Albert Einstein assigned himself the (difficult) task of constructing a (mathematical) spacetime capable of responding to the presence of masses and/or energy in its midst. Meeting with difficulties, Einstein addressed to his friend, the brilliant Swiss mathematician Marcel Grossmann, a call for help: “Grossmann, Du mustmirhelfen, sonstwerd’ ichverrückt!”―Grossmann, you must help me or else I’ll go crazy! [4] .

In response, Grossmann pointed to a spacetime dotted with a Riemannian geometry in four dimensions.

4.2. Without a Dimensional Spacetime

A century later―almost day for day―Alexandria theoretician Mohamed S. El Naschie published a paper which became the most popular―the most read―paper ever published in this journal. In his Introduction M. S. El Naschie states: “We start by considering a line segment representing a unit interval, which in turn represents a one-dimensional idealized spacetime” [5] .

As we pointed out in [3] , the fact that the Topological Unit Line Segment can be used to represent “a one- dimensional spacetime” is a rigorous consequence of the outstanding theorem discovered in 1874 by the Founding Father of Set Theory, Saint-Petersbug born German mathematician Georg Cantor, who proved that for any positive integer n, there exists a 1-to-1 correspondence between the points on the ULS and all of the points in an n-dimensional space.

In undertaking his project, Pr. El Naschie rid himself of the (historical) necessity of assigning four dimen- sions―or more―to spacetime: “In E infinity theory, he explained, we admit formally an infinite dimensional “real” spacetime [our emphasis]”. However, he added, “we were able to show that although E infinity has for- mally infinitely many dimensions, seen from a distance, i.e. at low resolution or equivalently at low energy, it mimics the appearance of a dimensional spacetime manifold which has only four dimensions”, concluding: “Thus the four-dimensionality is a probabilistic statement, a so-called expectation value”.

Mohamed S. El Naschie thereby established a connection between the concepts of Dimension and Probability.

The flexibility of E infinity with regard to dimensionality represents an advantage of deep significance: it makes it possible for E infinity to deal equally well with spacetimes of all dimensions: Grossmann-Einstein (4); Kaluza-Klein (5), Superstring theory (10), String theory (26), or Heterotic string theory (4, 6, 10, 16, 26).

5. On M. S. El Naschie’s Daring Use of the Golden Ratio

Mohamed S. El Naschie has constructed his E infinity theory around a remarkable set theoretical discovery he introduced in these words: “There is a well known theorem due to Mauldin and Williams which states that with a probability equal to one, a one dimensional randomly constructed Cantor set will have the Hausdorff dimension equal to 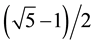= 0.618033”, i.e. the golden mean ¢ minus 1.

The golden mean, also called the golden ratio, is a pure number dotted with outstanding properties, one of which is the fact hat it is “the most irrational” of all the irrational numbers presently known in Number theory. It can also be constructed geometrically [6] . Figure 1 proposes one method which shows (which suggests) that the golden ratio might bear some hidden relation with the equally irrational number π of plane geometry. M. S. El Naschie’s use of the golden ratio in E infinity is one of the secrets of its successes. Inspired by this example, we looked for connections in a different―in opposite―directions. We found a surprising link.

AS/SB = ¢ =.

6. The Xonic System of the World

In our scheme, the deconstruction of the ULS is a physical process performed by the noX rather than a purely mathematical device. There is every reason to assume that this physical process occurs randomly. If this is the case, then consequences will ensue which might be of considerable significance. Let us examine what they are likely to be.

Suppose the noX sublimates (effectively removes) the points located on the interval (a, b) which it selected randomly―one might say accidentally―on the ULS. This “accidental” deconstruction sublimates (scatters) the points belonging in the segment (a, b), which become thereby i-points as per our terminology, while leaving untouched the points a and b, which become e-points, as well as the points belonging to the two segments (0, a) and (b, 1) left untouched, so far. Again, the noX selects―randomly―on these untouched segments new segments to sublimate off, and so on ad infinitum. An amazing theorem known as the Mauldin-Williams theorem shows that the random Cantor set thus generated has a Hausdorff or fractal dimension equal to the inverse of the golden ratio, 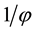[7] .

This is in accordance with the select iterative deconstruction process that M. S. El Naschie has described in detail in [5] . This particular process introduces the golden ratio quite naturally in the theory, a fact which makes all the difference in the world. Any other choice would have yielded an altogether different result and we would not have been in a position to write the present Note. For this reason, we shall stop here briefly to review what is involved.

7. Xonic Little Bangs Generate Space Lengths and Time Lapse Durations

According to our terminology, as the noX deconstruction of the ULS progresses, it generates a substrate made up of i-points which bear no geometric relations of proximity or distance with each other. The deconstruction leaves behind e-points which remain at the precise positions (relative to each other) they occupied on the ULS before the deconstruction occurred. Counterpart to the noX, the Xon intervenes in the substrate, generating space lengths and time lapse durations made up of i-points borrowed in the substrate. Each of these lengths and durations constitute a new ULS in its own right, therefore subject to noX iterative deconstructions which yield more i-points and leave behind more e-points, a discontinuous process we have called “Xonic little bangs”, which fares well with M. S. El Naschie’s concept of a “stormy ocean” subject to “vacuum fluctuations”.

Even though they are not connected with each other by geometric relations―they do not form continuous segments or curves, for example―e-points bear relations of order with each other. This forms the basis for an unexpected connection with a concept supposed to have been abandoned by physicists once for all a long time ago―which we shall presently resurrect.

8. The Hidden Geometric Structure of the e-Points Set

Taken together, our i-points form a Cantor set which El Naschie has called the Empty set. It constitutes for us a substrate, e-points form a Cantor set that El Naschie has named the Zero set. This set is dotted, by our reckon- ing of a structure. As we shall presently demonstrate, this structure qualifies under specifications formulated three centuries ago in a section of the Scholium that Isaac Newton placed at the beginning of his treatise, written in Latin, the illustrious Philosophiae Naturalis Principia Mathematica. In Section II of this Scholium, Newton alludes to the presence in Nature of an entity he calls Spatium absolutum―Absolute space―which he defines in these terms: “Spatium absolutum […] manet similar & immobile―Absolute space remains similar (i.e. un- changed) and immovable [our translation] [8] ”.

This is precisely the case of our e-point set―El Naschie’s Zero set. Taken together, the points it contains form a structure which remains unchanged and is immovable.

There is something else.

9. On Newton’s Prudent Use of the Word Mathematica in His Principia

Newton in his early days took an interest in Number theory―he performed calculations for example, using the esoteric Pascal triangle. But he does not seem to have paid special attention to the golden mean or to its potential significance―even though his great predecessor Johannes Kepler did―as well probably as a number of his secret correspondents in Alchemy (Figure 2).

Newton did not possess either our concept of Energy (E) nor the concept of a “gravitational constant” (G).

He did well without them. To construct his System of the World―to him essentially the Solar system―he forged concepts derived from the alchemical and the theological (biblical) investigations that he continuously carried out in the secrecy and the privacy of his rooms in Trinity College at the University of Cambridge.

Weary of using openly in his writings the word Alchymia―borrowed from the Arabic al-kīmiyā’ (الكيمياء‎), Alchemy to us today―Newton resorted to a clever trick: he replaced this word in his writings―including in his treatise’s title―by the innocent-sounding Latin word Mathematica―and everybody has fallen for it ever since (Figure 3).

Newton’s Definition V, which he placed before the Scholium in his Principia, is instructive in this regard.

10. Decoding the Hidden Meaning of Newton’s Definition V

10.1. Definition V

Its title reads:

Def. V.

Vis centripeta est qua corpus versus punctumaliquodtanquam ad centrum trahitur, impellitur, velutcunq; tendit.

In the physics textbooks published around the world since the parution of the Principia, this definition is conventionally translated as: “The centripetal force is that by which bodies are drawn, impelled, or tend in some manner from all sides towards some point, as towards a center”.

Newton’s choice of the word Vis which appears in this title is commonly translated as Force in English and in French, Kraft in German, 力 in Chinese and Japanese, Fuerza in Spanish, силы in Russian, 힘 in Korean…

These translations carry the true meaning of the word Vis―as used by Newton―only if they are understood to refer to an active principle―to a “Power” or to a “Virtue”―acting on (in) the physical body (corpus) concerned.

As for the word Punctus… it corresponds to the words Point in English and in French, 포인트 in Korean, 点 in Chinese (simplified), ? in Chinese (traditional), Punkt in German, Punt in Dutch, Iphuzu in Zoulou, Nokta in Turkish, Tочка in Russian, Ponto in Spanish, Punto in Portuguese…

In reality however, just as for the word Vis, Punctus in all its declinations―as used by Newton―carries hidden connotations.

10.2. Newtonian Centers Are Mathematical Points

In his Definition V, Newton introduces an alchemical concept under the designation Vis centripeta. Refraining from saying explicitly what the concept refers to, he describes the effect this Vis centripetal induces when it “acts” on a physical body―a corpus.

His lengthy explanation reveals his firm belief in the presence in Nature of entities he calls Centris―Centers to us today―which are “mathematical points”―quæsunt puncta Mathematica. He gives telling examples of the way these Centers function in Nature (our translation, our emphasis): “Of this sort is gravity, by which bodies tend to the centre of the earth; magnetism, by which iron tends to the center of the loadstone; and that force, whatever it is, by which the planets are continually drawn aside from the rectilinear motions, which otherwise they would pursue, and made to revolve in curvilinear orbits”.

In the context of the present Note, it is fascinating to realize that―in contradiction with what is conventionally said and taught about Newton’s Universal Gravitation theory―a body which falls toward the ground on the Earth is, by Newton’s recognition, actually drawn toward the Earth Center, which is a “mathematical point”― understand, which has alchemical powers! Similarly―by Newton’s account―the Sun “as a whole” does not cause the planets to orbit around it; a mysterious Ccnter hidden somewhere in its midst does the trick. If one adds to these considerations Robert Hooke’s notion of a Power or Virtue acting on planets in proportion to the inverse square of their distance from the Sun, one has a System of the World which reproduces accurately the laws discovered by Johannes Kepler for the Solar system.

There is no escape possible: our e-points form a structure which has characteristics attributed by Newton to Absolute space―with at least one significant difference, however: this structure does not form a continuum, as Newton’s Spatium absolutum presumably does (even though Newton never explicitly said so).

Let us now look in the other direction and ask this question: where do our e-points come from?

11. Discovering an Unsuspected Structure in El Naschie’s E infinity

In undertaking to find interconnections between E infinity and our XQP scheme, we shall not be shy to call upon recommendations made by Newton in an unpublished manuscript known today as A Treatise on Revelations [9] . In Section 1.1 [8] of this manuscript, Newton urges his readers “to choose those constructions which without straining reduce contemporary visions to the greatest harmony of their parts”. He explains why: “For the design of collaterall visions is to be a key to one another & therefore the way to unlock them without straining must be fitting one to the other with all diligence & curiosity”, adding: “Truth is ever to be found in simplicity, and not in the multiplicity and confusion of things”.

In our scheme, the ULS representing the E infinity spacetime(s) is permanently subjected to noX deconstruc- tions which yield i-points and e-points in the Void. Taken together, the e-points form the Cantor set that Mohamed El Naschie has called the Zero set. Our analysis brings to light one characteristic of this set which may have hitherto gone unnoticed. In brief, being made up of e-points, the Zero set constitutes an Absolute Space in the Newtonian sense of the word―a most stunning result, which makes it possible for us to resolve at least one outstanding unresolved mystery of Quantum Physics.

Before we proceed to examine this unresolved mystery, let us pay attention to another characteristic of the Zero set. By the Mauldin-Williams theorem M. S. El Naschie has alluded to, being constructed randomly the Zero set has a fractal dimension equal to the inverse of the golden ratio, 1/φ, which―by the magical powers of the golden ratio―is equal to 1―φ, formula which yields the approximate value 0.6180…, which corresponds to a fractal dimension less than 1, precisely as one would have expected intuitively. And so, the Absolute space that this structure constitutes is of a very special kind indeed―something rather fascinating and assuredly worth exploring further.

Let us pursue our search of hidden connections between E infinity and XQP on the one hand, and convention- al QP, on the other.

As we pointed out in [10] , the so-called “elementary particles” listed in the Standard Model (SM) of Elemen- tary Particles―the photon is one of them―have all in common one―and only one―attribute: they are said to carry an intrinsic angular momentum, the spin. No one―none of the great names of Quantum Physics―has yet been able to describe what if anything is actually “spinning” in the elementary particles.

Let us consider at close range the particular case of the photon to see what is involved.

12. The Photon Puzzle

12.1. Inventing the Photon

The elementary particle we call today the photon was invented officially in 1905 by Albert Einstein, then work- ing as an Expert Third Class in the Swiss Patent Office in Bern. He introduced it in these words (our translation, our emphasises): “According to the assumption considered here, when a light ray starting from a point [Punkte] is propagated, the energy [it contains] consists of a finite number of energy quanta [Energiequanten] localized on space points [Raumpunkten], which move without dividing, and which can be absorbed or emitted only as a whole” [11] .

(For the detailed story, see our § 12.3 and 12.4 below).

Einstein did not realize it then, but there is something very wrong with this invention.

12.2. Indeed

In 1932, Indian physicists Chandrasekhara Venkata Raman and Suri Bhagavantam, then doing research at the Indian Association for the Cultivation of Science in Calcutta (IACS), published a paper at the end of which they drew this conclusion: “The light quantum possesses an intrinsic spin equal to one Bohr unit of angular momen- tum” [12] .

This assertion raises uncongruous questions concerning the photon―such as these.

Photons are said to be massless and to carry no electric charge. Furthermore, at least according to Einstein, they are said to be localized on space points [Raumpunkten].

Very well then, how can such presumably dimensionless “points” be dotted with a spin―be spinning?

Let us briefly review what is commonly said about the spin in standard physics textbooks.

“Spin is the quantity of rotation of a particle around its axis”.

Photons sit on space points―yet they should have an axis around which they can rotate about?

“A particle rotating to the left has an upward spin, a particle rotating to the right a downward spin. The amount of spin direction we call polarisation”.

Photons do not have poles, how could (can) they be “polarized”…

In view of these questions, one may ponder why the photon was invented in the first place.

12.3. The Photon―Reality or a Fata Morgana Mirage? How Max Planck Led Einstein Astray (Unvoluntarily) in 1905

In Bern, in the spring of 1905, Einstein is living a fastidious life, reviewing eight hours a day patent applica- tions often awkward or poorly written―not exactly the kind of life he had been dreaming of (Figure 4).

One day, he remembered two papers that the Founding Father of Quantum Physics, Max Planck, had published in rapid succession four years earlier, introducing new theoretical concepts. Einstein knew of the existence of these papers for a simple reason: by coincidence, the first paper that he, Einstein, had ever written and submitted for publication in a scientific review (this one, on the subject of capillarity) had been published in the prestigious Annalen der Physik in the same Issue as the two Planck papers we just mentioned―. Einstein’s paper as n° 5 in this Issue (pp. 513-523, received Dec. 16, 1900), Planck’s papers as n° 9 (pp. 553-563, received January 7, 1901) and as n° 10 (pp. 564-566, received January 9, 1901) in the same Issue. If only for sentimental reasons, Einstein had kept a printed copy of the precious Issue which, after all, contained his first scientific publication―in these days published papers were not available “on-line” as they are today.

With the competent advice and support of his brilliant young wife, Mileva Maric-Einstein, and of his equally brilliant good friend and coworker Michele Besso, Einstein reviewed the Planck papers. Two key expressions

Planck had used in these papers soon caught his attention… In the first of the two papers, Planck asserts that the energy that light transports―at least in the case of light in the form of monochromatic radiation emitted by black bodies―is dispersed (travels) in the form of Energieelementen―energy elements. Einstein undertook to make this invention his own by writing a new paper―it would be his second and he would receive the Nobel Prize for Physics for it fourteen years later.

In the second Planck paper, shorter than the first, Einstein encountered another novel expression, unheard of until then, that Planck had used, forming a single expression: the composed word Elementarquantum―elemen- tary quantum. Ironically, Planck forged it to designate… the unit electric charge supposedly carried by… Elek- trons―Planck’s full expression is Elementarquantum der Elektricität.

Very well, but why quantum?

12.4. Quantum Satis

To make a long story short… In 1877, at age nineteen, Max Planck spent a year of study in Berlin with mathe- matician Karl Weierstrass and physicists Hermann von Helmholtz and Gustav Kirchoff. Now it happens that, even though he became mostly famous for his research work as a physicist. Hermann von Helmoltz was, by formation, a physician (physiology). On one occasion or another, Planck learned from him a Latin expression commonly used by physicians at that time when they wrote a medical prescription. To indicate the proper amount (quantity) of a given medication that should be used, they would specify Quantum satis, meaning: “Add as much of this ingredient as is needed to achieve the desired result, but not more”.

Quantum satis… Interestingly, passim, the European Community uses this very same expression today in its directives concerning food regulations and food safety.

By von Helmholtz’s own admission, the first one to use the word quantum in a physics context was the phy- sician (turned physicist like himself) Julius von Mayer (1814-1878) who, said Helmholtz, used the word in a letter dated July 24, 1841. Mayer had discovered the mechanical equivalent of heat and had enunciated that year one of the first versions of the first law of Thermodynamics. He nearly committed suicide when his discoveries were attributed at first to someone else (James Joule). He spent some time in a mental institution to recover from the shock.

The rest is legend: Einstein assigned new names to the Planck Energieelement, calling it notably Lichtquan- tum―quantum of light. It became the photon in 1926 under the pen of the American physical chemist Gilbert Newton Lewis, who justified the chosen name in these words: “I therefore take the liberty of proposing for this hypothetical new atom, which is not light but plays an essential part in every process of radiation, the name photon”.

In inserting the term element in his designation Energieelement, Planck had misled himself and by ricochet, he misled Einstein, four years later. The point is that the energy that the so-called energy “element” is supposed to carry can assume any value from 0 to ∞―it is not quantized. In brief, the Energieelement is not an element in the proper sense of the term. Einstein made the situation worse in calling it a quantum (in Sections 7 and 8 of his paper, he coined the designations Energiequant, Lichtquant and/or Lichtenergiequant).

In fine, when everything has been said, one is faced with a simple truth: the invention of the photon appears to have been the result of a Fata Morgana mirage―(unusual and complex form of superior mirage that is seen in a narrow band right above the horizon)―rather than the description of a Reality.

Let us see how we might be able to remedy this puzzling state of affairs.

13. M. S. El Naschie’s Zero Set Is at Rest in the Void

Let us return to the fact that the particles listed in the Standard Model (SM) of Elementary have all in common one―and only one―attribute: they are said to carry an intrinsic angular momentum, the spin.

In the spirit of the present Note, there is no mystery. The two active principles in our scheme, the Xon and the noX, each carry an elementary quantum of dynamical action which has the dimension of angular momentum.

Now the very concept of angular momentum is meaningless unless it is referred to a coordinate system which can be considered to be “at rest”. And here comes the novelty: this is the case with our e-point structure. El Na- schie’s Zero set, which personifies this structure, provides a coordinate system which is naturally “at rest” in the System of the World!

We can thus point to the possibility of finding a “Xon signature”, not only in the electron spin as we did in [2] , but in the spin carried by all the SM elementary particles―including the photon, assuming it exists in its own right. If the photon exists and carries a spin, it is because it is a Xon in disguise (Figure 5).

Of course, this displaces the mystery: why are the noX and the Xon spinning?

For now, we shall be satisfied to say, well, they are―but not any odd way: they are spinning in the framework of an Absolute space which has a fractal dimension less than 1―an interesting prospect, isn’t it?

14. Conclusions

In a preceding Note [3] , we established connections between Alexandria theoretician Mohamed S. El Na- schie’s E infinity theory and our own Xonic Quantum Physics which places dynamical action, rather than space- time and energy, at the core of the System of the World. In the present Note we sought to uncover new connec- tions between these two theoretical approaches. The endeavor has yielded a surprising result: E infinity contains

a hidden structure dotted with a fractal dimension less than 1 and which possesses characteristics that Isaac Newton attributed in his days to Absolute space, thus providing a coordinate system “at rest” in the System of the World, and in the context of which it becomes possible to understand at long last the origin and nature of the mysterious attribute that all particles listed in the Standard Model of Elementary Particles have in common, an intrinsic angular momentum, the spin.

As we know it today, Quantum Physics is encumbered by many unresolved questions conveniently swept un- der the rug. We addressed one of them in the present Note. We shall reserve for forthcoming publications the consideration of other deeply fundamental questions which perturb the good functioning of Quantum Physics. We shall be satisfied with the spectacular result that we have obtained concerning the nature and the origin of particle spin in concluding this Note.

Acknowledgements

We wish to express our appreciation to Ms. Clara Gao and to Ms. Kelly Sang, JMP Editorial Board Assistants, for their valuable help and advice in properly formatting this paper for publication.

References