Journal of Modern Physics
Vol.06 No.04(2015), Article ID:54710,6 pages
10.4236/jmp.2015.64040
The Relativistic Mechanic Theory of the String
Mohamed Salem
Omar Al-Mukhtar University, Bayda, Libya
Email: m_you_2006@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 February 2015; accepted 13 March 2015; published 17 March 2015
ABSTRACT
In this article, a novel speculative method is used to derive the relativistic mechanic that governs the motion of the vibrating string within the compactified-dimensions spacetime. This mechanic claims that the relativistic mechanic of the special relativity should be only valid for the motion within the familiar four-dimensional spacetime. However, our novel mechanic is valid for the motion within the compactified-dimensions spacetime predicted by the string theory. The equations of this new mechanic show that the vibrating string can move within the compactified dimensions in a speed that is faster than light. It is also shown that this new relativistic mechanic goes to the classical Newtonian mechanic whenever the speed of the vibrating string is much less than the speed of light. Since the proposed mechanic does not prohibit the existence faster than light motion, it may uncover some of the mysteries regarding the string theory, such as the existence of tachyon and time travel. The main goal of this paper is to show that the motion within the compactified- dimensions spacetime obeys a different relativistic mechanic that will provide a startling and revolutionary perspective on the universe and answer some of the fundamental questions posed in the modern physics.
Keywords:
String Theory, Tachyon, Superluminal Motion, Special Relativity, Elementary Particles

1. Introduction
Before 1905, physicists used the Newtonian mechanic to describe the motion of any object without considering any upper limit on the speed. This mechanic was formulated by observing and describing the motion of such objects. This formalism is very successful in describing a wide range of phenomena that occur at low speeds. However, it fails to describe properly the motion of objects whose speeds approach that of light [1] . In 1905, Albert Einstein proposed his relativistic mechanic of the special relativity which showed that a particle needed infinite energy to accelerate to the speed of light. His relativistic mechanic showed that the Newtonian mechanic was only applicable for particles that moved in a speed that was much less than the speed of light, which reduced the Newtonian mechanic as a limiting situation [1] .
Although the special relativity gives a better vision for the universe and spacetime, we still believe that there is a limit for the applicability of this theory. In our point of view, the relativistic mechanic of the special relativity can be applicable to the motion within the familiar four-dimensional spacetime. However, the motion within the compactified-dimensions spacetime predicted by the string theory requires another relativistic mechanic that needs to be discovered. Therefore, a novel speculative method is used to derive this relativistic mechanic. This method is based on the suggestion stated by the American physicist Richard Feynman in 1994. He suggested that a positron could be described mathematically as an electron that was traveling backward in time [2] . We believe that the only explanation for the time travel lies in the compactified-dimensions spacetime predicted by the string theory. We will see in this paper how this dilemma is resolved. By using very convincing speculation, the new mechanic, with its consistency and simplicity, could cause a very dramatic change in our viewpoint of the universe.
2. The Relativistic Mechanic of the Special Relativity
The two famous postulates of the special theory of relativity lead to the following relativistic relationships,
 (1)
(1)
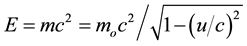 (2)
(2)
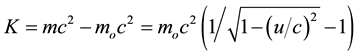 (3)
(3)
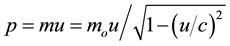 (4)
(4)
where m is the relativistic mass, mo is the rest mass, u is the velocity, c is the speed of light, E is the relativistic energy, K is the relativistic kinetic energy, and p is the relativistic momentum. As it can be easily noticed, these equations give imaginary values whenever u is greater than c [3] .
The special relativity equations can be applied to any particle moving in spacetime with four dimensions without considering the motion of its inner structure (i.e. the motion of its string(s)) that is happening in spacetime with compactified dimensions. For this inner motion of the particle, we will, speculatively, derive different relativistic mechanic that give no imaginary mass for the superluminal motion which might give a new view for the concept of tachyon.
3. The Relativistic Mechanic of the String
3.1. The Relativistic Mass
Experiments have proven the correctness of the special theory of relativity. The equations of this theory can be applied to any accelerated particle that is composed of one vibrating string (e.g. the electron) or more than one vibrating string (e.g. the proton). This means that the motion within the four-dimensional spacetime has an individual effect on every single vibrating string that is moving within the compactified-dimensions spacetime.
Now, in order to derive the relationship between the relativistic mass and the velocity of the vibrating string, we will consider both the electron and its anti-particle, the positron. In 1949, the American physicist Richard Feynman showed that a positron could be described mathematically as an electron that is traveling backward in time [4] -[7] . Since they travel in different directions of time, then one of the vibrating strings should represent a positive relativistic mass and the other should represent a negative relativistic mass. Having relativistic masses with different signs for the strings of the electron and positron means having different velocities within the com- pactified-dimensions spacetime. But, since they are the same particle, then, for the vibrating string motion within the compactified-dimensions spacetime we need a mass-velocity equation that shows a similar dependency in different ranges of speed for both the positive and negative relativistic mass (i.e. symmetric function). The only logic function that satisfies this condition is the following cosine function
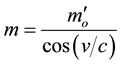 (5)
(5)
where m is the relativistic mass, 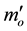 is the rest mass, v is the velocity of the vibrating string, and c is the speed of light. From this equation, which is plotted in Figure 1, we can notice that
is the rest mass, v is the velocity of the vibrating string, and c is the speed of light. From this equation, which is plotted in Figure 1, we can notice that 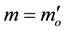 when
when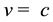 . We can also notice that,
. We can also notice that,
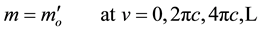

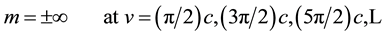
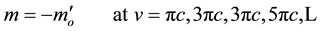
Equation (5) gives the relativistic mass in terms of the rest mass and velocity within the compactified-dimen- sions spacetime. However, Equation (1) gives the relativistic mass in terms of the rest mass and velocity within the four-dimensional spacetime. Equation (5) also shows that the vibrating string can travel faster than light within the compactified-dimensions spacetime. However, as we will see from Equations (7) and (12), this superluminal motion cannot be noticed in the four dimensional spacetime. Figure 1 clearly shows the symmetry between the curves that are above the abscissa (which represent the positive relativistic mass) and the curves that are below the abscissa (which represents the negative relativistic mass). It also shows an infinite number of speed ranges for both the positive and negative relativistic masses.
Assuming in the rest case of the electron (i.e. u = 0 and m = mo), its vibrating string is moving within the compactified dimensions with a velocity of v1, then using Equation (5) we can write,
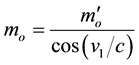 (6)
(6)
Substituting Equations (5) and (6) into (1) we find the relationship between u and v as following,
Figure 1. The change of the relativistic mass with the velocity of vibrating string.

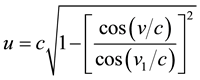 (7)
(7)
Interestingly, if we rewrite Equation (5) in the form
then we expand the function under the square root into a Taylor’s series, it becomes

which clearly appears to be very similar to Equation (1).
3.2. The Relativistic Energy
From Equations (2) and (5), we find that the relativistic energy represented by a vibrating string is,

which shows that the energy still equals mass times the speed of light squared. This equation gives the total relativistic energy in terms of the rest mass and velocity within the compactified-dimensions spacetime. However, Equation (2) gives the total relativistic energy in terms of the rest mass and velocity within the four-dimensional spacetime.
3.3. The Relativistic Kinetic Energy
Consequently, the relativistic kinetic energy will be,
or

If we expand Equation (10) into a Taylor’s series, we obtain,
which goes to the classical Newtonian expression for
3.4. The Relativistic Momentum
If we substitute Equations (5) and (7) into Equation (4), it becomes

This equation represents the relativistic momentum in u-direction (i.e. the four-dimensional spacetime momentum). However, the relativistic momentum for the vibrating string in v-direction (i.e. the compactified-di- mensions spacetime momentum) can be obtained by letting v1 = 0. Therefore, by substituting in Equation (11) we obtain

This equation is plotted in Figure 2. Likewise, if we expand Equation (12) into Taylor’s series, we obtain,
which also goes to the classical Newtonian expression for
Equation (12) can also be obtained by the classical Newtonian mechanic with one modification. From the classical mechanic we have
thus

1This equation shows that whatever the velocity of the vibrating string is within the compactified-dimensions spacetime, it will never exceed the speed of light within the four-dimensional spacetime. In fact, if we expand Equation (14) into a Taylor’s series, then we will notice that both velocities are equal at
Since we are dealing with different type of spacetime, we should replace the velocity u here with the velocity v. How can we do this? In fact, we can just easily use Equation (7) after letting v1 = 0. This will make Equation (7) looks like

Figure 2. The change of the relativistic momentum with the velocity of the vibrating string.
This equation relates the velocity of the vibrating string (v) within the compactified-dimensions spacetime to the total velocity of the vibrating string within the four-dimensional spacetime. Now, by substituting Equations (10) and (14) into (13), we obtain
by performing the integration we obtain
which is Equation (12).
Also, from Equations (9) and (12) we can obtain the following relationship,

Interestingly, the same expression can be obtained by using the mechanic of the special relativity. This expression suggests that a particle may have energy and momentum even if it has no rest mass. Thus when
3.5. The Relativistic Force
By differentiating the momentum Equation (12) with respect to time, we will obtain the force acting on the moving vibrating string

Since the string theory seeks to unify the four fundamental forces in nature, we believe that this equation could carry very important information regarding this unification.
4. Discussions
The novelty of the new speculated relativistic mechanic lies in its correctness, consistency and simplicity. This mechanic goes to the Newtonian mechanic whenever the speed is much less than the speed of light. It also shows that there is an infinite number of velocity ranges. However, every vibrating string is trapped within a certain range of velocity and it cannot escape this range. According to this mechanic, the concept of the imaginary mass is physically unrealistic. Figure 1 shows an infinite number of symmetrical curves for the positive relativistic mass (that is traveling forward in time) and the negative relativistic mass (that is traveling backward in time). This actually might predict the existence of infinite number of the same elementary particle with different vibrating string velocity. If we also look into Figure 1, we can notice that 
According to our theory, the two different spacetimes are directly related to each other. For example, if we consider that the vibrating string of the electron is trapped, for instance, within the first range (0 - (π/2)c), then according to this theory, as we are trying to accelerate this electron within the four-dimensional spacetime to make it reach the speed of light, we actually at the same time are trying to accelerate its vibrating string within the compactified-dimensions spacetime to make it reach the speed of (π/2)c.
To this end, we strongly believe that our proposed mechanic can provide the string theory with a strong evidence of its correctness.
5. Conclusion
This paper suggests that the motion within the compactified-dimensions spacetime predicted by the string theory requires a different relativistic mechanic that is different than that presented by the special theory of relativity. A speculative method is used to derive this relativistic mechanic. It is, accordingly, shown that the vibrating strings of a particle (or any matter) can move faster than light within the compactified-dimensions spacetime. In our point of view, this new mechanic could be the road into more understanding of the laws of nature.
References
- Serway, R.A. and Jewett, J.W. (2014) Physics for Scientists and Engineers with Modern Physics. 9th Edition, Cengage Learning, Boston.
- Young, H.D. and Freedman, R.A. (2003) University Physics with Modern Physics. 11th Edition, Addison Wesley, Boston.
- Kittel, C. (1995) Berekley Physics Course. Vol. I, “Mechanics”. McGraw-Hill College, New York.
- Greene, B. (2010) The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. 2nd Edition, W. W. Norton & Company, New York.
- Ohanian, H.C. (1987) Modern Physics. Int. Edition, Prentice-Hall.
- Blatt, F.J. (1992) Modern Physics. Int. Edition, McGraw-Hill, New York.
- Wichmann, E.H. (1995) Berekley Physics Course, Vol. III, “Quantum Physics”. McGraw-Hill College, New York.
















