Received 29 January 2015; accepted 16 February 2015; published 25 February 2015

ABSTRACT

The gravitational signature of antimatter has received growing interest during the past few decades. Much of the theoretical work in ordinary tensor gravity rules out any difference in the gravitational interaction of matter and antimatter. Fundamental principles and theoretical models describing the nature of matter and antimatter are reviewed. The implication of a probable repulsive field between matter and antimatter and its far reaching consequences on certain cosmic issues, such as the early phase of the Big Bang, the Hawking radiation, virtual particle production and annihilations, are discussed. Experiments designed to probe the gravitational signature of antimatter are reviewed, and a new space-borne experiment to probe the nature of matter-antimatter interactions is proposed.

Keywords:

Antimatter, Gravitation, Interactions

1. Introduction

The discovery of the positron, following the theoretical work of Dirac in 1932 [1] [2] , marked a new era in our understanding of the world of particles. Since then, a whole range of antiparticles has been discovered. The Standard Model (SM) extends the concept of antiparticles to include all known leptons, mesons, hadrons, and force carrier bosons. In the last few decades, the scientific community witnessed a growing interest in acquiring knowledge about the constituents of matter and antimatter and their interactions [3] [4] .

Toward achieving this goal, immense theoretical work has been conducted and large experimental setups have been constructed to identify the theoretical models that best fit the natural world [5] -[8] . In this quest, researchers tried to answer the following question: could there be an antigravity tensor? In other words, does antigravity exist? Despite dedicated efforts, certain fundamental problems in this regard remained unanswered. One of the most basic questions is the gravitational interaction between matter and antimatter. Attempts to build quantum theories of gravity have led to the emergence, in addition to the gravitational force mediated by spin-2 gravitons, of two more forces mediated by spin-0 and spin-1 partners [9] [10] . The CPT (Charge-Parity-Time reversal) theorem is at the origin of the argument describing the gravitational nature of forces arising from the exchange of graviton mediator particles, and it is almost impossible to construct a theory that violates CPT in flat spacetime [11] . However, in curved spacetime, no generalization of the CPT theorem has been unequivocally demonstrated [12] [13] , and the validity of the CPT theorem, in this case, is open to question.

Antigravity arising from matter-antimatter repulsion might have deep implications on current scientific theories. One of the key issues in cosmology is why the universe is composed of matter and not antimatter. A repulsive gravitational force between matter and antimatter could be at the core of a plausible theory that answers this question. Goldhaber [14] has speculated that the universe might have separated into galaxies or clusters of galaxies that are entirely composed of matter and others that are entirely composed of antimatter. Alfvén and Klein [15] and Alfvén [16] addressed this issue by proposing a cosmology based on an electromagnetic plasma separation of matter and antimatter assisted by gravitational forces. Furthermore, a repulsive gravitational force between matter and antimatter could explain certain cosmological observations that escape our understanding based on current theories. In this work, we address these issues in the framework of the available observational data, and we investigate the possible extension of certain astrophysical theories. Today, the absence of observational evidence of antimatter at the large scale is viewed as a problem of the early universe.

Over the past few decades, many experiments have been devised to measure the acceleration of antiparticles in a gravitational field. So far, none of these experiments has been successful in settling the problem of the gravitational signature of antiparticles, albeit a noticeable progress has been achieved [17] . Antihydrogen atoms are currently being used by many research groups [18] [19] in an attempt to reach a definite answer to this issue in the coming few years. In this work, we also propose a new space-borne experiment, which is an extension of the current efforts to determine the response of antiparticles to a gravitational field.

2. The Equivalence Principle of Antiparticles

The equivalence principle is a cornerstone of general relativity and all metric theories of gravity. The weak equivalence principle states that the inertial and gravitational masses are equal. Different versions of the principle have been applied to different classes of phenomena [20] . The weak equivalence principle (WEP) is restricted to mechanical quantities, whereas the Einstein equivalence principle (EQP) exhibits more general aspects that involve WEP and all non-gravitational phenomena. The inertial mass 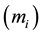and the gravitational mass of a body in the Earth’s gravitational field can be expressed as: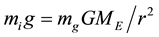, where G is the universal gravitational constant, 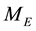is the mass of the Earth, and r is the distance of the body from the center of the Earth. According to Einstein’s formulation of the equivalence principle [21] , an observer in free fall has the right to consider his state as being one of rest and his environment as being gravitationally field-free [22] .

In the 1800s, Eötvös made some geophysical exploration [23] to test the principle of equivalence using a torsion balance. He compared the relative acceleration of pairs of different materials toward the Earth. Eötvös reported null results with an accuracy of 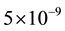[24] [25] . Subsequently, Dicke [26] and Braginsky [27] verified the principle of equivalence by measuring the relative acceleration of objects toward the Sun to accuracies of 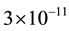and, respectively. Data from laser ranging [28] verified the principle of equivalence for the Moon in comparison to the Earth to an accuracy of 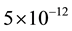[29] . In 1986, Fischbach et al. [30] published their re-analysis of the Eötvös experiment. They correlated the null results of Eötvös with the baryon number per unit mass, and concluded that this evidence was in agreement with the data of Stacey’s group on 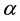and (see Equation (1)). This work created a sensation when the authors further suggested that this was evidence for a vector force due to hypercharge [30] [31] , a “fifth force”. This announcement was at the origin of the great controversy.

3. CP Violation and the CPT Theorem

A parity transformation in quantum physics involves the change in sign of one spatial coordinate, where a parity inversion transforms a chiral phenomenon into its mirror image. All the laws of physics are believed to be exactly the same when looked at in a mirror image of the world. Thus, when watching a physics experiment reflected in a mirror, observers believe that they are seeing reality. This is referred to as parity invariance. Three of the fundamental forces of nature, namely―the electromagnetic, the gravitational, and the strong nuclear forces are found to obey parity invariance. The weak force, on the other hand, was found to be an exception, until it was realized that replacing matter with antimatter, also called charge reversal, will establish charge-parity (CP) invariance. Further investigation revealed an anomaly in the decay of the K-meson [32] , which was a fingerprint of the violation of the CP invariance principle. Subsequently, other mesons were discovered to violate the CP theorem. CP violation can be removed by introducing time reversal (T) to form a coherent CPT theorem that holds for all physics phenomena [33] -[36] . The implication of CPT symmetry can be visualized as a mirror image of our universe with all matter replaced by antimatter (charge inversion or conjugation), all objects having their position reflected by an imaginary plane (parity inversion), and all momenta reversed (time reversal). CPT implies that particles and antiparticles have the same inertial masses and lifetimes, and equal but opposite charges and magnetic moments. Therefore, one of the important aspects to be considered is the ratios of the inertial masses of and of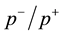. The difference in masses was found to be: at the 90% confidence level [37] , and 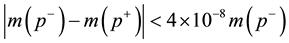to one standard deviation [38] . It was shown that CPT violation implies Lorentz symmetry breaking [39] . The overwhelming majority of the experimental work to look for Lorentz violation yielded negative results [11] [40] . However, one has to remember that CPT invariance is not necessarily deeply rooted in the physical world the way, for instance, the conservation of energy is. In fact, Oksak and Todorov [41] and Stoyonov and Todorov [42] have shown that the CPT theory can be violated when non-finite-dimensional representations of the Lorentz group are allowed. Wald [43] has argued that the CPT theorem may face obstacles when applied in curved spacetime. In reality, many models have been proposed that predict a small CPT violation in curved spacetime [44] -[47] . In the next section, the CPT theorem will be shown to govern our understanding of baryogenesis in the early universe.

4. Baryogensis, Sphalerons, and Cosmic Implications

In this section we briefly discuss the processes leading to the predominance of matter over antimatter. The universe we observe consists almost entirely of matter. Observational evidence reveals that there are no galaxies in the vast regions of the universe consisting of antimatter [48] [49] . Antimatter is produced only locally in processes involving high energies. This observation has its roots in the early stages of the Big Bang. Baryogenesis refers to the hypothetical processes that led to an asymmetry between baryons and antibaryons in the early universe. As outlined in the previous section, the CPT theorem implies that a particle and its corresponding antiparticle have exactly the same mass and lifetime, and that they exhibit exactly opposite charge. In 1967, Andrei Sakharov proposed a set of conditions to explain the predominance of matter over antimatter in the early universe [50] . The first condition requires a violation of the baryon number to produce an excess of baryons over antibaryons. The second condition involves C-symmetry violation so that the interaction produces more baryons than antibaryons without being reciprocally counter balanced by reversal processes. CP violation is also required because otherwise an equal number of left handed and right handed baryons will be produced. The last condition states that the interaction must be out of thermal equilibrium, since otherwise CPT symmetry would lead to compensation between processes involved in increasing or decreasing the baryon number [51] . In the Standard Model, baryogenesis requires the electroweak symmetry breaking to be a first order phase transition; otherwise, sphalerons will remove any baryon asymmetry that is produced up to the phase transition [52] . This argument concerning the CPT theorem is valid in flat spacetime.

A sphaleron is a time independent solution to the electroweak field equations of the Standard Model of particle physics. Sphalerons are responsible for processes leading to the violation of the baryon and lepton numbers. These processes are non-perturbative, and therefore cannot be represented by Feynman diagrams. In the Standard Model, processes violating baryon number convert three baryons to three antileptons, and thus violate the conservation of the baryon number (B) and lepton number (L), but keep the difference B - L conserved. In reality, a sphaleron may convert baryons to antileptons, and consequently a quark may be converted to 2 antiquarks and an antilepton. On the other hand, an antiquark may be converted to 2 quarks and a lepton. Under normal conditions, sphalerons are extremely rare, but they would have been more common at the higher temperature of the early universe. If the density of sphalerons is sufficiently high, they would wipe off any baryon asymmetry. This has far reaching consequences on the sequence of events in the early universe. First, any net excess of baryons existing before the electroweak symmetry breaking is wiped off, because sphalerons were abundant at the high temperatures in the early universe. Second, a net baryon excess can be created during electroweak symmetry breaking and be preserved only if the phase transition was first order [51] . In fact, for second-order phase transitions, sphalerons would wipe off any baryon asymmetry as it is created, whereas in a first-order phase transition, sphalerons would wipe off baryon asymmetry only in the unbroken phase [52] . Thus, in baryogenesis, an imbalance of the number of leptons and antileptons is formed first by leptogenesis, and sphaleron transitions then convert this into an imbalance in the number of baryons and antibaryons [51] [53] .

5. Quantum Gravity Force Mediating Particles

In quantum gravity theories, the gravitational force is mediated by the graviton which is a tensor spin-2 particle. In these theories, the spin-2 graviton has spin-0 (graviscalar) and spin-1 (graviphoton) partners [9] [10] . If the masses associated with these new partners are sufficiently small, the force they generate will have enough range to produce measurable effects in the macroscopic world. In field theories, a gaviscalar couples to the trace of the energy-momentum tensor, with the result that the exchange of even-spin bosons, such as the spin-2 graviton, or its spin-0 partner, will always produce attractive forces, whereas the force produced by the exchange of odd-spin particles, such as the spin-1 partner, will produce repulsive forces between like charges and attractive forces between opposite charges [9] . Scherk [54] has emphasized the importance of the vector partner (graviphoton), and has pointed out that it couples only to the CPT-non-self-conjugate degrees of freedom, but not to gauge bosons such as the photon. Goldman et al. [55] noted that these partners of the graviton are necessary for supersymmetry, which is at the core of certain desirable features such as the cancelation of divergences in theories of supergravity [56] . From a phenomenological point of view, the static potential energy between particles and antiparticles is given by [57]

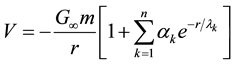(1)

where the range 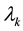of the component of the non-Newtonian force is linked to the mass of the mediating antiparticle through the relation

. (2)

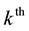
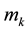
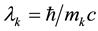
Here, , where is the Planck constant, and c is the speed of light. in Equation (1) is the coupling constant. Equation (1) predicts more than one spin-0 and spin-1 particles. For convenience, we restrict the gravitational potential to the exchange of one spin-0 and one spin-1 particles only. In this case, Equation (1) becomes [58]

(3)

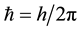
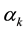
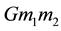
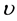
where a and b are the moduli of the product of the vector and scalar charges in units of, and and s are the inverse graviphoton and graviscalar masses (ranges). The ± sign applies to the matter-antimatter interaction. In general, these charges are some linear combination of baryon and lepton numbers, and the force will therefore be composition dependent [59] . The graviphoton and graviscalar are likely to have small masses [60] (large and s). Macrae and Riegert argued that zero masses are not to be ruled out [61] .

The Newtonian limit of gravity has only been tested to a high accuracy at laboratory distance scales, and in the solar system at distances of 10⁶ to 10¹³ m. At intermediate distances, deviation from the inverse square law has not been excluded [62] . Stacey and coworkers [63] [64] identified certain anomalies when conducting geophysical experiments which are consistent with deviations from Newtonian gravity on length scales between 1 and 10⁶ m. They analyzed their data using only one Yukawa term of the gravitation interaction energy between two massive fermionic objects, separated by a distance r,

. (4)

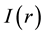
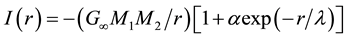
They found an effective repulsive parameter with [63] ,

(5)

Equation (5) involves large uncertainties. Nevertheless, an observation of a definite repulsive component is claimed.

Antiproton experiments were originally proposed to investigate the possibility that antimatter could have a different gravitational acceleration than matter [65] [66] . In 1985, Zacho [67] observed that a vector partner would produce an attraction for antiprotons, and would cancel normal gravity for matter if the vector had zero mass. Goldman et al. [59] noted that the gravitational potential given by Equation (3) would have a very small effect in matter-antimatter interactions. This happens when and. This situation indicates an approximate symmetry between the two partners. If a difference is to arise from symmetry breaking, or higher-order gravitational corrections, then and become truly negligible [68] . This demonstrates the need to conduct antimatter-matter experiments. In the past few decades, it was realized that theoretical work on matter-antimatter has to be subjected to accurate experimental tests by taking advantage of the latest technology.

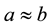
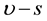
6. Arguments against Antimatter

Antigravity stimulated considerable research work in the past few decades. The concept of antigravity can be traced back to the classical work of Maxwell in the unification of electricity and magnetism [69] [70] . Maxwell noticed that both electromagnetism and gravitation obey an inverse square law, but they are different in that for electromagnetism, opposite charges attract and like charges repel, whereas for gravitation the bodies concerned are all of the same kind, and a gravitational force is always attractive. This observation led Maxwell to conclude: “The intrinsic energy of the field of gravitation must therefore be less wherever there is a resultant gravitational force. But as energy is essentially positive, it is impossible for any part of space to have negative energy. Thus, Maxwell refuted the idea of antigravity on the basis of the violation of the law of conservation of energy. In the modern era, our knowledge about the world is shaped by the revolutionary theories of quantum mechanics and general relativity. Thus, the gravitational attraction is mediated by a tensor spin-2 particle (graviton) with the charge being the mass-energy [71] . For electromagnetism, on the other hand, there exist both positive and negative charges, and the force in this case is mediated by a vector spin-1 field that produces a repulsive force between like charges and an attractive force between opposite charges. Physicists are thus led to search for a general law that governs the signature of the force mediated by tensor and vector fields [72] [73] . In the modern era, three other classical arguments against antigravity emerged. However, it turns out that none of these arguments can withstand modern ideas stimulated by quantum gravity.

6.1. The Morrison Argument

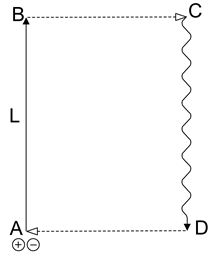
The first of these arguments is due to Morrison [74] , in which he considered the energy conservation of a matter-antimatter pair created at the Earth’s surface. The pair is raised adiabatically to a height L with no loss of energy, as depicted in Figure 1. The pair’s annihilation would produce a blue-shifted photonic energy in going back to the Earth’s surface. When energy was converted into the pair, the pair would have acquired a kinetic

energy, and thus energy conservation is violated. Nieto and Goldman [68] discussed Morrison’s argument in terms of the invariance principle and tensor gravity. They pointed out that Lorentz-invariance and quantum theory imply a conservation of energy, no matter what kind of coupling the spin-1 and spin-0 partners may or may not have. It is the total energy and not the energy of the individual particles or even the energy of both particles that is conserved. The above authors have also demonstrated the invalidity of the Morrison’s argument by considering graviscalar and gravivector coupling. Hildebrand et al. [75] , Hughes et al. [76] , and Hughes [77] considered graviscalar fields that are coupled directly to electromagnetism via the square of the field-strength tensor, and have shown once again that these are consistent field theories, resulting in the conservation of energy.

6.2. The Schiff Argument

The second argument against antigravity was presented by Schiff [78] [79] shortly thereafter. Schiff’s argument has been described as ruling out any anomalous gravitational behavior of antimatter [80] [81] . He considered antigravity from the standpoint of the principle of equivalence and quantum field theory, and came to the conclusion that antigravity does not conserve energy. Schiff focused on the probability of finding an antiparticle in a nominally particle state, arising from one-loop fluctuations due to electrodynamics. This probability is then multiplied by the mass of the positron to obtain a scale of the antigravity interaction energy with the Earth’s potential. He then compared the “net” quantity of atoms of different atomic number, Z, with the constraint of the Eötvös experiment [24] . Thus, Schiff considered quantum field-theoretic corrections to a quantum field theory of gravity coupled to matter. However, quantum general relativity coupled to matter is not renormalizable at even the one-loop level. Nieto and Goldman [68] deeply criticized the normalization technique, and found that his calculation is entirely moot in modern theories of quantum gravity.

6.3. The Good Argument

The third argument was proposed by Myron L. Good [82] in 1961. Good argued that antigravity would lead to an unacceptable level of CP violation in the anomalous regeneration of kaons. In fact, he observed that if there was antigravity, then the K_L, which is a linear combination of the K⁰ and K⁰, would regenerate into the K_S’s. The energy difference between K⁰ and K⁰ due to antigravity should be [68] , where is the gravitational potential that he assumed to have absolute meaning. Since K_L is a linear superposition of the K⁰ and K⁰, the K_L’s in the beam should instantaneously start regenerating some K’s, because the relative time variation of the K⁰ and K⁰ components is [68] . Since the K_L’s did not regenerate K_S’s (as stated earlier when discussing the CP violation), Good came to the conclusion that the antigravity statement is excluded. Nieto and Goldman [68] criticized the Good argument by noting that in modern gauge theories the potential difference is the important quantity, and there is no meaning to an absolute potential for an infinite range force. To sum up this section, all three arguments against antigravity are refuted on the basis of theories of quantum gravity and gauge theory.

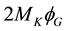
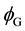
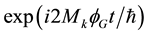
7. Theories Predicting Antigravity

Several theories that predict antigravity have been advanced during the last decade. Most of these theories are purely mathematical with no obvious way of testing them experimentally. In what follows, we highlight some of these theories and outline their main principles and predictions.

7.1. Classical Isodual Theory of Antimatter

The first mathematical theory predicting the repulsion of antimatter by the gravitational field was introduced by Santilli [83] in 1994. In this work, Santilli showed that the isodual theory predicts that antimatter in the field of matter experiences antigravity. He noted that there is an imbalance in the physics of matter, which is prevalent at all levels of study from Newtonian mechanics to quantum field theory, and antimatter which is solely treated at the level of second quantization [84] . Santilli advanced the hypothesis that “Antimatter is characterized by isodual mathematics, and with dual numbers, fields, spaces, etc., thus having negative-definite units and norms. Therefore, all characteristics of matter change sign for antimatter in the context of isoduality” [84] . In general relativity, antimatter representation in isodual Riemannian geometry has a negative-definite energy-momentum tensor. According to the above hypothesis, the trajectories we observe for antiparticles are the projection in our spacetime of the actual trajectories in isodual space. This principle, when applied to the case of the gravitational field, yields antigravity. Santilli concluded that “the classical representation of antiparticles via isoduality renders gravitational interactions equivalent to the electromagnetic ones, in the sense that the Newtonian gravitational law becomes equivalent to the Coulomb law.”He also conjectured that the various arguments against antigravity, such as those introduced by Morrison [74] , Schiff [78] [79] , Good [82] , and others don’t apply under isodualities, owing to their essential dependence on positive units [84] .

7.2. Elementary Process Theory

Cabbolet published in 2010 the first non-classical principles governing matter-antimatter gravitational repulsion [85] [86] . This approach was formulated in what he called Elementary Process Theory (EPT). This theory is a formal axiomatic system with potential application as a foundational framework for physics, supporting the idea of gravitational repulsion between matter and antimatter. The core of the theory is to identify the laws of physics that would govern the universe if antimatter, with a rest mass, is repelled by the Earth’s gravitational field. The theory involves formalizing seven non-logical axioms of the system, with interpretation rules for the terms of the language with the intention that every theorem of the system yields a true statement about physical reality. The author found an incompatibility between quantum mechanics and general relativity with the EPT. To demonstrate the applicability to real world problems to which neither quantum mechanics nor general relativity applies, the principles of the EPT have been applied to understand what might have happened during the Planck era of the Universe, and to show how gravitational repulsion (if it exists) might function [85] . Nonzero rest mass particles such as electrons, protons, neutrons and their antimatter counterparts are characterized by a stepwise motion as they change their states from particle-like to wave-like. Gravitation then occurs when the particle is in the wave-like state, which allows, for example, the wave-like state of the electron and positron to interact differently with the Earth’s gravitational field.

7.3. Villata’s Theory

Villata argued that antigravity appears as a prediction of general relativity when CPT theory is applied [87] . Villata constructed a new equation by applying discrete operators for charge (C), parity (P), and time reversal (T) to the equation of motion of general relativity for a particle in a gravitational field. The resulting equation becomes (Equation (8) in Villata 2011, Ref. [87] )

(6)

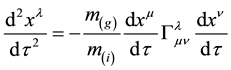
The new constructed equation becomes (Equation (9) in Villata 2011, Ref. [87] )

(7)

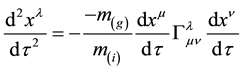
This equation is then interpreted as describing the behavior of antimatter in the gravitational field of ordinary matter, and it predicts a repulsion of matter and antimatter. Cabbolet [88] criticized the approach of Villata on the ground that quantum physics from which the CPT symmetry is taken and relativity theory are two distinct paradigms in physics that are proven to be incompatible. Therefore, it is at least an epistemologically controversial practice to add a theorem of one paradigm as an additional assumption to the other [88] . Cabbolet argued that the method employed by Villata for the theory’s construction is in itself inadmissible, and that the resulting equation cannot be reconciled with the ontological prepositions of general relativity.

Villata [89] responded to the above comment by noting that the criticisms are of a methodological and an ontological kind that arise from a misinterpretation of some concepts, perhaps due to some lack of clarity or some omissions of details in his original article. Villata provided additional explanations regarding the assumptions and results of the theory.

8. Particle and Antiparticle Gravity Experiments

Fairbank and Witteborn set up an experiment to compare the gravitational acceleration of electrons and positrons by analyzing the time of flight distributions of electrons falling freely inside a vertical metal drift tube [90] . The tube was designed such that the stray electric field and magnetic field gradients are reduced to less than 10⁻¹¹ V/m. However, the Schiff and Barnell effect [91] caused electrons inside the metal of the drift tube to sag under gravity, until the gravitational force was balanced by the electrostatic force of compression. This created an electric field inside the drift tube. Other phenomena, such as the patch effect, may also produce stray fields in the tube. It is caused by fields arising from irregularities in the surface of the crystalline structure of a conductor. Subsequent investigations concerning the possibility of conducting experiments using antiprotons also faced the same problem of stray fields. Brando et al. [92] were interested in conducting experiments using antineutron beam time-of-flight techniques. However, it has not yet been possible to obtain both low-energy and well-defined beams of antineutrons; they are produced at high energy and any attempt to cool them down or diffract them may lead to their annihilation [92] .

9. Antihydrogen Experiments

The production of antihydrogen was proposed to overcome the above difficulties. After the successful production of antihydrogen, many research groups tried to find a way to cool them using laser techniques and to store them in a magnetic trap. This way, measurements of gravity could be performed on antihydrogen atoms, which would circumvent the sensitivity to stray electric fields [93] . Antihydrogen atoms were first brought into existence in CERN in 1995. The experiment was performed using the Low Energy Antiprotons Ring (LEAR). Fermilab soon confirmed the CERN results by producing approximately 100 antihydrogen atoms. It turns out that these antihydrogen atoms are too “hot” to be used for gravitational studies. In the late 1990s, two collaborations were formed, namely, ATHENA and ATRAP. The ATHENA collaboration disbanded in 2005, and a new collaboration named ALPHA was formed. The antiprotons used in these experiments are first cooled by decelerating them with the Antiproton Decelerator (AD), and then passing them in a foil, before capturing them in a Pinning-Malmberg trap [94] . The overall cooling process was highly inefficient with only 0.1% of the antiprotons leaving the Antiproton Decelerators finding their way to the Pinning-Malmberg trap. When trapped, the antiprotons are initially cooled bya plasma of electrons via cyclotron radiation. This is achieved by Coulomb collisions with antiprotons. The electrons are then removed by the application of short duration electric fields. Thus, the antiprotons will eventually have their energy lowered. A second trap, placed next to the Pinning-Malmberg trap, captures a small cloud of positrons. These positrons are produced by radioactive sodium in a Surko-style accumulator [95] . An antiproton-positron plasma is then formed by the manipulation of the trap electrodes. Antiprotons can then combine with positrons to form antihydrogen. Within microseconds, the antihydrogen atoms that have been formed, hit the trap walls and annihilate. However, physical processes may play a role in trapping the antihydrogen atoms for a relatively long time. Antihydrogen atoms are electrically neutral, but they exhibit a magnetic moment produced by the spin of their component particles. A magnetic minimum is formed by the interaction of the resultant magnetic moment with an inhomogeneous magnetic field. The antihydrogen atoms are then attracted to the magnetic minimum. Antihelium-3 nuclei were first produced in the 1970s in proton-nucleus collision experiments [96] . Subsequently, they have been produced by the collision of lead nuclei [97] . In 2011, the STAR detector announced the observation of antihelium-4 nuclei [98] . However, the production of antihelium atoms for use in gravitational acceleration measurements remains an area for future investigation.

The ALPHA collaboration announced in 2010 the trapping of 38 antihydrogen atoms for 0.167 of a second [99] , and in April 2011 they announced the trapping of 309 antihydrogen atoms for about 1000 seconds [100] .

The AEGIS experiment was originally proposed in 2007. Its aim is to carry out the first direct measurement of the gravitational acceleration of antihydrogen atoms by sending a stream of these antiparticles through a series of diffraction gratings, the pattern of light and dark patterns would ideally enable the position of the beam to be pinpointed with up to 1% accuracy. Their plan is to produce ultracold antihydrogen atoms via collisions of ultracold (mK) antiprotons with Rydberg positronium. Construction of the main apparatus was completed at the end of 2012; investigations with electrons and positrons have been going on since then. Between December 2012 and August 2014, no antiprotons were available at CERN, since all accelerators were being refurbished, but since August 2014, antiprotons are once again available.

The GBAR collaboration proposes the production of ultracoldantihydrogen atoms after the cooling down of antihydrogen ions to about 100 µK [101] . The precision on the measurement of the gravitational acceleration of antihydrogen atoms is statistically limited and depends upon the temperature of the antihydrogen ions. The experimental technique used by the GBAR collaboration follows the original idea of Walz and Hänsch [102] , where the ions are first produced and are then cooled down to few tens of µK by “sympathetic” cooling with cold beryllium ions. The excess electrons can then be removed by a laser pulse to produce antihydrogen atoms.

The theory and applications of antihydrogen has evolved enormously during the past decade, and it has become one of the hot topics in physics research today. It is not the intention of this work to investigate the realm of antihydrogen physics. Interested readers are referred to Refs. [68] [100] [101] .

10. A Proposed Space-Borne Experiment

The time of flight experiments in terrestrial laboratories is relatively short, and stray electric fields can not be avoided unless highly restricted measures are taken. Antihydrogen atoms, proposed by many groups in the past two decades are a promising approach towards settling the uncertainty concerning the gravitational signature of antiparticles. The various collaborations have succeeded over the years in developing robust techniques to produce antiparticles, to cool them, and to form antihydrogen atoms that can be trapped in a magnetic field for a certain period of time. Removal of the magnetic field causes antihydrogen atoms to hit the walls of the container, and thus the time of flight can be recorded. The experimental accuracy of such a system can be highly improved if conducted in a weak gravitational field. One possible approach is to consider a space-borne experiment on the far side of the lunar surface. The first proposal to conduct such an experiment in the lunar environment was advanced by one of the authors in 1998 [103] .

Using current technologies, magnetic traps can be sent to the Moon and released once the experimental setups are ready. However, current technologies are unable to store antihydrogen atoms for more than about 20 minutes, which is far less than the time required to carry the traps to the Moon. Another approach is to create antihydrogen atoms in the lunar environment. The transfer of terrestrial technologies to the lunar environment is a hard task to achieve. Therefore, new technologies, more suited to that environment, need to be developed. One possibility is to trap cosmic antiprotons and positrons to form antihydrogen atoms, since antiprotons are produced in the solar environment [104] , and those that arriveonthe Earth have a characteristic maximum energy of 2 GeV [105] .

The Alpha Magnetic Spectrometer on board the International Space Station detected positrons with energies from 10 - 250 GeV [106] . In July 2012, it was reported that AMS-02 had observed over 18 billion cosmic rays [107] . In February 2013, it was acknowledged that in its first 18 months of operation, AMS had recorded 25 billion particle events including nearly eight billion fast-moving electrons and positrons [108] . Therefore, antiprotons and positrons are present in acceptable quantities to form antihydrogen atoms in space, and thus conducting experiments to measure the gravitational acceleration of antimatter in the lunar environment is highly justified.

11. Matter-Antimatter Interactions: A Cosmic Perspective

Antimatter is produced locally in the universe. One important source of their creation is the appearance of virtual particles where, according to the uncertainty principle, they come into existence for a brief period of time corresponding to their energy. This phenomenon becomes important in the vicinity of the event horizon of black holes. The creation of a particle-antiparticle pair in this region may cause one of the particles to be attracted to the black hole, and thus disappears from our observable universe. The second particle has a probability to remain solitary and may contribute to what is called Hawking radiation [109] . Thus, the quantum vacuum is a source of gravitational mass that depends on the gravitational properties of antimatter. A new idea suggested by Hajdukovic [110] states that the gravitational properties of antimatter determine the properties of the quantum vacuum. The above author conjectured that if antihydrogen falls up, then supermassive black holes should be emitters of antineutrinos.

In 2008, the INTEGRAL satellite discovered a giant cloud of antimatter at the center of the Milky Way Galaxy. The cloud itself is about 10,000 light years across. Several explanations were advanced to explain the origin of the antimatter cloud. It was discovered that X-ray binary star systems are distributed in the same manner. However, it remains a mystery how these X-ray binaries are producing this huge amount of antimatter.

Possible alternative sources include supernovae where, for instance, the radioactive ²⁶Al isotope, produced in some of these supernovae, decays through positron emission and releases amagnesium atom: ²⁶Al → ²⁶Mg^∗ + e⁺. If matter and antimatter have different gravitational signatures, then one may speculate that the creation of say an electron-positron pair in the vicinity of the event horizon of the black hole at the centre of our Galaxy could be the cause of this antimatter halo, since the electrons (matter) will be attracted toward the black hole, whereas the positrons will feel a repulsive gravitational field and form the observed halo.

12. Conclusion

The past two decades have witnessed a revived interest in the gravitational physics of antimatter. A thorough understanding of the gravitational signature of matter-antimatter interactions is essential. Many theories have been proposed to address this issue. Several experiments have also succeeded in shedding some light on this issue. However, the behavior of antimatter in a gravitational field remains, to a certain extent, elusive. Space-borne experiments, including investigations on the Moon’s surface, might pave the way to a better understanding of this fundamental issue.

References