Received 22 January 2015; accepted 6 February 2015; published 10 February 2015

ABSTRACT

Fermion mass is modeled as an analogue of Weyl curvature, which by hypothesis emerges when closed, spin-2 strings sweep out closed world tubes. Second order curvature classes result when closed world tubes circulate and themselves sweep out closed tubes etc. Gauge invariance distinguishes admissible curvature classes from the larger set that would constitute an infinite continuum of possibilities. Admissible curvature classes account for known quark masses and predict a new quark of mass 30 GeV/c². Super-symmetric interactions among prescribed fermions and super-partners conserve electrical charge, I₃, color and generation and are therefore regarded by hypothesis as preserving a minimal irreducible representation of a super-symmetric SU(5).

Keywords:

String Theory, Conformal Field Theory, Quarks, Super-Gravity

1. Introduction

The theory of H. Weyl associates increments of vector magnitude with curvature states

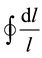(1)

and gauge transformations:

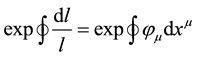(2)

[1] . The model that is proposed here replaces the parallel transport of vectors around closed curves with displacements of closed, spin-2 strings which occur when those strings sweep out closed world tubes:

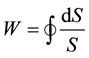(3)

This analogue of Weyl curvature will be known as W-curvature and will be regarded as physically admissible (as time and position independent) if and only if the implicit gauge is preserved in the sense introduced by F. London:

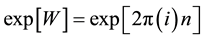(4)

[2] . The proposed model also considers the compounded world tube that occurs when the outer circumference of a world tube (3) sweeps out a closed tube:

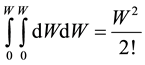(5)

This second order W-curvature is physically admissible if and only if

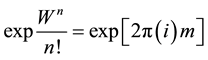(6)

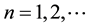;. A generalization of the model that is introduced above clearly generates a state that consists of a higher order curvature:

(7)

, and again the generalized curvature state (7) is, by hypothesis, physically admissible if and only if the implicit gauge is preserved:

(8)

;

By hypothesis the proposed model associates the W-curvature classes (7) with the masses of composite states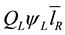, where 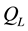is a generic, left-handed quark, 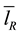is a generic right-handed anti-lepton and is a left- handed field of spin-2 [3] . This hypothesis parallels Wheeler’s ideal which attributes mass to space-time curvature [4] . The composite states are also realizations of the super-unified fields that were proposed by this author in 2004 [5] .

The proposed model is calibrated by associating a specific W-curvature state with the heaviest lepto-

quark state in which the observed quark and lepton share a common generation and where the values of the anti-particles and are characterized by opposite values. Specifically it is postulated

that,

(9)

[6] . In this context, one can model the additional lepto-quark composites in terms of the proposed theoretical structure provided that (9) is consecutively divided by 6, 5, 4, 3 and 2. These divisions produce the following values of W-curvature and mass:

(10)

(11)

(12)

(13)

(14)

Interpretation of the mass (10) will be deferred until the massive states described by expressions (11) through (14) have been interpreted. The theoretical mass represented by (11) motivates the association of (11) with the spin- composite or where is the left-handed bottom quark, where is a right handed anti-bottom quark (an established mass of about 4.3 GeV/c²), where and respectively represent the left-handed tauon and the right-handed anti-tauon (an established mass of about 1.7 GeV/c²) and where, again, represents a left-handed field of spin-.

The theoretical masses that are described by expressions (12) through (14) are also established by observation [6] . They are the masses of the charmed quark, the strange quark and a quark that is designated. The “average quark” is obtained if the masses of the up quark and down quark are averaged and if the values of the up quark and down quark are averaged [3] . With the exception of the spin-2 composite the masses of the leptons and anti-leptons are negligible, so that the masses of those composites associate strictly with the masses of the corresponding quarks.

To interpret the mass of the composite that is described by expression (10), it is first observed that the left- handed muon is not included in the foregoing discussion. In this context the mass that is described by (10) is interpreted as that of the spin- composite. Accordingly the is interpreted as an unobserved, moderately heavy, left-handed quark that is characterized by. Since the mass of the anti-lepton is relatively negligible, the mass of the newly predicted quark will be designated as approximately 30 GeV/c².

2. Pure SUGRA Interactions

Generation and electrical charge are preserved by the pure SUGRA interactions that are described by vertices

(15a)

and

(15b)

Moreover, is implicitly preserved because the interacting states are neutral.

Composites such as and are regarded as realizations of the spin- super-partners of the spin- entities. Additional super-gravitational interactions are represented by vertices

(16a)

and

(16b)

If the generic in the triplets represent the same quark, then an additional quantum number is required to avoid conflict with Fermi-Dirac statistics. Respecting tradition this quantum number is identified with “color”. In this context the spin-(3/2) composites are identified as composites.

It should be observed that identical leptons as well as identical quarks can emerge within composite, spin- super-partners and that such leptons must associate with an additional quantum number (paralleling that which is associated with identical quarks) to avoid conflict with Fermi-Dirac statistics. The already familiar quantum number which is designated “generation” can serve in this capacity.

It is observed that the interaction (16) conserves four quantum numbers: electrical charge, , color and generation. Thus it is postulated that the interaction (16) preserves an SU(5) symmetry. It is also noted that a minimal irreducible representation of SUSY SU(5) can be precisely constituted by the chiral modes that associate with the implied lepton generations and their scalar super-partners. The strictly leptonic representation of the anti-symmetric 10 = [5,2] of SUSY SU(5) can be given by

(17)

where and represent the scalar super-partners of and and where and represent the scalar super-partners of the neutrinos. The strictly leptonic representation of the symmetric 5 = [5,1], complementing can be given by

(18)

where is the super-partner of and is the super-partner of the muon’s neutrino. (Note that and correspond to the same scalar super-partner.) The realization in terms of possible quark classes of the anti-symmetric 10 = [5,2] can be given by

(19)

where “7” designates the predicted quark and “” designates the scalar super-partner of “7”. The realization in terms of quarks of the symmetric 5 = [1,5] can be given by

(20)

where A is the “average quark” introduced above. (The average “A” is obtained by averaging the masses, values and electrical charges of the up quark and down quark. The mass of “A” is about 0.25 GeV/c² and the value of the “A” is zero.) By hypothesis, the energy level at which the composite “A” behaves as an individual quark does not contain super-partners of individual fermions.

The proposed symmetry models an energy interval between the Planck energy (10¹⁹ GeV) and the energy level of grand unification (10¹⁵ GeV) and as such models a marginal domain in which interactions may involve the composites “A” or may involve up-down pairs. By hypothesis, “A” and the up-down pair are never active at the same energy level (never involved in interactions at the same energy level). If “A” is active, then up-down is inactive and conversely. In this context Equation (19) and Equation (20) together model quarks in the entire marginal domain between the Planck level and the grand unification level.

3. Conclusions

Fermion mass is attributed to an analogue of Weyl curvature which, by hypothesis, occurs when closed, spin-2 strings sweep out closed world tubes. Additional classes of massive fermions are attributed to higher orders of curvature that occur as world tubes circulate and, they themselves sweep out closed tubes etc. The proposed hypothesis clearly parallels Wheeler’s ideal, which attributes mass to space-time curvature. The composites which are, by hypothesis, equivalent to W-curvature classes can also be regarded as realizations of the super-unified field that was proposed earlier by this author (a field of spin- and of specific generation, which carries color, is of electrical charge 2/3 and is I₃ neutral). Leptons are converted into quarks by absorptions of such fields. Inverse fields are also postulated.

As an analogue of the Weyl theory, the proposed model is subject to gauge transformations and a requirement of gauge invariance distinguishes admissible curvature classes and consequent mass classes from the larger set that will constitute an infinite continuum of possibilities. The proposed model correctly approximates the masses of observed quarks and of the tauon and predicts a new quark of (approximate) mass 30 GeV/c².

Super-symmetric interactions that conserve electrical charge, I₃, color and generation are regarded as preserving a minimal irreducible representation of a super-symmetric SU(5).

References