Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53221,5 pages
10.4236/jmp.2015.61003
Equivalence Transformations among Ising Models
Yougang Feng
Guizhou University, Guiyang, China
Email: ygfeng45@aliyun.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 November 2014; accepted 18 November 2014; published 14 January 2015
ABSTRACT
Using topology, fractal analysis and investigation of lattice formation process we find two types of equivalence transformations among Ising models: topological equivalence transformation and formation equivalence transformation. With the help of the transformations and the known data of the critical points of simple cubic (sc) lattice and planar square (sq) lattice we get directly the critical points for face-centered cubic (fcc) lattice, body-centered cubic (bcc) lattice and diamond (d) lattice. The transformation itself results no error in the calculation. Other than Monte Carlo method and series expansion approach the equivalence transformations help us simplify much more greatly the calculation of the critical points for the three-dimensional models and understand much more deeply the structural connection among Ising models.
Keywords:
Ising, Critical Point, Fractal, Equivalence Transformation

1. Introduction
Fractal structure is a class of complex ordered structures in nature, which exhibits not simply a higher degree but an altogether different level of complexity. During the 1980s physicists tried to describe phenomena on fractal, they succeeded in calculating some of physical characteristics of fractals [1] [2] . A deterministic fractal is cre- ated by applying a rule of some sort interactively and indefinitely. A fractal is a self-similar geometric structure that looks alike on all length scales. The sub-block and the block in the Ising models are just such type of structures [3] . Our approach combining the fractal analysis and the solvable Gaussian model has been succeeded in calculating the critical points for two-and-three-dimensional Ising models and analyzing the fluctuation structure of the details at the critical temperature [3] - [5] . The explicit investigation of the information about these structures helps us think further that the macroscopic property of an Ising model at the critical temperature is an overall behavior of the collective motion of spins being in excitation state. According to solid state physics the excitation states consist of a series of elementary exciting units having definite energy quanta and relevant quasi-momenta, and have the quantum characteristics. We call these elementary excitations spin phonons [4] [5] . It is the behavior of spin phonons that determines thermodynamic properties of an Ising model at the critical temperature. In the reference [3] two three-dimensional models are facilitated by our theory. The research indicates that an exact solving of a lattice system depends strongly on the accurate analysis on its fractal structure. It is not necessary, then, to analyze the fractals for each lattice system if some equivalence relations among Ising models can be found that transfer some unknown fractal structure into those we have solved successfully.
Mentioning the equivalence transformation we may trace back to the 1940s, Kramers and Wannier discovered a transformation to enable them to get the critical point for square lattice [6] . Onsager pointed out their work to be topologic self-duality transformation [7] . He further discovered a star-triangle transformation, where a star consists of a central spin interacting three neighbor spins and can be transformed into a triangle of three spins interacting each other. The so called “decoration” or “iteration” transformation was discussed by Fisher [8] , leading to solutions for further plane Ising nets and also for lattices in which the spins on alternate sites have a magnitude greater than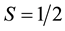 . However, all of three-dimensional lattice systems cannot be solved by his approach, although he found theoretically that there are some transformations between these systems such as a simple cubic lattice and a tetrahedron lattice, with which we are good familiar.
. However, all of three-dimensional lattice systems cannot be solved by his approach, although he found theoretically that there are some transformations between these systems such as a simple cubic lattice and a tetrahedron lattice, with which we are good familiar.
Solving of three-dimensional Ising models has more far-reaching significance because the actual ferromagnetic elements have different crystal textures; for example iron is body-centered cubic (bcc) while nickel is face- centered cubic (fcc). The investigation of their structures will help us deeply understand general laws of ferromagnetic. According to our investigation in the 3-dimensional models there is a unique irreducible lattice: the tetrahedron lattice [3] ; others are reducible and should be divided into sub-blocks. There are two ways to research further: The first is to find out the fractal for the individual lattices one by one, except the sc we have solved, which requires us to divide correctly their sub-blocks; this may not be a normal way of affairs, especially for those composite lattices such as the d lattice. Another way is to look for equivalence relations among the models, using which the fcc, bcc and d models can be described by the sc or the other such as the sq we have solved exactly.
In this paper we find two types of equivalence transformations: topological equivalence transformation and formation equivalence transformation, by means of which we get directly the critical points for the fcc, bcc and d lattice systems. In Section 2, we first introduce some new concepts then derive the two types of equivalence transformations. In Section 3, the two transformations are tested and verified and we further compare different theories of studying Ising models making use of the obtained data. The critical exponents are discussed simply. Section 4 is conclusion remark.
2. Theory
2.1. J and J*
In order to designate the relationship between the structure of a particular model and its critical temperature, and to compare the critical points for different models, it is convenient to unify their coupling constants, the applying of the normalized coupling constant is a wisdom choice. In terms of quantum mechanics the coupling constant is the exchange energy [9] , it can be expressed in the form
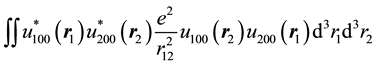 (1)
(1)
The  and
and  are the conjugate states of the wavefunctions
are the conjugate states of the wavefunctions 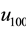 and
and 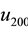 which are the ground states of the first electron and the second electron, respectively, the
which are the ground states of the first electron and the second electron, respectively, the 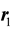 and
and 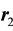 are the electrons position vectors,
are the electrons position vectors, 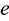 is the electron charge,
is the electron charge, 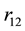 the distance between the electrons. Clearly, the integral is independent of lattice structure. If the
the distance between the electrons. Clearly, the integral is independent of lattice structure. If the 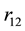 equals one unit length, Equation (1) is the expression of the normalized coupling constant
equals one unit length, Equation (1) is the expression of the normalized coupling constant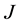 ; while
; while 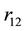 is smaller than one unit length, the integral is just the actual coupling constant
is smaller than one unit length, the integral is just the actual coupling constant . From Equation (1), the relation between
. From Equation (1), the relation between 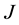 and
and 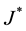 is
is

2.2. 
A normalized critical point is defined as




For the fcc, 

For the bcc, 

For the sc, 

It can be seen that different coupling constants provide different critical points for the same configuration, which critical temperature is unique. The normalized critical point for the sc lattice is just its equivalent critical point.
2.3. Topological Equivalence
The fcc lattice is a familiar structure for us, its structural diagram is often shown in the books on solid state physics. If we consider merely the nearest neighbor interaction the lattice can be considered a structure made up of infinite parallelepipeds, each of which is a primitive cell for the fcc. According to topology such structure is equivalence to the sc, we may call the fcc an equivalent sc. In a mathematics sense the topological equivalence model has the same fractals as the sc, which means that the sub-block and the block of the fcc are just the sc ones. Therefore, the equivalent critical point for the fcc can be represented by Equation (16) of the reference [3] , thus

In a similar way, the equivalent critical point for the bcc is given by

Substitution of Equations (4) and (5) puts Equations (7) and (8) into

2.4. Formation Equivalence
In the sc system there are infinite horizontal planes parallel to one another and infinite vertical planes relatively parallel, each lattice belongs to not only one horizontal plane but also one vertical plane. Such structure means that the sc is a direct sum of the square lattices (sq) [10] . The definition of the fractal dimensions of the sq is given by the reference [3] , if the fractal dimension of a sub-block of the sq is






A composite lattice cannot be homeomorphism to a simple lattice such as the sc, so we should seek another way. The d lattice as a composite structure can be described as two interpenetrating fcc lattices displaced along the body diagonal of the conventional cube by one-fourth of the diagonal length. The nearest neighbor lattices make up a diamond primitive cell, which is a simple cubic with one lattice at the cube’s center and the rest four lattices at its vertices, two of them on the top surface and the others on the bottom as shown by the figure 23 in the chapter 1 of the reference [11] . The nearest neighbor distance is 






3. Discussion
There has been no way to solve exactly the three-dimensional Ising models so far, except our theory [3] . In order to examine the above equivalence transformations we should introduce those data concluded by other theories. The approach of the series expansion can give us the critical points with high accuracy. Lundow and his colleagues calculated the critical points for fcc, bcc and d lattices on the base of the computing the critical point 






The magnitudes of the critical points in Equation (12) are greater than that they themselves compute, which may be related to the value of 






The magnitudes of the data in Equation (13) are also lager than the author’s. Using our theoretical results 


The behavior of the huge fluctuations attracted by a critical point shows the phase transition is irreversible, and the critical point is stable as being a minimum like a valley bottom between mountains. This critical property rules the principle of the method of series expansion in that the asymptotic value should finally go to a minimum after infinite iterating calculation. Such calculation, however, never been met in the practice, since the terms number in all of series expansions are always limited providing that the obtained values have to be regarded as results by man-made extension. This may be the cause that there are slight differences between the magnitudes of the critical points in Equation (14) from our theory and the ones out of the series expansions. An obvious example is the value of the 



An equivalence transformation itself does not result in any error, which comes from the initial values of 




The formation equivalence makes a composite lattice be simultaneously consistent of two or more lattice systems. Equations (9)-(11) lead to an algebraic expression 


Finally, we discuss simply about the critical exponents, which are relative to the series expansions. They should be regarded as the variables describing phenomenologically the critical behaviors without referring to the critical fluctuation mechanism. As we have found out that the heat capacity of a three-dimensional Ising model at the critical temperature is attributed to four types of spin phonons originating in the sub-blocks, the ordered blocks, the lattices in the sub-blocks, and the lattices in the ordered blocks [4] . Such a complicated mechanism cannot be radically represented by a single exponent. In fact, the critical exponents appear initially in the early investigation of the critical phenomena, they do be the phenomenological variables.
4. Conclusion Remark
We find two types of equivalence transformations among Ising models: the topological equivalence transformation and the formation equivalence transformation. These transformations make us investigate effectively more Ising models in structures, especially for the three-dimensional ones. With the help of our approach we have obtained exact critical points for the bcc, fcc, and d lattice spin systems.
References
- Liu, S.H. (1986) Solid State Physics, 39, 207-273. http://dx.doi.org/10.1016/S0081-1947(08)60370-7
- Havlin, S. and Ben-Avraham, D. (1987) Advances in Physics, 36, 695-798. http://dx.doi.org/10.1080/00018738700101072
- Feng, Y.-G. (2014) American Journal of Modern Physics, 3, 184-194. http://dx.doi.org/10.11648/j.ajmp.20140304.16
- Feng, Y.-G. (2014) American Journal of Modern Physics, 3, 178-183. http://dx.doi.org/10.11648/j.ajmp.20140304.15
- Feng, Y.-G. (2014) American Journal of Modern Physics, 3, 211-217. http://dx.doi.org/10.11648/j.ajmp.20140306.11
- Kramers, H.A. and Wannier, G.H. (1941) Physical Review, 60, 252-262. http://dx.doi.org/10.1103/PhysRev.60.252
- Onsager, L. (1944) Physical Review, 65, 117-149. http://dx.doi.org/10.1103/PhysRev.65.117
- Fisher, M.E. (1968) Physical Review, 113, 969-981. http://dx.doi.org/10.1103/PhysRev.113.969
- Schiff, L.I. (1968) Quantum Mechanics. 3rd Edition, McGraw-Hill, New York.
- Fulton, W. (1995) Algebraic Topology. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-4180-5
- Kittel, C. (2005) Introduction to Solid State Physics. John Willey & Sons, New York.
- Lundow, P.H., Markström, K. and Rosengren, A. (2009) Philosophical Magazine, 89, 2009-2042. http://dx.doi.org/10.1080/14786430802680512
- Sykes, M.F., Gaunt, D.S., Roberts, P.D. and Wyles, J.A. (1972) Journal of Physics A: General Physics, 5, 640-652. http://dx.doi.org/10.1088/0305-4470/5/5/005
- Domb, C. (1974) Ising Model. In: Domb, C. and Green, M.S., Eds., Phase Transitions and Critical Phenomena, Vol. 3, Academic Press, London, 357-484.
- Mouritsen, O.G. (1980) Journal of Physics C: Solid State Physics, 13, 3909. http://dx.doi.org/10.1088/0022-3719/13/20/013
- Deng, Y.J. and Blöte, H.W.J. (2003) Physical Review E, 68, Article ID: 036125. http://dx.doi.org/10.1103/PhysRevE.68.036125
- Feng, Y.G. (2005) Electronic Journal of Theoretical Physics, 7, 12-18.
- Wannier, G.H. (1945) Reviews of Modern Physics, 17, 50-60. http://dx.doi.org/10.1103/RevModPhys.17.50


