Received 10 October 2014; accepted 1 August 2015; published 5 August 2015

ABSTRACT

The Poisson-Laplace equation is a working and acceptable equation of gravitation which is mostly used or applied in its differential form in Magneto-Hydro-Dynamic (MHD) modelling of e.g. molecular clouds. From a general relativistic standpoint, it describes gravitational fields in the region of low spacetime curvature as it emerges in the weak field limit. For non-static gravitational fields, this equation is not generally covariant. On the requirements of general covariance, this equation can be extended to include a time-dependent component, in which case one is led to the Four Poisson-Laplace equation. We solve the Four Poisson-Laplace equation for radial solutions, and apart from the Newtonian gravitational component, we obtain four new solutions leading to four new gravitational components capable (in-principle) of explaining e.g. the Pioneer anomaly, the Titius-Bode Law and the formation of planetary rings. In this letter, we focus only on writing down these solutions. The task showing that these new solutions might explain the aforesaid gravitational anomalies has been left for separate future readings.

Keywords:

Astrometry, Celestial Mechanics, Ephemerides, Planets and Satellites: Formation

1. Introduction

“Speculations? I have none. I am resting on certainties.

I know whom I have believed and am persuaded that;

He is able to keep that which I have committed unto him against that day.”

―Michael Faraday (1791-1867)

The Azimuthally Symmetric Theory of Gravitation (herafter ASTG-model) set out in [1] [2] and preliminarily explored in the readings [3] -[5] is based on the Poisson-Laplace equation:

(1)

when we embarked on the ASTG-model, it was to seek for a plausible solution to the radiation problem thought to bedevil massive stars during their process of formation (cf. [6] -[13] , for the aforesaid radiation problem). In the present letter, and more that are (expected) to come, we continue the quest to seek further ground for the ASTG-model, i.e., demonstrating its latent power. We here lay down the ground work for further exploration by solving the time-dependent Poisson-Laplace equation. In addition to the Newtonian gravitational component, we generate four more gravitational components. These new components have the potential to solve the current existing gravitational anomalies such as the Pioneer Anomaly, the Moon-Earth [14] -[16] and Sun-(Moon-Earth) [17] [18] recession, Anomalous Rotation Curves of Spirial Galaxies (i.e., the so-called Darkmatter Hypothesis) and as well on the origins of the Tituis-Bode Law (whose origins remain a mystery) and the existence of ring systems around celestial bodies such as the Planet Saturn.

As argued in [2] , the ASTG-model is surely a new classical theory of gravitation which makes the seemingly ambitious hypothesis that the spin of a gravitating mass has a significant and decisive role to play in the emergent gravitational field of the spinning mass. The ASTG-model is based1 on the solutions of Equation (1), i.e.:

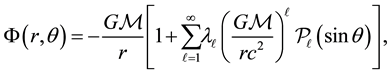(2)

where:

(3)

¹This theory can be extended to include the polar solutions. Exploration of these solutions is a task we hope to look into in future readings.

and are Legendre polynomials whose argument is and not as is usually the case and, is the mass of the central gravitating body, c is the speed of light in vacuum, r is the radial distance from this gravitating body, and are some dynamic parameters which in the ASTG-model are assumed to be related to gravitating body in question and the explicit dependence of these λ-parameters on the gravitating body’s spin have been explored and made clear in the reading [2] .

About the λ-parameters, it should be mentioned that this property that the λ’s are dynamic parameters assumed to be related to the gravitating body in question is the novelty of the ASTG-model. Putting weight to what we already have said, in a way, the dynamism of the λ-parameters makes the ASTG-model a new classical theory of gravitation where the spin of the gravitating mass enters the gravitational podium. Further, of the λ-parameters, for all conditions of existence, it is assumed that whenever spin is dropped and what this all means is that with the spin switched off, the ASTG-model reduces to the traditional Newtonian gravitational theory that we are used to know.

Furthermore, it should be mentioned that (as was done in the reading [1] ), the λ-parameters are free parameters whose dependence on spin and the resulting numerical coefficients are all to be determined from empirical data, intuition and imagination. This is clearly a weak point of the theory. We can only hope that the λ-parame- ters that we propose here will prove to be universal in that they will apply to other gravitational systems without the need for further adjustments.

The novel feature of the ASTG-model is that it brings the spin of a gravitating object into the fold of the classical gravitation (i.e., non-relativistic gravitation). The spin now plays an important and decisive role in generating the gravitational field that has a bearing on test bodies in the vicinity of this gravitating object. But the ASTG-model is not the only theory that does this. For example, we have the gravitomagnetic effects such as the Lense-Thirring Effect [19] [20] , the Gyroscope Precession Effect [21] -[23] and the Gravitomagnetic Clock Effect [24] -[32] . The ASTG-model is yet to be applied to these three important gravitomagnetic effects so as to see what it has to say about them.

Of these three important effects, the Pugh-Schiff Gyroscope Effect [21] -[23] has been measured to a convincing accuracy using University of Stanford’s2 Gravity Probe B Experiment [33] while the Lense-Thirring orbital precession was tentatively measured with artificial satellites orbiting some Solar system major bodies [34] -[45] . This Gravity Probe B measurement is one of the latest in a series of measurements that have confirmed the accuracy of the GTR. It places the GTR ahead of most of the competing models of gravitation. Nevertheless, it should be noted that in this regime of measurements, the GTR is being tested in the low energy regime and not in the regime of very high spacetime curvature where its predictions are clearly at variance with most of the competing models [46] -[48] . There is a need to test the GTR in regimes of high spacetime curvature if the short- comings of the GTR are ever to surface or any cracks in it are to emerge [46] -[48] , and these shortcomings may pave the way for alternative models of gravitation to demonstrate their supremacy (if any) in those regimes. Therefore, despite the accuracy with which the GTR is confirmed by experiments in the low energy regime, motivation to compare the GTR, experiment and alternative models remains not only high, but also necessary.

2. Theory

From a purely and strictly general relativistic standpoint, the Poisson-Laplace equation cannot be accepted as a true Law of Nature as it is neither Lorentz nor coordinate invariant for none-static gravitational fields i.e.. In this sense―i.e., of its none-general covariance, it is more like the highly successful Schrö- dinger equation, which is a down-graded version of a more generally covariant equation―the Klein-Gordon equation. Yes, the Schrödinger equation is successful, and true as-well is that, it does not meet the strict requirements of general covariance (one of the requisites of beauty for a theory), so it is only but a good approximation to the real Law of Nature that gives rise to it. It is just but a very good approximation.

Lorentz and coordinate invariance are held as sacrosanct minimum requirements for any law that seek the status of a Law of Nature. In order for the Poisson-Laplace Equation (1) to fulfill the Principle of Relativity, it is necessary to supplement it with a time dependent term, i.e.:

(4)

where (here and after) 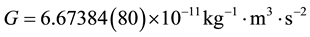is Newton’s universal constant of gravitation, 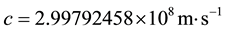is the universal speed of light in vacuum. In view of (4), the Poission-Laplace Equation (1) can be viewed as the case where. This law (i.e. 4), satisfies the Principle of Relativity as it can be derived from Einstein’s equation of gravitation as a first order approximation in the weak field limit [49] . This law published in 1915 by Albert Einstein (1879-1955) is given by:

(5)

where, is the Ricci tensor; R, is the Ricci scaler;, is the metric of spacetime;, is the matter stress-energy-momentum tensor; and;, is Einstein’s controversial cosmological constant which he introduced to “stop” the Universe from expanding. Here, we shall assume that this constant () vanishes identically (i.e.).

Now, in the weak field approximation, the metric is given by where is the flat spacetime Minkowiski metric and are the first order terms of the metric; inserting this into (5), one is led to:. In this weak field approximation, the dominant term is the 00-component of this equation, and these components, to first order approximation, they are given by and. Inserting these into, one is led to the four Poisson-Laplace Equation (4). Thus, if one accepts the Einstein field Equation (5), then, automatically, they also accept (4), thus this equation is an acceptable equation of gravita- tion.

From a purely general relativistic standpoint, this equation (i.e. (4)) is but an approximation only applicable in the weak field limit. The ASTG-model, together with the Four Poisson-Laplace theory here being advanced, are not a subset of Einstein’s General Theory of Relativity (GTR); see [50] . Inorder to accept (4), one merely has to accept it on the basis of requiring that the Poisson-Laplace equation obeys the Principle of Relativity and, that, it must submit to the general covariance principle. Besides, as shown in the reading [51] , the Equation (4) emerges from Maxwell-Heaviside gravitomagnetism which itself has been shown to emerge naturally from our proposed unified field theory of all the known forces of Nature [52] .

3. Derivation of the Field Potentials

As will be demonstrated shortly, an interesting feature of this law (i.e. Equation (4)) is that the time dependent potential can be associated or attributed to a time variable gravitational constant. To see this, we have to solve the equation first. We will do so by separation of variables in Section 3.1 where three solutions will be obtained. In Section 3.2, we shall solve this same equation for two none-separable solutions. In total, five solutions are obtained. In solving this equation (i.e. Equation (4)), we shall do is to solve the empty space equation, i.e.. This empty space equation applies for the case where the mass of the central gravitating body is constant. To obtain a solution for the case where a star or the gravitating mass is immersed in a pool of gas like, e.g., a star inside a core where the mass is dependent on the radial distance i.e., what one needs to do is to replace in the empty space solution with:

(6)

i.e.. The arguments justifying this have been laid down in [4] .

3.1. Separable Solutions

As afore-stated, our focus in this letter is on the radial solutions, thus we are going to solve the equation, only for the radial solutions by the method of separation of variables where. From this, it follows that:

(7)

where is a dimensional constant with units of m⁻¹. Obviously, this differential Equation will have to be solved for three cases, i.e.. The constant is a universal constant because it depends neither on any of the space coordinates, nor time (t). Clearly, because of this non-dependence on space and time coordinates, this constant must be an important universal and fundamental constant of Nature, having (perhaps) the same status as, e.g., the speed of light c. In the subsequent section, we will consider separately the cases, and where the first three solutions are laid down and in Section 3.2 the last two solutions are presented. For easy referencing, we are going to label them with a subscript which runs from 1 to 5 i.e..

3.1.1. First Gravitational Component: (μ² = 0)

Newtonian Component. In the light of the time dependence just introduced in the Poisson-Laplace equation, we are forced to formally go through the “derivation” of the Newtonian gravitational potential, albeit, with the important difference that the gravitational constant forthwith seizes to be a constant; it is now time dependent. Assuming separability i.e., the radial solution of (7) is the well known Newtonian gravitational potential, i.e.:, where (here and after) is the mass of the gravitating body in question and r is the radial distance from this body. The solution to the time dependent part is, where are constants. Since, it follows that:

(8)

From the above, clearly, the time dependent component of the gravitational field can be absorbed into the gravitational constant G as follows:. This means, we can now write (8) with the linear time dependent term having been absorbed into the gravitational constant as follows:

(9)

where, as part of the labelling scheme stated earlier, we now have inserted the subscript “1” onto and. Now, if is the gravitational constant when the cosmic time was equal to zero, and is the time rate of change of the gravitational constant, it follows that:

(10)

For the first gravitational component, throughout this letter, shall represent the gravitational constant when the cosmic time was equal to zero, and the time rate of change of the gravitational constant. Because naturally we expect that the strength of the gravitational force should diminish with time; for this to be so, we must have.

3.1.2. Second Gravitational Component: (μ² > 0)

Pioneer Component (I) (Yukawa Potential). Rather in an ad hoc manner, the Yukawa type gravitational potential has long been considered as a possible cause of the Pioneer anomaly [53] -[56] and a contender to explaining the seemingly anomalous rotation curve of galaxies [57] [58] . In all these considerations, no fundamental justification for the Yukawa type potential has been put forward; thus far, the only justification is compliance with empirical evidence. What we shall do here is basically give justification for them. We believe that this will give credence to the efforts [53] - [58] where the Yukawa potential has been introduced in a rather ad hoc manner to explain the Pioneer anomaly and the seemingly anomalous rotation curves of galaxies. In the afore-cited studies, the gravitational potential is given by:

(11)

The Pioneer anomaly and rotation curves of galaxies is then explained by the extra Yukawa term. In the Yukawa term and are constants that are determined by fitting the theory to the data. The question is: “Other than the fact that this term can fit the data, is there any fundamental justification for this ad hoc term? Can it be derived rather than inserted via the sleight of hand?” As stated, our core-mission in this section is to justify its inclusion in matters of gravitation by deriving it from some credible soils of gravitation.

Now, without wasting much time and space, assuming separability i.e., the solutions to (7), are:

(12)

where are constants. If, we will obtain a gravitational potential that is not in tandem with physical and natural reality as we know it because the terms with the coefficients will lead to a gravitational field that only gets stronger with increasing distance and the progression of time. To avoid this, we must have. Now, we shall make the setting where is the associated gravitational constant at time. Further setting and putting everything together, the gravitational Yukawa potential should then be given by:

(13)

In a future reading that only awaits the publication of the the present letter, it will be shown that the potential, together with; can in-principle explain the Pioneer anomaly. In anticipation, we have coined these two potentials Pioneer Component (I) and (II) respectively.

3.1.3. Third Gravitational Component: (μ² < 0)

Planetary Ring Component. We are now going to generate our third gravitational component. This component gives rise to a ring structure around a central massive gravitating body. These rings are such that they are equally spaced. Given this, and as-well that planets not do exhibit such an even spacing, this ring structure “can not explain” the origins of planets as we know them. If one can conceive of the possibility that in those places where a ring is expected and there is none, then, hypothetical, this ring is considered missing, then, the theory has not failed but predicted a missing ring. That said, let us go onto the derivation of this gravitational component.

As one can verify for themselves, the general solution to (7) under the constraint (μ² < 0), is:

(14)

where is the magnitude of: remember is a complex number, hence. Now, because and must be real, we must have and. With this setting, one will have the complex parts of being identically equal to zero. Let us set, so that the final solution is:

(15)

where. Making a brief snap-shot of this solution, we note that, in space, this potential has its minimum-points when and, this occurs when. From Lagrangian mechanics, we know that a system will tend to settle in regions where its Lagrangian is minimum. One can easily show that the regions defined by the rings:

(16)

where; will be regions of minimum Lagrangian, therefore, matter will tend to settle in these rings

thus giving rise to a ring structure, hence, the potential (15) should most certainly explain the existence of rings around planetary bodies such as the planet Saturn. Certainly, it will be interesting to know if this component will be able to explain stellar ring systems. The task for this exploration has been slated for a future reading. In hopeful anticipation, we have called this component the Planetary Ring Component.

With regard to a sinusoidally varying G, is it important to mention here a very interesting development, that is, using about a dozen measurements of Newton’s universal gravitational constant, G; that is, Earth-based laboratory measurements which have been made since 1962, Anderson et al. [59] notes that these measurements have yielded values that differ by far more than their reported random plus systematic errors. By plotting these measurements against time, Anderson et al. [59] unearthed an interesting behaviour associated with these measurements―they find that these values for G have a well behaved oscillatory nature, with a period of, and an amplitude of. The mean-value crossings occur in 1994 and 1997.

Somewhat in the footsteps of the great German physicist Max Karl Ernst Ludwig Planck (1858-1947) who was reluctant to embrace the revolutionary idea of the quanta that he had discovered in 1900; instead of embracing this potentially landmarking discovery, Anderson et al. [59] distance themselves from claiming that their discovery is a discovery to do with the actual variation of the gravitational constant G. They conservatively hold that G can not actually vary by this much, this quickly, but instead that something in the measurement process is varying. Anderson at al. [59] ’s scepticism is not shared by all. From the present findings, it is, it is very possible that Anderson at al. [59] ’s discovery is potentially revolutionary in nature. We are currently working out the meaning of this discovery in relationship to the present ideas.

3.2. None Separable Solutions

If one was only seeking separable solutions, then, they would have to end with the solution. With the two “new” solutions and, they will―at least; be in a position to justify the inclusion of the Yukawa potential in gravitational physics and as-well to explain the existence of planetary rings. They will however find themselves not in a position to consistently explain the Pioneer anomaly and the rotation curves of galaxies; and as-well, the Titius-Bode Law that posits the logarithmic placing of planets in planetary systems.

As will be shown shortly, there exists two none-separable solutions. For these none-separable solutions we assume where is the part with the none separable space and time coordinates. The none-separable part is such that:

(17)

where is a dimensionless constant and the none-separable part is given by:

(18)

The none separable space and time function is such that:

(19)

where is a constant. This solution belongs to the gravitational constant. Therefore, and will both have a spacial and temporal variation. Now, in the subsequent sections, we shall consider the two cases (ν² > 0 and ν² < 0).

3.2.1. Fourth Gravitational Component: (ν² > 0)

Pioneer/Darkmatter Component (II). Let us set, where α is some dimensionless quantity. Now, from this relationship, it follows that:

(20)

The two solutions of α are represented by. Note that for a real ν, the discriminant of (20) [i.e. the term, under the square root sign] is positive definite.

Our step in solving (17) and (18) is the following: (1) We solve for in (17). (2) We know that the general solution to this equation in the case, is:

(21)

where is a constant with the dimensions of length and (A, B) are some dimensional constants. (3) The next step now is to introduce a time dependence into this expression i.e., by numerically solving for in (18). Off cause, as stated, we are not going to do conduct this exercise by assume that this solution exists. (4) The is step is to set and. Now, since, it follows that this solution can be written as:

(22)

where and the dimensionless parameter is such that.

As will be seen a future reading that tackles the Pioneer anomaly, the potential―together with, can in-principle, explain the Pioneer anomaly, hence we have termed it [i.e.] the Pioneer Component (II). Now, we proceed to the fifth and final solution. It is for this reason that we strong believe this gravitational potential must exist. Off cause, for it to exist, it must flow from a legitimate equation [such as (4)] from which gravitational potentials can be derived.

3.2.2. Fifth Gravitational Component: (ν² < 0)

Titius-Bode Component. As before, let us set where we strictly assume that. Now, from the foregoing, it follows that:

(23)

where and are the two solutions. Now, to achieve our desired objective, we proceed by substituting into:

(24)

In this solution, we shall drop the term whose coefficient is B. The reason for doing this is that this term will only add a phase factor in the final solution―so, to save space, we have to drop it. Now, let us set. The resultant potential is:

(25)

Using the relation, Equation (25) can be written as:

(26)

Since and from the Euler relation, if follows that becomes:

(27)

where. As was done with, the function must be subject to the constraint (18). The phase factor has been added to take into account the term in whose coefficient is B. It will be shown in a future reading that the solution (27), can in-principle, explain the Titius-Bode Law which hypothesis that planets follow a logarithm spacing from their central star (for an exposition of this rather strange “law”, see e.g. [60] -[62] ).

4. Lorenz Gauge and the Newtonian Gravitational Constant

The gravitational constants are all time variable and in the case of the non-separable case, they have a spatial dependence as-well. If further constraints could be found, it may be possible to restrict these constants even to a point where they become true constants with no time and or space variation. Thus far, we have no way to make further restriction that may tell us for sure Nature decided to have these constants as time variable. In-order to decided on whether or not the Newtonian gravitational constant G, we are going to appeal to the modified Lorenz gauge set out in [52] [63] .

As already said in Section 2 is that it has been shown in the reading [51] that the Equation (4) emerges naturally from gravitomagnetism which is itself emerges from our proposed unified field theory [52] . There are many gravitomagnetic approaches in existence today and the proposed approach in [51] [52] is just one amongst these. We will not waste time by comparing our approach with other approaches―this we find as unnecessary. Our disposition here is to obtain the natural solution of (4) and link all of them to the gravitational phenomenon.

As in electromagnetism, it is demonstrated in the readings [51] [52] (and references therein), that the gravitational field submits to a four vector description as is the case with electromagnetism. This four vector we have proposed therein [51] [52] that it obeys a modified Lorenz gauge condition. In electromagnetism, the Lorenz gauge condition is generally used in calculations of time-dependent electromagnetic fields through retarded potentials [64] ; is the aforesaid four-potential. The Lorenz gauge condition has the advantage of being Lorentz invariant. This Lorentz invariance is important because we expect all our theories to obey Lorentz symmetry. Our proposed new Lorenz gauge condition is that, where is a non-zero (see [51] [52] ).

If is in (7) we have, then, to first order in the time derivative we can naturally only have:

(28)

From (28), it follows that the modified Lorenz gauge condition, becomes:

(29)

From this equation, the most natural solution to this equation for is:

(30)

What we are really concerned about here is (28). Other than the Lorenz gauge, this Equation (28) gives us an extra constant constraint on μ. For the cases (), nothing changes about the time variability of the constants G₂, G₃, G₄, and G₅; they remain unaltered. However, for the case (), G₁ becomes a pure constant without any time variation because the Newtonian gravitational potential Φ₁ is static since (28) tells us that if (), we must have ().

With regard to a time variable-G (i.e., the Newtonian gravitational constant), recent research has shown that, at least for the last 9 billion of the Universe’s assumed 13.8-billion-year history, the Newtonian gravitational constant G has not varied more than (at most) one part in a billion. This result is obtained after an exhaustive study of about 580 observed supernovae events by Professor Jeremy Mould and his Ph.D. student Syed Uddin at the Swinburne Centre for Astrophysics and Supercomputing and the ARC Centre of Excellence for All-Sky Astrophysics. Their research findings show that the Newtonian constant G has not changed appreciably over cosmic time. This research which focused on Type 1a supernovae, demonstrated a constant G within an upper bound of [65] . If as suggested here that, then experiments such as those of Professor Jeremy Mould [65] , these experiments; as is the case with the issue of whether or not a photon has mass (see e.g. [66] ), they will not yield any conclusive answers as one experiment to the other, researchers will only push the measurements to the next decimal place.

5. Multi-Component Gravitational Field

The five solutions i.e. Equations (9), (13), (15), (22) & (27) all emerge from the Equation (4), they are thus legitimate gravitational potentials. The questions is, “How does Nature select one solution over the other?” We hypothesize that Nature employs all the five solutions concurrently on every gravitating body at al-times. If this is the case, the total gravitational potential is then given by a superposition of all the five potentials, i.e.:

(31)

Written in full, the total radial gravitational potential is as given by:

(32)

In this expression (32), , is defined as:. In this formula (32),. Of the five gravitational components i.e., obviously, the Newtonian gravitational component () must be the dominant component in (32). If this total potential (32) is totally with reality, then, the other components should act in such a manner as to give structure formation on the Solar and perhaps galactic scale.

6. General Discussion

This letter has shown that the Four Poisson-Laplace Equation (4) has five radial solutions. According to the order of our presentation, the first of the five solutions is the usual Newtonian law of gravitation. The other four are very interesting as they hold the promise to answer questions on a number of gravitational anomalies including the formation of structure in the Universe. In the present letter, our thrust has mainly been to present these solutions so as to lay down the ground for future exploratory work on these solutions.

An interesting outcome of the Four Poisson-Laplace Equation (4) is that the gravitational constant G emerges as a time dependent constant. Since it was first proposed that the gravitational constant G might vary with time [67] [68] , there has never been a solid theoretical foundation to furnish this hypothesis. If what we have presented is anything to go by―as we strongly believe it to be; then, the foundations of a time variable G have been found. Not only does the Four Poisson-Laplace Equation (4) predict a time variable-G, it also predicts about three forms of G (linear, exponential and sinusoidal). Further, for the gravitational constants associated with the none-separable solutions, it is seen that these constants have a spatial dependence. In-closing, we would like to say that, more will be presented follow-up research articles the deal with the Pioneer Anomaly, Darkmatter and the Titius-Bode Law.

7. Conclusion

Other than the Newtonian component, the gravitational force may contain four more components and these components may―as hinted herein―explain a number of mysteries such as Darkmatter, the Pioneer Anomaly, origins of the Titius-Bode Law and the emerges of structures such as planetary ring systems.

Cite this paper

Golden GadzirayiNyambuya, (2015) Four Poission-Laplace Theory of Gravitation (I). Journal of Modern Physics,06,1195-1206. doi: 10.4236/jmp.2015.69124

References

NOTES

²See Gravity Probe B. Websites: http://einstein.stanford.edu and http://www.gravityprobeb.com.