Journal of Modern Physics
Vol.05 No.15(2014), Article ID:49779,5 pages
10.4236/jmp.2014.515142
Measurement of Photon-Induced L X-Ray Fluorescence Cross Sections for Ho and Yb in the 16.04 - 24.68 keV Energy Range
Hussein Al-Taani1, Nasr Saleh1, Kamal Al-Saleh2
1School of Natural Resources Engineering and Management, German Jordanian University, Amman, Jordan
2Department of Physics, University of Jordan, Amman, Jordan
Email: hussein.taani@gju.edu.jo, naser.Saleh@gju.edu.jo, k.saleh@ju.edu.jo
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2014; revised 9 August 2014; accepted 31 August 2014
ABSTRACT
Lα, Lβ, and Lγ X-ray fluorescence cross sections for Ho and Yb have been measured at various incident photon energies in the energy range 16.04 ≤ E ≤ 24.68 keV. The measurements have been done using an X-ray tube with a secondary-excitor system of Zr, Nb, Mo, Cd, and In. The experimental values of the cross-sections were determined by measuring the absolute yield of L subshell X-rays emitted from a standard target of a given energy. Theoretical tabulated values of subshell photoionization cross-sections, fluorescence yields, Coster-Kronig transition probabilities and radioactive decay rates have been used to calculate the theoretical values of the cross-sections. The experimental results of the cross-sections at various excitation energies have been compared with theoretically calculated values. Fairly good agreement is obtained between the present experimental results and the calculated values.
Keywords:
L X-Ray Fluorescence, Cross Section

1. Introduction
A large variety of measurements of photoionaization cross section at photon energies from 5 keV to 1 MeV in different elements with atomic numbers 22 ≤ Z ≤ 92 have been reported in literature [1] -[8] . Information on L X-ray cross sections, for different elements and various photon energies, is important because of their widespread use in the fields of atomic, molecular, radiation physics, in nondestructive elemental analysis by X-ray emission technique and basic studies of nuclear and atomic processes. L X-ray fluorescence cross sections are also important for developing highly reliable theoretical models describing the fundamental inner shell processes. For example, the theoretical photoionization cross-sections can be converted into X-ray production cross-sec- tions using the tabulated values of fluorescence and Coster-Kronig yields, and then compared with the experimental values, thereby providing an indirect check on the accuracy of both the theoretical calculations of the photoionization cross-sections and the yields [9] -[12] .
L X-ray fluorescence cross-sections and their intensities can be calculated by using photoelectric cross-sec- tions, fluorescence yields, and fractional emission rates. Uncertainties in these tabulated quantities largely reflect the error in L X-ray fluorescence cross-sections. For this reason most users prefer the experimental values of the cross sections whenever large discrepancies are observed between theoretical and experimental values [11] .
An X-ray tube with a secondary target arrangement is used, in which the primary radiation generated by the electrons is used here to excite the secondary target. In this process the major part of bremsstrahlung radiation generated by X-ray tube is eliminated, and the radiation from the secondary target has a high degree of monochromatization with high intensity. Rao [11] has reported L X-ray fluorescence cross-sections (σL) for elements in the atomic region of 46 ≤ Z ≤ 51, excited by photons of energies 6.47, 7.57, and 8.12 keV.
Mann [13] measured Ll, Lα, Lβ, and Lγ X-ray production cross-section by 59.57 keV photons for elements of 57 ≤ Z ≤ 68 and earlier for 73 ≤ Z ≤ 92. However, they [13] have concluded that the uncertainties in the measured cross section of their latest work were 6% - 8% due to counting statistics and errors in determining various parameters. Earlier experimental L X-ray cross-sections were measured using radioisotopes as excitation sources [14] -[19] . They have the advantages of stable intensity and a well-defined energy, and small size, which allows compact, and efficiency geometry, and they operated without any external power. The drawbacks are the small number of suitable radioisotopes available at different excitation energies, the decline of intensity with time if the half-life is of the order of a few years or shorter, and the low relative fluency rate.
The present measurements have been performed with an X-ray tube with secondary exciter systems as an excitation source. L X-ray cross-sections measurements using X-ray tube have been reported in literature. The K X-rays of Zr, Nb, Mo, Cd, and In, secondary exciters provided sources of photons with energies of: 16.04, 16.90, 17.78, 23.62 and 24.68 keV, respectively. In the present study, Lα, Lβ, and Lγ X-ray production cross-sections were measured for Ho and Yb at the above mentioned photon excitation energies.
2. Experimental Arrangement
The experimental arrangement and geometry used in the present study are shown in Figure 1. The primary excitation source contained X-ray tube with a Mo anode whose maximum voltage and current were 55 kV and 60 mA, respectively. The tube operating voltage can be varied between 20 and 55 kV and secondary target was excited at an operating voltage of 25 kV with a current of 5 mA.
The direct beam from the X-ray tube was incident on the secondary target (called exciter). The secondary exciters of Zr, Nb, Mo, Cd, and In were pure metal sheets about 0.5 mm thick (purity of 99.99%). The secondary
Figure 1. Schematic set-up of the X-ray fluorescence spectro- meter employing an X-ray tube with secondary target. 1 = X-ray tube; 2 = collimator; 3 = secondary target; 4 = cylindri- cal collimator covered by filter material of secondary target; 5 = sample; 6 = detector collimator; 7 = detector.
radiation leaving the target was collimated through a cylindrical collimator with a transmission filter of the same secondary target material, in order to avoid undesirable radiation of the photoelectric effect of the secondary radiation in the collimator and to improve the monochromaticity of the beam. The samples were placed at 45o angle with respect to the direct beam from the secondary exciter. The fluorescent X-rays from the sample were then detected by the collimated Si(Li) detector having a thickness of 5 mm and an energy resolution of 185 eV at 5.9 keV. The output from the preamplifier was driven to a shaping amplifier with a pulse pile-up rejection capability and fed to a multichannel-analyzer interfaced with a personal computer provided with suitable software for data acquisition and peak analysis.
3. Experimental and Theoretical Approach
The values of the experimental L X-ray fluorescence cross-section can be calculated from the measured quantities using the equation:
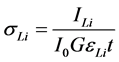 (1)
(1)
where ILi is the observed intensity (area under the photo peak in counts per seconds) corresponding to the Li group of X-rays, Io is the intensity of incident radiation, G is the geometrical factor, εLi is the detection efficiency for the Li group of X-rays, and t is the thickness of the target in g/cm2. Thus, knowing the product Io G εLi one can determine the absolute values of the X-ray fluorescence cross-sections. However, the value of Io G εLi, which contains terms related to the incident photon flux, geometrical factor and the absolute efficiency of the X-ray detector, was determined by collecting the K X-ray spectra of thin standards of Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ge, Se, and Br using the equation [9] :
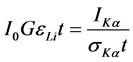 (2)
(2)
where IKα, Io and εKα have the same meaning as in Equation (1) except that they correspond to K X-rays instead of the ith group of L X-rays. Theoretical values of σKα X-ray fluorescence cross-sections were calculated using the equation [9] :
 (3)
(3)
where σ(E) is the K-shell photoionization cross-section [20] for the given element of excitation energy E, ωK is the K-shell fluorescence yield [12] and FKα is the fractional X-ray emission rate for Kα X-rays and is defined as:
 (4)
(4)
where IKα and IKβ are the Kα and Kβ X-rays intensities, respectively [21] . Since the experimental values were not available for all elements, it was decided to use the theoretical values to obtain Io G εKα. The factor Io G εKα was fitted as a function of energy using the equation:
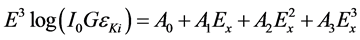 (5)
(5)
where Ex is the Kα X-ray energy and Ao, A1, A2, A3 are constants evaluated from the least-squares fitting. The values of the factor IoGεLi for each L X-ray line of average energy ELi are extrapolated from Equation (5).
For a particular element, the X-ray cross-sections σi(E) (i = Kα, Kβ, Kγ, Lα, Lβ, Lγ) at a required energy E was obtained from the tabulated values using logarithmic interpolation. More details can be found in our previous work [9] .
The values of L X-ray fluorescence cross-sections were calculated from the theoretical sub-shell photoionization cross-sections [20] , radiative decay rates [22] , semi-empirically fitted values of fluorescence yield and Coster-Kronig transition probabilities using the following equations:
 (6)
(6)
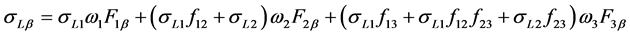 (7)
(7)
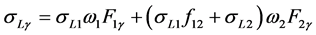 (8)
(8)
where σL1, σL2 and σL3 are sub-shell photoionization cross sections of the elements at the excitation energy; ω1, ω2, and ω3 are L sub-shell fluorescence yields; f12, f13, and f23 are the Coster-Kronig transition probabilities, and Fny (F3l, F3α, F3β, etc.) are the fraction of the radiation width of the subshell Lη (LI, LII, LIII) contained in the y-th spectral line, i.e.
 (9)
(9)
where Γ is the theoretical total radiative transition rate of the L3 shell and Γ3α is the sum of the radiative transition rates which contribute to the Lα lines associated with the hole filling in the L3 shell. That is,
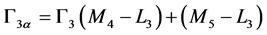 (10)
(10)
where Γ3 (M4 – L3) is the radiative transition rates from the M4 to the L3 shell. The radiative transition rates for many elements have been calculated by Scofield [21] [22] who applied the relativistic Hartree-Slater theory with a central potential and included the retardation effect.
4. Results and Discussion
The measured values of L X-ray fluorescence cross-sections for Ho and Yb at different incident photon energies have been plotted as a function of incident photon energy and are shown in Figure 2(a) and Figure 2(b). Further details of these calculations are given elsewhere in our previous work [9] . The measured values of cross- section are in fairly good agreement with the predicted values.
According to Equation (1) the overall error in the measurement L X-ray fluorescence cross-section is estimated to be around 8%, except for the L X-ray line around 10%. The estimated error in measured cross-sections arises from the uncertainties in the various physical parameters (Table 1) required evaluating the experimental results using Equation (1), further details are given in [9] . The error in the values of L-subshell Coster-Kronig transition probabilities fij is between 10% to 20%, and 3% - 15% is the error in the tabulated values of L-subshell fluorescence yields. The error in the final value of L X-ray fluorescence cross-section can rise up to 20% due to the uncertainties in ωi and fij.
The systematic error in the experimental measurements or the error in the calculated values of the physical parameters (σLi and/or Fny) used to evaluate the theoretical L X-ray fluorescence cross-sections can be the reason of disagreement between the experimental and theoretical results.

Figure 2. Comparison of measured and theoretically calculates Lα, Lβ, Lγ X-ray cross-sections as a function of energy for: (a) Ho; (b) Yb. Experimental values are indicated as: Lα open squares, Lβ solid squares, Lγ stars. Calculated values are represented as: Lα solid curve, Lβ dashed curve, and Lγ dash-dot curve.
Table 1. Uncertainties in the quantities used to determine L X-ray fluorescence cross-sections in Equation (3).
Theoretical values of L-subshell photoionizations cross-sections have been taken from the latest available tabulations. The error in these tabulated values is less than 0.1%. No reliable experimental results for L-subshell photoionization cross-sections are available. Also, experimental and theoretical results of total-atom photoionization cross-sections above 100 keV are in good agreement, with an uncertainty of a few percent.
The values of parameters such as fluorescence yields and emission rates need to be measured accurately. These parameters based on relativistic Dirac-Hartee-Slater theory need to be calculated for all the elements in question in order to check the validity of the theory in this atomic region. However, for trace elemental analysis using a fundamental approach, one should use experimental values of L X-ray fluorescence cross-sections since they involve an error around 8%, whereas, theoretical values of L X-ray fluorescence cross-sections can have an error of up to 20% [21] [22] . L X-ray fluorescence cross-sections need to be measured using more elements covering a wider range of energy.
References
- Seven, S. (2012) Radiation Physics and Chemistry, 81, 489-494. http://dx.doi.org/10.1016/j.radphyschem.2012.01.032
- Demir, D. and Sahin, Y. (2007) X-Ray Spectrometry, 36, 178-184. http://dx.doi.org/10.1002/xrs.941
- Bennal, A., Shidling, P., Badiger, N., Thontadarya, S. and Hanumaiah, B. (2005) American Journal of Physics, 73, 883. http://dx.doi.org/10.1119/1.1881254
- Sahin, M., Demir, L., Sögüt, Ö., Ertugrul, M. and Içelli, O. (2000) Journal of Physics B: Atomic, Molecular and Optical Physics, 33, 93. http://dx.doi.org/10.1088/0953-4075/33/1/309
- Baydaş, E., Söğüt, Ö., Şahin, Y. and Büyükkasap, E. (1999) Radiation Physics and Chemistry, 54, 217-221. http://dx.doi.org/10.1016/S0969-806X(98)00265-5
- Ertuǧrul, M. (1996) Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 119, 345-351. http://dx.doi.org/10.1016/0168-583X(96)00357-6
- Singh, N., Mittal, R., Allawadhi, K. and Sood, B. (1987) Journal of Physics, B 20, 5639-5645. http://dx.doi.org/10.1088/0022-3700/20/21/014
- Garg, M.L., Mehta, D., Verma, H.R., Singh, N., Mangal, P.C. and Trehan, P.N. (1986) Journal of Physics B: Atomic, Molecular and Optical Physics, 19, 1615-1622. http://dx.doi.org/10.1088/0022-3700/19/11/016
- Al-Saleh, K. and Saleh, N. (1999) Radiation Physics and Chemistry, 54, 117-124. http://dx.doi.org/10.1016/S0969-806X(98)00252-7
- Durak, R., Erzeneoǧlu, S., Kurucu, Y. and Şahin, Y. (1998) Radiation Physics and Chemistry, 51, 45-48. http://dx.doi.org/10.1016/S0969-806X(97)00088-1
- Rao, D., Cesareo, R. and Gigante, G. (1994) Nuclear Instruments and Methods in Physics Research Section B, 86, 219- 224. http://dx.doi.org/10.1016/0168-583X(94)95281-7
- Krause, M., Nestor, C., Sparks, C. and Reicci, E. (1978) Oak Ridge National Laboratory Report ORNL/5399.
- Mann, K., Mittal, R., Allawadhi, K. and Sood, B. (1991) Physical Review A, 44, 2198. http://dx.doi.org/10.1103/PhysRevA.44.2198
- Rao, D., Cesareo, R. and Gigante, G. (1993) Physical Review A, 47, 1087. http://dx.doi.org/10.1103/PhysRevA.47.1087
- Puri, S., Chand, B., Garg, M., Singh, N., Hubble, J. and Terhan, P. (1992) X-Ray Spectator, 21, 171-174. http://dx.doi.org/10.1002/xrs.1300210405
- Singh, S., Chand, B., Mehta, D., Kumar, S., Garg, M., Singh, N., Mangal, P. and Terhan, P. (1989) Journal of Physics B, 22, 1163. http://dx.doi.org/10.1088/0953-4075/22/8/009
- Garg, M., Mehta, D., Verma, H., Singh, N., Mangal, P. and Terhan, P. (1986) Journal of Physics B, 19, 1615. http://dx.doi.org/10.1088/0022-3700/19/11/016
- Shatendra, K., Allawadhi, K. and Sood, B. (1985) Physical Review A, 31, 2918. http://dx.doi.org/10.1103/PhysRevA.31.2918
- Chang, C. and Su, W. (1978) Nuclear Instruments and Methods, 148, 561-566. http://dx.doi.org/10.1016/0029-554X(78)91039-X
- Scofield, J. (1973) U.C.R.L. Report: 51326. Lawrence Livermore Laboratory Report, Livemore.
- Scofield, J. (1974) Atomic Data and Nuclear Data Tables, 14, 121-137. http://dx.doi.org/10.1016/S0092-640X(74)80019-7
- Scofield, J. (1969) Physical Review, 179, 9. http://dx.doi.org/10.1103/PhysRev.179.9




