Journal of Modern Physics
Vol.5 No.12(2014), Article
ID:47747,17
pages
DOI:10.4236/jmp.2014.512108
The Twins Clock Paradox History and Perspectives
Robert L. Shuler Jr.
NASA Johnson Space Center, Houston, TX, USA
Email: robert.l.shuler@nasa.gov, mc1soft@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 6 May 2014; revised 2 June 2014; accepted 27 June 2014
ABSTRACT
The twins or clock paradox has been a subject of lively discussion and occasional disagreement among both relativists and the public for over 100 years, and continues to attract physicists who write papers giving new analyses or defending old ones, even though many physicists now consider the matter only of educational interest. This paper investigates the number of papers, which is increasing, and trends in explanations, some of which are now targeted at professional physicists and other of which are targeted at optical or radar visualization rather than problem solving. Observations of students indicate that the latest techniques help but only somewhat. An analysis is made of 21 previous treatments appearing in the education related American Journal of Physics, Einstein’s discussions and several other pedagogical papers. A new memory aid for simultaneity transformation is given that puts it on a par with “time dilation” and “length contraction” for quick and easy problem visualization. The point of view of a trailing twin is introduced to show how simultaneity changes account for missing time in the turnaround. Length contraction is treated on equal footing with time dilation, and Swann’s insight into clocks is extended to lengths. Treatments using the conventionality of simultaneity are seen as equivalent to choice of co-moving frames. Responses to difficult questions are suggested which avoid being dismissive, and engage students’ critical thinking.
Keywords:Clock Paradox, Length Contraction, Simultaneity, Special Relativity, Time Dilation, Twins Paradox

1. Introduction
A puzzled colleague wrote to the author recently regarding the twins paradox, “On the one hand, I think that the situation is well understood, and adequately explained in plenty of textbooks. On the other hand… there are complementary explanations which take different points of view on the same underlying space-time geometry (though, alas, the authors don’t always seem to realize this, which rather undermines my assertion that the effect is well enough understood)”.
Perhaps my friend overstates, but there is no doubt at any rate that the twins or clock paradox continues to fascinate and confuse the public and physics students. Much of the literature seeks more effective ways of explaining or visualizing Special Relativity (SR). Though SR does not actually convey longer life experience, the ability to affect clocks, presumably in some explanations remote clocks, seems magical. What causes this effect? Is it the acceleration or the travel at high velocity? Even after 108 years, it can seem to depend on which paper one reads.
About 200 peer reviewed academic papers with clock paradox or twin(s) paradox in their title can be identified since 1911, most of them since 1955. A partial histogram by decade of appearance is shown in Figure 1. Except for the running controversy with H. Dingle printed largely in Nature in the 1950s and 1960s, the literature surveyed can be considered to be largely accepting of and friendly toward SR. Fewer than a dozen articles based on an ether theory (mostly older) or some sort of cosmological reference (a relatively new trend) made it through this filter. So the data sample represents a community of people one would expect to be in agreement after at most a few initial years of back and forth.
Seventeen percent of these papers appeared in the American Journal of Physics or its sister publications. A dozen articles or notable letters appeared in Nature. Only 4 have appeared in the Physical Review family of journals, some of which were related to experimental tests. The large percentage in AJP appears to be related to that journal’s connection with the teaching of physics.
Though the correct answer has never been in doubt the matter of how to explain the traveling twins appears to be far from settled. After a flurry of activity in the late 1950s and early 1960s, perhaps related to the dawn of the space age, there has been steady almost exponential growth in the number of papers, with about 6 appearing annually for the past decade. The trend appears set to continue despite the implication in many of these papers that the matter is settled. This cannot be just the ego-centric views of the authors, because virtually all of these papers are peer reviewed and some appear in very selective journals. In other words, the trend reflects not just the views of authors but of a larger community of reviewers and editors as well. An outside observer might reasonably conclude there is a deep conviction that the matter should have been settled, along with a nagging suspicion that it is not. Meanwhile, a paper on student problem solving (which we will discuss) suggests that the latest methods may be helping some but still fall short.
The problem is described as follows. There is a pair of identical twins, or clocks. One is left on Earth, and the other goes on a long space voyage. For dramatic effect the voyage is often described as being at very high speed, but it is actually only necessary that it be long or that the clocks be of high accuracy. According to SR, each sees the other as moving, illustrated in Figure 2, and therefore the other’s clock is slow. When they get back together, who is right?
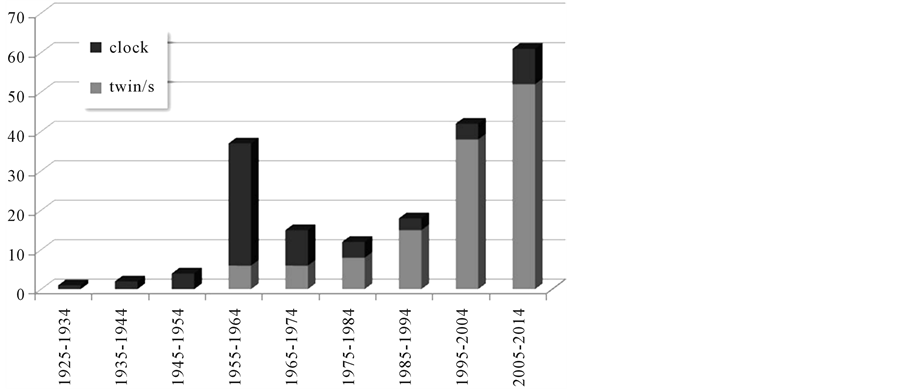
Figure 1. Academic papers with clock paradox or twin(s) paradox in title.
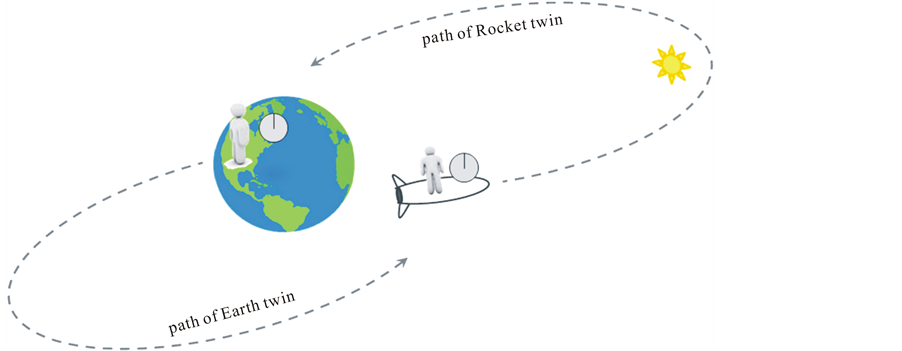
Figure 2. Each twin sees the other as moving away and back.
Experts have debated whether to use the word paradox at all. There is a clear asymmetry in that only one twin accelerates. This discussion conceals the main point, which is that within SR there is perfect symmetry between relatively moving observers and students do not understand how observers can mutually view each other’s clocks as slow without conflict. The answer we are usually told lies in the reference frames of specially synchronized clocks which Einstein uses. These clocks, synchronized by back and forth light signals, always record the measured speed of light as the same in all directions. But such clocks also appear out of sync to any observer moving differently due to time dependence on spatial coordinates, or clock skew, or lack of mutual simultaneity as it may be termed. Relativity can easily be viewed without so many extra clocks, but in so doing intuitive notions of simultaneity creep back in and the symmetric mutual effects of time dilation and length contraction begin to seem paradoxical.
Eliminating grids of measuring rods has the same degrading effect on intuition as eliminating the clocks. Without rods filling the empty space of the journey, the applicability of length contraction can be unclear. It is hard to keep a mental model with length, time and simultaneity in mind, and easy to focus on just two observers who see apparently contradictory things. And then there are the points of view of each twin. Even the two views are not sufficient, as we shall see that a 3rd viewpoint adds insight to the turnaround. Like a magic act, the formulation of the puzzle diverts attention onto one aspect, in this case time dilation of the twins themselves, from which the whole trick cannot be easily seen.
This paper will be restricted to the standard twins problem in flat space-time. It will not consider twins in intersecting orbits, in closed space-times, and so forth since the present focus is on the pedagogy of SR. “Trick” papers such as one by Abramowicz (2009) [1] who arranges for the accelerated twin to be older by placing the stay at home twin in a gravitational orbit which also dilates time will not be addressed either. To provide a finite but diverse scope, Einstein’s 1905 and 1918 treatments will be analyzed, along with 21 papers from the American Journal of Physics (AJP), and a paper analyzing how twin students, one with conventional and one with more contemporary tutorial-visual training, work together to analyze the twins paradox.
2. Leading Clocks Lag
The phrases “time dilation” and “length contraction” are easily remembered and convey an immediate sense of the character of observations involving relative motion. But the third essential aspect of the Lorentz transform has no such shorthand expression. In this paper when referring to the skew of clocks in another reference frame with respect to its direction of relative motion, the phrase leading clocks lag will be used. While this is apparent from the negative sign on the x term of the Lorentz transform, recall that it also depends on velocity sign conventions and the reverse transform therefore switches sign, so when students are learning many new things it is easy to become confused.
The principle of relativity requires that all clocks behave the same under transformation, and the Einstein synchronization process itself is a kind of clock, so we may use light clocks as Einstein often did to understand that leading clocks lag. This treatment is not as common as it used to be, so let us consider an example. On one hand it is not obvious to students nor to the public why all clocks (e.g. biological clocks) must agree with the light clock. On the other hand, one of the most striking results of SR is the equivalence of matter and energy, specifically the ability to convert between matter and electromagnetic energy, and in view of that it is at least unsurprising that all material clocks agree with light clocks.
The clocks drawn within the spaceship in Figure 3 are synchronized as viewed by observer B. Clocks drawn below the ship show observer A’s view of the same clocks. Lines a, b and c show the position with respect to A of mirrors 1 and 2 at the time that a pulse of light strikes mirror 1, then mirror 2, and then mirror 1 again respectively. We may imagine there is also a sensor in the mirrors to compare pulse arrivals with the clocks, and some active optical system for regenerating energy lost from the pulse. B sees the clocks make 1/2 revolution for one round trip of a pulse. The clocks are shown pointing straight up at time ta when a pulse leaves mirror 1. Ghost clocks on the right show clock readings of 1/4 for pulse arrival at mirror 2, and 1/2 for arrival back at mirror 1. No ghost clocks are shown for mirror 1 but they would be identical.
Observer A sees a shorter distance between the mirrors due to length contraction, but a longer overall light path because of the relative motion of B. Some older textbooks will show a transverse light clock and light path with a triangular derivation of the Lorentz gamma factor using the Pythagorean Theorem. In that case, the light path is longer by the factor γ = 1/(1 − v2/c2)1/2. Since by assumption all clocks behave alike and the speed of light is constant in all directions, the length of the longitudinal light path in Figure 3 must also be longer by γ in A’s view. Since clock intervals are also lengthened (dilated) by γ the observer A easily explains how B arrives at the same value for the speed of light: light travels farther and B’s clocks tick slower by the same factor.
Next we deal with how B and A describe the synchronization events. B will have the clocks transmit their readings to one another using the light pulse, and will set the clock at each mirror based on the transmitted value plus 1/2 the round trip light transit time. The following explains the time skew in a nutshell:
• For A the time for the light pulse to go from mirror 1 to 2 is longer than the return.
• In order for A and B to agree what clock 2 reads when the pulse arrives (and they must since it is a physical event at a point), the clock at mirror 2 must be set back or lagged as viewed by A in order to allow the extra time for transit from mirror 1 to 2.
Figure 3 also illustrates the connection of simultaneity and relativistic aberration. In the spaceship, two photons are shown as squiggly lines, with a point of constant phase diagrammed as a horizontal double-dotted line. In the view of the same two clocks seen by A below, at the lagging clock the point of constant phase hasn’t arrived yet, so the wave front is tilted. If the speed of light were subject to vector addition as a normal velocity,
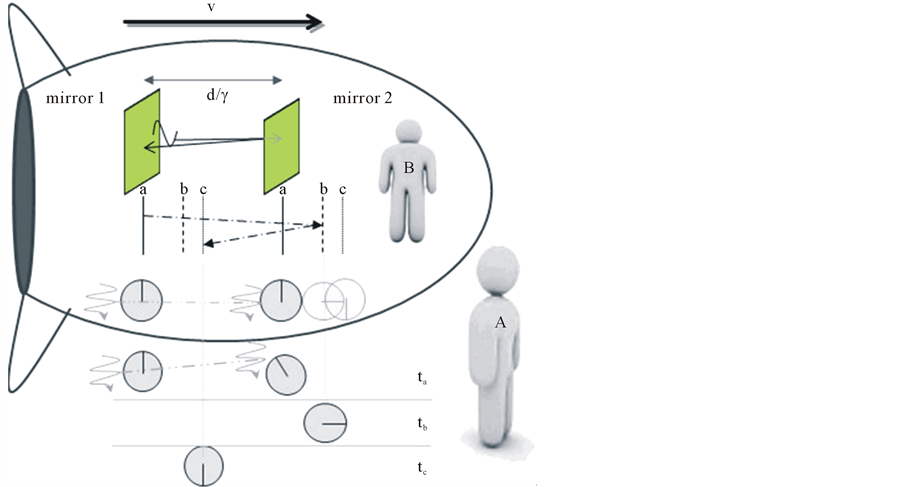
Figure 3. Using back and forth path of light to sync clocks implies leading clocks lag.
then this wouldn’t happen, but the relative speed of the wave would have to be different for each moving observer. Since each observer measures the same speed of light, then the direction of light must appear to change, which is aberration.
3. Einstein’s 1905 Analysis
In his 1905 paper introducing Special Relativity, then called “On the Electrodynamics of Moving Bodies” [2] Einstein describes half the twins problem: “If at the points A and B of the [coordinate system] K there are stationary clocks which, viewed in the stationary system are synchronous; and if the clock A is moved with velocity V along the line AB to B, then on its arrival at B, the two clocks no longer synchronize, but the clock moved from A to B lags behind the other which remained at B by (1/2) (t v2/c2) (up to magnitudes of fourth and higher order), t being the time occupied in the journey from A to B”.
In Figure 4 I have added two things to a diagram of Einstein’s statement. The first is a rod of length L also stationary in K, measuring the distance between A and B at the start. The second is the notation t' for the elapsed time reading of the moved clock. This is given as a negative delta approximation in the quote. The exact expression follows, where γ is the Lorentz gamma factor:
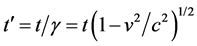
This computation is in the rest frame K, that is to say from the point of view of B, and Einstein does not attempt to give the point of view of A. He chooses to “invoke the 5th” so to speak with regard to applying SR to an accelerated body, even though he does so on many other occasions.
Of those papers on the twins which restrict themselves to SR, there seem to be three approaches:
1) Argument that the viewpoint of the A clock is out of scope and must be treated with GR.
2) Argument from the view of an inertial reference frame similar to the A clock’s, such as a co-moving observer. These are correct within SR’s assumptions and produce the correct answer, but tend to convince the student, including intelligent adult scientists and engineers inquiring into SR, that the theory is hopelessly muddled.
3) Argument using a non-clock technique such as Doppler or parallax, which also give the correct answer yet mostly avoid the student’s real question about mutual relative time dilation.
The papers tend to concern themselves with one of the following:
• Supplying the missing calculation from the traveling clock (or twin’s) viewpoint either by reference frame switching, by equivalence, or by length contraction.
• Calculating how the traveling twin can reconcile apparent time dilation of other twin’s clock with the final result using either reference frame switching (which just moves the mystery around), by equivalence, or by using a signal observer (e.g. Doppler or radar methods, which again just move the mystery around).
• Setting up a tricky situation in which either it is hard to tell who is accelerated, or the un-accelerated twin ages more.
In my opinion, and in the opinion of most students, all these approaches fail on the real objective of providing some insight into relativistic symmetry. But the problem with the educated public is more serious. The public, including medical doctors who are cited in the papers from time to time, want to know by what mechanism it is known that biological clocks progress the same as light clocks, and exactly why the one clock “really” slows
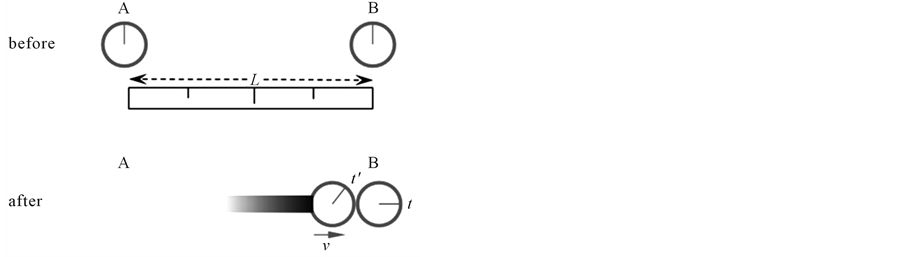
Figure 4. From Einstein 1905, the return voyage only.
down and not the other. Notice that papers on the twins never attempt to answer the two questions interesting to the public, and for this reason alone I suspect we’ll continue to have pedagogical problems and more papers on the twins for some time to come.
4. Cross-Frame Time Seen by a Point Observer
I would like to make two comments on the Einstein 1905 version of the problem. First, consider that time observations, without relying on signaling, are of one of two types. In one of the reference frames at least two clocks are required. For an Einstein observer, two or more clocks record the time of a single moving clock as it passes. This is a 2 on 1 type of measurement, and it results in the observation that the moving clock is slow.
A second completely logical way for a traveler who is a point observer to measure time in another reference frame is to observe and record the other clocks as he passes. This is the 1 on 2 method. Using this method, an air traveler on Earth flying west sees time dilation until crossing the International Date Line, and a traveler flying west sees time compression because of the sun-centric clock synchronization method used by our civilization. Immediately the reader will object that no actual time dilation of individual clocks is detectable this way and of course that is true. But it is a very useful method for predicting arrival times, and understood intuitively by most people.
By the 1 on 2 method, the observer directly views time as defined by occupants of the other frame, not the progression of a single clock. But this time has the interesting property that at any moment the observer chooses to leave her own frame and enter the other (by accelerating appropriately), this is the time that would immediately become “real time” for the frame changing observer. All clocks in this frame would already be synchronized, ready to make relativistic observations and calculations.
An observer A in Figure 5 believes her clocks to be in sync, and makes a comparison of her time to the one clock of observer B in the space ship as it passes each of A’s clocks. The two observers must agree on each observation because each is made with two clocks in the same place at the same time. It is an entirely local physical fact. Therefore B’s reading must reflect the reverse of A’s, and B sees time passing faster for the other frame by the factor γ.
How is this possible? For B, the A frame is moving to the right, and the leading clocks are on the right. B encounters them first. In relative motion the leading clocks of the other frame are always encountered first, and since leading clocks lag, B sees the ticking progress of individual clocks added to the progression of successively less-lagging clocks, just like a traveler flying east. Of course, if B uses two clocks and A one clock, the reverse observation is made and the puzzle returns. But that is only because the clocks have been switched. With the same clocks the measurement will be classically consistent, because if the clocks are not switched there is no possibility to rearrange simultaneity.
5. How to Tell When Empty Space Contracts
My second comment on the Einstein 1905 analysis relates to the use of length contraction to compute the time of

Figure 5. Observing synchronized passing clocks.
the traveling twin’s journey, common at the student level although discussed in only a few papers. As long as there is empty space between the endpoints of the trip, this seems just as ambiguous a determinant as acceleration. But if one imagines an actual measuring rod or tape, or perhaps a series of space stations maintaining their position using radio links, then suddenly it is clear who accelerates. Only the one who lets go of the rod and moves along it can be said to accelerate. There are four considerations:
1) If a measuring rod could have been connecting two objects before one of them accelerated, then it is safe to use length contraction in its simple form.
2) Only the objects which change reference frames (accelerate) see a length contraction of the empty space between objects (where there could have been a physical rod). For the non-accelerated object, this rod remains stationary and does not contract.
3) In the case of distances great enough to encompass expanding space, as for example distances to receding galaxies, GR should be used.
4) In the case of any gravitational fields unequally applied to the twins, gravitational time dilation is an additional factor in computing the time length of that twin’s path. For example, if a twin turns around using a hyperbolic trajectory past a dense object, his clock is slowed by the gravity of that object during the maneuver in addition to the normal time difference in the twins analysis.
6. Swann’s Principle & The Action Principle
The first of two related principles comes from a two part paper by Swann, one of the best papers ever written on the twins though it only gives a partial exposition of the traveler’s viewpoint. Swann devotes an entire paper just to discussing fundamentals about reference frames and clocks [3] and makes the point that the “other” reference frame which we see as moving must have either been constructed from materials already moving with it, and the clocks and measurement instruments synchronized appropriately, or if a system originally built in our reference frame is accelerated, and is made of conventional instruments, it must be re-synchronized after acceleration (unless it is accelerated infinitely slowly). I call this Swann’s clock re-synchronization principle. No law of physics automatically resets classical (large) clocks. Swann assumes, and I agree, that quantum systems synchronize themselves. For that reason, the length of material objects must return to proper proportions after acceleration is ended provided there is no inelastic deformation. But I would add that if the physical dimensions are established with other methods, laser surveying instruments for example, then the physical dimensions as well as the clocks should be recalibrated and synchronized. Students are often given a lecture about Minkowski space which they interpret, even if the professor doesn’t, as implying that these adjustments are not needed.
The point Swann makes in his second paper [4] is that it is not what the traveling twin does with respect to the stay at home. The letters are reversed in Swann’s paper so that it is B who travels. Swann says it is what B does to B in B’s reference frame that causes the time change. And it is assuredly not what B does to A, as at the turnaround B is remote from A and they have no effect on each other at all.
A second related principle is more widely known. In a 2003 guest editorial in AJP, Edwin Taylor discusses how physics is in some places being taught using three (equivalent) action principles [5] . The Newtonian principle of Least Action, Taylor points out, is equivalent to the relativistic principle of Maximal Aging. However, this principle sometimes leads both expositors and students to conclude that the aging takes place during the acceleration, which they not-quite-correctly associate with the “action”. Taylor reminds readers that action is an integral along a path. Brief acceleration can be mostly un-done, leaving opportunity for the other twin to instead take “action” within his own reference frame and become the one least aged when they are re-united.
7. Einstein’s 1918 Analysis
In 1918 Einstein considered the problem of the twins as it had by then been formulated, with B as the traveling twin. He said he could not think of a way to distinguish the relative motions of A and B, and gave an analysis using a brief uniform gravitational field over the entire universe during B’s reversal [6] . Einstein had been thinking about the problem at least since 1911, and had included it in his lectures in 1914.
In using a GR or equivalence solution, Einstein dismissed the standard arguments about the resetting of clocks and Minkowski space which had by then appeared and still so frequently appear in one form or another. Perhaps he didn’t like clocks jumping around at a distance, and the implication that it was this effect that “caused” the stay-at-home twin to age more. Later he objected to “spooky action at a distance” in quantum entanglement.
Figure 6 shows A and B and an array of synchronized clocks in A’s reference frame before and after the turnaround maneuver. Clocks near the spaceship would be affected the same as the spaceship during the turnaround, and all would run very slowly due to the low gravitational potential. Clocks higher in the pseudo-gravity field, farther “up” in the direction of acceleration (or to the left in the figure), would run faster. The correct answer is easily obtained this way, and not surprisingly because Einstein based his gravity theory on the equivalence of gravity and acceleration.
In developing GR Einstein carefully confined equivalence to an infinitesimally small laboratory. In the twins problem, under pressure to resolve a criticism of relativity that was mounting and spilling over into the popular press, he extended equivalence and apparently, or so it seems, overlooked the effect on the synchronized clocks of A’s reference frame. They are all driven at different rates by the gravitational field, and this is an absolute not a relative effect. Synchronization cannot be maintained for clocks at different heights in a gravitational field. The two particular clocks mentioned in the problem, which are in different frames, obtain the correct settings but most other clocks in the universe would be wrong. This was mentioned in 2005 by Unnikrishnan [7] . Other authors have just pointed out that a GR solution is misleading, or that it only proves GR has been formulated correctly. The clocks could eventually be fixed by applying equal and opposite accelerations. But during travel other observers would notice their clocks out of synchronization.
8. Classifying the Literature
Now we investigate viewpoints and methods given in subsequent literature, with particular attention to how these may have changed over time. Since the largest plurality of articles was published in the American Journal of Physics, and since that publication is concerned with the teaching of physics, those articles were selected as a representative sample. A search was performed on Google Scholar for articles mentioning “twins”, “paradox”, and “American Journal of Physics”. This produced 400 hits, all of which were examined. Many were citations. Twenty one direct articles in AJP were identified as relevant for analysis. This does not seem to include every article, but it is just a device for selecting a representative sample. The choice of keywords, omitting “clock”, deliberately excludes older papers from the first half of the 20th century when that terminology was more prevalent. Papers treating non-flat space-times were also excluded.
Table 1 summarizes the articles. Papers treating the problem essentially as in Einstein’s 1918 analysis appeared in 1957, 1979 and 2007. The 1959 paper by Scott has 4 methods, and while Scott maintains the GR method is not necessary, he includes it. R. Muller in 1972 takes the same position that GR can be used but is not necessary. Except for one later case where the GR treatment is again included along with both reference frame and length contraction treatments, its use in connection with the twins problem could be said to be diminishing.
There can be said to be four questions in the puzzle of the twins. If we take A as the stay at home twin and B
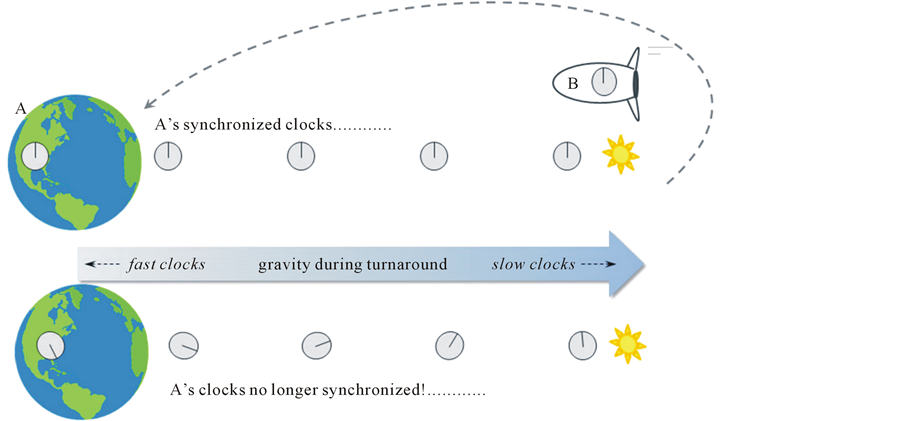
Figure 6. Equivalence (pseudo-gravity) solution.
Table 1. AJP articles directly treating twin clocks problem.
as the traveler, then: 1) A’s view of the time on A’s clock and 2) on B’s clock, and B’s view of the time on 3) B’s clock and 4) A’s clock.
9. Examples of Student Difficulties
When reviewing this literature it is useful to have in mind some problems actually encountered by students. Cormier and Steinberg interviewed identical twin brothers working together to solve the twin paradox, both “intelligent and articulate science students, with similar… undergraduate backgrounds [28] ”. The twins differed in that one of them, whom the authors call “Fred”, had taken a newer tutorial based curriculum. The results express clearly the points of relative difficulty in visualizing and solving the twins problem.
Both twins easily answered as to A’s view of A’s clock and A’s view of B’s clock. There was no problem calculating in the original inertial frame. The problems began when switching frames. Fred, with the newer curriculum, was uncomfortable using length contraction to calculate a shorter trip time on B’s clock, but George was able to persuade him after some discussion. So length contraction is a key calculation tool for one of the important answers, but is weakly understood and accepted, more so in newer educational curricula.
As to the question that resolves the “paradox”, the question of how B views A’s clock, the twins both failed to get a right answer. This analysis must consider that B switches frames at least twice, and during the second switch, the turnaround, does not have a first-hand view of A’s clock. For this question Fred, who had the tutorial approach, seemed (correctly) concerned that it was illogical to have two different answers for A’s clock at the end, one perceived by A and one by B. The tutorials seem to have been of benefit, but not enough to overcome George’s conviction that differences in observation were simply allowed because “That’s what relativity is”.
10. Traditional Approaches
The classification of “frame switch” in the table above designates papers that highlight the mathematics of the frame switch at the turnaround, and which use the basic Lorentz transform, Minkowski space, or a concept derived directly from those. This method is mathematically correct, is a good way to go about solving the problem, and contains a spooky time jump that is extremely difficult to visualize or understand. It is this problem which inspires the vast majority of papers.
Some commentators would say that no progress has been made. In 1996 Debs reaches this conclusion, and quotes from earlier authors that said the same thing in their own era. But the record seems to be that while some misinterpretations were made early on and repeated, gradually they have been corrected.
First if one looks at “where” various authors indicate the time difference accrues, from 1957 to 1981 five out of eight papers either stated or left the impression that this occurs during the turnaround. These include two of the gravity or equivalence based papers already mentioned, and one each of papers using the frame switch, Doppler and parallax methods. But thereafter many “rebuttal” papers appear. The case for a gradual change in the perception of the problem gets even stronger if we look also at whether the change in clocks was attributed to acceleration directly, as for example during the turnaround, or to something else, generally to the travel portion of the trip. Acceleration itself falls out of favor after 1980. Boughn in 1989 examines a case of identically accelerated twins which age differently. Gruber in 1997 devotes the main topic of his paper to arguing against aging occurring during acceleration. Acceleration comes to be correctly seen as an instigator of something which then accumulates over an interval of travel. But without the interval of travel, there would be no differential aging.
Only a few of these papers are aimed at students (e.g. Boughn). Most of the later ones are aimed at physicists, and there is even some grumbling about the level of abstraction, as for example Gruber complains regarding Debs’ treatise on the conventionality of simultaneity, “While this is quite interesting in connection with the logical structure of special relativity, it is of little value to the student encountering the twin paradox for the first time”.
The “conventionality of simultaneity” refers to the means of synchronizing clocks, which is usually to communicate the settings of one clock to another and to adjust the second clock using half the two-way light transmission time. This was the Einstein convention. It is also the convention that obtains if clocks are moved apart infinitely slowly as pointed out by Price in 1996 and other authors as well. In that case no Swan re-synchronization is needed. With these two papers, the formal literature on the twins catches up with what every student is taught, that long distance simultaneity is disagreed upon by different observers, and therefore not particularly meaningful. Swann was also saying this in 1960 but others were still trying to pin it down at that time. After the two 1996 papers we see less attempt in the literature to pin down where or when the clock difference accumulates. Indeed, if B did not turn around, and A decided to accelerate and catch B, then A would be the younger. So just before B turns around, it is indeed not possible to say who will in the final analysis be younger, much less where it occurred.
If a different point other than 1/2 the two-way light travel time is used for synchronization, this is what Debs and Redhead mean by “convention of simultaneity”. Referring to the figure on synchronizing clocks using light above, one can see that choosing a value other than 1/2 is a lot like viewing the synchronization process from another reference frame. In that sense, each time any of the paper authors switches one of the twins into a different co-moving reference frame (as many of them do), a different convention of simultaneity is adopted. It is connected to relative velocity when done in this way. But one can disconnect it if one wishes by only briefly switching to the co-moving frame, or “consulting” the co-moving frame to make measurements. So it seems that what Debs and Redhead have really done is to codify the range of possibilities from every accessible co-moving frame, to create a range of possible outcomes which is, logically enough, proportional exactly to the light travel time between two observers, and decreases as the observers are brought together. This is the point of “interest” which Gruber doubts will much help first time students of SR. Perhaps the abstraction level of Debs and Redhead is a bit high, but unless students understand what outcomes are not settled they will be easily tripped with so-called “paradoxes”.
11. Educational, Tutorial and Visual Approaches
Attempts at parallax and radar time are interesting and the author himself has spent much time developing and using similar methods. But from personal experience, these methods, designed to be explanatory, are more often greeted by blank looks than by the “ah ha” of comprehension. The final paper by A. Müller is not concerned with finding abstract answers, but with creating simulations of what the star field looks like as journey at higher and higher velocity is actually made. All of the signal observer based papers in one way or another do this and the signal observer model has definitely been a trend since Unruh in 1981.
The “new” educational methods referred to by Cormier and Steinberg included Tutorials in Introductory Physics [29] , parts of which are described by Scherr, Shaffer and Vokos of the University of Washington Physics Education Group [30] . Recall that “Fred” in Cormier and Steinberg’s interview had used this material while “George” relied more on solving end of chapter problems and other traditional methods. Of course the interview of two students is not statistically significant, but it is an intriguing talking point because Fred and George were in fact identical twins with non-identical physics education. The example in the paper by Scherr et al. is Einstein’s moving train thought experiment in which a signal flashes simultaneously at the front and back in ground observer A’s frame, and an observer B stands at the middle of the train. This is a long way from the twins problem. It is designed only to illustrate simultaneity changes and as used in Scherr’s paper length contraction is not addressed, which possibly suggests why Fred was hesitant to use it.
The train thought experiment is very old, but it seems similar to the new trend in twins papers which use signaling approaches such as optical, Doppler, parallax or radar. In all these cases point observers receive signals. They do not use reference frame grids with synchronized clocks. The modern papers are certainly superior to the train as a representation of the twins problem since they use repeated signals, so that not only arrival times but rates are used. The rates don’t obviously correspond to Einstein 2 on 1 clock observations however. In fact by the end of the trip they have in aggregate corresponded to a 1 on 2 measurement as any solution must (the traveling twin encounters A’s origin clock twice). Note that if the single ground observer A in the train experiment were to record the readings of the passengers watches as they passed, he would certainly conclude time on the train was running faster because this is a 1 on 2 measurement.
It is interesting to note another popular modern explanation, which is in the form of informal educational material for adults and not a technical paper and so not listed in our table, but is delivered in video as a lecture by Neil Tyson from one of The Great Courses, and can be viewed online at http://www.youtube.com/watch?v=n2s1-RHuljo. Dr. Tyson does a better job than most of explaining time dilation, which he says is not just the slow running of clocks but all processes, including synapse activity, and so one never notices that her own time has been slowed. But he introduces a hint of trouble by treating motion and gravitational time dilation with one broad brush. Then when explaining the twin paradox, Dr. Tyson never discusses how the traveling twin might think the Earth twin should have been younger. He only says that it used to be called a paradox because the idea of twins aging at different rates does not fit the classical picture of time. Taken together with the newer papers on radar, Doppler and visualization of star fields, there does seem to be a trend to avoid the knottier aspects of the problem.
12. Constructive Approaches
That leaves two interesting papers we have not in one way or another discussed. One is a circular version of the paradox, not in curved space-time but rather a series of observers spread along the periphery of a rotating disk as described by Cranor, Heider and Price. Their conclusion is that if these observers follow an Einstein synchronization method in one direction along the periphery, when the process comes around again to the first clock there will be an irreconcilable time gap. It is a shame that the authors do not connect this with the Ehrenfest paradox regarding a spinning cylinder or disk. This was put forward by Paul Ehrenfest in 1909 and a variation used in the development of GR by Einstein. There are two takes on the disk. One is that since measuring rods will be contracted, more of them will fit along the circumference. The other is that if the disk perimeter itself contracts, the disk must break. The latter is basically a circular version of Bell’s Spaceship paradox. Here we see the symmetry between time synchronization and length contraction. One goes with the other. Another interesting aspect of the circular twins problem is that by bringing the traveling twin repeatedly back to the starting point, symmetric relative time dilation is repeatedly converted to actual time dilation of the moving twin.
Only one paper is concerned with explanations of relativistic effects, the one by Bohm in 1985 which is entirely concerned with them but is not specific. One could also possibly say the one by Swann is explanatory in regard to synchronization of clocks, and the equivalence (GR) based papers which could be said in some sense to be explanatory. What Bohm describes as an “active” interpretation of the Lorentz boost seems to be the same thing that Einstein and others up until the current day call a constructive approach to SR, as opposed to a principle approach. In the principle approach, the axioms are introduced and the algebra of the Lorentz transform is worked out in a page or two. The abstraction level is very high, but if one is convinced of the power of mathematical deduction the results must be accepted. In addition to Bohm, there are papers appearing elsewhere up to the current time advocating the constructive approach for teaching. John Bell was noted for advocating such an approach [31] .
On the one hand, it seems like a constructive approach would be more intuitive, and indeed the author’s own learning of SR included some 20 pages of discussion of light clocks and other simple constructivist treatments by R. H. Good [32] in a delightful 1968 book, now out of print, before the Lorentz transform was formally derived. On the other hand, every paper the author has found on constructivist pedagogy does not live up to its promise, and gets lost in incomplete derivations involving usually Maxwell’s equations. Bohm just makes suggestions, not derivations, but since the end result is identically the phenomenology described in the other 20 papers (Bohm even briefly refers to the gravity explanation, among others) without making a concrete suggestion about how the active boost mechanism works, it is not clear to me how it would be clear to students. However, I felt the Cranor, Heider and Price paper on a circular twins paradox was interesting and in the category “constructive” since it called out various algorithms for synchronizing clocks, including the Einstein procedure applied in a specific order around the disk.
13. A Trailing Twin’s View of the Turnaround
There is a way to diagram what happens during the turnaround that is more concrete than space-time diagrams, without getting bogged down in constructivist theories. First note that one of the most useful tools for students is to actually visualize, or draw, clock grids wherever we normally say “reference frame”. Swann and Price use something similar to this, having for example an A-frame observer at the turnaround point, or having an outbound B-frame observer continue past the turnaround point.
Having an A-frame clock at the turnaround allows B to see what A’s clock reads according to the A-frame. As we saw earlier, having A-frame clocks available all along the way would help B to visualize that time is passing faster in A’s reference frame. Note that if A never changes reference frames, and B and A get back together, this perception of time becomes true. (If A moves to another point in the A-frame, that requires two frame changes for A).
Now imagine clocks trailing along behind B in the B-frame, physical clocks, which synchronize their time and their separation using light signals. This frame is not only real and constructivist (without resort to any particular theory of rigid matter), but we could construct one. For local voyages we have constructed one. It is called the Global Positioning System. By various transmissions and corrections, GPS allows virtual clocks in the frame of the earth to be materialized at any point surrounding the earth by any device with a radio receiver and the correct algorithm. (In fact the GPS timing accuracy even with receiver flaws is of the order of 100 nanoseconds, 1000 time less than the SR time skew at a point half way around the Earth for an observer moving with equatorial velocity).
In the top of Figure 7 labeled “1” we see the outbound journey in the B reference frame at the moment B reaches the destination. All of B’s clocks have the same reading. B sees the A-frame as moving to the left, so the clock at A is the most leading and therefore the most lagging, and for B none of the A clocks seem to be in sync.
Let B stop at the destination long enough to re-synchronize the B frame, shown in the middle part labeled “2”. Rarely mentioned in the twins literature, half way through the turnaround B sees the distance to the starting point restored to its rest length. In other words, not only do clocks appear to jump around, so do planets.
Suppose there is a third twin, or triplet or sibling, trailing along at the position of clock B4 which was near the starting point at the beginning of B’s turnaround. This twin is not near the starting point when B pauses half way through the turnaround! B does not keep a consistent clock near the starting point to reliably observe, without
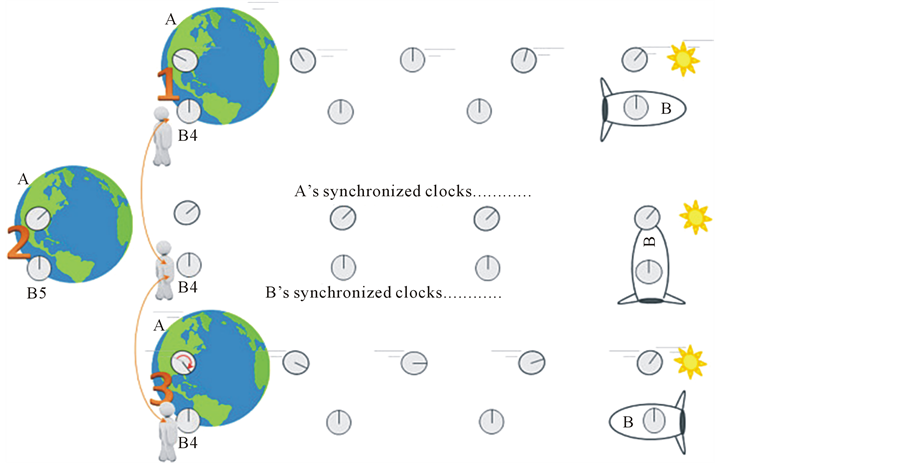
Figure 7. Frames co-moving with B before turnaround (1), paused (2), and after (3).
simultaneity disruptions, what is going on at the starting point during the turnaround.
The illustration of the trailing twin seems to suggest he sees Earth fly away backward which the Earth does not do, so in the spirit of relative motion the trailing twin continues forward past the moment of turnaround in the original right moving B-frame, but as part of the re-synchronization process not as a continuation of the original motion. The details of re-synchronization we have not specified, so we will not attempt to clarify this motion.
In part “3” when B completes the turn, the B-frame looks unchanged from part “1” but now the leading clocks in the A-frame are the ones near the destination, and the puzzling time gap at A appears, shown by the little arrow on A’s clock. The trailing twin reappears at the simultaneous moment of B’s completion of the turnaround, in time to observe the new value of A’s now advanced clock.
What happens during the turnaround is not that A’s clocks get adjusted, but as Swann said, B does something to B! The author hopes this visualization will help some student somewhere understand that observationally both the clock and the time used by B have changed, because of the necessity of adjusting B’s clocks and their spacing. From this the author concludes that Swann’s principle applies to both clocks and lengths.
Now suppose that A and B are physics teachers who wish to conduct a demonstration to clear up what happens at the starting point during the turnaround. Each clock is fitted with a computer and a propulsion system, and the trailing twin at the B4 clock decides to just stop when he reaches the starting point, and stay there until the time at which he would be passing the starting point going in the other direction. This will allow the trailing twin (B4) to observe what happens at A during the turnaround, and we show this with the same three parts in Figure 8.
In part “1” the B4 trailing twin arrives, thinking B is beginning the turnaround. The B4 clock exchanges messages with A and discovers that in A’s frame, B has not yet reached the turnaround. In A’s frame, B’s space ship clock is leading and thus lags B’s number 4 clock, so the arrival of B4 at A, and B’s arrival at the destination, are not simultaneous in A’s frame. There is an uncertainty, or meaninglessness, of simultaneity at a location remote from observers.
So the B4 clock just waits for B to arrive at the destination and begin turning around. Half way through the interval the B5 clock arrives and reverses direction. Finally in part “3” when B is well on his way back, it is time for B4 to at last reverse direction and head back to the left. The “jump ahead” interval in the A-frame did not entirely occur while B was turning around, but also while B was finishing the voyage and heading part way back. It is a matter of changing views of simultaneity. From B’s point of view, there is simply a gap in knowledge of what happened at the starting point. From A and B4’s point of view, all of A’s clocks were ticking together, including the one at the destination. But B is not even at the destination most of that time.
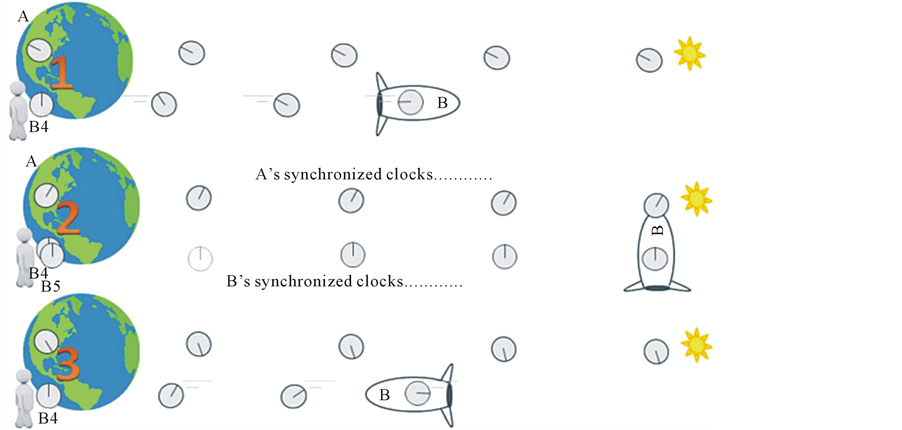
Figure 8. Same three events with clock B4 pausing in A’s reference frame.
At the end of the experiment, how much time has elapsed on the trailing twin’s clock?
Notice that the question does not ask whether the trailing twin is older or younger because this twin is not at the same position as the others in the end and so the question lacks meaning. The clock reading has objective meaning only within a consistent reference frame. B4 was co-moving with B for most of the return journey, again depending on the point of view, and was synchronized, so using this frame for the final leg of B4’s three part journey we see that B4’s clock at the end, though remote, reads the same as A’s. This is because B4 lived in A’s reference frame during the time jump while B was turning around, and otherwise followed B’s clock. But had B4 not paused at A the reading would still be the same, as we exactly reconstructed the clock readings of Figure 7 and Figure 8.
14. Questions about Simultaneity and Speed Limits
Even after the procedures for analyzing the twins are well in hand, two problems may bother students or anyone. One of them has to do with nagging notions about simultaneity and may show up as a question like “I know we can’t have instant communication, but if we did what would we find?” This is an actual question the author was asked. We would of course find a preferred reference frame. Nothing else would change. Physicists, including Lorentz, did not want a theory that contained something they couldn’t detect, so they chose SR over Lorentzian Relativity (LR). If such a thing as faster-than-light communication was discovered against all odds and expectations, then all other reference frames would be Lorentzian distortions of a preferred frame, and instant communication would not be possible in any of the distorted ones.
Without instant communication in at least two different reference frames, there is no way to send a message that arrives before it is sent, and thus no time travel paradoxes in either SR or LR. All that happens when only one frame allows instant communications is that observers moving with Lorentz relativity to that frame can exchange messages with space-time points in their reference frames for which simultaneity is ambiguous or meaningless, as shown by Swann and by Debs and Redhead. There is no meaning to saying a message arrived before it was sent, since the arrival was at a distant point for which “before” is undefined. Only by switching frames and sending another super-fast message back to the origin is causality violated. That requires two differently moving frames with simultaneous communication.
The implications of finding shortcuts to communication or travel depend on the mechanism of the shortcut. If by quantum entanglement, then no information is communicated until comparison is made with reference measurements and no preferred frame can be detected, thus there is no disturbance of SR. If by wormholes or Albucurrie warp drive, these are features of GR’s curved space-time requiring negative energy and therefore rather improbable, and have no bearing on SR. If by some sort of faster than light mechanism, then it would only mean finding a preferred frame and adopting the mathematically indistinguishable LR theory. At the present time that seems even less likely to most physicists than finding negative energy. Some twin’s papers published in more speculative journals suggest a reference frame defined by isotropy of the cosmic microwave background. It’s a nice reference frame for viewing the universe, but so far there is no experimental evidence that it is special with regard to the propagation of light or the laws of physics.
15. Why Does One Clock Show Less Time?
Regarding the question of why B’s clock runs slow, if the light clock examples have been used then this question will not refer to physical mechanisms. The light clocks are a mechanism but don’t answer this question since they still have the paradoxical quality of each appearing slow to the other. I suggest following Swann. It is because of what B does to B within B’s reference frame. The Lorentz transform contains a geometric mean of (1 + v/c) and (1 − v/c). A geometric mean of two quantities is the square root of their product. This gives the inverse of the Lorentz factor. The geometric mean is graphically seen in the derivation of the Lorentz factor for transverse light clocks using a triangular light path and the Pythagorean Theorem. But it has subtle implications that might be more obvious to an economist or biologist. A geometric mean of equal deviations about a central value is always less than the central value (“1” in this case). And as the equal deviations (+ and − v/c) increase, the amount by which the central value is reduced becomes dramatic. This is seen, for example, in investment losses due to volatility, especially in risk multiplier investment funds (or ultra-funds).
So the traveling twin, by changing reference frames, imposes a geometric mean on his time accumulation rate. It is not the acceleration itself. If the distance traveled is trivial, then clock differences will be trivial even for large accelerations. It also does not matter whether the velocity change is by conventional acceleration or acceleration-free gravitational (orbital) maneuvers.
16. Is Length Contraction Real?
Obviously the lengths of things (and the rate of clocks for that matter) do not change because they are observed by something flying by, and this might lead the student to suppose that all the relativistic changes are only appearances (as some physicists argued in the early history of SR). Such a conclusion intensifies the mystery of the disagreement of the twins’ clocks when they are reunited. While a careful following of the traditional arguments leads to the correct conclusion, that accelerated lengths change (and in fact must be “adjusted” if not part of a quantum system as per the Swann principle), this question affords the opportunity to illustrate the matter bluntly by several methods.
One method, not original with the author but I cannot find a handy reference for its first use, is to point out that in two frames A and B if B accelerates, only B views changes in A or any other frame, but all frames view changes in B, giving them a different status. All frames do not view the same change in B as it is due in each case to relative motion. Some will view decreasing and some increasing lengths.
In the old Lorentz-FitzGerald ether theory based on Fresnel’s suggestion that objects do not drag the ether along with them, length contraction was supposed to be due to motion through the ether, and Lorentz worked out a detailed theory of the electron using Maxwell’s electromagnetics to account for it. Ever since Einstein’s suggestion of Special Relativity there has been occasional confusion among physicists over whether the SR length contraction is fundamentally different than LR length contraction, and whether SR length contraction was equally real or just a rotated “view” of an object in Minkowski space-time. This gives rise to somewhat deeper student questions about not only length contraction but Minkowski space-time and world tubes. One physics educator and author recently summarized the student question like this: “The two three-dimensional cross-sections of the meter stick’s worldtube nicely explain the effect but is this a true explanation? Is the worldtube of the meter stick a real four-dimensional object? Is spacetime nothing more than a four-dimensional mathematical space or is it a mathematical model of a real four-dimensional world with time entirely given as the fourth dimension?” [33] .
At first one might label the question as merely philosophical, but the same educator who phrased the above question complains that it has not been addressed by physicists and gives an example of where it might make a physical difference: “For example, the temptation to interpret the relativistic length contraction in terms of deformation forces is sometimes difficult to resist despite the fact that the muon experiment, for instance, completely ruled out such an interpretation by demonstrating that space itself (where there are obviously no deformation forces) contracts relativistically as well”.
It is possible to make arguments about forces similar to those of Lorentz but in a purely relativistic way, and this is what Bell does in his essay on teaching which we already mentioned. In the same essay he devises the Bell Spaceship paradox to demonstrate the reality of length contraction and the physical deformation of accelerated objects. In fact physical stresses in SR were suggested at least as early as 1959 by Dewan [34] . The presence of such stresses would seem to coincide with Swann’s notion of quantum mechanical systems adjusting themselves. Otherwise, objects not coupled in a quantum system require some adjustment after acceleration as we saw in the discussion of Swann’s principle, and this applies to clock synchronization and spacing (length).
It is difficult to decide what is a matter of fact and what is a matter of interpretation, as virtually all physicists get the same answer to any given problem statement. For example some carefully choose arguments to portray Bell’s spaceship problem as not a matter of length contraction and suggest that in Bell’s argument about forces only material objects could be contracted, not space [35] . But according to Swann’s principle, accelerating collections of objects with spatial gaps (of which Bell’s two spaceships are an example) must make adjustments to clocks and positions to become again a qualified Einstein reference frame. After the adjustments, the empty spatial distance would have changed. The force required to make the adjustments is analogous to the stresses supposed by Dewan. Dieks’s shows that the existence of stresses or dynamical explanations of the Lorentz contraction do not imply an ether and are valid in either LR or SR [36] . Rather than attempting to resolve the issue, the author suggests that discussion is appropriate for more advanced students who may go on some day to formulate theories on matters such as quantum gravity and will themselves have to make decisions about whether to take a constructive or principled approach, or something in between.
17. Conclusions
The twin paradox in light of this paper is seen not to be just a problem for students (though it is that). It shows clearly all the main features of Special Relativity. We have shown primarily a fresh point of view of what happens during the turnaround from the point of view of one of B’s clocks which happens to be at the starting point at the moment of simultaneity in B’s outgoing frame when the turnaround begins, and remains there until the moment of simultaneity of the end of the turnaround in B’s returning reference frame. This point of view is essentially in the stay-at-home twin’s reference frame for the interval, and what it observes instead of just the turnaround, is the end portion of B’s journey to the destination, the turnaround, and the early portion of B’s return. This is due to shifting views of simultaneity. We have also attempted to put the visualization of simultaneity on a stronger footing, more comparable to time dilation and length contraction, by introducing the notion of leading clocks lag with light clock and wave front models.
Also some misleading aspects of earlier solutions were clarified, and trends of publication volume and content were analyzed, suggesting increasing rather than decreasing interest in discussing the twins and a tendency to favor visualizable approaches and single observer approaches. The author hopes to have moved the simultaneity problem a little closer to being “visualizable”, and to have provided some rational approaches to answering esoteric student questions by encouraging rather than dismissing student curiosity and critical thinking.
References
- Abramowicz, M.A. and Bajtlik, S. (2009) Adding to the Paradox: The Accelerated Twin Is Older. arXiv:0905.2428 http://arxiv.org/abs/0905.2428
- Einstein, A. (1905) Annalen der Physik, 322, 891-921. https://www.fourmilab.ch/etexts/einstein/specrel/www/
- Swann, W.F.G. (1960) American Journal of Physics, 28, 55.http://scitation.aip.org/content/aapt/journal/ajp/28/1/10.1119/1.1934976
- Swann, W.F.G. (1960) American Journal of Physics, 28, 319-323. http://scitation.aip.org/content/aapt/journal/ajp/28/4/10.1119/1.1935795
- Taylor, E. (2003) American Journal of Physics, 71, 423. http://dx.doi.org/10.1119/1.1555874
- Einstein, A. (2002) The Collected Papers of Albert Einstein, Volume 7: The Berlin Years: Writings, 1918-1921. (English Translation of Selected Texts). Princeton University Press, Princeton.
- Unnikrishnan, C.S. (2005) Current Science, 89, 2009-2015.http://www.iisc.ernet.in/currsci/dec252005/2009.pdf
- Frye, R. and Brigham, V. (1957) American Journal of Physics, 25, 553. http://dx.doi.org/10.1119/1.1934547
- Scott, G. (1959) American Journal of Physics, 27, 580. http://dx.doi.org/10.1119/1.1934918
- Romer, R. (1959) American Journal of Physics, 27, 131. http://dx.doi.org/10.1119/1.1934783
- Muller, R. (1972) American Journal of Physics, 40, 966. http://dx.doi.org/10.1119/1.1986722
- Perrin, R. (1979) American Journal of Physics, 47, 317. http://dx.doi.org/10.1119/1.11835
- Staunton, L. and van Dam, H. (1980) American Journal of Physics, 48, 807. http://dx.doi.org/10.1119/1.12229
- Unruh, W.G. (1981) American Journal of Physics, 49, 589.
- Good, R. (1982) American Journal of Physics, 50, 232. http://dx.doi.org/10.1119/1.12862
- Bohm, D. and Hiley, B. (1985) American Journal of Physics, 53, 720. http://dx.doi.org/10.1119/1.14300
- Blatter, H. and Greber, T. (1988) American Journal of Physics, 56, 333. http://dx.doi.org/10.1119/1.15633
- Boughn, S. (1989) American Journal of Physics, 57, 791. http://dx.doi.org/10.1119/1.15894
- Debs, T. and Redhead, M. (1996) American Journal of Physics, 64, 384. http://dx.doi.org/10.1119/1.18252
- Price, R. and Gruber, R. (1996) American Journal of Physics, 64, 1006. http://dx.doi.org/10.1119/1.18318
- Gruber, R. and Price, R. (1997) American Journal of Physics, 65, 979. http://dx.doi.org/10.1119/1.18700
- Cranor, M., Heider, E. and Price, R. (2000) American Journal of Physics, 68, 1016. http://dx.doi.org/10.1119/1.1286313
- Dolby, C. and Gull, S. (2001) American Journal of Physics, 69, 1257. http://dx.doi.org/10.1119/1.1407254
- Eagle, A. (2005) American Journal of Physics, 73, 976. http://dx.doi.org/10.1119/1.1994855
- Minguzzi, E. (2005) American Journal of Physics, 73, 876. http://dx.doi.org/10.1119/1.1924490
- Styer, D. (2007) American Journal of Physics, 75, 805. http://dx.doi.org/10.1119/1.2733691
- Müller, T., King, A. and Adis, D. (2008) American Journal of Physics, 76, 360. http://dx.doi.org/10.1119/1.2830528
- Cormier, S. and Steinberg, R. (2010) The Physics Teacher, 48, 598. http://dx.doi.org/10.1119/1.3517026
- McDermott, L. and Shaffer, P. (2001) Tutorials in Introductory Physics. Prentice Hall College Div., Upper Saddle River.
- Scherr, R., Shaffer, P. and Vokos, S. (2002) American Journal of Physics, 70, 1238-1248.
- Bell, J.S. (1976) How to Teach Special Relativity. Progress in Scientific Culture, 1, 2. (Reprinted in Bell 1987)http://philpapers.org/rec/BELHTT
- Good, R. (1968) Basic Concepts of Relativity. Reinhold Book Corporation, NY.
- Petkov, V. (2007) Foundations of Physics, 37, 1499-1502. http://dx.doi.org/10.1007/s10701-007-9178-9
- Dewan, E. and Beran, M. (1959) American Journal of Physics, 27, 517-518. http://dx.doi.org/10.1119/1.1996214
- Petkov, V. (2009) Accelerating Spaceships Paradox and Physical Meaning of Length Contraction. arXiv:0903.5128 http://arxiv.org/abs/0903.5128
- Dieks, D. (1984) Foundations of Physics, 15, 330-342. http://dx.doi.org/10.1007/BF01801366.


