Journal of Modern Physics
Vol.5 No.11(2014), Article
ID:47489,4
pages
DOI:10.4236/jmp.2014.511103
Some Possible Particles Decays from pp Collisions at LHC Experiment
Hasan Arslan
Physics Department, Bingöl University, Bingöl, Turkey
Email: hasanarslan46@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()
![]()

Received 29 February 2014; revised 22 April 2014; accepted 14 May 2014
ABSTRACT
Some of the possible decays of pp collisions at LHC experiment are considered. The vector bosons mediating in the electroweak interactions and right-handed leptons except neutrinos are assumed to be the most resultant particles from the pp collisions. Neutrinos and anti-neutrinos will be observed when one-double electron charged vector bosons are the resultant particles. The charge conservation is thought to be the dominant factor of these decays. The amplitude transitions for Feynman diagram of these decays are written.
Keywords:Z' Boson, W' Bosons, Resultant Particles from pp Collisions, Scattering Amplitude

1. Introduction
The Standard Model (SM) is in difficulties with defining the problems:
1) The Higgs particle mass2) Including the gravitational interactions to the SM3) The dark matter representation in the model4) The masses for neutrinos5) Large gap energy between electroweak scale and Planck scale6) The unification of gauge couplings of the electroweak interactions at some energy scale if the four fundamental forces are the result of a local gauge theory with a higher fundamental symmetry.
The recent experiments mainly LHC and the future colliders will solve these problems. The electromagnetic field interactions and weak interactions are combined in a single representation by the Glashow-Weinberg-Salam Model of the electroweak interactions based on the gauge group SU(2) × U(1) which is in good agreement with the experimental results. Later the strong interactions are included to the theory and the group is written as SU(3)C × SU(2)L × U(1)Y. This group defines the SM particles. Since the four fundamental forces; weak, electromagnetic, strong, and gravity; are equal at the Grand Unified Theory (GUT) energy scale, the some of the additional neutral gauge bosons might be discovered at CERN LHC experiment as well as the lightest supersymmetric stable particle of the dark energy and the particles which have at the same time the properties of the leptons and quarks or the states changes to each other named as lepto-quarks or exotic fermions. The fermionic particles of the SM are grouped in the representation of the three generations as
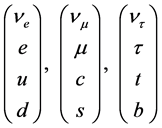 (1)
(1)
The first two particles of each group are the leptons with charges 0, –1 respectively in the unit of the electron charge. The last two are quarks with the electron charge +2/3 and –1/3 for u and d type quarks. Each particles described have their anti-particles. These particles all together build up the matter around us.
2. Some Particles Decaying from pp Collisions at LHC
The breaking of 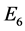 gives other gauge groups. Concentrating on the SU(2)L × U(1)Y × U(1) effective theorythe
gives other gauge groups. Concentrating on the SU(2)L × U(1)Y × U(1) effective theorythe![]() ,
, ![]() ,
, ![]() are the possible U(1)’s in broken E6 GUT’s and the extra U(1) is an Abelian symmetry with its associated “hypercharge” Y [1] ;
are the possible U(1)’s in broken E6 GUT’s and the extra U(1) is an Abelian symmetry with its associated “hypercharge” Y [1] ;
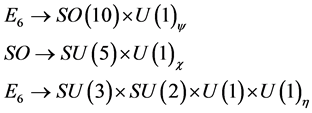 (2)
(2)
The symmetry will be spontaneously broken by a Higgs sector consisting of one doublet and one singlet [1] .
The decays 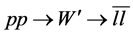 have the same validity as the decays given by
have the same validity as the decays given by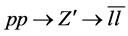 , where
, where 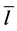 refers to anti-leptons except right-handed neutrinos. This is true because in [2] [3] the mass of the
refers to anti-leptons except right-handed neutrinos. This is true because in [2] [3] the mass of the 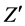 is estimated by calculating the
is estimated by calculating the 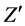 decay width as the same procedure of calculating the
decay width as the same procedure of calculating the 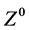 boson decay width. Using the relation [4]
boson decay width. Using the relation [4]
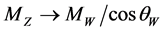 (3)
(3)
given for the 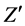 and
and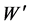 , there is no doubt in writing the relation as
, there is no doubt in writing the relation as
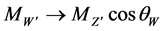 . (4)
. (4)
In [2] [3] 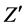 mass is estimated around 630 GeV and the Weinberg angle is taken as
mass is estimated around 630 GeV and the Weinberg angle is taken as
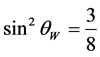 (5)
(5)
at GUT scale. Therefore,
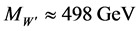 . (6)
. (6)
Using the conservation of the protons’ charges, some of the possible pp collisions decays will be such that (Figure 1 and Figure 2).
When it is assumed that the anti-leptons are the resultant particles as the vector bosons then the right-handed neutrinos couldn’t be seen as the resultant particles. In these decays instead of the intermediate vector bosons the neutral and plus-charged Higgs bosons could take the place. The Higgs bosons would be the plus ones replaced in the resultant particles such that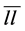 . The neutral Higgs boson could be the one replaced in neutral mediating vector bosons
. The neutral Higgs boson could be the one replaced in neutral mediating vector bosons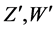 .
.
The scattering amplitude for the diagrams in Figure 1 and Figure 2 can be written down by using the amplitude evaluated for the 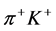 scattering in [5] as
scattering in [5] as
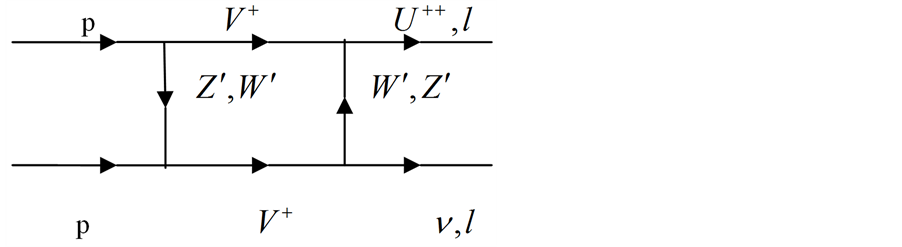
Figure 1. The diagram for the decay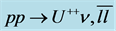 .
.
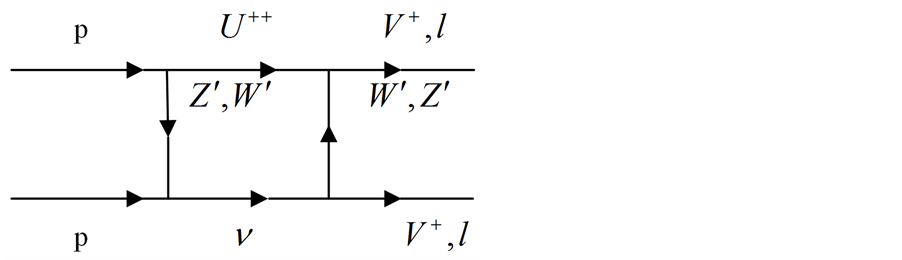
Figure 2. The diagram for the decay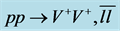 .
.
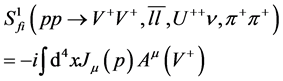 (7)
(7)
where
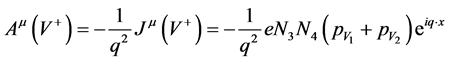 (8)
(8)
with
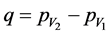 (9)
(9)
and 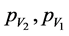 are the four momentum of the resultant particles. The 4-curent for proton is:
are the four momentum of the resultant particles. The 4-curent for proton is:
![]() . (10)
. (10)
Since the protons have the same 4-momentum it is true to write down:
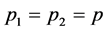 (11)
(11)
Therefore, the exponential term not written in Eqn. (10) is 1. The scattering amplitude can be written as
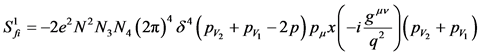 (12)
(12)
Again the waves for both of two protons must be the same, so 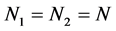 is taken in Equation (12). In Equation (12) the
is taken in Equation (12). In Equation (12) the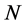 ,
, 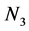 , and
, and 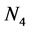 are the normalization factors;
are the normalization factors; 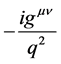 is the propagator for the mediating bosons; q refers to the momentum differences between the final and the initial states, and the four-momenta conservation is given by the term
is the propagator for the mediating bosons; q refers to the momentum differences between the final and the initial states, and the four-momenta conservation is given by the term 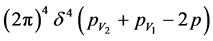 for incoming and outgoing particles.
for incoming and outgoing particles.
3. Conclusion
Although the SM has some difficulties, it is strongly a correct model to extend at the GUT scale. By using the previous works the W' gauge boson mass is estimated to be around 498 GeV. The resultant particles from pp collisions are assumed to be a double positive-electron charged vector boson with a neutrino or anti-neutrino, or, two vector bosons each with one positive-electron charge, instead of the latter one; two anti-leptons are also accepted except the neutrinos. The pp collisions at GUT scale will give the scattering amplitudes as done in this work.
Acknowledgements
I would like to thank to Prof. Dr. Durmuş Ali Demir for his opinions in studying this subject.
References
- Dib, C. and Gilman, J.F. (1987) Physical Review D, 36, 1337-1343. http://dx.doi.org/10.1103/PhysRevD.36.1337
- Arslan, H. (2008) Extra Gauge Bosons in E6 Models, Ph.D. Thesis, Cukurova University, Adana.
- Aydemir, A., Arslan, H. and Topaksu, A.K. (2009) Physics of Particles and Nuclei Letters, 6, 496-503. http://dx.doi.org/10.1134/S1547477109040049
- Aitchison, I.J.R. and Hey, A.J.G. (1982) Gauge Theories in Particle Physics. Adam Hilger, London.
- Greiner, W., Schramm, S. and Stein, E. (2002) Quantum Chromodynamics. Springer-Verlag, Berlin, Heidelberg.

