Journal of Modern Physics
Vol.5 No.4(2014), Article ID:43096,8 pages DOI:10.4236/jmp.2014.54025
Spectral Modifications of Graphene Using Molecular Dynamics Simulations
Department of Applied Science, Bonn-Rhine-Sieg University of Applied Sciences, Rheinbach, Germany
Email: christina.oligschleger@h-brs.de
Copyright © 2014 David Liesegang, Christina Oligschleger. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property David Liesegang, Christina Oligschleger. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received December 16, 2013; revised January 15, 2014; accepted February 14, 2014
Keywords: Molecular Dynamics; Graphene; Nano-Systems
ABSTRACT
We investigated graphene structures grafted with fullerenes. The size of the graphene sheets ranges from 6400 to 640,000 atoms. The fullerenes (C60 and C240) are placed on top of the graphene sheets, using different impact velocities we could distinguish three types of impact. Furthermore, we investigated the changes of the vibrational properties. The modified graphene planes show additional features in the vibronic density of states.
1. Introduction
In nano-technology the influence of the vibrational density of states is of great importance for the dynamic and thermodynamic properties of devices. Since its discovery in 2004 [1] graphene has attracted much attention which is reflected by a large amount of publications in the last years dealing with synthesis, structure and properties [2- 7]. For a comprehensive review and further reading we address reference [8]. Due to the extraordinary properties of graphene in different area, e.g. semi-conductivity (tunable band-gap) [9], its light absorbance [10] or the high values of thermal conductivity [11] its applications range from electric devices to construction chemistry. From experimental results the interaction between C60- fullerene and graphene is known to lead to modifications in the vibrational modes [12,13]. In the field of molecular dynamics simulation a major limitation is mainly caused by the system sizes, the new field of nanotechnology offers a promising area for the modelling community to study systems which are of the same size as the one under experimental considerations, i.e. nanosystem are the interface for both simulations and experiments. Due to parallel computing system, sizes of the order of 107 atoms are available and comparable to experimental structures. One aspect of our simulations is to investigate vibrational properties of graphene, additionally we focus on the modifications of the spectra depending on the structural changes of the graphene flakes induced by buckminsterfullerenes of different sizes. Therefore, we performed molecular dynamic simulations in order to calculate the Fouriertransform of the velocity-autocorrelation function. The fabrication process of the modifactions is performed in two strategies, the first method describes the deposition of fullerenes on top of the graphene sheet. In this case the fullerenes possess different impact velocities before they collide with the graphene. Here it is interesting to see the reactions of the two structures depending on the strength of the impact, i.e. whether the system is intact and the molecules form bonds, are deformed or even destroyed in the respective situation. For our simulation we use a classical molecular-dynamics approach which is a state of the art method for more than three decades [14-17], but which is also recently used for the study of different surface effects [18-21]. Interfaces between crystals and melts are also subject of numerical investigations elucidating both kinetic behaviour and free energies, [22-25]. Nevertheless, one should have in mind that in nano-systems the physics is governed and dominated by quantum effects which are not considered in this type of simulation.
So, electronic contributions are neglected and only atomic/ vibronic behaviour is taken into account. Since the system sizes, which we consider exceed 1000 atoms, our simulations could not easily be transferred to quantummechanical calculations, however these would be helpful. To our knowledge we present here the first systematic study in order to investigate the influence of fullerenes on the frequency spectra of graphene. The article is organized as follows: in the next chapter we give an overview over the models and the potential mimicking atomic interactions used throughout the simulations, and describe computational details. The results of structural and vibrational properties are presented in the third chapter, followed by a discussion. In the final chapter we summarize and give conclusive remarks.
2. Models, Potential and Computational Details
For our investigations we combine graphene planes of different sizes and two types of fullerenes. We built three graphene structures with N = 6400, N = 25,600 and N = 640,000 atoms, the lateral side-lengthes ranging from a = 100.46 Å to 1004.6 Å and b = 174.00 Å to 1740.0 Å. Two types of fullerene structures are used in the simulation, i.e. C60 and C240. The combination of the two basic structures to one ensemble is processed in two ways. In a first type of procedure the fullerenes (both C60 and C240) are placed at a distance of about 2 to 3 Å on top of the graphene and are accelerated to have impact velocities of upto 3300 m/s. In pre-liminary tests we applied very high velocities in order to account for the point of destruction and to identify different impact scenarios. In a second type of alignment a C240-fullerene is directly attached in a distance of 1.0 Å to 1.5 Å to the graphene sheet. The atoms are given randomly distributed initial velocities to establish a well-defined temperature. The influence of the fullerenes on the graphene sectrum is studied using five different setups, in the following denoted as Setup 1 - 5. The first structural combination comprises 6400 atoms in a graphene layer with sides of length a = 100.46 Å, b = 174.00 Å, and on top of the graphene plane a C60-fullerene is placed, which hits the graphene plane with an impact velocity of about 266.5 m/s. The total observation time is 400 ps at 120 K (Setup 1). In order to check the influence of the size of the fullerenes a C240- fullerene is placed in a distance of 2.7 Å on top of the plane and is accelerated towards the graphene layer. Furthermore, different forces are applied on the fullerenes, and henceforth different accelerations are acting on the fullerenes in order to change the final impact velocities onto the graphene sheet. These velocities ranged from 66.7 m/s upto 667 m/s. These structures are aged for 720 ps at 120 K (Setup 2). To reduce the long simulation times we placed a C240-fullerene within a bond-length on top of the graphene plane (6400 atoms) and observed the system for 88 ps (Setup 3). A larger system comprising 25,600 atoms within a graphene plane with a side-length a = 200.9 Å and b = 348.0 Å, and a C240-fullerene attached within one Ångstrom to the layer, is aged for 20 ps at 120 K (Setup 4). The largest systems is constituted by a graphene flake of 640,000 atoms with lateral dimensions of a = 1004.6 Å and b = 1740.0 Å and a C240- fullerene. As for the smallest graphene system, we used different impact velocities to drop the fullerene onto the graphene plane (Setup 5). All the above described structures are based on carbon-configurations. For the simulations of the carbon-structures we used the potential proposed and fitted by D.W. Brenner [26]. This potential is originally designed to describe hydrocarbon molecules, graphite and diamond structures. In Equation (1) we give the functional form of the atomic interactions. The potential consists of two-body (including short-range attractive and repulsive interactions) terms describing the bonding energy Eb
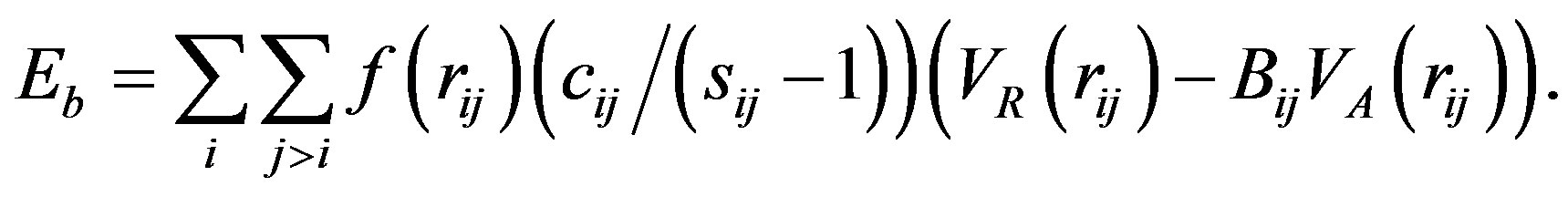 (1)
(1)
Here VR(rij) is the repulsive part of the potential, which is given by  and VA(rij) is attractive and given by
and VA(rij) is attractive and given by
 and the factor Bij describes the averaged bonding situation of atoms i and j at a distance rij. The potential form is analogous to a Morse-type potential. The parameter cij scales the depth of the bonding energy, the other parameters sij, βij reflect type-specific properties and rij,0 corresponds to the equilibrium distance of atoms of type i and j. Equation (2) is the function f(rij), which has a short interaction range and is given by:
and the factor Bij describes the averaged bonding situation of atoms i and j at a distance rij. The potential form is analogous to a Morse-type potential. The parameter cij scales the depth of the bonding energy, the other parameters sij, βij reflect type-specific properties and rij,0 corresponds to the equilibrium distance of atoms of type i and j. Equation (2) is the function f(rij), which has a short interaction range and is given by:
 (2)
(2)
We applied periodic boundary conditions to reduce surface effects caused by the system size. The starting volume is conserved within the simulation and we monitored the virial of the configuration to account for internal pressure. In order to measure structural changes or to show vice versa the stability of the configurations, we introduce the distance between the starting reference phase and the aged ensembles as quantifiable observable. The atomic shifts are measured and are gained from the squared displacements  where
where
 is the position vector of atom n in configuration i of the potential energy surface and Rn is the position of atom n in the reference system. The total displacement ΔR which account for the structural changes is given by ΔR = (ΔR2)1/2 and measured in Ångstrom. The temperatures in the simulations are determined from the velocities of the atoms. In canonical simulations (NVT-ensemble) the velocities of the atoms are rescaled each 100 time-steps in order to keep the temperature constant. To measure the frequencies of the atomic motions we investigate the velocity-autocorrelation function (VACF). The VACF exhibits typical fluctuations of the structures which can be used to determine the underlying vibrations. In our simulation we used Equation (3) to determine the VACF:
is the position vector of atom n in configuration i of the potential energy surface and Rn is the position of atom n in the reference system. The total displacement ΔR which account for the structural changes is given by ΔR = (ΔR2)1/2 and measured in Ångstrom. The temperatures in the simulations are determined from the velocities of the atoms. In canonical simulations (NVT-ensemble) the velocities of the atoms are rescaled each 100 time-steps in order to keep the temperature constant. To measure the frequencies of the atomic motions we investigate the velocity-autocorrelation function (VACF). The VACF exhibits typical fluctuations of the structures which can be used to determine the underlying vibrations. In our simulation we used Equation (3) to determine the VACF:
 (3)
(3)
where vi(0) is the velocity vector of atom i at the reference time and vi(t) is the velocity at time t of atom i. Applying the Cosine-transform of the velocity—autocorrelation function from Equation (4) results in the vibrational density of states (DOS) and is given by Z(ν):
 (4)
(4)
with tobs being the observation time for the velocityautocorrelation function, λ is a damping factor which broadens the peaks in the frequency spectrum [27-29] and Z0 being a normalization constant.
3. Results
In one aspect of our simulations we focus on the stability of graphene flakes which are targeted by smaller objects, e.g. fullerenes. For the investigations of the stability of the graphene we used a layer comprising 6400 atoms loaded by a C240-fullerene with impact velocities of upto 3330 m/s. We can distinguish three different scenarios of collisions depending on the velocities with which the fullerene impacts the graphene. A first type of collision leads to a binding between the two structures, i.e. for impact velocities less than 2000 m/s we observe the graphene layer to be indented by the fullerene. However, both structures the fullerene and the graphene remain stable and bonds are built between the two structures. In a second type of impact we use higher velocities for the buckminsterfullerene. Applying impact velocities ranging from 2000 m/s upto 2700 m/s the fullerene locally destroys the graphene layer. Only few bonds between the strongly deformed fullerene and the atoms at the lacerated rim are established, which weakly bind the fullerene to the graphene. In the third case of impact scenario we applied velocities larger than 2700 m/s. In such a situation the fullerene penetrates the layer. After a few picoseconds the strongly deformed fullerene leaves a hole in the otherwise intact graphene structure. The main focus in our simulations is laid on the modifications in the vibrational spectrum of graphene flakes stressed by fullerenes, i.e. we investigate the changes in the vibrational density of states of graphene structures of different sizes induced by fullerenes.
3.1. Setup 1: C60-Fullerene Impacting a Small Graphene Flake
Firstly let us consider a C60-fullerene with an impact velocity of 266.5 m/s onto a graphene flake of 6400 atoms. After the impact the fullerene causes wavelike displacements in the atomic positions within the graphene similar to those waves caused by a stone thrown into the water. In course of the simulation these waves are damped, however their influence on the vibrational density of states can be clearly seen. After the application of a C60-fullerene on the layer comprising 6400 atoms, we measured the DOS of the structure at two times, the result is shown in Figure 1. The spectra are measured after an observation period of 72 ps, see Figure 1(a), and the DOS after 400 ps is presented in Figure 1(b). For comparison the spectrum of non-decorated graphene is shown (see the green line in Figure 1). In the high-frequent part of the spectra for the

Figure 1. The density of states Z(ν) is plotted vs. the frequency ν in THz. Green line: Vibrational DOS of the graphene sheet. Red line: Vibrational density of states of 6400 atoms grafted with a C60-fullerene. In panel (a) the spectrum after an observation time of 72 ps is presented. Panel (b) shows the frequency spectrum after an observation time of 400 ps.
modified graphene sheets we observe a small additional peak at 54 THz, which is not present in the spectrum of “pure” graphene. However, the main peak in the highfrequency part of the spectrum is shifted towards slightly smaller values, i.e. from 50.4 THz to 49.4 THz, and to slightly reduced intensities compared to the plain graphene structure. Moreover, the part of the spectrum with frequencies larger than 25 THz is reduced in its intensity after the application of the C60-fullerene.
In case of frequencies less then 25 THz we find an increase of intensities in the DOS which exhibit to be time dependent. Another feature of the spectrum which is modified by the application of the fullerene is the broad peak with shoulder ranging from 15 THz to 24 THz. This part of the spectrum is slightly shifted to higher frequencies. After a short time-relaxation of 72 ps, cf. Figure 1(a), two additional low-frequent peaks are measured at 8.6 THz and at approximately 0.6 THz. After a total observation time of 400 ps, see Figure 1(b), the peak at lower frequency vanishes, and the peak at 8.6 THz becomes more pronounced.
3.2. Setup 2: C240-Fullerene Impacting a Small Graphene Flake
To investigate whether there is an influence of the size of buckminsterfullerenes we substitute the C60-fullerene by a C240-fullerene. Here, we followed two routes to combine the C240-fullerene with the graphene flake. Firstly we used the above described impact route to link the C240-fullerene to the grapheme sheet. Again we focus on the changes of the frequency spectrum. As one can see from Figure 2, the impact of the C240-fullerene (with an impact velocity of 66.7 m/s) on the graphene with 6400 atoms reduces the intensity of the high-frequency peaks, however the position of the peaks are not changed compared to the plain graphene spectrum. In the low-frequent region of the DOS an additional peak (not present in the plain graphene spectrum) occurs at 8.6 THz. Due to the fullerene’s impact the graphene structure exhibits wavelike motions which change the density of states. At the beginning of the simulation a high intensity is observed in the limit of long wave-length. The resulting Z(ν) is shown in Figure 2(a) and is obtained after 68 ps A low-frequent feature can be clearly seen for frequencies less than 2 THz. Similar to the simulation with the smaller fullerene this peak is not detected after 720 ps, cf. Figure 2(b). In both sub-figures the green lines show the DOS of the plain graphene structure with 6400 atoms, whereas the red lines display the spectrum of graphene linked with fullerene. The above described systems start from a not equilibrated point in the phase space. At the early stages of the simulation the systems are still in non-equilibrium states and therefore, one can observe
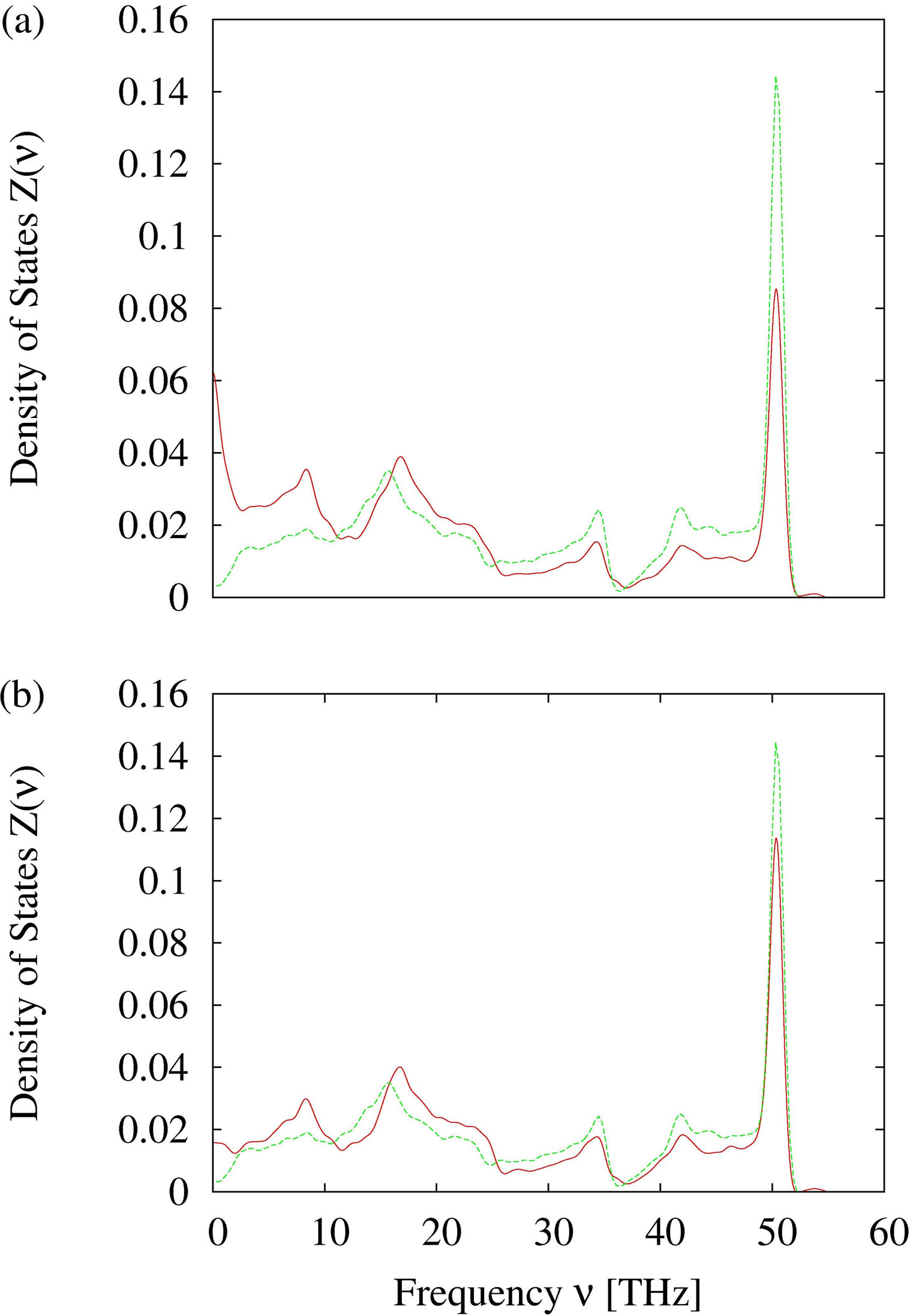
Figure 2. The density of states Z(ν) is plotted vs. the frequency ν in THz. Green line: Vibrational DOS of the graphene sheet. Red line: Vibrational density of states of 6400 atoms grafted with a C240-fullerene. In panel (a) the frequency spectrum after an observation time of 68 ps is presented. Panel (b) shows the frequency spectrum after an observation time of 720 ps.
large fluctuations in all monitored variables during which the systems equilibrate to lower energetic states. This can also be seen in the total displacement, which shows a wave-like behaviour at the beginning of the simulation, followed by the typical small fluctuations. The “first waves”/peaks in ΔR—in connection with the individual trajectories—results from the impact of the fullerene with the graphene plane. The atoms in the vicinity of the impact are elongated in z-direction and this disturbation spreads through the complete system leading to wavelike motions which results in respective fluctuations in the displacement ΔR. After the propagation of these waves, structural relaxations take place and the temporal displacements become randomized. In order to shorten the process of equilibration we apply a different method of implementing the fullerene on the graphene layer.
3.3. Setup 3: C240-Fullerene Placed on Top of a Small Graphene Flake
Not only the influence of different types of fullerenes are investigated, we also want to study the influence of the process to implement a fullerene on a graphene layer with 6400 atoms. The C240-fullerene is directly placed on top of the graphene flake. The distance between the two carbon structures is choosen to be about 1.5 Å, such that atomic bonds are generated at the beginning of the simulation avoiding the impact of the fullerene (which generates wave-like motions in the graphene-flake). After an observation time of 88 ps, we determine the vibrational density of states as shown in Figure 3. As in the previous graphs, the green line depicts the DOS of the graphene flake and the red line shows the spectrum of the graphene with a fullerene attached directly to the plane. In the high-frequent part of the spectrum we find a very small peak at 54 THz. Otherwise the intensities of frequencies larger than 25 THz are reduced compared to the reference spectrum of the graphene sheet. In the low-frequent region we find—as in the other simulations—an additional peak at 8.6 THz. Similar to the results of the simulations including a C60-fullerene the intensities of frequencies less than 25 THz are slightly increased compared to the graphene spectrum, see green line in Figure 3. A slight shift of the broad feature around 15 THz to higher frequencies is also observed in the grafted graphene sheet. The resulting spectrum obtained after an observation period of 88 ps resembles the DOS of the graphene-fullerene ensemble generated by an impact after a relaxation time of 720 ps (see Figure 2(b)). Especially in the low-frequent part of less than 1 THz the intensity is strongly reduced compared to the spectrum obtained after impact at a relaxation period of 68 ps (see Figure 2(a)). This way of combining the two sub-structure reduces the computation time by a factor of eight.
3.4. Setup 4: C240-Fullerene Placed on Top of a Medium-Sized Graphene Flake
To check the influence of the size of the graphene plane we attached a C240-fullerene to a graphene layer with 25,600 atoms. As before, we measure the vibrational spectrum by the Fourier-transformation of the VACF.
The spectra are obtained after different oberservation

Figure 3. The density of states Z(ν) is plotted vs. the frequency ν in THz. Green line: Vibrational DOS of the graphene sheet. Red line: Vibrational density of states of 6400 atoms grafted with a C240-fullerene placed directly on top of the layer. The spectrum after an observation time of 88 ps is presented.
periods and are given in Figure 4. The resulting spectrum (red line shown in Figure 4(a)) is taken after an observation time of 4 ps and compared to the non-modified graphene spectrum, (green line). Despite the fact that the high-frequent peak has the same position in both structures, the intensity of the prominent high-frequent vibration is strongly reduced, if the fullerene is attached to the graphene. In the modified structure an additional peak exhibits at 8.6 THz, i.e. at the low-frequent part of the DOS, and this peak becomes better expressed in course of observation time. The broad feature at intermediate frequencies is shifted about one tera-hertz from 15.8 THz in the plain graphene spectrum to 16.8 THz in the modified density of states, as one can see in Figure 4(b). The peaks of the low-frequent region are clearly developed after an simulation time of only 17 ps. This spectrum of a graphene with a C240-fullerene placed directly on top is similar to the one gained by a (slightly) impact of C240- fullerene. The only difference is in the low-frequency part at which one can observe an increase of the intensity which is due to larger size of the graphene layer. In larger structures acoustic modes of lower frequency are present and an increase of the low-frequent part of the DOS can be explained.

Figure 4. The density of states Z(ν) is plotted vs. the frequency ν in THz. Green line: Vibrational DOS of the graphene sheet. Red line: Vibrational density of states of 25600 atoms grafted with a C240-fullerene. In panel (a) the spectrum after an observation time of 4 ps is presented. Panel (b) shows the frequency spectrum after an observation time of 17 ps.
3.5. Setup 5: C240-Fullerene Impacting a Large Graphene Flake
In the largest system, which is studied, we connect a graphene layer comprising 640,000 atoms and a C240- fullerene. The fullerene hits the graphene with an impact velocity of 66.7 m/s followed by structural relaxations, the temperature of the system is held constant at 120 K. After the impact of the fullerene onto the graphene plane wave-like motions are evolving and spreading through the graphene. The total observation time of this system is 43 ps. As in the previous simulations we measured the velocity-autocorrelation function (see Equation (3)) and gained the frequency spectrum via Fourier-transformation (cf. Equation (4)). To check whether there exist time dependent effects, we calculated the density of states at an early stage of the simulation, i.e. after 5 ps, and at the end of the total observation period. The resulting spectra are shown in Figure 5. The green line shows the vibrational density of states of the graphene sheet with 640,000 atoms. The red line in Figure 5(a) shows the frequency spectrum which we obtained at 5 ps the after impact of the fullerene on the graphene. In Figure 5(b) the red line gives the DOS of the grafted graphene after an observation time of 43 ps. In contrast to the previous observations there is no additional peak at 54 THz in the spectrum of the largest modified graphene. However, the intensities of higher-frequent vibrations are reduced in the modified graphene structure whereas the lower-frequent part has higher intensities. Compared to the plain graphene sheet an additional peak at 8.6 THz is clearly seen in the grafted graphene. Also a small shift of the peak at 15.8 THz in the plain structure to 16.8 THz in the modified graphene is observed.
4. Discussion
The focus of our simulation is mainly laid on vibrational properties of carbon systems comprising graphene layers and fullerenes molecules. The interpretation of our results is purely qualitative. For the simulation of an impact of a C240-fullerene onto the plane of a graphene flake, we distinguish three qualitatively different types of impacts. The first type leads to a weak bonding situation between the fullerene and the graphene layer, i.e. few carbon atoms change the initial coordination number from 3 (planar bonding) to 4 (tetrahedral bonding), which is possible since the hybridization of these atoms is changed from sp2 to sp3. Such an alignment may be considered in analogy to the reaction of two molecules. The impact and the subsiding interaction is connected with a relatively small impact velocity or better small impetus of the fullerene molecule. This type of impact leaves the individual structures almost undeformed. On the graphene layer smooth wiggles are induced and the buckminster

Figure 5. The density of states Z(ν) is plotted vs. the frequency ν in THz. Green line: Vibrational DOS of the graphene sheet. Red line: Vibrational density of states of 640000 atoms grafted with a C240-fullerene. In panel (a) the spectrum after an observation time of 5 ps is presented. Panel (b) shows the frequency spectrum after an observation time of 43 ps.
fullerene flattens. The second type of impact with an intermediate impact velocity results in a trough impressed in the graphene. The stronger the impetus is the deeper the trough is which is “filled” by the fullerene. In all these cases, the number of sp3-hydridised carbons is strongly increased compared to the first type of impact. If the impact velocity is larger than 2700 m/s, i.e. the impetus of the fullerene is about 1.31 × 10−20 kg m/s and its kinetic energy is 1.77 × 10−17 kg m2/s2, resp., the graphene is locally crashed by the fullerene. If we use the volume of destroyed part of the graphene layer we can estimate the pressure induced in the graphene to be about 30 GPa. Using two methods of applications, the fullerenes, i.e. C60- and C240-fullerene, are attached to graphene layers. After a relaxation period the vibrational density of states are measured by Fourier-transformation of the velocity-autocorrelation function. The firstly applied method in which the fullerenes collide with the graphene flake seems to be a rather natural way of simulation setup, however it is rather time consumive since the induced wavelike motions will be spread through the graphene layer and be damped in course of observation time via relaxation processes These wavelike motions will influence the spectra measured shortly after impact. To determine the spectra of the equilibrated structures one has to perform rather long simulations. To shorten the long relaxation period we introduced a second type of experiment in which the structures are attached without using an impact energy. Therefore, the relaxation period is drastically reduced, since the via impact locally introduced heat must not be transported or distributed throughout the whole ensemble. However, the resulting spectra are similar and show comparable/identical features. If we look for prominent modifications which occur in our simulations we observe a small additional peak at 54 THz, which neither is seen in the original spectrum of graphene nor is present in the largest modified graphene structure. A reduction of the peak intensity for frequencies larger than 25 THz is observed in all the cases studied in our simulations. Connected to this intensity reduction is an increase of the peak intensities of vibrations less than 25 THz. Also a small shift of the frequency region located at 15 THz in the graphene spectrum to higher values in the modified spectra is observed in our simulations. The strongest change in the modified spectra turned out to be an additional peak which cannot be seen in the spectrum of a “pure” graphene layer. In the lowfrequent part of the DOS a peak around 8.6 THz becomes a prominent feature of the modified spectra whereas in the non-modified vibrational states there is no peak at this position. Comparison of the two types of fullerenes shows that the application of the smaller one, i.e. the C60- fullerene, causes not only a reduction of the high-frequent intensity but also leads to a shift in the peak position from 50.4 THz down to 49.4 THz. In contrast to that observation the application of a C240-fullerene only reduces the intensity of the still prominent high-frequent peak and leaves its position unchanged.
5. Summary
We have shown that systematic application of fullerenes has influence on the density of states of graphene flakes. Especially in the low-frequent region the intensities are increased and an additional peak at 8.6 THz is generated. The early stages of the simulation (due to equilibration process) lead to a (very) low-frequent peak. We could demonstrate that this peak at very low frequencies vanishes in course of time due to equilibration. In order to shorten the simulation period and to avoid the initial states of non-equilibrium we introduce a second method of application. Using this type of application we find in a much shorter simulation period the same remarkable shifts of peaks or additional low-frequent peaks in the graphene flakes. Changes in the vibrational density of states are typically connected with changes of thermodynamic properties, e.g. thermal conductivity or specific heat. Therefore, possible tailored design of frequency spectra and the subsequent dynamic or thermodynamic properties of graphene flakes could broaden the usage of this interesting material.
REFERENCES
- K. S. Novoselov, et al., Science, Vol. 306, 2004, pp. 666- 669. http://dx.doi.org/10.1126/science.1102896
- D. C. Elias, et al., Science, Vol. 323, 2009, pp. 610-613. http://dx.doi.org/10.1126/science.1167130
- J.-C. Charlier, P. C. Eklund, J. Zhu and A. C. Ferrari, “Electron an Phonon Properties of Graphene: Their Relationshop with Carbon Nanotubes,” In: A. Jorio, G. Dresselhaus and M. S. Dresselhaus, Eds., Carbon Nanotubes: Advanced Topics in the Synthesis, Structure, Properties and Applications, Springer-Verlag, Berlin, 2008. http://dx.doi.org/10.1007/978-3-540-72865-8_21
- K. S. Novoselov, et al., Nature, Vol. 438, 2005, pp. 197- 200. http://dx.doi.org/10.1038/nature04233
- S. V. Mozorov, et al., Physical Review Letters, Vol. 100, 2008, Article ID: 016602. http://dx.doi.org/10.1103/PhysRevLett.100.016602
- J. H. Chen, C. Jang, S. Xiao, M. Ishigami and M. S. Fuhrer, Nature Nanotechnology, Vol. 3, 2008, pp. 206- 209. http://dx.doi.org/10.1038/nnano.2008.58
- A. Akturk and N. Goldsman, Journal of Applied Physics, Vol. 103, 2008, Article ID: 053702. http://dx.doi.org/10.1063/1.2890147
- S. M. Lindsay, “Introduction to Nanoscience,” Oxford University Press, New York, 2010.
- Y. Zhang, et al., Nature, Vol. 459, 2009, pp. 820-823. http://dx.doi.org/10.1038/nature08105
- R. R. Nair, et al., Science, Vol. 320, 2008, p. 1308. http://dx.doi.org/10.1126/science.1156965
- A. A. Balandin, et al., Nano Letters, Vol. 8, 2008, pp. 902-907. http://dx.doi.org/10.1021/nl0731872
- D. Yu, K. Park, M. Durstock and L. Dai, Journal of Physical Chemistry Letters, Vol. 2, 2011, pp. 1113-1118. http://dx.doi.org/10.1021/jz200428y
- Y. Zhang, L. Ren, S. Wang, A. Marathe, J. Chaudhuri and G. Li, Journal of Material Chemistry, Vol. 21, 2011, pp. 5386-5391. http://dx.doi.org/10.1039/c1jm10257e
- P. Hansen and I. R. McDonald, “Theory of Simple Liquids,” Academic, New York, 1976.
- G. Cicotti, D. Frenkel and I. R. McDonald, “Simulations of Liquids and Solids,” North Holland, Amsterdam, 1987.
- M. P. Allen and D. J. Tildesley, “Computer Simulation of Liquids,” Clarendon, Oxford, 1987.
- B. J. Garrison, Chemical Society Reviews, Vol. 21, 1992, pp. 155-162. http://dx.doi.org/10.1039/cs9922100155
- L. Ding, C. Gung, Y. Zhao, X. He and H. Wen, Science in China Series B: Chemistry, Vol. 51, 2008, pp. 651-660.
- A. Schüring, J. Gulín-González, S. Fritzsche, J. Kärger and S. Vasenkov, Diffusion Fundamentals, Vol. 6, 2007, pp. 33.1-33.2. http://www.uni-leipzig.de/~diff/pdf/volume6/diff_fund_6(2007)33.pdf
- A. Ito and H. Nakamura, Communication in Computational Physics, Vol. 4, 2008, pp. 592-610. http://www.global-sci.com/
- P. Valentini and T. Dumitrica, Journal of Nano Research, Vol. 1, 2008, pp. 31-39. http://www.scientific.net/jnanor http://dx.doi.org/10.4028/www.scientific.net/JNanoR.1.31
- A. Brinkmann, et al., Physica B, Vol. 406, 2011, pp. 2931-2947. http://dx.doi.org/10.1016/j.physb.2011.02.074
- R. L. Davidchack and B. B. Laird, Molecular Physics, Vol. 97, 1999, pp. 833-839. http://dx.doi.org/10.1080/00268979909482884
- R. L. Davidchack and B. B. Laird, Physical Review Letters, Vol. 85, 2000, pp. 4751-4754. http://dx.doi.org/10.1103/PhysRevLett.85.4751
- M. Amini and B. B. Laird, Physical Review Letters, Vol. 97, 21, 2006, Article ID: 216102. http://dx.doi.org/10.1103/PhysRevLett.97.216102
- D. W. Brenner, Physical Review B, Vol. 42, 1990, pp. 9458-9471. http://dx.doi.org/10.1103/PhysRevB.42.9458
- D. Beeman and R. Alben, Advances in Physics, Vol. 26, 1977, pp. 339-361. http://dx.doi.org/10.1080/00018737700101403
- C. Oligschleger and J. C. Schön, Journal of Physics: Condensed Matter, Vol. 9, 1997, pp. 1049-1066. http://dx.doi.org/10.1088/0953-8984/9/5/011
- C. Oligschleger, et al., Journal of Physics: Condensed Matter, Vol. 21, 2009, Article ID: 405402. http://dx.doi.org/10.1088/0953-8984/21/40/405402

