Journal of Modern Physics
Vol.5 No.1(2014), Article ID:42058,6 pages DOI:10.4236/jmp.2014.51003
Non-Linear Forces and Irreversibility Problem in Classical Mechanics
Institute of Ionosphere, Kamenskoe Plato, Almaty, Kazakhstan
Email: vmsoms@rambler.ru, mokhnatkin@gmail.com
Received November 17, 2013; revised December 15, 2013; accepted January 4, 2014
ABSTRACT
Restrictions of classical mechanics which take place because of holonomic constraints hypothesis used for obtaining canonical Lagrange equation are analyzed. As it was shown that this hypothesis excludes non-linear terms in the expression for forces which are responsible for energy exchange between different degrees of freedom of a many-body system. An oscillator passing a potential barrier is considered as an example which demonstrated this fact. It was found that the oscillator can pass the barrier even if kinetic energy of its mass center is below the potential barrier’s height due to non-linear terms. This effect is lost because of holonomic constraints hypothesis. We also explained how one can derive a system’s motion equation without the use of holonomic constraints hypothesis. This equation can be used to describe non-linear irreversible processes within the frames of Newton’s laws.
Keywords:Holonomic Constraints; Non-Linear Energy Transformation; Irreversible Processes; Oscillator
1. Introduction
Mechanics study how real bodies change their position by time. The world and evolution are described by space and time. Classical mechanics cannot describe evolution in nature. All processes in nature are irreversible—systems born, developed and died. Classical mechanics describe reversible processes only.
Boltzmann was the first to study this contradiction [1]. He proves that processes in non-equilibrium gas are irreversible, but the proof was denied by Poincare theorem of Hamilton systems comeback [1,2]. The theorem follows from the law of conservation of phase volume which in turn follows from Lagrange and Hamilton equations. Today’s explanation of irreversible dynamics is an eclectic one. It is based on laws of classical mechanics and a suggestion of very small fluctuations. This suggestion cannot be relevant to determinism of classical mechanics.
Recently we offered a mechanism of irreversibility which follows from the laws of classical mechanics only [3-6]. We call this mechanism a determined one. It is based on non-linear transformation of kinetic energy of a system into its internal energy.
What we see is a contradiction. The system’s motion is reversible due to formal descriptions of classical mechanics and at the same time it is irreversible due to the determined mechanism described above. It is obvious that we cannot consider the explanation of irreversibility as a complete one until we resolve this contradiction. We can resolve the contradiction only if irreversibility had been excluded by the simplifications used when obtaining Lagrange equation for systems.
At least two main simplifications are used when obtaining the equation of a system’s motion on the basis of Newton equation for motion of a material point. The first simplification is due to the fact that we use simple models where a real body consists of several material points which have no internal structure. The second simplification follows from the fact that we use hypothesis of holonomic constraints when we obtain Lagrange equation for a system from Newton equation for a material point. Let’s consider these two simplifications.
Classical mechanics is based on Newton’s laws. The Newton’s laws are derived by using structureless material point as a model. But what we see in real life are systems, not the material points. The world has hierarchic nature. Top step is the Universe. It consists of galaxies which in turn consist of other elements. Molecules and atoms are somewhere downstairs. They are systems as well and consist of smaller elements. We don’t know how long this hierarchy is.
We can represent any real body by a system of potentially interacting material points. So the laws of motion of any system should follow from the laws of motion of material points. It is true for both reversible formal descriptions of classical mechanics and irreversible equation of an equilibrium system moving in a nonhomogeneous external field [4]. So we do not exclude irreversibility only because we represent a real body by a set of material points. The only conclusion we can make is that the contradictions are due to some hypotheses which were used while creating formal descriptions of mechanics. We can eliminate the contradictions if we are able to show that these hypotheses resulted in the fact that classical mechanics cannot explain irreversible processes. Holonomic constraints and potential-field forces are used when obtaining the Lagrange and Hamilton equations from d’Alembert equation for a system of the material points [7,8].
Below we explain why irreversible dynamics cannot be described because of holonomic constrains hypothesis. We also consider the difference between mechanics of structured particles and classical mechanics based on the formalisms of Lagrange and Hamilton. After that we consider an example of an oscillator passing a potential barrier. We also show that holonomic constrains hypothesis excludes mutual transformation between the energy of motion of the system and its internal energy. We explain how one can obtain the equation of motion of a system without use of the hypothesis of holonomic constraints. We also explain why the motion equation for real bodies is irreversible in general.
The Classical Way of Deriving a System’s Motion Equation from the Motion Equations of Material Points.
We can derive a system’s motion equation using Lagrange equation and knowledge of dynamics of each material point. Lagrange equation is derived using d’Alembert principle. The d’Alembert principle is given by [8]:
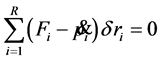 (1)
(1)
Here  is an active force affecting i—material point;
is an active force affecting i—material point;  is i-th material point’s inertial force;
is i-th material point’s inertial force;  is virtual shift.
is virtual shift.
We should use independent generalized variables in order to integrate (1). After we do the transformation needed we obtain the following [8]:
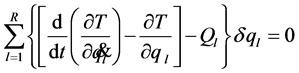 (2)
(2)
Here 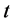 is time;
is time; 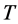 is a kinetic energy for all MP;
is a kinetic energy for all MP; 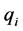 are the general independents variables;
are the general independents variables; 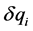 are the virtual transitions;
are the virtual transitions; 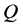 are the external forces.
are the external forces.
Holonomic constraints hypothesis is used in order to derive canonical Lagrange equation from (2). This hypothesis implies that each term in (2) is independent. This fact in turn implies that  coordinates are independent, i.e. a variation of
coordinates are independent, i.e. a variation of  doesn’t depend on variation of
doesn’t depend on variation of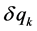 . Therefore, the sum (2) of equals zero when each term of the sum equals zero. If there are external forces, then the abovementioned condition is valid only if external forces do not have non-linear terms depending on several variables. That is, external forces should comply with the following conditions [8]:
. Therefore, the sum (2) of equals zero when each term of the sum equals zero. If there are external forces, then the abovementioned condition is valid only if external forces do not have non-linear terms depending on several variables. That is, external forces should comply with the following conditions [8]:
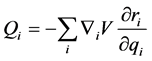 (3)
(3)
Thereby if we use holonomic constraints, then we obtain Lagrange equation where 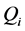 depends on i-coordinates only:
depends on i-coordinates only:
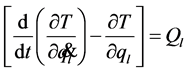 (4)
(4)
That is, holonomic constraints hypothesis excludes interrelations between terms in equation (2), i.e. each term in (2) is independent. The terms in (2) can be dependent only if there is some non-linearity of the external forces. In such case at least two terms in (2) are not equal to zero while the whole sum equals zero. That means the constraints are not holonomic and condition (3) is not relevant.
If condition (3) takes place, then equation (4) could be written as follows [8]:
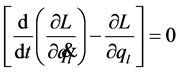 (5)
(5)
where 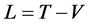 is so-called Lagrange function.
is so-called Lagrange function.
Formula (5) is Lagrange equation. It allows describing a system’s dynamics by studying dynamics of each material point.
From (2) follows that holonomic constraints condition is equivalent to condition of potential external forces. This equivalence also follows from the fact that one and the same Lagrange equation (11) can be obtained also by integrating the d’Alembert equation on time provided the potentiality of external forces. Indeed by integrating d’Alembert equation with respect to time given external forces is potential. If we fix initial and final positions of a system, we obtain [7]:
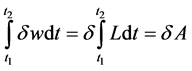 (6).
(6).
If 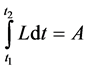 then we have:
then we have:
 (7)
(7)
Formula (7) is Hamilton principle. The principle says that the system’s path is such that value of definite integral A is stationary whenever the fluctuation of the system’s position is, provided the initial and end positions are fixed [7].
According to expression (3), if we apply holonomic constraints condition, then integration of equations of the motion of the whole system of material points is reduced to integration of independent equations of motion of each material point. That is, reversibility follows from holonomic constraints. Therefore, Lagrange and Hamilton equations are reversible as well as Newton’s motion equation.
Thus, Lagrange equation follows from the principle of d’Alembert as a result of the transition to the generalized independent variables. The corresponding equations for the material points are independent due to hypothesis of holonomic constraints [7,8]. Hence we arrive to the canonical Lagrange equations and to the principle of least action. Consequently, the scope of the canonical Lagrange equations and the principle of least action are determined by the generality of hypothesis of holonomic constraints.
Below we consider an oscillator passing a potential barrier as an example. We show that if a system passes through a non-homogeneous filed then we observe completely new effects due to mutual transformation of the energy of motion of a system into its internal energy. We lose these effects if we use holonomic constraints hypothesis. That is why we used energy expressions in order to derive the system’s motion equation. By doing so, we do not have to use holonomic constraints hypothesis. We also do not lose non-linear terms which are responsible for mutual energy transformation between degrees of freedom of the system.
2. Non-Holonomic Constraints for an Oscillator
Consider an oscillator consisting of two material points. Let the first point’s mass be equal to mass of the second one. We can write the oscillator’s total energy as follows:
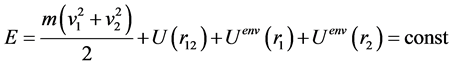 (8)
(8)
where 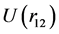 is potential energy of interaction between the material points;
is potential energy of interaction between the material points;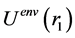 ,
,  are potential energies of the 1st and 2nd material points in the field of external forces;
are potential energies of the 1st and 2nd material points in the field of external forces;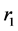 ,
, 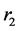 are coordinates of the material points;
are coordinates of the material points;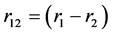 ;
;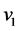 ,
,  are velocities of the material points.
are velocities of the material points.
Now let’s use coordinates of the system’s mass center. Therefore we substitute the variables as follows:
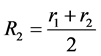 ,
,  (coordinate and velocity of the mass center). Let’s name these variables as macrovariables. At the same time let’s name by microvariables relative coordinate and velocity of the material points:
(coordinate and velocity of the mass center). Let’s name these variables as macrovariables. At the same time let’s name by microvariables relative coordinate and velocity of the material points:
 ,
, 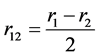 , where
, where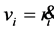 . These new sets of variables are independent. The system’s total energy now can be written as:
. These new sets of variables are independent. The system’s total energy now can be written as:
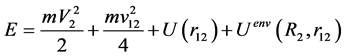 (9)
(9)
Here ;
; 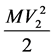 is the system’s mass center kinetic energy,
is the system’s mass center kinetic energy, 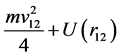 is the oscillator’s internal energy. In turn,
is the oscillator’s internal energy. In turn, 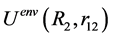 is the system’s potential energy.
is the system’s potential energy.
Now we see that total energy is the sum of the system’s kinetic and internal energies. By differentiating (9) with respect to time, we obtain:
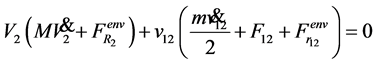 (10)
(10)
where ,
, 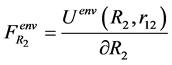 ,
,
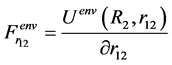 ,
, 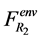 and
and  depends on
depends on 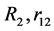
in general.
If there is no external field, then the variables in equation (10) are separated and we can integrate (10).
Let the external field be homogeneous on the system’s typical scale. In that case we obtain two equations from (10):
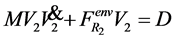 (11)
(11)
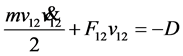 (12)
(12)
Here  is a separation constant. It is obvious that it should be equal to zero.
is a separation constant. It is obvious that it should be equal to zero.
Equation (11) describes the motion of the system’s mass center. Equation (12) describes the relative motion of the material points, which is not affected by external forces. This means that internal energy is constant in case of homogeneous external field.
Thus, we can separate the variables and integrate the system if we can represent the external field by sum of two terms, one depending on macrovariables, and another—on microvariables only. The abovementioned is essentially the same as holonomic constraint and obtaining equation (4) for an oscillator.
The external field’s energy will in general change both the systems kinetic and internal energies [9]. This is the case when the external field has non-linear terms depending on both microand macrovariables. Mutual non-linear transformation between the system’s kinetic and internal energies occurs. That means one cannot separate the variables and integrate the system. Virtually, this is a violation of holonomic constraints.
Numerical calculations were done in order to study non-linear transformation of an oscillator’s kinetic energy into its internal energy. The potential barrier was given by 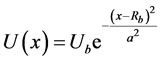 [9]. Here
[9]. Here 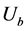 is the barrier’s height;
is the barrier’s height; 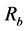 is the coordinate of the barrier’s extreme point; is a barrier’s half-width, x is the axis along which the oscillator is moving.
is the coordinate of the barrier’s extreme point; is a barrier’s half-width, x is the axis along which the oscillator is moving.
The numerical calculations showed that given the barrier’s half-width is comparable to the oscillator’s length, the oscillator can pass the barrier even when its kinetic energy is below the barrier’s height (see figure 1). This resulted from transformation of the oscillator’s internal energy into its kinetic energy due to a gradient of external force (see figure 2). Opposite cases were registered as well (see figure 3). The oscillator didn’t pass the barrier although its kinetic energy was above the barrier’s height. The reason for this was the transformation of the oscillator’s kinetic energy into its internal energy such that the kinetic energy after transformation was not enough to pass the barrier. That is, whether the oscillator passes the barrier or not, depends on the ratio between initial distance to the barrier and the barrier’s half-width. Let us lay emphasis on the fact that these cases cannot be described by canonical Lagrange and Hamilton equations because of non-holonomic constraints.
It was shown [4,5] that in general we can split phase space into two orthogonal subspaces of independent variables for a system of N material points (N ? 1) provided that we use microand macrovariables. Microvariables describe motion of the material points, while macrovariables describe motion of the system’s mass center in the external field. This orthogonality resulted from quadric form of energy. In terms of physics, the orthogonality results from the fact that the material points interaction forces do not dependent on external forces. So the system’s energy is split into two independent types, kinetic energy of material points moving relative the mass center, and the mass center’s kinetic energy depending
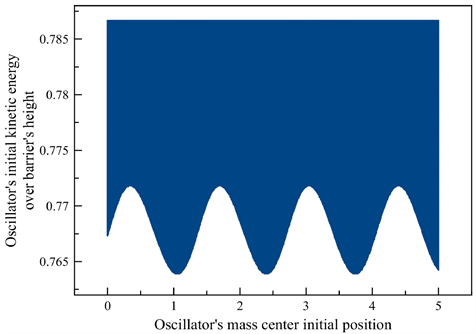
Figure 1. Oscillator passes the potential barrier even if its initial kinetic energy is below the barrier’s height given the oscillator’s length is comparable to the barrier’s half-width (blue points show the cases when the oscillator passed the barrier, while white points show the cases of reflection).
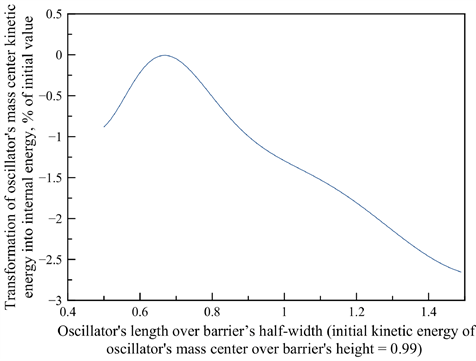
Figure 2. Transformation of oscillator’s kinetic energy as a function of oscillator’s length.

Figure 3. Change of oscillator’s kinetic energy as a result of transformation into internal energy as a function of initial position of the mass center.
on the mass center coordinate and velocity. This is correct for all bodies which can be represented by a number of material points. If external field is not homogeneous on the system’s typical scale, then non-linear terms appear in the system’s motion equation [4]. These nonlinear terms depend on microand macrovariables. In this situation energy of the external field changes both kinetic and internal energies of the system.
There is another way to explain the necessity of splitting variables into microand macrovariables. If we use lab system of coordinates and sum dynamic variables for material points, then we exclude internal forces. The only force left is external force which determines the motion of the system’s mass center. As a result we derive the equation of motion of the system’s mass center. The equation corresponds to macrodescription of the system.
Just the other way around, if we deduct the abovementioned variables, then we exclude external forces and derive the equations which describe relative motion of material points. The equations correspond to microdescription of the system.
Let us explain how an oscillator can pass through potential barrier. Consider the oscillator’s motion equation (10). It is obvious that 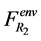 and
and 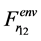 are not equal to zero in case of non-homogeneous external field. These terms depend on both microand macroparameters, i.e. micro and macroparameters are inter-dependant. That is why mutual transformation between the oscillator’s kinetic and internal energy is possible. These terms either increase or decrease the oscillator’s kinetic energy subject to the oscillator’s current position. If the contribution of these non-linear terms is high enough, then the oscillator can pass the barrier even when its kinetic energy is below the barrier’s height. It was already shown that these non-linear terms are inversely related to typical scale of a nonhomogeneous external field [10].
are not equal to zero in case of non-homogeneous external field. These terms depend on both microand macroparameters, i.e. micro and macroparameters are inter-dependant. That is why mutual transformation between the oscillator’s kinetic and internal energy is possible. These terms either increase or decrease the oscillator’s kinetic energy subject to the oscillator’s current position. If the contribution of these non-linear terms is high enough, then the oscillator can pass the barrier even when its kinetic energy is below the barrier’s height. It was already shown that these non-linear terms are inversely related to typical scale of a nonhomogeneous external field [10].
Thus, we should use independent microand macrovariables in order to describe the motion of a real body. These variables correspond to two independent subspaces. So, microand macrovariables split generalized coordinates and velocities space into two independent subspaces. Thus, symmetries of two types determine a system’s motion: material point space distribution symmetry (and material point interaction) and space symmetry itself. Noether theorem says that the system’s motion is determined by the mass center energy and energy of relative motion of material points.
Article [11] considers a system of many material points, such that the system is equilibrium from the point of view of thermodynamics. The motion equation of the system is obtained directly from the energy equation. Total energy is given by the sum of kinetic energy of the system’s mass center and its internal energy. This approach avoids usage of both holonomic constraints hypothesis and hypothesis of potential forces unlike the ways Lagrange equation was obtained [7,8]. It was shown that if the rate of change of external forces is not too high (if it is too high, then the system is not in equilibrium any more), then the internal energy of the system can go up only. The reason is that internal forces cannot change the system’s kinetic moment and thus the system’s internal energy cannot be transformed into kinetic one. That is why the system’s motion is irreversible, i.e. dissipative.
If a system consisting of N ? 1 material points is in equilibrium, then its state is determined by internal energy [4,6]. So we can describe motion of equilibrium systems using macrovariables and internal energy. In general, if an equilibrium system is moving in a field of external forces, then there is a non-linear transformation of its kinetic energy into internal one. This transformation takes place according to non-holonomic constraints.
We can derive generalized Lagrange and Hamilton equations in the same way as we did for canonical equations, but using equations of systems motion and without use of holonomic constraints [4,5].
3. Conclusions
The Lagrange equation is used in order to describe motion of a system of material points. This equation follows from a single material point motion equation by using the hypothesis of holonomic constraints. But because of this hypothesis, the non-linear terms which are responsible for mutual energy transformation between degrees of freedom of the system (between internal energy and motion energy of the system) have been lost. These non-linear terms appear due to gradients of external forces. Numerical calculations showed that due to these non-linear terms, an oscillator can pass the potential barrier even when its kinetic energy is below the barrier’s height, and vice versa, the oscillator can be reflected even if its kinetic energy is above the barrier’s height. Thus, if we use holonomic constraints hypothesis, then we lose these non-linear terms. That is why we cannot use canonical Lagrange and Hamilton equations in order to describe a system in a nonhomogeneous external field. We also cannot use these equations in order to describe the evolution of the non-equilibrium systems to the equilibrium state.
In order to build a formal description that is applicable for describing evolution of the non-equilibrium systems, we should not use holonomic constraints hypothesis when deriving motion equations for a system of material points. Papers [3-6] offer the way to build such formal description. The main idea is to derive a system’s motion equation based on the Newton’s laws and energy formula in which the system’s total energy equals its kinetic energy plus internal energy. The independent macroand micro-variables, which describe a system’s mass center motion and the motion of each material point correspondingly, have been used. Due to such energy split, we are able to take into account non-linear terms which are responsible for mutual energy transformation between system’s motion energy and its internal energy.
The external field should be nonhomogeneous on the system’s typical scale in order for non-linear terms to be essential. For nonequilibrium system, consisting from many equilibrium subsystems, the non-linear transformation of kinetic energy into internal one is equivalent to dissipation, and the forces causing the transformation are actually friction forces. Unlike canonical Lagrange, Hamilton and Liouville equations, their generalized prototypes are able to describe dissipative processes. The generalized Lagrange, Hamilton and Liouville equations are derived from d’Alembert principle by usage of a system’s motion equation rather than motion equations of material points and without use of holonomic constraint hypothesis [5]. As a result these equations contain the terms which are responsible for dissipative processes.
Thus, classical mechanics neglects dissipative processes because of holonomic constraint hypothesis which is used while obtaining the canonical Lagrange equation. This is crucial since almost all fields of physics are based on Lagrange and Hamilton formal descriptions. This is also important in terms of understanding spontaneous symmetry breaking and developing mechanics of dissipative (i.e. evolving) systems.
REFERENCES
- I. Prigogine, “From Being to Becoming,” Nauka, Moscow, 1980
- A. Poincare, “On Science,” Nauka, Moscow, 1983.
- V. M. Somsikov, New Advances in Physics, Vol. 2, 2008, pp. 125-140.
- V. M. Somsikov, Journal of material Sciences and Engineering A, Vol. 1, 2011, pp. 731-740.
- V. M. Somsikov, IJBC, 14, 2004, pp. 4027-4033.
- V. M. Somsikov, Journal of Physics: Conference Series, Vol. 23, 2005, pp. 7-16.
- C. Lanczos, “The Variational Principles of Mechanics,” Academic Press, Waltham, 1962.
- G. Goldstein, “Classical Mechanics,” Nauka, Moscow, 1975.
- V. M. Somsikov and M. I. Denisenya, Izvestiya VUZ, Fizika, Vol. 3, 2013, pp. 95-103.
- V. M. Somsikov, “Nonequilibrium Systems and Mechanics of the Structured Particles,” In: Chaos and Complex System, Elsever, Amsterdam, 2013, pp. 31-39.
- G. M. Zaslavsky, “Stochasticity of Dynamical Systems,” Nauka, Moscow, 1984.

