Journal of Modern Physics
Vol.4 No.12(2013), Article ID:40506,5 pages DOI:10.4236/jmp.2013.412193
A Mechanism for Hadron Molecule Production in 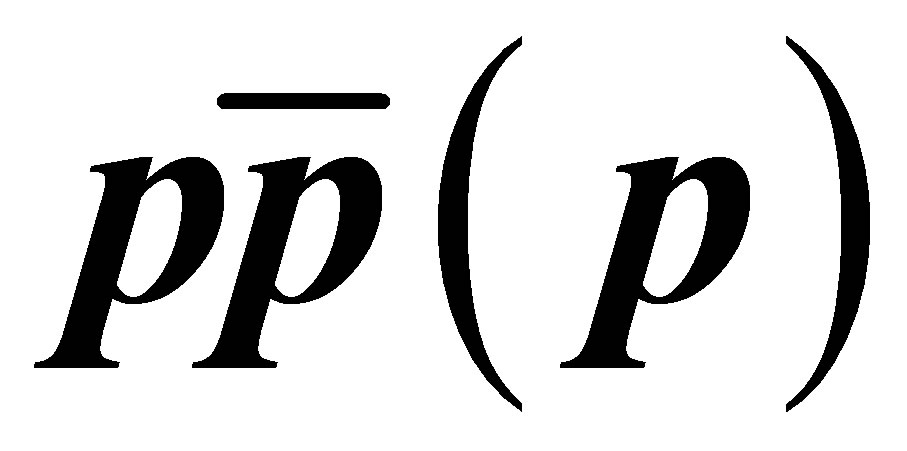 Collisions
Collisions
1Dipartimento di Fisica, Sapienza Università di Roma, Roma, Italy
2Department of Physics, Columbia University, New York, USA
3INFN, Sezione di Pavia, Pavia, Italy
4INFN, Sezione di Roma 1, Roma, Italy
Email: *antonio.polosa@roma1.infn.it
Copyright © 2013 Angelo Esposito et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 17, 2013; revised October 19, 2013; accepted November 16, 2013
Keywords: Exotic Spectroscopy; Heavy Quark Phenomenology; Hadron Scattering; Monte Carlo Simulations
ABSTRACT
The problem of understanding loosely bound hadron molecules prompt production at hadron colliders is still open: how is it possible that meson molecules with binding energy compatible with zero could be formed within the bulk of the hadrons ejected in very high energy collisions? Monte Carlo simulations have been performed in the literature, leading to production cross sections, two orders of magnitude which were smaller than the experimental value. One possible mechanism to reduce this gap could be final state interactions of heavy mesons, but a precise evaluation of such effect is challenged by the presence of pions between the molecular constituents. In this paper, we present a new mechanism by using precisely such comoving pions. Heavy meson pairs can indeed slow down because of elastic scattering with surrounding pions. The number of low-relative-momentum meson pairs increases, thereby enhancing prompt production cross section. In this preliminar simulation, we show that an enhancement of 100 is indeed possible.
1. Introduction
The problem of understanding the loosely bound hadron molecule formation in  collisions at Tevatron and LHC energies is still open. A recent measurement by the CMS Collaboration [1] basically confirms, at higher energies, older Tevatron results on the prompt production of
collisions at Tevatron and LHC energies is still open. A recent measurement by the CMS Collaboration [1] basically confirms, at higher energies, older Tevatron results on the prompt production of 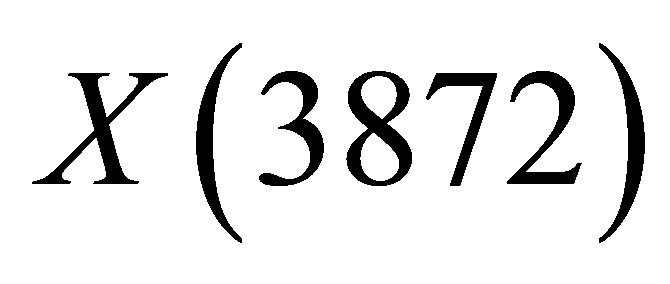 which were first addressed in [2]. Looking at these new results [1], the questions remain the same as those raised in [2]: how is it possible that a very long lived molecule of a
which were first addressed in [2]. Looking at these new results [1], the questions remain the same as those raised in [2]: how is it possible that a very long lived molecule of a 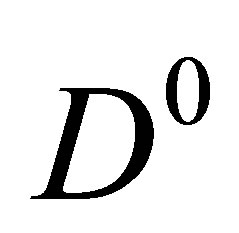 and a
and a 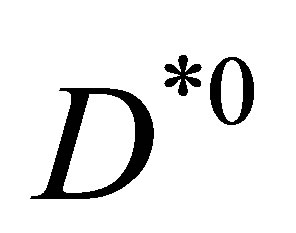 meson, with binding energy compatible with zero, could be formed within the bulk of the hadrons ejected in very high energy
meson, with binding energy compatible with zero, could be formed within the bulk of the hadrons ejected in very high energy 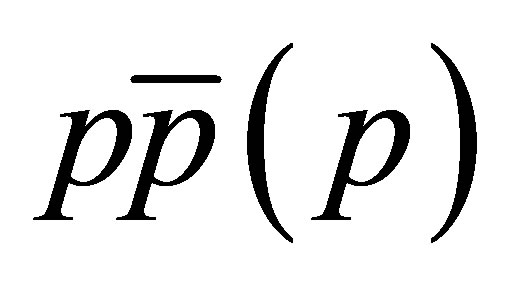 collisions? Is it the
collisions? Is it the 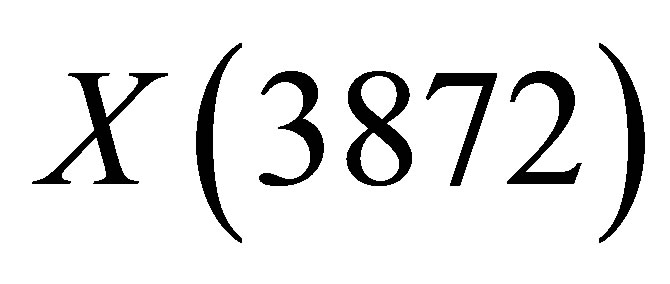 that molecule?
that molecule?
The reply given in [2] to the former question was sharply negative. In that paper, we performed numerical simulations with standard hadronization algorithms (Herwig and Pythia) tuned to fit data on the production of open charm mesons and sought 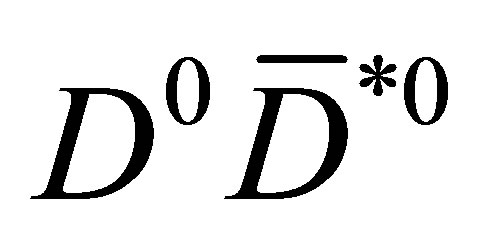 pairs with reasonably low relative momentum in their centre of mass so as to be eligible candidates for becoming molecular loosely bound states. The number of selected pairs allowed to estimate an upper bound on the prompt1 production cross section of the
pairs with reasonably low relative momentum in their centre of mass so as to be eligible candidates for becoming molecular loosely bound states. The number of selected pairs allowed to estimate an upper bound on the prompt1 production cross section of the 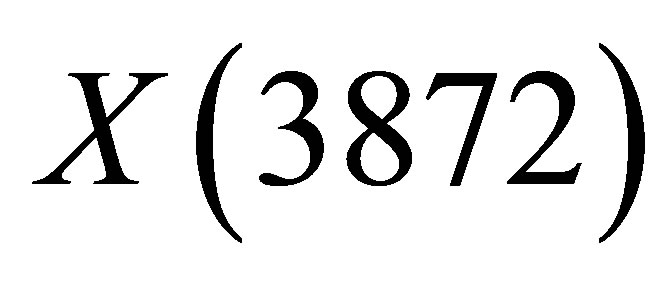 which was found to be at least 30 times smaller than the experimental value.
which was found to be at least 30 times smaller than the experimental value.
Our analysis was reproduced, with similar results, in [3], where it was also observed that a more appropriate treatment of Tevatron data would rather indicate a discrepancy with theoretical expectations by a factor of 300.
Such a gap did not seem to be unbridgeable to the authors of [3], who resorted to final state interaction (FSI) mechanisms in the 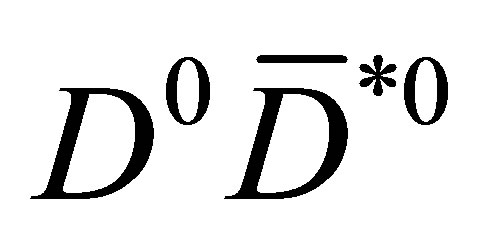 system in order to improve the theoretical cross section up to the experimental value. The approach there used was criticised in [4] leaving the controversy somewhat unsolved [5].
system in order to improve the theoretical cross section up to the experimental value. The approach there used was criticised in [4] leaving the controversy somewhat unsolved [5].
2. Molecular 
On the other hand, during the last few years, the idea of a molecular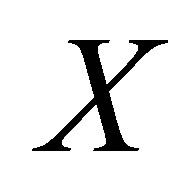 , in diverse incarnations [6-13], has been corroborated by the lack of observation of its nearly degenerate charged partners, required by the antagonist tetraquark model [14]. For these reasons we come back here to the problem of the
, in diverse incarnations [6-13], has been corroborated by the lack of observation of its nearly degenerate charged partners, required by the antagonist tetraquark model [14]. For these reasons we come back here to the problem of the 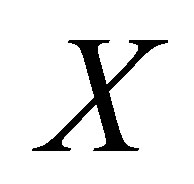 formation in high energy hadron collisions being motivated by a completely different approach. In our view the
formation in high energy hadron collisions being motivated by a completely different approach. In our view the  could rather be the meson-molecule analogue of the stable deuterium.
could rather be the meson-molecule analogue of the stable deuterium.
Given the large number of pions produced in the neighbourhood of the open charm meson pairs in momentum phase space, it is plausible that some of those pions could scatter elastically on the 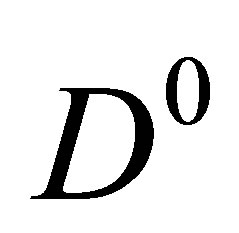 or
or 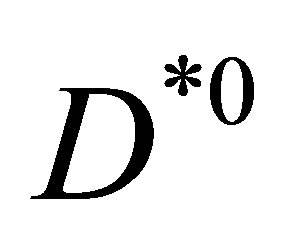 component of the would-be-molecule changing the relative momentum in the centre of mass of the pair,
component of the would-be-molecule changing the relative momentum in the centre of mass of the pair, 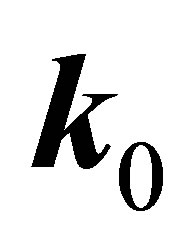 , towards lower values—see Figure 1. We can assume the initial total energy
, towards lower values—see Figure 1. We can assume the initial total energy  of the pair to be positive. However, if
of the pair to be positive. However, if 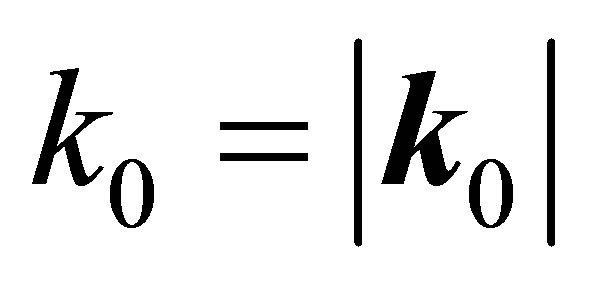 gets smaller due to an interaction with the pion,
gets smaller due to an interaction with the pion,  might be found shifted down to some negative— close to zero—value, provided that the
might be found shifted down to some negative— close to zero—value, provided that the 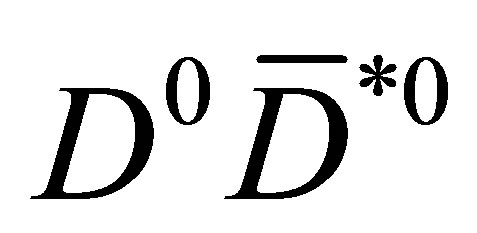 pair is under the influence of some (unknown) attractive potential, say a square well potential, similar to the simplest description of deuterium.
pair is under the influence of some (unknown) attractive potential, say a square well potential, similar to the simplest description of deuterium.
In these respects the 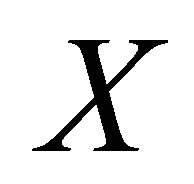 would be a genuine, negative energy, bound state of
would be a genuine, negative energy, bound state of 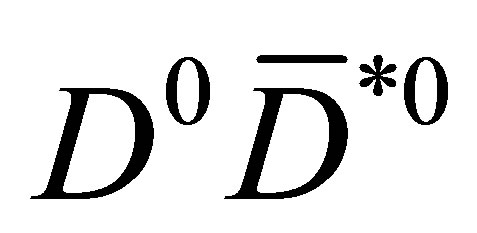 whose lifetime is entirely regulated by the lifetime of the shorter lived component
whose lifetime is entirely regulated by the lifetime of the shorter lived component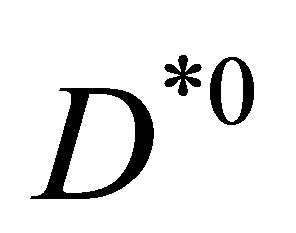 ; we would estimate then a total width
; we would estimate then a total width 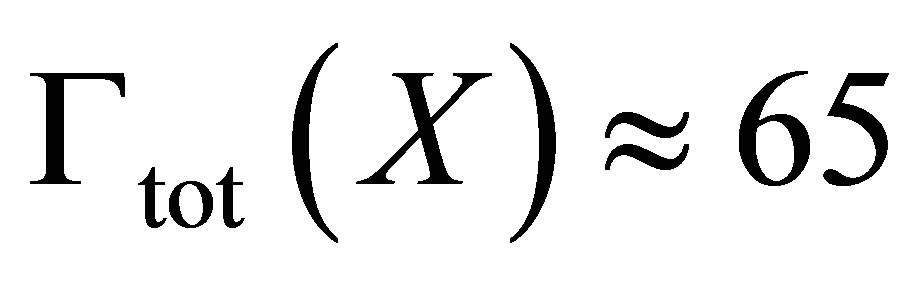 keV [15]. There are no energetic arguments to stabilize the
keV [15]. There are no energetic arguments to stabilize the  in the attractive potential.
in the attractive potential.
Such a mechanism is therefore somewhat opposite to the one based on FSI, where the 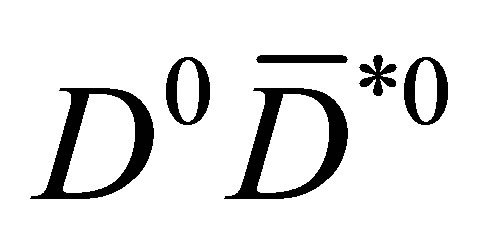 pair should rescatter remaining isolated from other hadrons potentially produced close in phase space [3,4]. One more reason to pursue the approach described above is that the resonant scattering
pair should rescatter remaining isolated from other hadrons potentially produced close in phase space [3,4]. One more reason to pursue the approach described above is that the resonant scattering 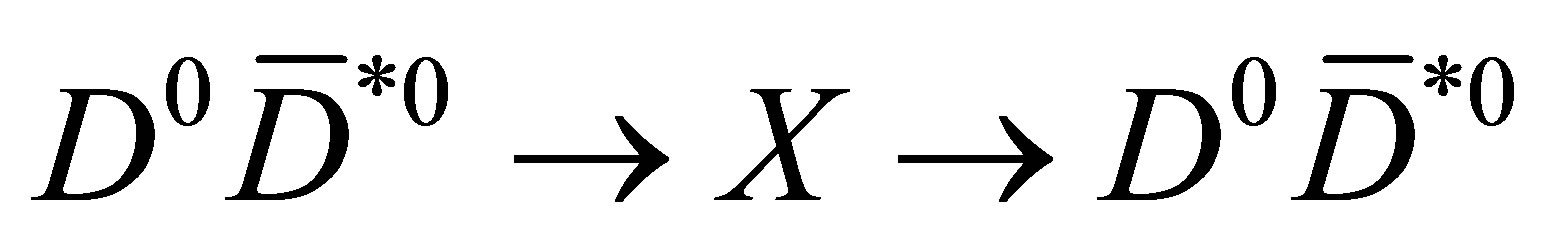 is difficult to be reconciled with the general expectations that can be drawn for the total scattering cross section of two particles allowing a shallow bound state with energy
is difficult to be reconciled with the general expectations that can be drawn for the total scattering cross section of two particles allowing a shallow bound state with energy 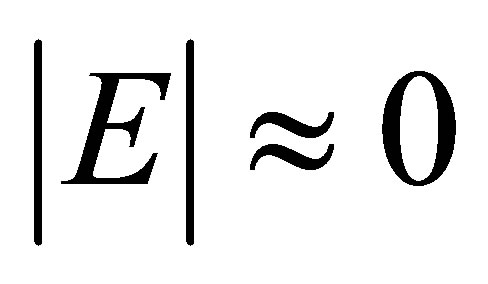 , as described in the “Low equation” formalism, see [16]. Resonant scattering
, as described in the “Low equation” formalism, see [16]. Resonant scattering 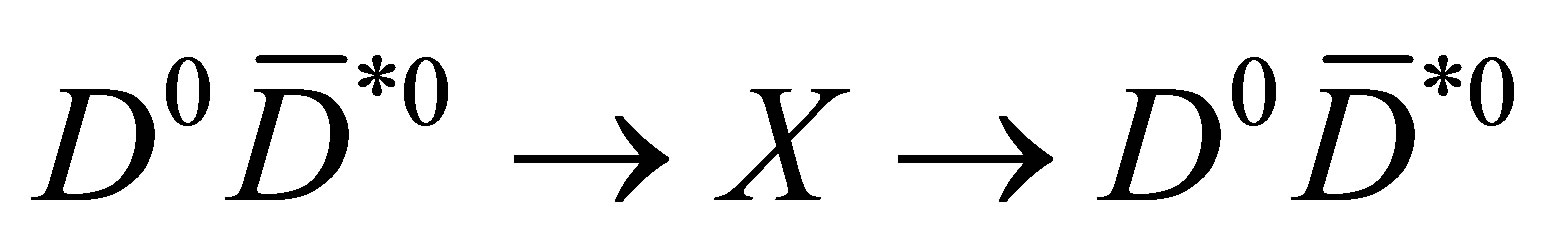 can be computed using available data on
can be computed using available data on 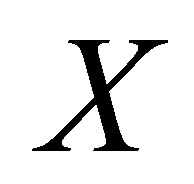 decay branching fractions (in order to compute the
decay branching fractions (in order to compute the 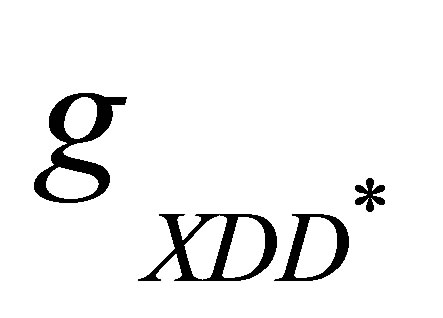 coupling) and averaging the cross section,
coupling) and averaging the cross section,  , with the distribution
, with the distribution
 of
of  pairs obtained by hadronization algorithms2. It is only when
pairs obtained by hadronization algorithms2. It is only when  is smaller than some critical value
is smaller than some critical value  that the resonant scattering into
that the resonant scattering into  has a non negligible probability to occur. We find a scattering legth
has a non negligible probability to occur. We find a scattering legth  of about 4 fm for a total width
of about 4 fm for a total width
 MeV (the
MeV (the  coupling is a function of the
coupling is a function of the 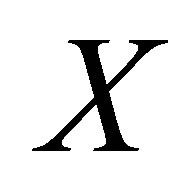 total width) and
total width) and 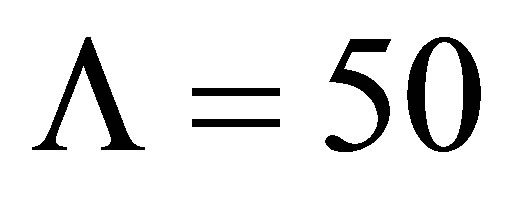 MeV. The scattering length
MeV. The scattering length  decreases for smaller values of the total width—see Figure 2. Shifting
decreases for smaller values of the total width—see Figure 2. Shifting  towards higher values,
towards higher values,  GeV,
GeV,  decreases to few cents of a fermi.
decreases to few cents of a fermi.
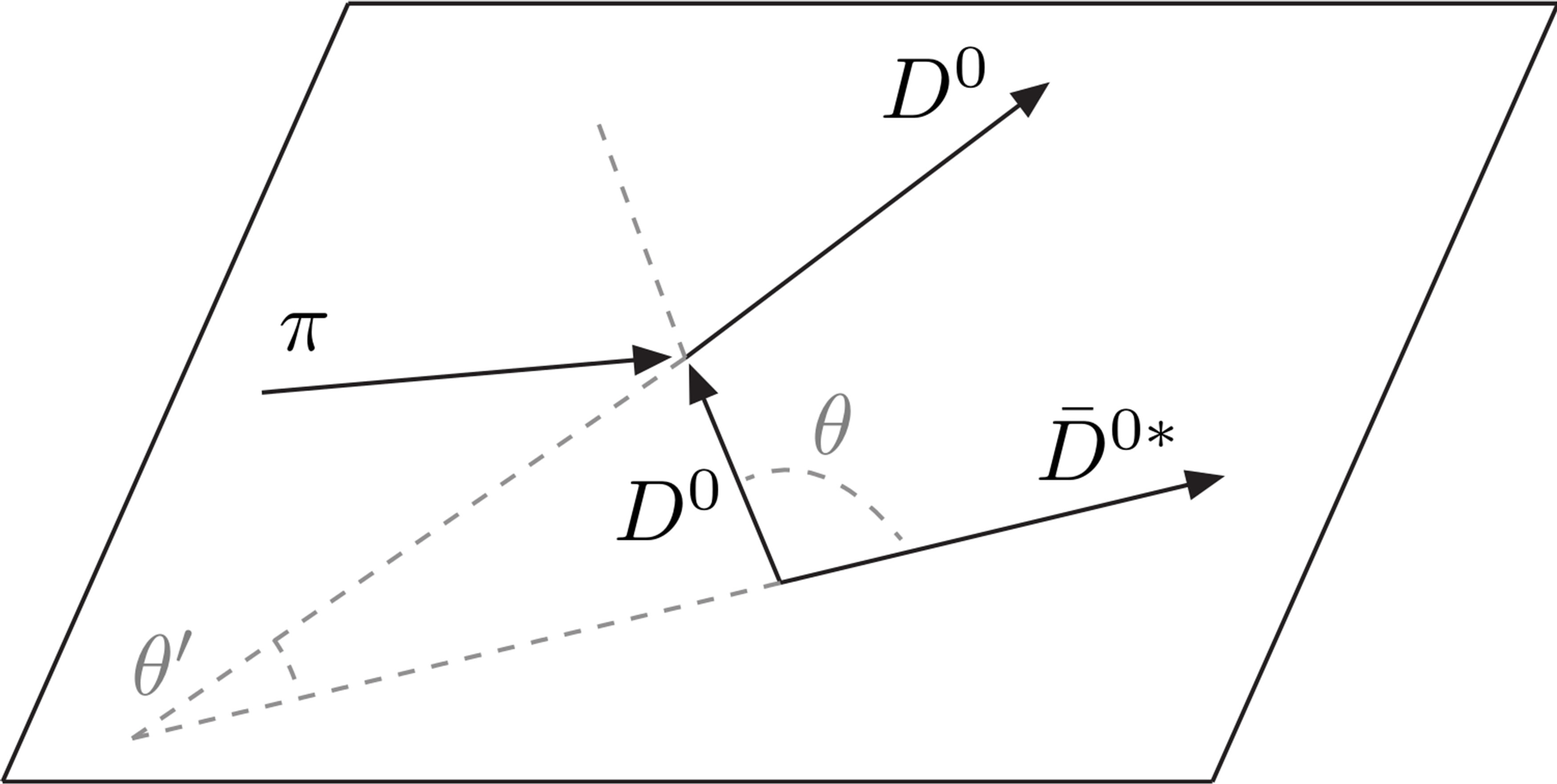
Figure 1. The elastic scattering of a 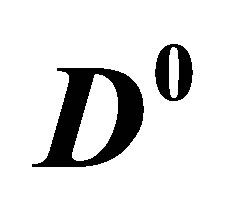 (or
(or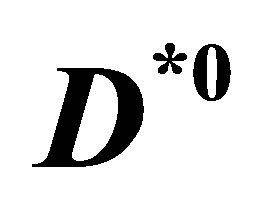 ) with a pion among those produced in hadronization could reduce the relative momentum
) with a pion among those produced in hadronization could reduce the relative momentum 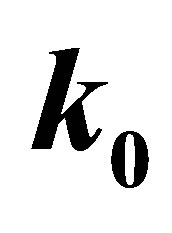 in the centre of mass of the
in the centre of mass of the 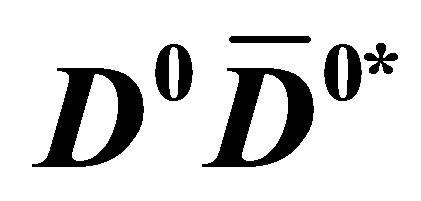 pair.
pair.
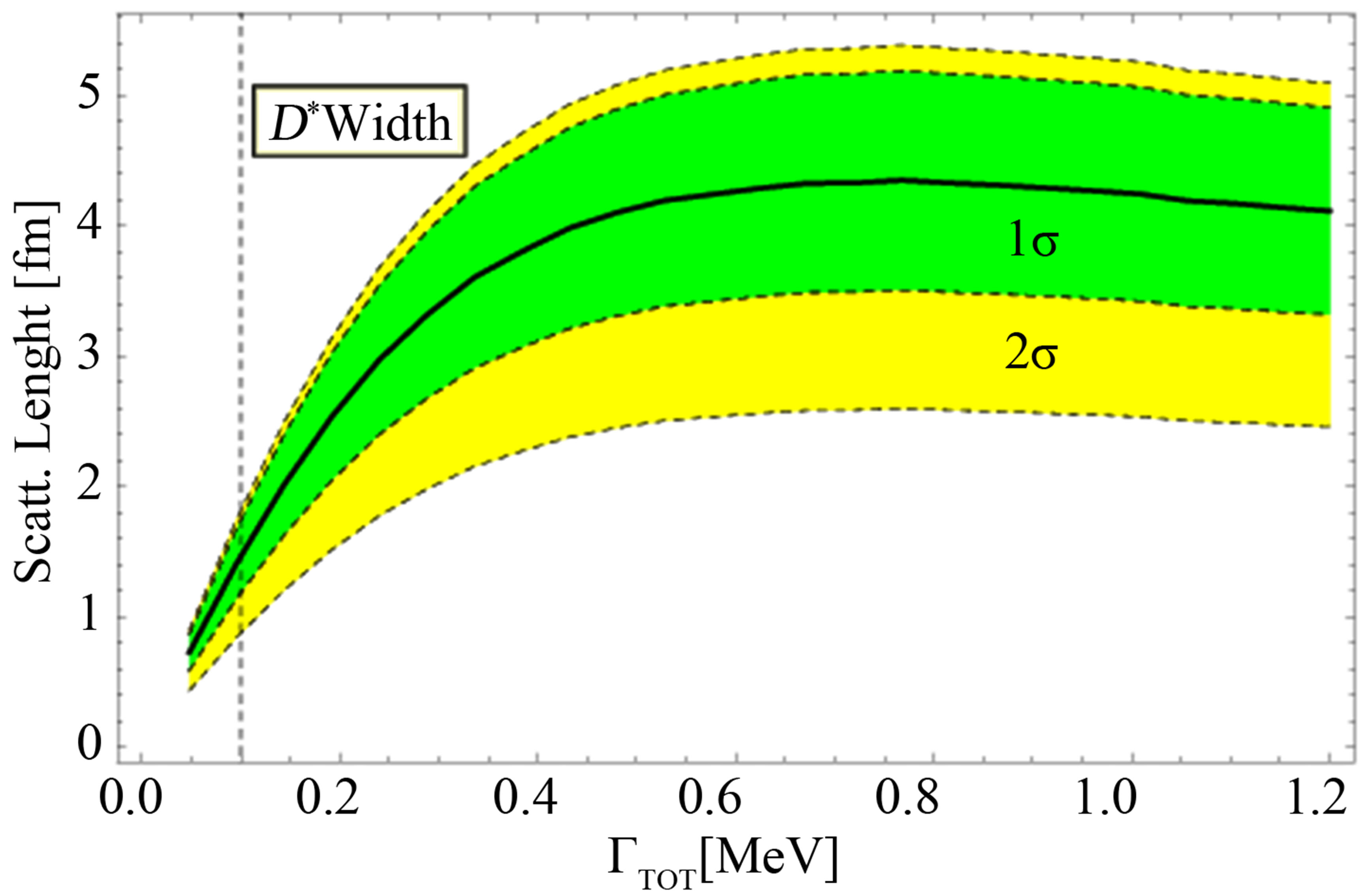
Figure 2. Scattering length for the 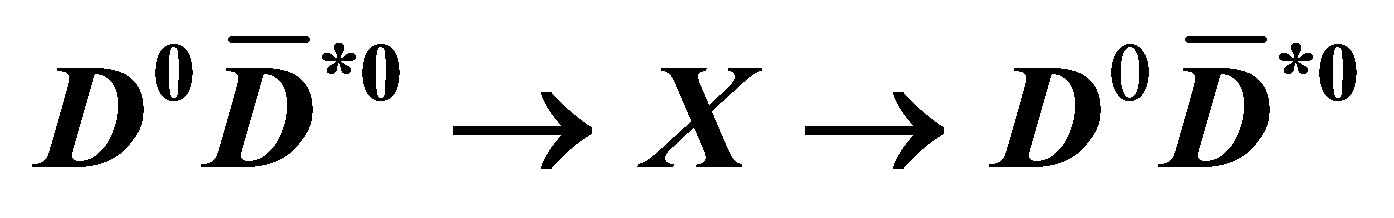 process as a function of the
process as a function of the  total width. The initial pairs are selected with
total width. The initial pairs are selected with 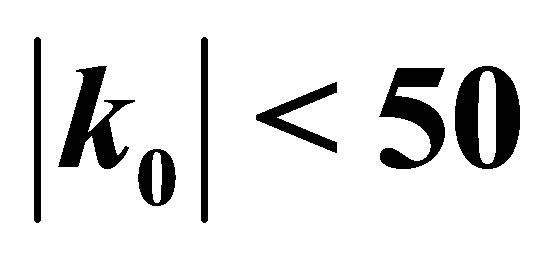 MeV which, in our simulations, represent a few parts over
MeV which, in our simulations, represent a few parts over  of the total. The error bands account for uncertainties on the data we used.
of the total. The error bands account for uncertainties on the data we used.
On the other hand, the scattering length expected for scattering with a shallow bound state is 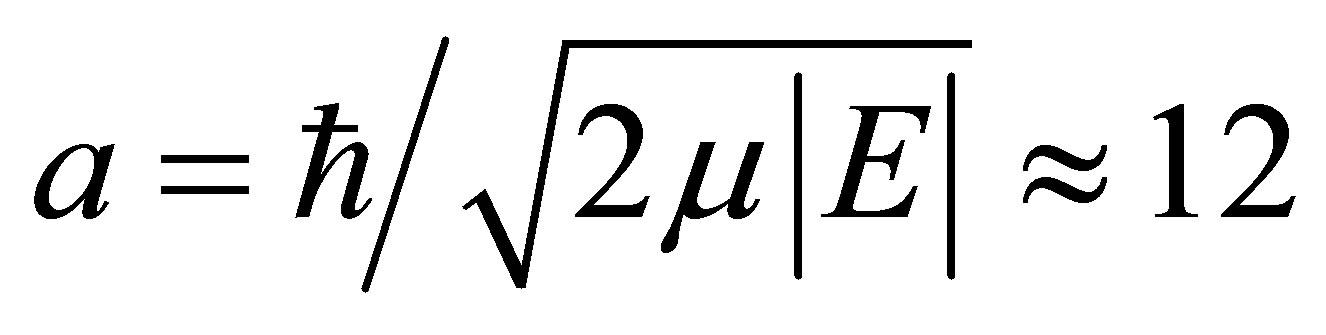 fm (
fm (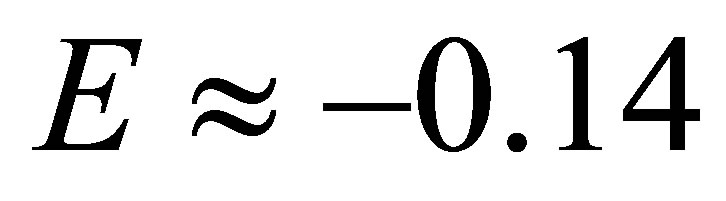 MeV). Such a result, as discussed in [16], is independent on the (unknown) scattering potential.
MeV). Such a result, as discussed in [16], is independent on the (unknown) scattering potential.
3. Analysis Method
The binding energy of the 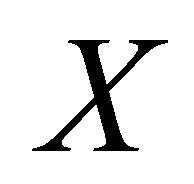 is estimated from the mass difference with its constituents
is estimated from the mass difference with its constituents  MeV. A discrete level at this energy (take the central value) can be accommodated in a square well with a depth of about
MeV. A discrete level at this energy (take the central value) can be accommodated in a square well with a depth of about 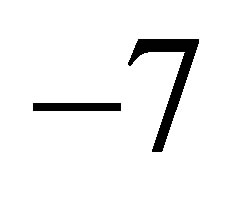 MeV3 and a range
MeV3 and a range 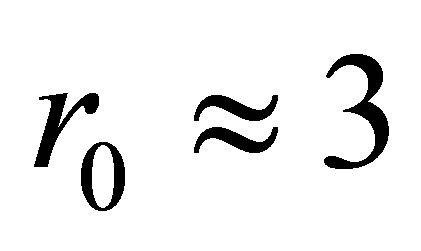 fm.
fm.
Let 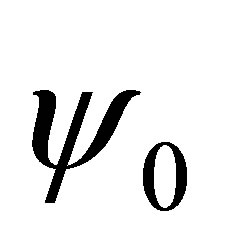 be the wave function associated to this level. The average size of the molecule is found to be
be the wave function associated to this level. The average size of the molecule is found to be
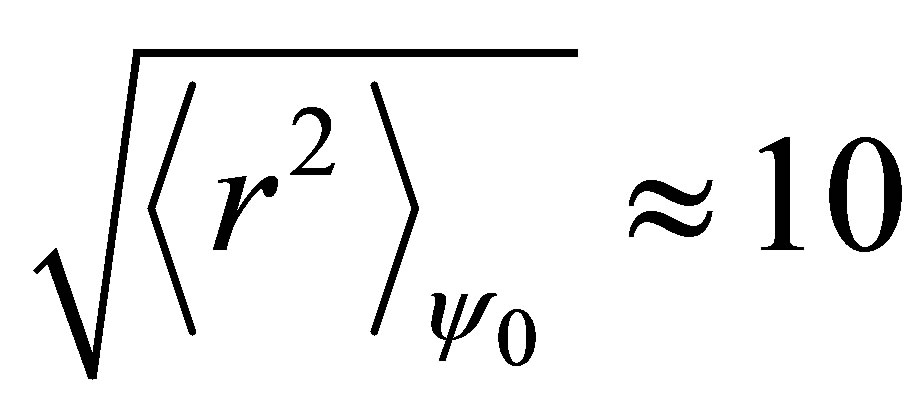 fm and a value of
fm and a value of 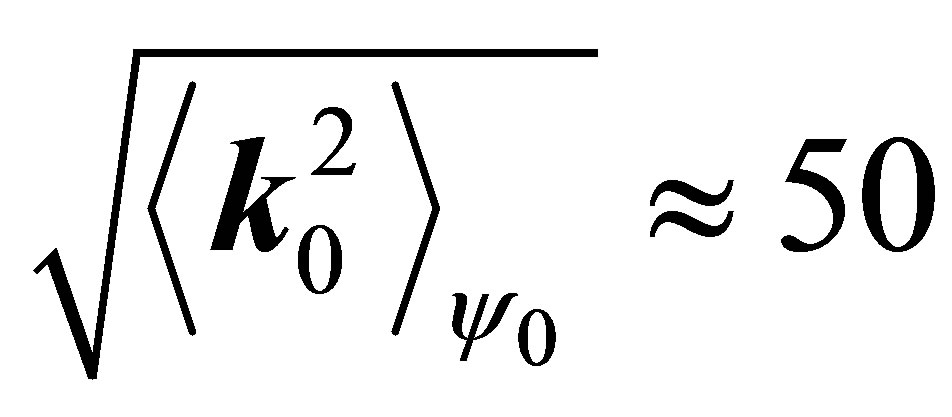 MeV is determined. Those pions scattering elastically on
MeV is determined. Those pions scattering elastically on 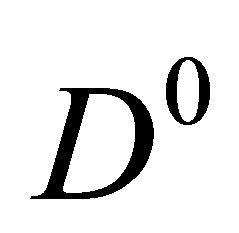 or
or 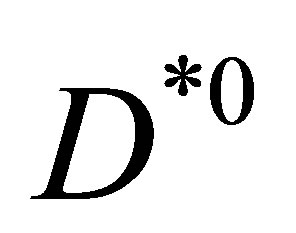 and making the
and making the 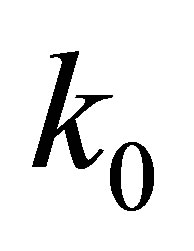 of the pair lower than 50 MeV are able to drop the total energy down to
of the pair lower than 50 MeV are able to drop the total energy down to  and form a genuine
and form a genuine 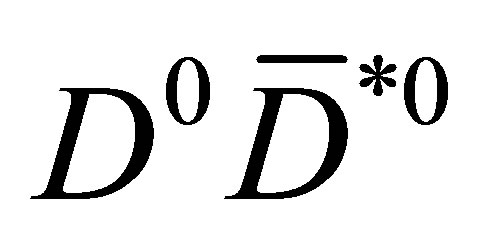 bound state. It is our purpose here to seek such pions and to study numerically their elastic interactions with the
bound state. It is our purpose here to seek such pions and to study numerically their elastic interactions with the 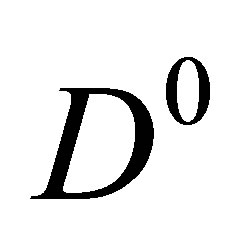 or
or 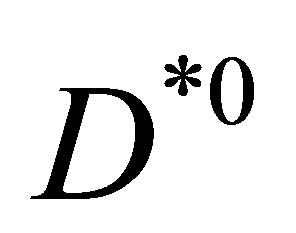 mesons adapting standard hadronization tools such as Herwig and Pythia.
mesons adapting standard hadronization tools such as Herwig and Pythia.
As discussed first in [2], the spectrum of 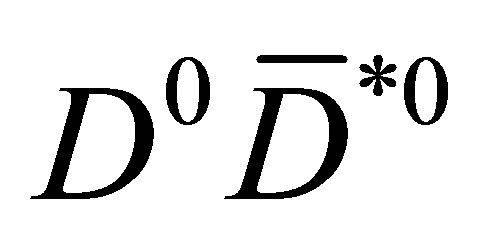 pairs can be represented by a monotonically rising histogram in
pairs can be represented by a monotonically rising histogram in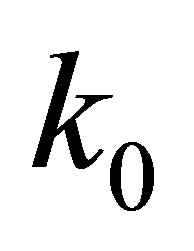 . Because of the interaction with pions, pairs with high relative COM (centre of mass) momenta, the majority, could either be pushed to higher momenta or to lower ones. If even a small part of them were rearranged within lower relative momenta, there could be a significant effect of feed-down of pairs towards lower bins, even in the far low energy region below 50 MeV. Populating that region means increasing the formation probability of the loosely bound
. Because of the interaction with pions, pairs with high relative COM (centre of mass) momenta, the majority, could either be pushed to higher momenta or to lower ones. If even a small part of them were rearranged within lower relative momenta, there could be a significant effect of feed-down of pairs towards lower bins, even in the far low energy region below 50 MeV. Populating that region means increasing the formation probability of the loosely bound .
.
To perform a first qualitative exploration of this phenomenon, we start by generating samples of 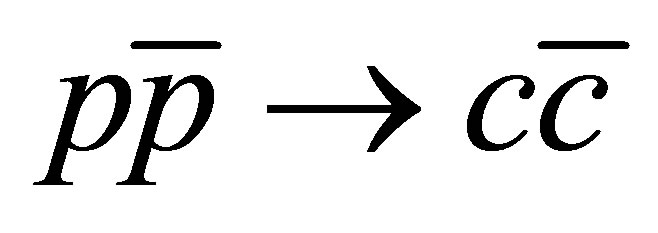 events in Herwig and Pythia, at Tevatron COM energies (
events in Herwig and Pythia, at Tevatron COM energies (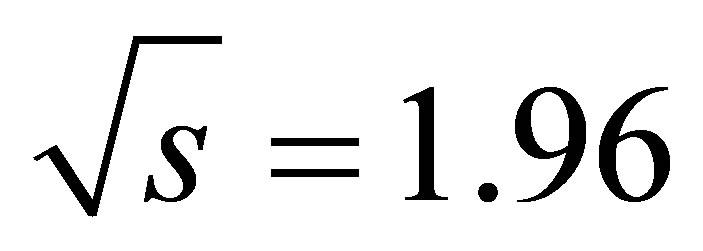 TeV). We list the events containing
TeV). We list the events containing 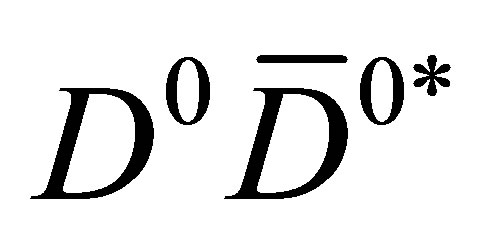 (resp.
(resp.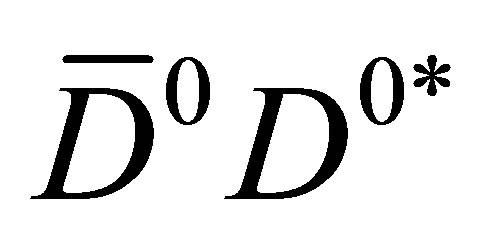 ) as a function of
) as a function of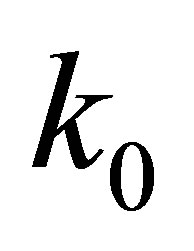 . The cuts imposed at parton level are:
. The cuts imposed at parton level are: 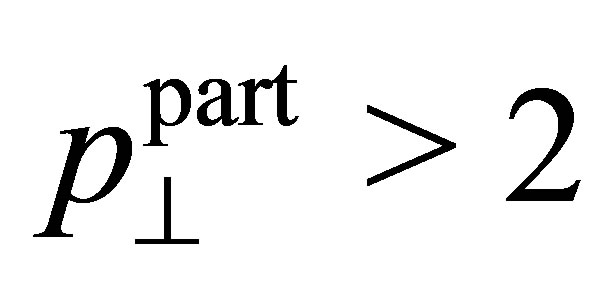 GeV and
GeV and .
.
The distributions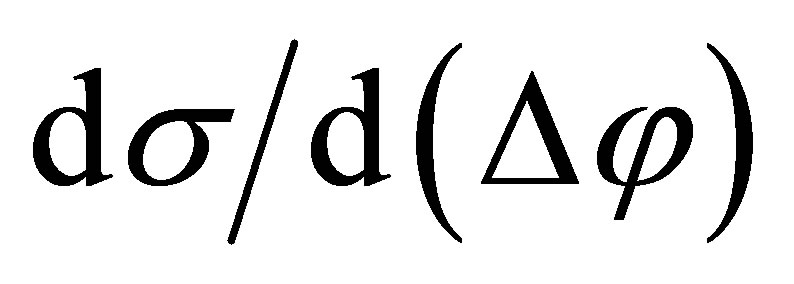 , where
, where 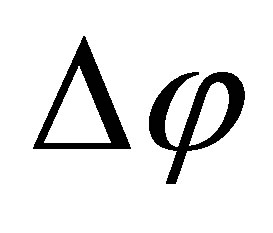 is the difference in azimuthal angles between
is the difference in azimuthal angles between  and
and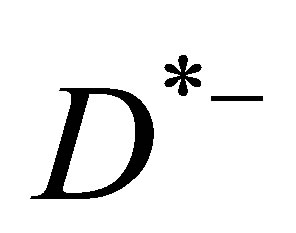 , as discussed in [2], are reproduced by choosing the following cuts on the final mesons: open charm meson pairs have
, as discussed in [2], are reproduced by choosing the following cuts on the final mesons: open charm meson pairs have 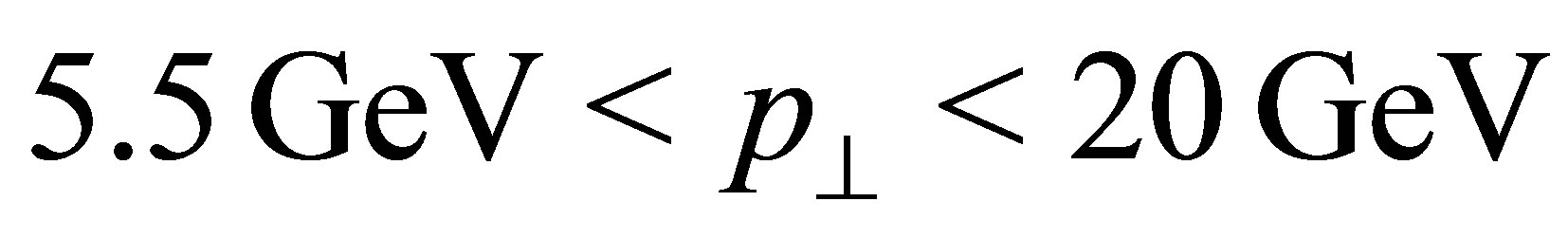 and
and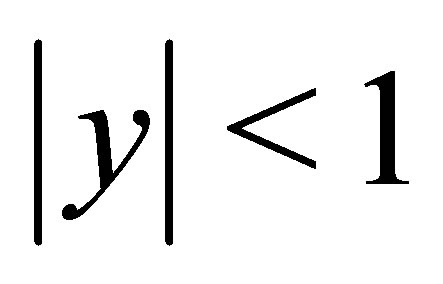 . These cuts allow to reproduce very well CDF data on
. These cuts allow to reproduce very well CDF data on  if a full Quantum Chromodynamics (QCD) generation of events is performed
if a full Quantum Chromodynamics (QCD) generation of events is performed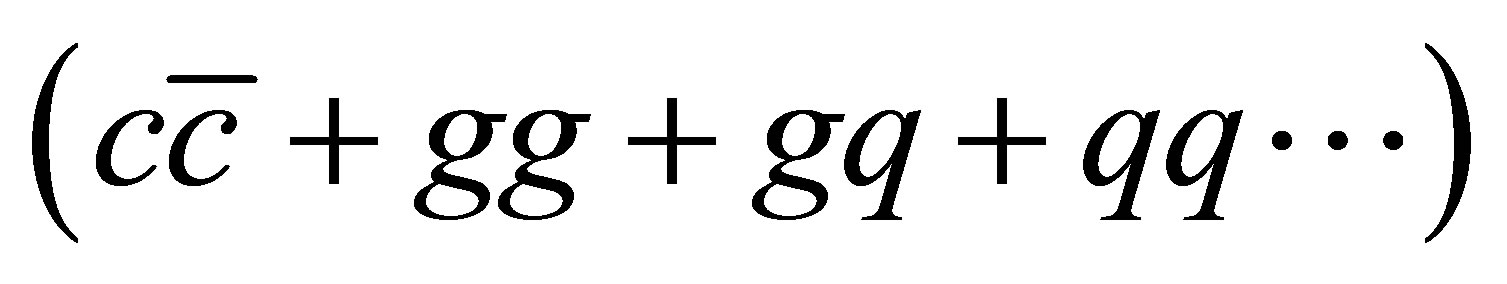 .
. 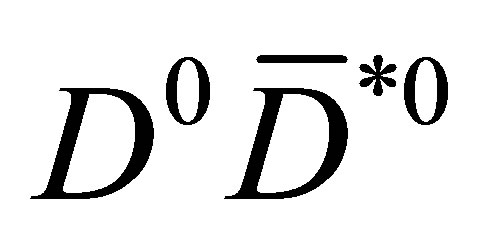 pairs in the bin
pairs in the bin 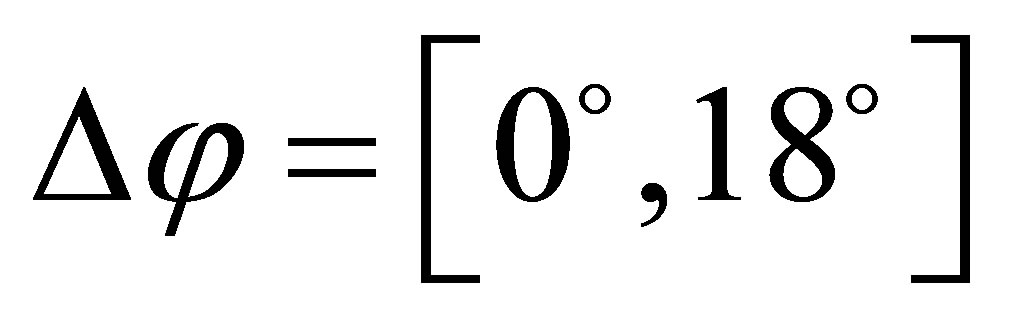 are the main would-be-molecule candidates. We observe here that the numerical generation of
are the main would-be-molecule candidates. We observe here that the numerical generation of 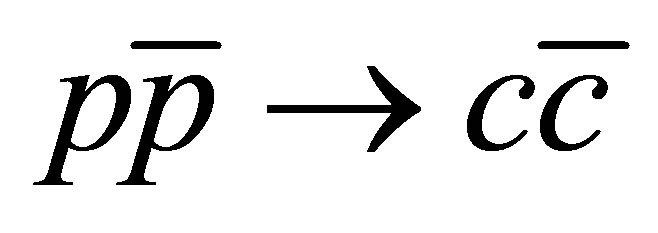 partially fills
partially fills 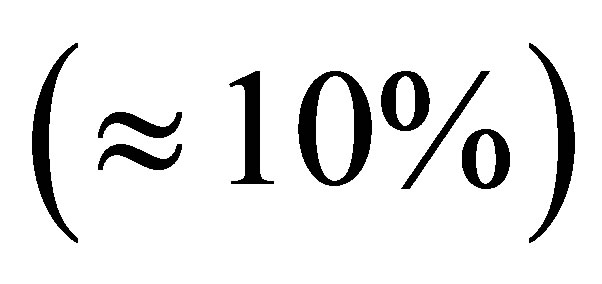 the
the  bin with respect to the full QCD one. In addition, in the central region, which is enforced by the cuts, we have to match our results with those of some Matrix Element Monte Carlo, like Alpgen [17], more than just using shower algorithms. We will present the results of the full QCD simulation, which is much more time consuming, in a future paper.
bin with respect to the full QCD one. In addition, in the central region, which is enforced by the cuts, we have to match our results with those of some Matrix Element Monte Carlo, like Alpgen [17], more than just using shower algorithms. We will present the results of the full QCD simulation, which is much more time consuming, in a future paper.
To optimize the selection of events, we choose the 10 most complanar pions to the 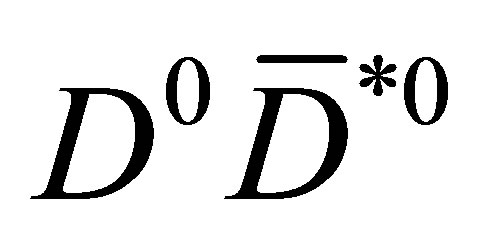 plane, then we randomly choose the meson the pion will interact with (say the
plane, then we randomly choose the meson the pion will interact with (say the ), and finally we select the most parallel pion to the non-interacting meson (say the
), and finally we select the most parallel pion to the non-interacting meson (say the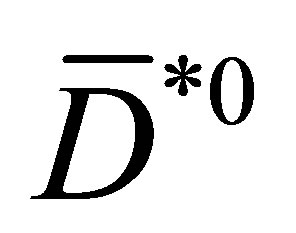 )—see Figure 1. In physical events, we expect such a pion to be the most effective one to the phenomenon we are describing.
)—see Figure 1. In physical events, we expect such a pion to be the most effective one to the phenomenon we are describing.
The elastic interactions with the pions are regulated in the 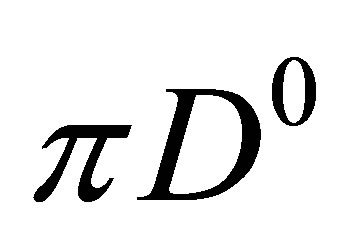 COM by the matrix elements
COM by the matrix elements
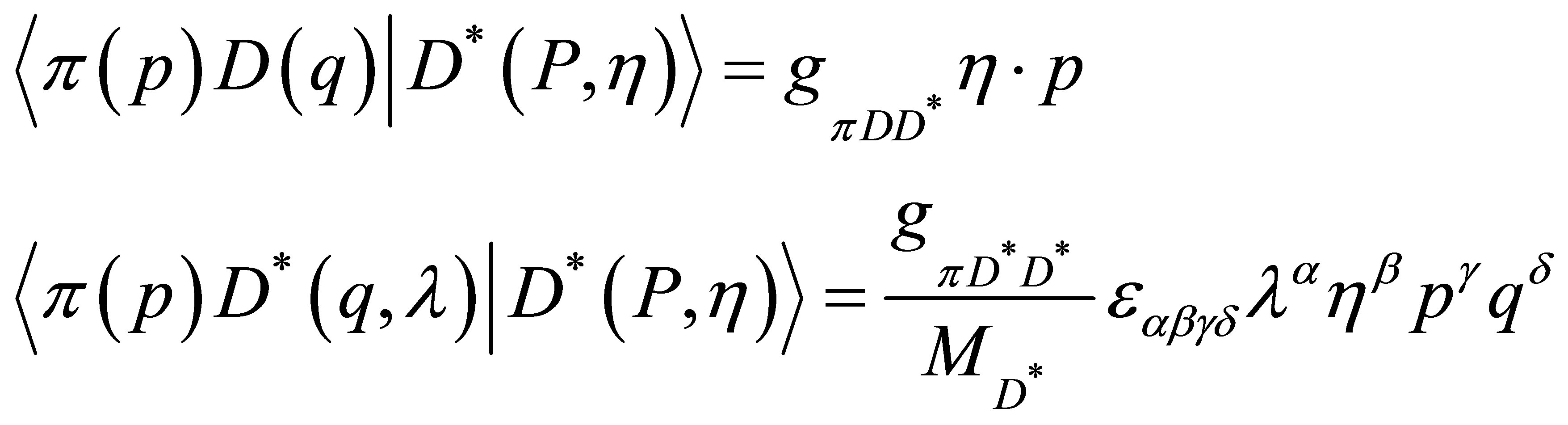
where the couplings used are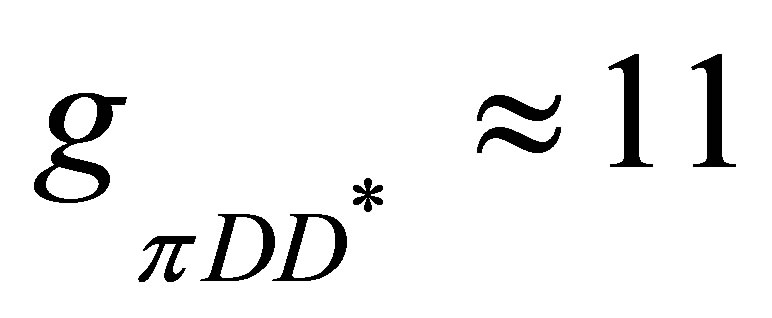 ,
, 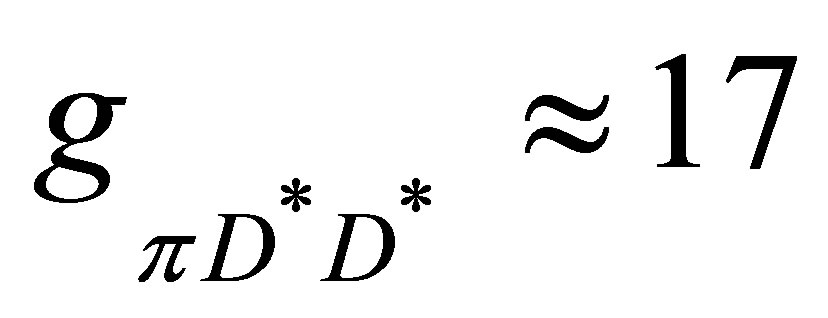 see [18-20]. After the interaction with the pion has taken place in the COM
see [18-20]. After the interaction with the pion has taken place in the COM  frame, we boost back the
frame, we boost back the  in the laboratory (LAB) frame and check if the “new”
in the laboratory (LAB) frame and check if the “new” 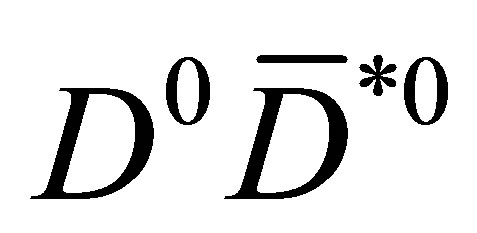 pair passes the cuts we fixed for the final meson pairs.
pair passes the cuts we fixed for the final meson pairs.
We can trace, event by event, the variation  of each
of each 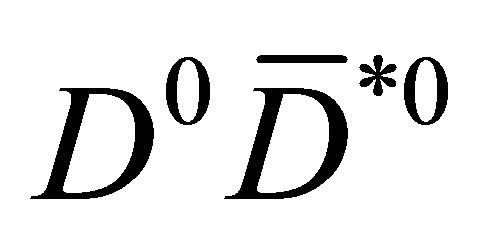 pair filling a 2D histogram of transition probabilities
pair filling a 2D histogram of transition probabilities . Since the interaction with pions can change the
. Since the interaction with pions can change the 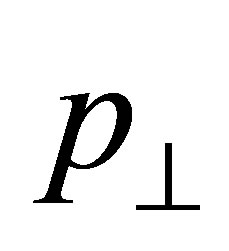 and
and 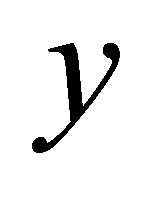 of the molecule, a pair might fail the strict meson cuts before the interaction and pass them after it (a “gained” would-be-molecule) and viceversa (a “lost” one): see Figure 3.
of the molecule, a pair might fail the strict meson cuts before the interaction and pass them after it (a “gained” would-be-molecule) and viceversa (a “lost” one): see Figure 3.
The open charm mesons might interact with pions more than once before a molecule is formed. Roughly speaking the  scattering is proportional to
scattering is proportional to
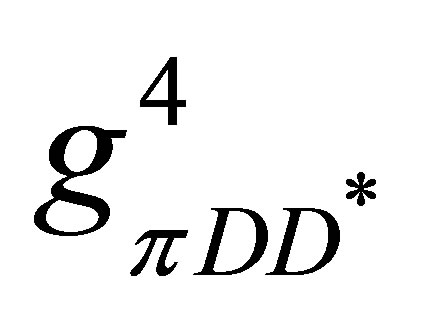 whereas the
whereas the 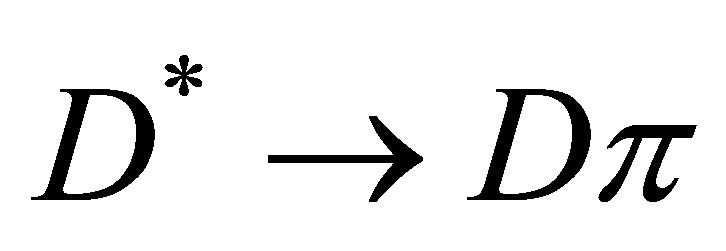 decay is “slower” by
decay is “slower” by
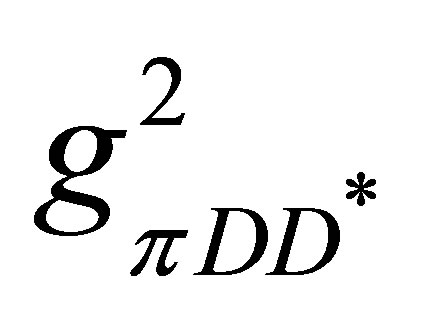 4. We assume that a single
4. We assume that a single 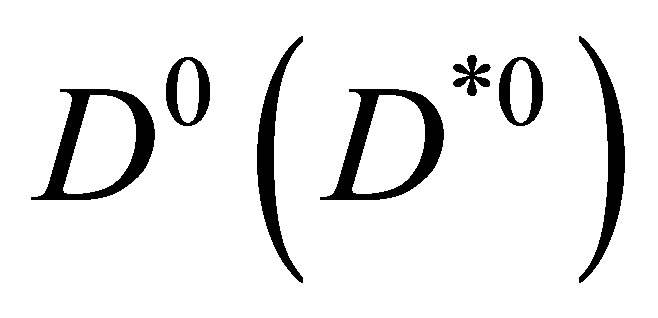 might
might
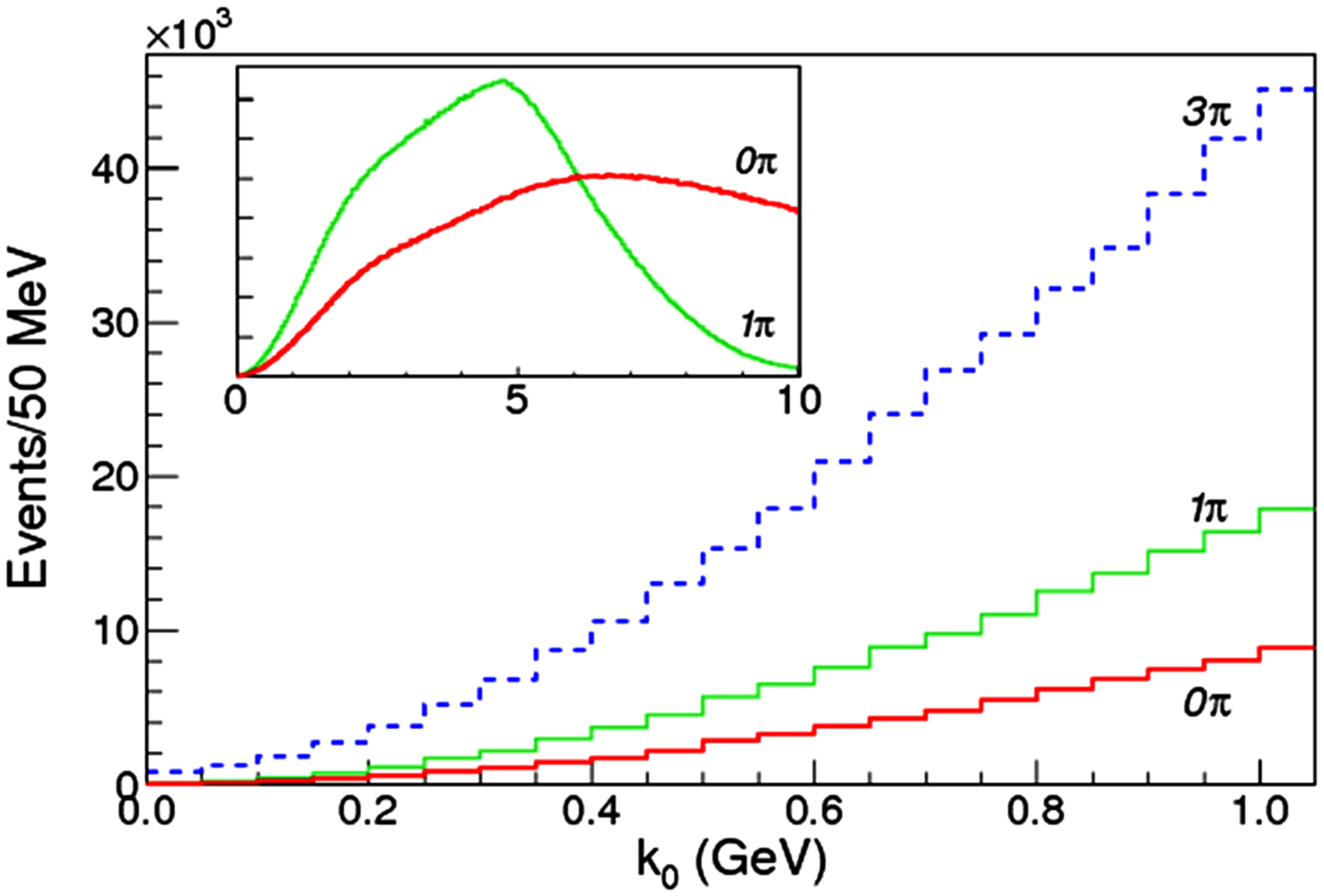
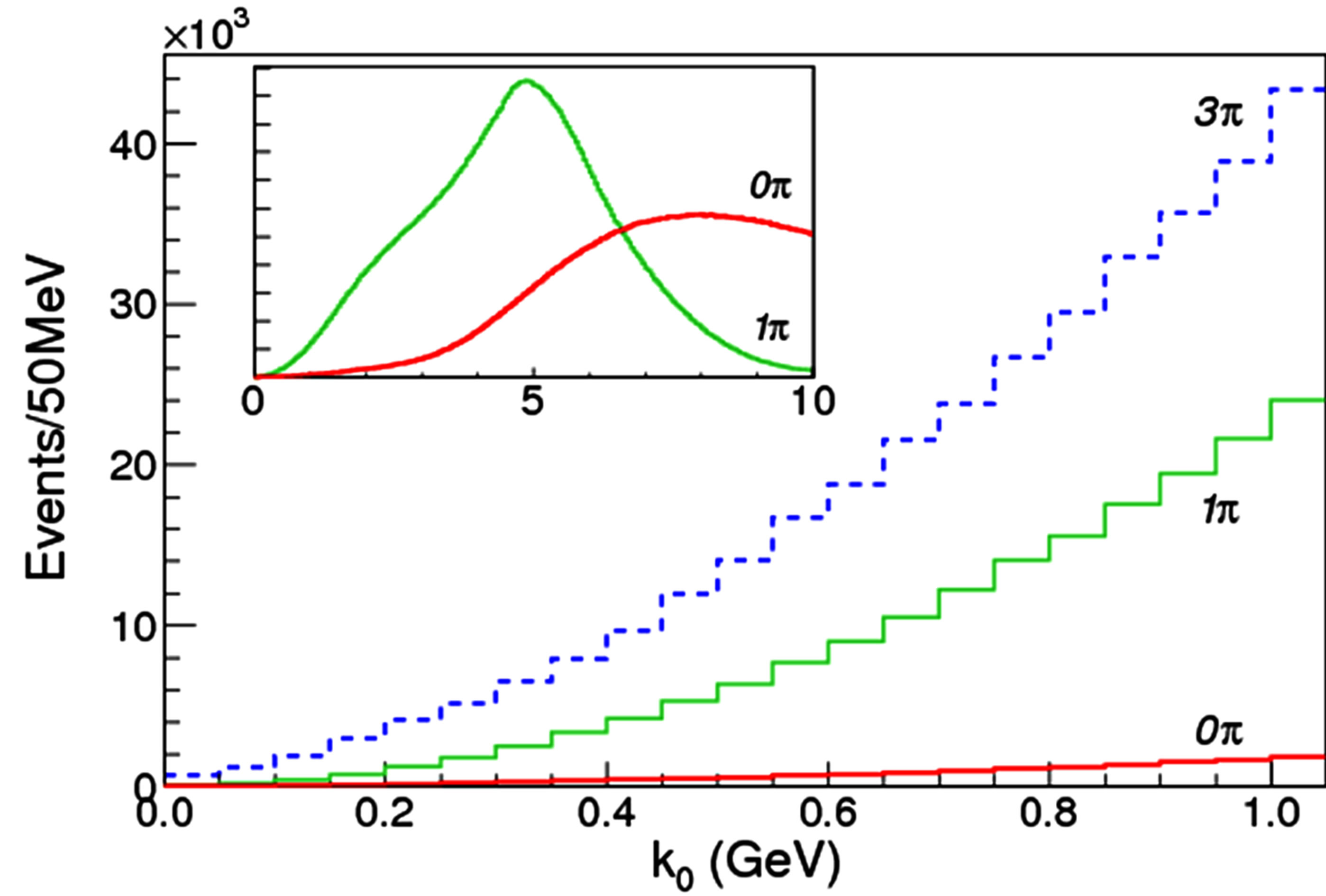
Figure 3. Number of 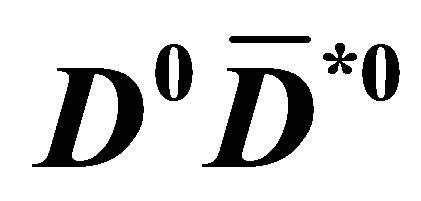 pairs (events) counted with Herwig (upper panel) and Pythia (lower panel) when generating
pairs (events) counted with Herwig (upper panel) and Pythia (lower panel) when generating 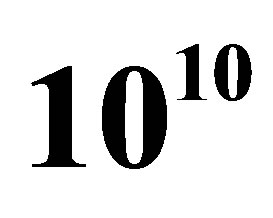
 events at
events at 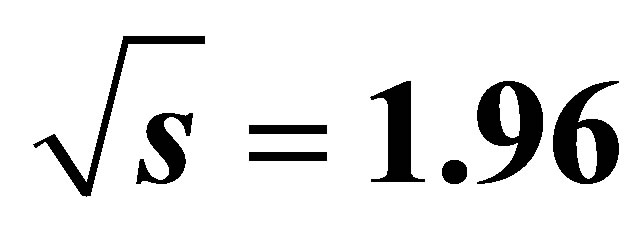 TeV with the cuts on partons and hadrons described in the text. The
TeV with the cuts on partons and hadrons described in the text. The  histogram reproduces the shape found in [2]. The histograms named
histogram reproduces the shape found in [2]. The histograms named  and
and  are related to the elastic scattering of open charm mesons with one or three pions selected as described above. In the insects we report a broader
are related to the elastic scattering of open charm mesons with one or three pions selected as described above. In the insects we report a broader 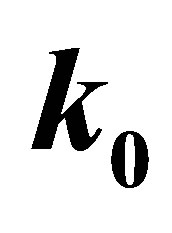 range.
range.
scatter, on average, with 2 - 3 pions before the relative distances among the flying-out hadrons are such that the interactions are suppressed5.
Therefore, for each pair, we wish to evaluate 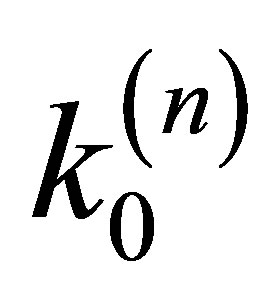 after n interactions. We do it according to the probability distribution functions (PDF) as extracted from
after n interactions. We do it according to the probability distribution functions (PDF) as extracted from 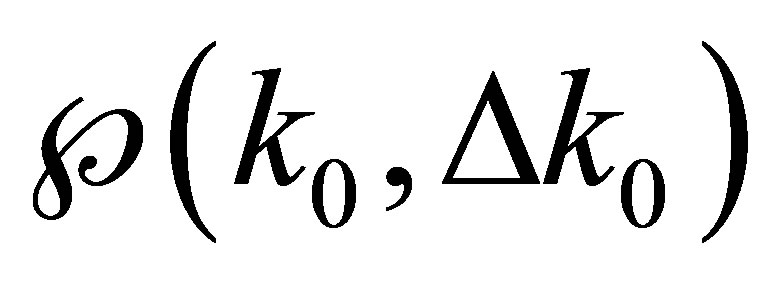 . We build a set of PDFs
. We build a set of PDFs 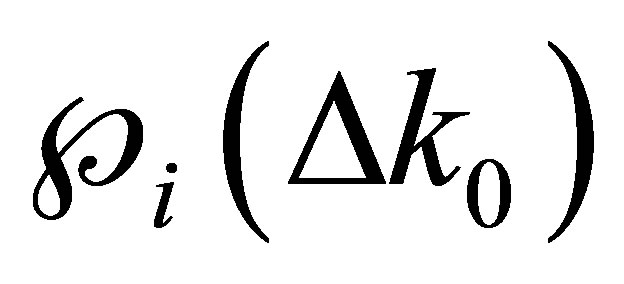 for each bin
for each bin  in
in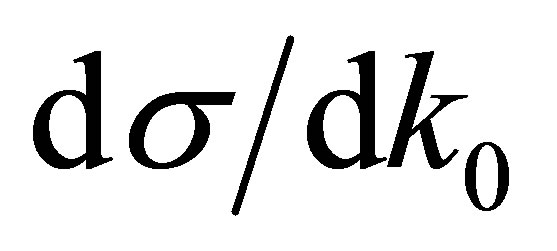 . We assume that the PDFs will be the same for all the interactions, like in a Markov chain. For each event we have a
. We assume that the PDFs will be the same for all the interactions, like in a Markov chain. For each event we have a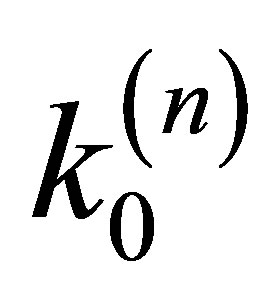 , falling in some particular bin
, falling in some particular bin . We randomly extract a
. We randomly extract a  according to the distribution
according to the distribution 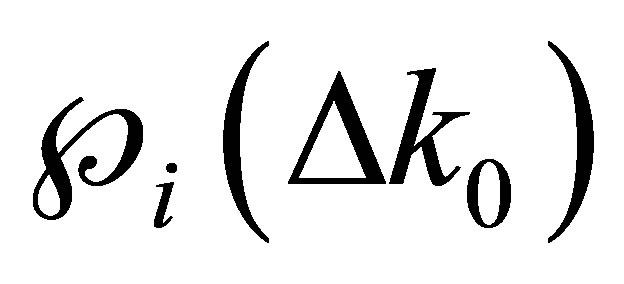 and sum
and sum 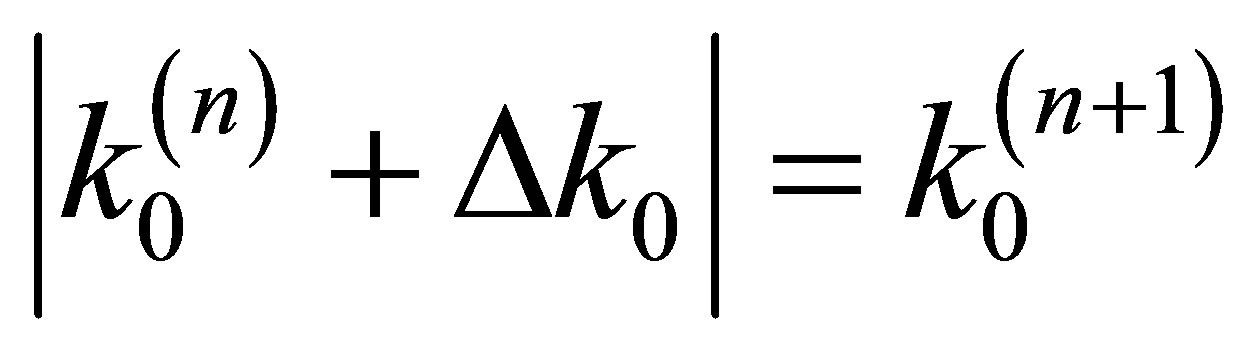 thus producing a new histogram.
thus producing a new histogram.
We must also take into account the “lost” and “gained” would-be-molecules. In each iteration, we generate the number of “lost” and “gained” ones, 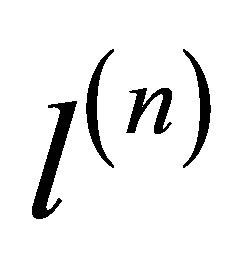 ,
, 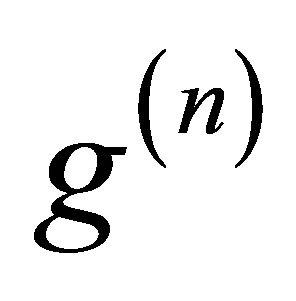 , according to Poissonian distributions with mean values
, according to Poissonian distributions with mean values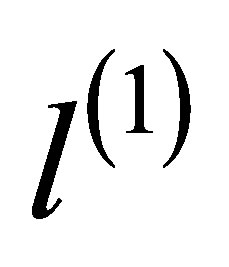 ,
,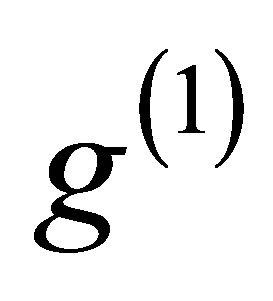 . We implement the following algorithm: 1) before the
. We implement the following algorithm: 1) before the 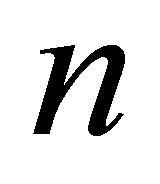 -th interaction, we drop out a number
-th interaction, we drop out a number  of pairs, 2) we produce the new histogram as a result of the interaction with one more pion, 3) after that, we decide to “gain” a
of pairs, 2) we produce the new histogram as a result of the interaction with one more pion, 3) after that, we decide to “gain” a 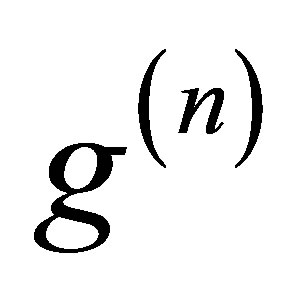 number of pairs.
number of pairs.
4. Results
The results are showed in Figure 3. The bin we are more interested in is the first one, with 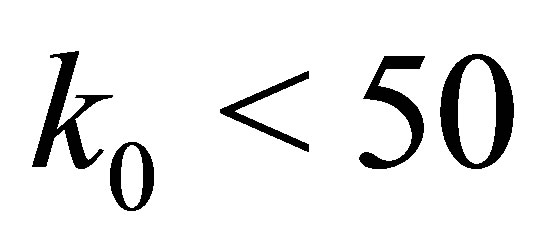 MeV. The number of pairs obtained for that bin are reported in Table 1.
MeV. The number of pairs obtained for that bin are reported in Table 1.
As one can see from these plots the feed-down mechanism towards lower relative momentum bins is very effective once the interaction of a 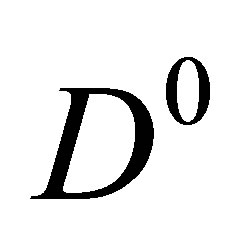 or a
or a 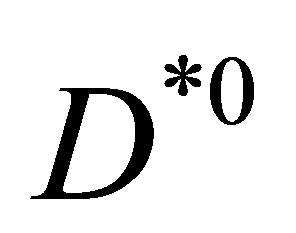 with a pion from the hadronization is taken into account. The effect gets magnified if successive interactions are allowed (up to three). In the insects we show a broader range in
with a pion from the hadronization is taken into account. The effect gets magnified if successive interactions are allowed (up to three). In the insects we show a broader range in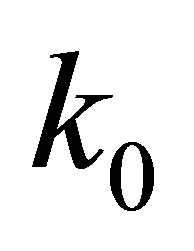 . It is evident here that the elastic scattering with a pion is also causing a net increase of would-bemolecule pairs: it forces a number of pairs to pass the
. It is evident here that the elastic scattering with a pion is also causing a net increase of would-bemolecule pairs: it forces a number of pairs to pass the 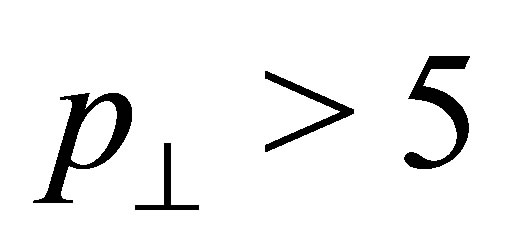 GeV and
GeV and  cuts, which otherwise would be failed.
cuts, which otherwise would be failed.
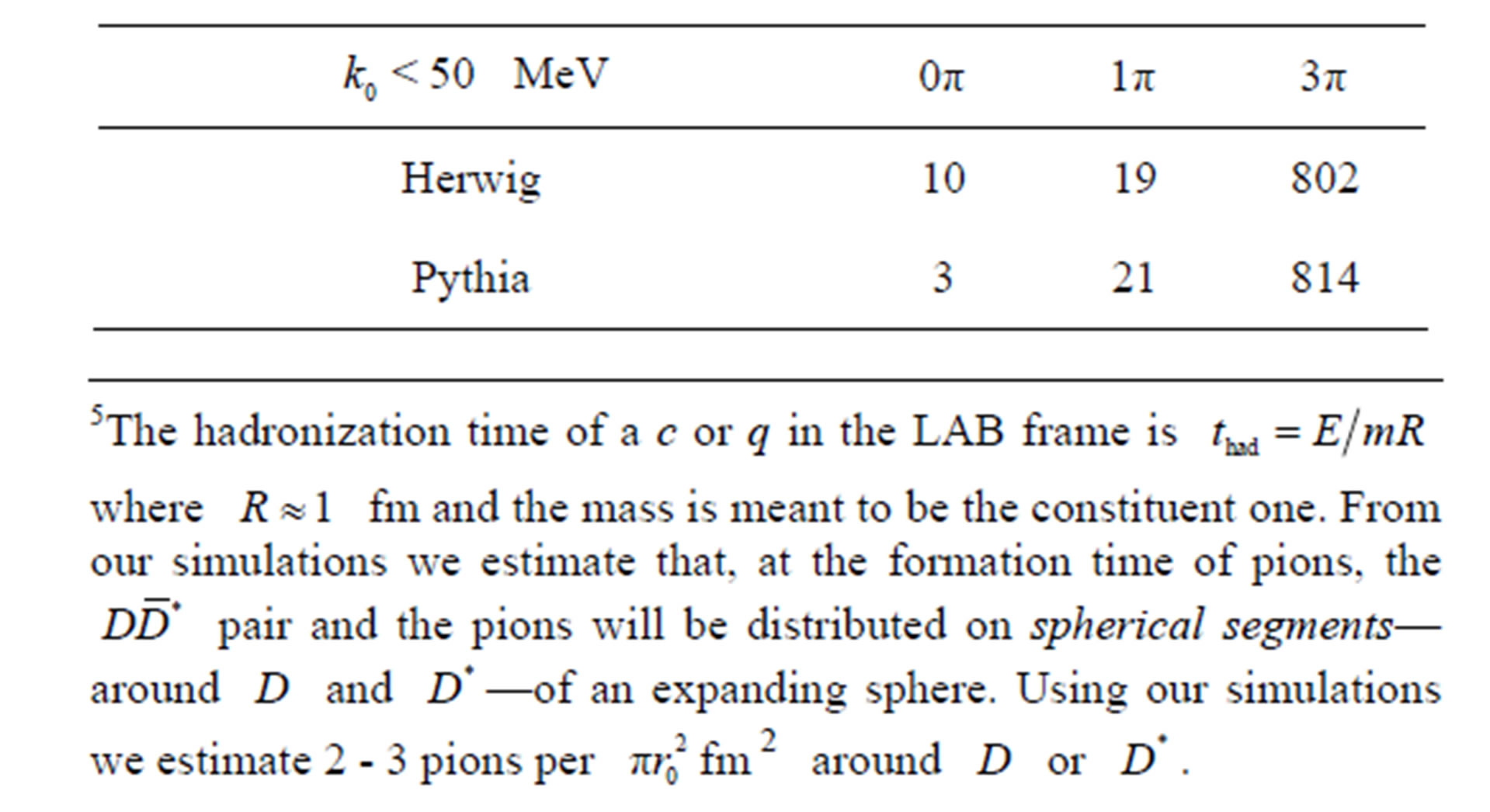
Table 1. The population of the the 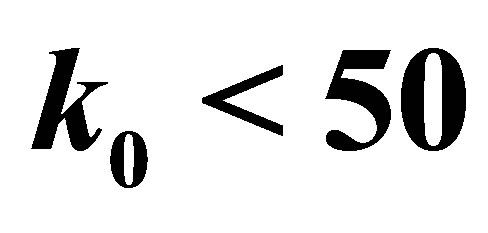 MeV bin (
MeV bin (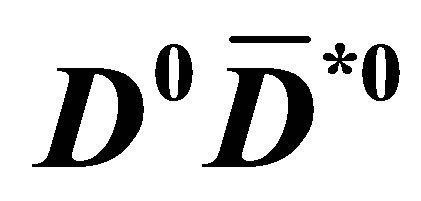 pairs), after
pairs), after ,
,  interactions.
interactions.
The results showed in Table 1 are indicating qualitatively that the mechanism described in this letter indeed occurs in numerical simulations of 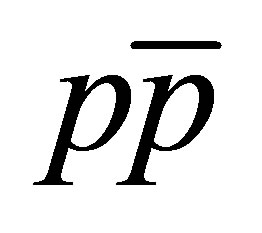 collisions and might play an important role in physical events. For a full determination of prompt production cross sections we need to switch from
collisions and might play an important role in physical events. For a full determination of prompt production cross sections we need to switch from 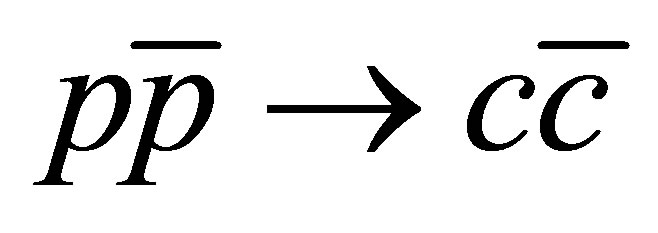 to the full QCD generation
to the full QCD generation 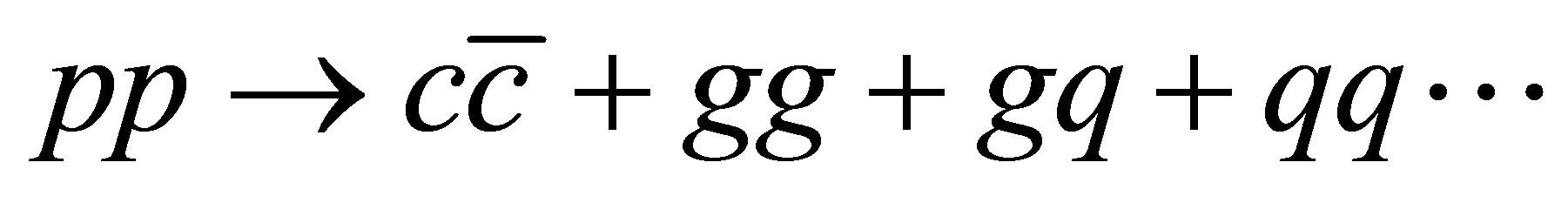 which is a harder task in terms of numerical computation, yet, from the exploration here reported, we have a clear clue on what to expect.
which is a harder task in terms of numerical computation, yet, from the exploration here reported, we have a clear clue on what to expect.
5. Conclusions
We have presented a new mechanism to explain the prompt formation of loosely bound open charm meson molecules at hadron colliders as induced by elastic scattering with comoving pions. Simplified numerical simulations show that pions produced in hadronization might be effective at decresing the relative momentum in the center of mass of the 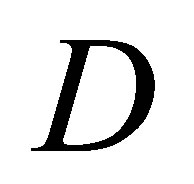 meson pair, if under the influence of an attractive potential, might therefore be found at some small negative energy, like in a shallow bound state in a potential well. Such a bound state will have a lifetime which is as long as the
meson pair, if under the influence of an attractive potential, might therefore be found at some small negative energy, like in a shallow bound state in a potential well. Such a bound state will have a lifetime which is as long as the  one,
one, 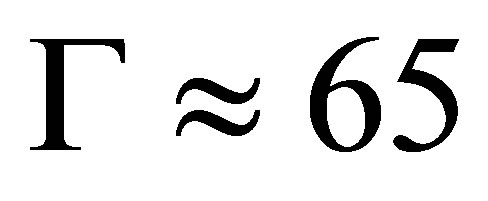 keV, still well below actual experimental resolution. With the results of the full numerical simulations, we will provide expected prompt cross sections for the production of the
keV, still well below actual experimental resolution. With the results of the full numerical simulations, we will provide expected prompt cross sections for the production of the 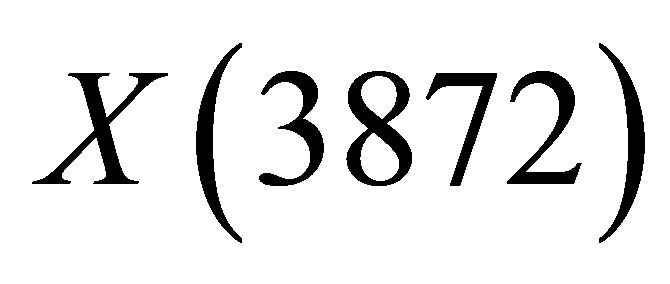 at the LHC.
at the LHC.
Considering the known limits of the available hadronization models, the results of numerical simulations have to be taken as compelling but qualitative descriptions of the suggested mechanism. We believe that several more investigations in this direction are possible.
6. Acknowledgements
A. P. thanks E. Braaten for stimulating discussion.
REFERENCES
- S. Chatrchyan, et al. Journal of High Energy Physics, Vol. 1304, 2013, p. 154. http://dx.doi.org/10.1007/JHEP04(2013)154
- C. Bignamini, B. Grinstein, F. Piccinini, A. D. Polosa and C. Sabelli, Physical Review Letters, Vol. 103, 2009, Article ID: 162001. http://dx.doi.org/10.1103/PhysRevLett.103.162001
- P. Artoisenet and E. Braaten, Physical Review Letters, Vol. D81, 2010, Article ID: 114018. http://dx.doi.org/10.1103/PhysRevLett.103.162001
- C. Bignamini, B. Grinstein, F. Piccinini, A. D. Polosa, V. Riquer and C. Sabelli, Physics Letters B, Vol. 684, 2010, pp. 228-230. http://dx.doi.org/10.1016/j.physletb.2010.01.037
- P. Artoisenet and E. Braaten, Physical Review D, Vol. 83, 2011, Article ID: 014019. http://dx.doi.org/10.1103/PhysRevD.83.014019
- F. E. Close and P. R. Page, Physics Letters B, Vol. 628, 2005, p. 215. http://dx.doi.org/10.1016/j.physletb.2005.09.016
- E. Braaten and M. Kusunoki, Physical Review D, Vol. 69, 2004, Article ID: 074005. http://dx.doi.org/10.1103/PhysRevD.69.074005
- F. E. Close and P. R. Page, Physics Letters B, Vol. 578, 2004, p. 119. http://dx.doi.org/10.1016/j.physletb.2003.10.032
- N. A. Tornqvist, Physics Letters B, Vol. 590, 2004, p. 209. http://dx.doi.org/10.1016/j.physletb.2004.03.077
- E. S. Swanson, Physics Reports, Vol. 429, 2006, p. 243. http://dx.doi.org/10.1016/j.physrep.2006.04.003
- S. Fleming, M. Kusunoki, T. Mehen and U. van Kolck, Physical Review D, Vol. 76, 2007, Article ID: 034006. http://dx.doi.org/10.1103/PhysRevD.76.034006
- E. Braaten and M. Lu, Physical Review D, Vol. 76, 2007, Article ID: 094028. http://dx.doi.org/10.1103/PhysRevD.76.094028
- E. Braaten and M. Lu, Physical Review D, Vol. 77, 2008, Article ID: 014029. http://dx.doi.org/10.1103/PhysRevD.77.014029
- L. Maiani, F. Piccinini, A. D. Polosa and V. Riquer, Physical Review D, Vol. 71, 2005, Article ID: 014028. http://dx.doi.org/10.1103/PhysRevD.71.014028
- E. Braaten and M. Lu, Physical Review D, Vol. 76, 2007, Article ID: 094028. http://dx.doi.org/10.1103/PhysRevD.76.094028
- S. Weinberg, “Lectures on Quantum Mechanichs,” Cambridge University Press, Cambridge, 2013.
- M. L. Mangano, M. Moretti, F. Piccinini, R. Pittau and A. D. Polosa, Journal of High Energy Physics, Vol. 0307, 2003. http://dx.doi.org/10.1088/1126-6708/2003/07/001
- R. Casalbuoni, A. Deandrea, N. Di Bartolomeo, R. Gatto, F. Feruglio and G. Nardulli, Physics Reports, Vol. 281, 1997, p. 145. http://dx.doi.org/10.1016/S0370-1573(96)00027-0
- A. Deandrea, N. Di Bartolomeo, R. Gatto, G. Nardulli and A. D. Polosa, Physical Review D, Vol. 58, 1998, Article ID: 034004. http://dx.doi.org/10.1103/PhysRevD.58.034004
- A. Deandrea, R. Gatto, G. Nardulli and A. D. Polosa, Physical Review D, Vol. 59, 1999, Article ID: 074012. http://dx.doi.org/10.1103/PhysRevD.59.074012
NOTES
*Corresponding author.
1i.e. not produced in B decays but at the hadron collision vertex.
2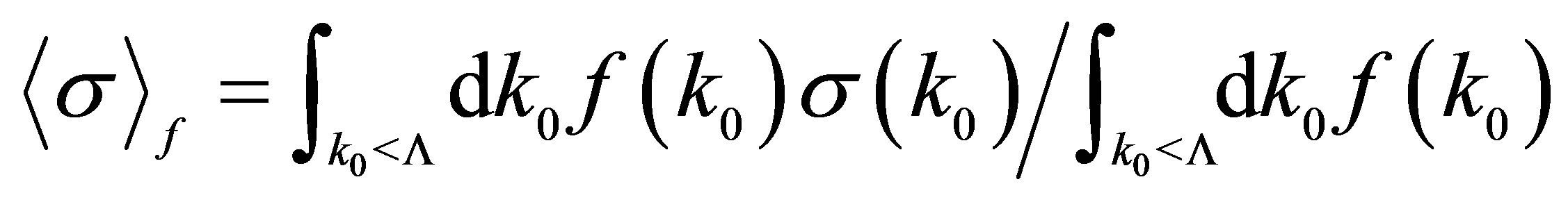
3–20 MeV in the case of deuterium.
4We might say that
 where we used the
where we used the  reduced mass for
reduced mass for . On the other hand
. On the other hand 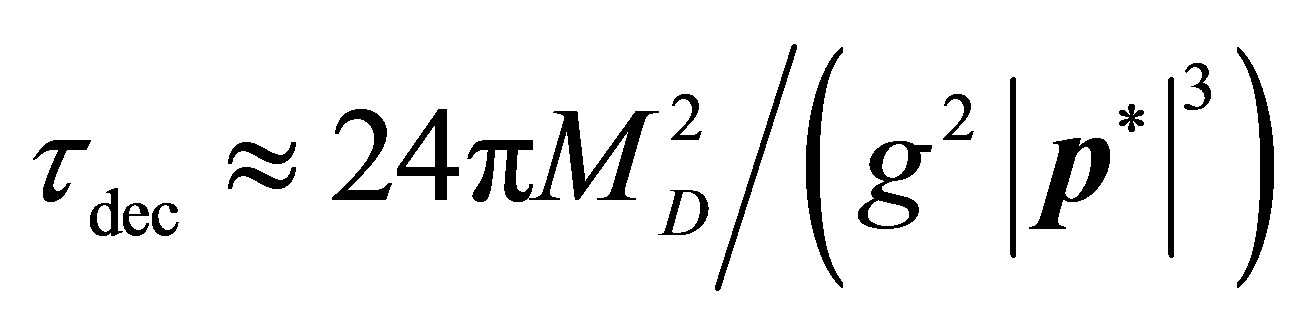 where
where  is the decay momentum. Thus
is the decay momentum. Thus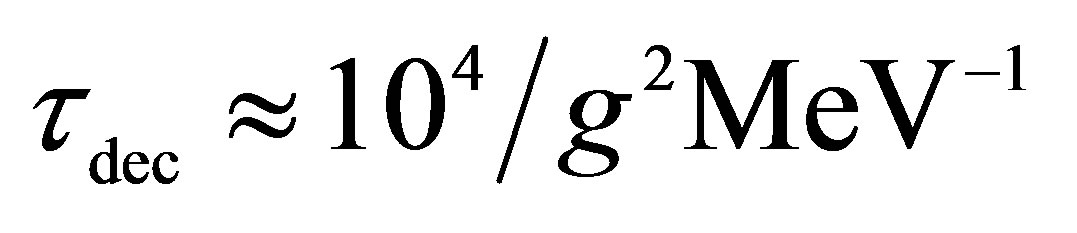 .
.

