Journal of Modern Physics
Vol.4 No.10A(2013), Article ID:38195,5 pages DOI:10.4236/jmp.2013.410A1003
Control of the Atomic Ionization with Short and Intense Chirped Laser Pulses
Laboratoire de Physique Computationnelle et Photonique, Université de Moncton Campus de Shippagan, Shippagan, Canada
Email: *samira.barmaki@umoncton.ca
Copyright © 2013 Samira Barmaki et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 3, 2013; revised September 5, 2013; accepted September 27, 2013
Keywords: Atomic System; Chirped Laser; Population Transfer; Nonperturbative Approach
ABSTRACT
We investigate a two-photon ionization process in a real hydrogen atom by short and intense chirped laser pulses. Our simulation of the laser-atom interaction consists on numerically solving the three-dimensional time-dependent Schrödinger equation with a spectral method. The unperturbed wave functions and electronic energies of the atomic system were found by using an accurate L2 discretisation technique based on the expansion of the wave functions on B-spline functions. We show the efficiency of chirped laser pulses to control the ionization yield and the transfer of the population to the 2p bound state involved in the ionization path.
1. Introduction
Thanks to the rapid advances in laser technology, laser pulses are becoming increasingly shorter and intense which make them an adequate tool to probe the ultrafast dynamics in atoms and molecules [1-5]. Experimentalists with theoreticians have worked consistently toward mastering the ionization control techniques by intense temporal pulses [6]. Depending on the characteristics of an incident laser pulse, different features could appear in the spectra of the emitted electrons or light from an atomic or a molecular system. Transform-limited pulses, which are ideal and bandwidth limited, have been extensively used to investigate laser-matter interaction [7]. A particular attention was given, in the past few years, to the effect of the carrier-phase envelope of a transform-limited pulse in controlling the ionization yield in some asymmetric molecular systems [8,9].
Recently, there is an increasing interest to investigate the interaction of atoms and molecules with chirped laser pulses [10-14]. These pulses that are frequency modulated have an advantage over unchirped laser pulses, i.e., transform-limited laser pulses. Their characterization and shaping make them more tailored to achieve complete electronic population inversion in molecular systems [15] and induce resonant multiphoton population transfer in Rydberg atoms [16-20]. It is important to note that the ability to control population transfer from an initial state to a desired final state is of crucial importance as it will open the way to the control of a chemical reaction’s end product.
In this paper, we show the efficiency of the chirped laser pulses to control the ionization yield in a real hydrogen atom. We used intense short chirped laser pulses of central carrier frequency 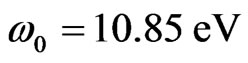 which correspond to the 7th harmonic of the Ti:Sapphire laser. A chirped laser pulse is experimentally produced by chirp filtering of a transform-limited laser pulse. We consider, in this paper, alistic experimental representation of a linearly polarized chirped laser pulse, in which the chirp parameter increases the pulse duration of the original transform-limited laser pulse and decreases its intensity. The frequency bandwidth of the resulting chirped pulse remains the same as that of the corresponding transform-limited laser pulse. The theoretical approach we used to calculate the unperturbed energetic structure of the hydrogen atom is based on an accurate L2 discretization technique using B-spline functions [21,22]. We calculated the ionization probability by numerically solving the three-dimensional time-dependent Schrödinger equation using a spectral method [23-25]. We show how the sign of the chirp parameter induces an asymmetry in the ionization process in the hydrogen atom. We present results of the time evolution of the 1s and 2p bound states population from the switch-on to the switch-off of the chirped pulses and then we analyze the role of the first excited state 2p in the ionization process.
which correspond to the 7th harmonic of the Ti:Sapphire laser. A chirped laser pulse is experimentally produced by chirp filtering of a transform-limited laser pulse. We consider, in this paper, alistic experimental representation of a linearly polarized chirped laser pulse, in which the chirp parameter increases the pulse duration of the original transform-limited laser pulse and decreases its intensity. The frequency bandwidth of the resulting chirped pulse remains the same as that of the corresponding transform-limited laser pulse. The theoretical approach we used to calculate the unperturbed energetic structure of the hydrogen atom is based on an accurate L2 discretization technique using B-spline functions [21,22]. We calculated the ionization probability by numerically solving the three-dimensional time-dependent Schrödinger equation using a spectral method [23-25]. We show how the sign of the chirp parameter induces an asymmetry in the ionization process in the hydrogen atom. We present results of the time evolution of the 1s and 2p bound states population from the switch-on to the switch-off of the chirped pulses and then we analyze the role of the first excited state 2p in the ionization process.
Atomic units 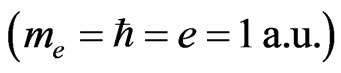 are used throughout the paper unless otherwise mentioned.
are used throughout the paper unless otherwise mentioned.
2. Theoretical Approach
2.1. Atomic Structure Calculations
The time-independent Schrödinger equation (TISE) describing the electron motion around the atomic nucleus is given by:
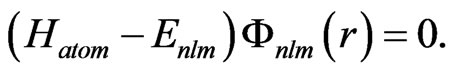 (1)
(1)
Hatom is the non relativistic field-free Hamiltonian in spherical coordinates, which reads
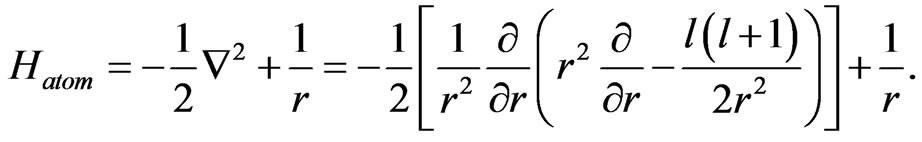 (2)
(2)
For a given electron angular momentum l and projection m, the solution of Equation (1) can be written as follows:
 (3)
(3)
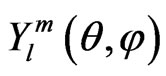 is the spherical harmonic functions depending on angular coordinates. The B-spline function of order k denoted by
is the spherical harmonic functions depending on angular coordinates. The B-spline function of order k denoted by  is a piecewise polynomial of degree k ‒ 1 [20]. We use Nb B-spline functions, that are distributed along the radial axis, in a radial box defined from r = 0 to Rmax. A direct diagonalization of Equation (1) gives the unperturbed eigenenergies Enlm and eigenfunctions of all bound and continuum discretized states. We have proven the efficiency of our discretization technique in previous works on the hydrogen molecular ion and two-active electron systems [23-25].
is a piecewise polynomial of degree k ‒ 1 [20]. We use Nb B-spline functions, that are distributed along the radial axis, in a radial box defined from r = 0 to Rmax. A direct diagonalization of Equation (1) gives the unperturbed eigenenergies Enlm and eigenfunctions of all bound and continuum discretized states. We have proven the efficiency of our discretization technique in previous works on the hydrogen molecular ion and two-active electron systems [23-25].
2.2. Time-Dependent Calculations
Within the electric dipole approximation, the time-dependent Schrödinger equation (TDSE) describing the electron motion in the presence of the laser field is given by:
 (4)
(4)
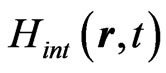 describes the interaction of the electron with the laser field. It could be expressed in different gauges as for example the length or velocity gauges. As we adopt here the velocity gauge,
describes the interaction of the electron with the laser field. It could be expressed in different gauges as for example the length or velocity gauges. As we adopt here the velocity gauge, 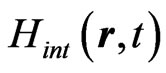 is written as the scalar product of the potential vector and the electron momentum:
is written as the scalar product of the potential vector and the electron momentum:
 (5)
(5)
where  is the vector potential of the chirped laser pulse linearly polarized along the z axis. The timedependent total wave function
is the vector potential of the chirped laser pulse linearly polarized along the z axis. The timedependent total wave function  in Equation (4) is expanded on the basis of the field-free atomic eigenstates, normalized to unity,
in Equation (4) is expanded on the basis of the field-free atomic eigenstates, normalized to unity,
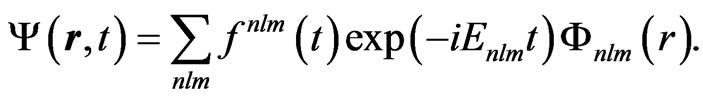 (6)
(6)
By substituting Equation (6) into Equation (4), we obtain a set of coupled integro-differential equations, which we solved using an explicit fifth-order Runge-Kutta numerical method [24].
The vector potential of the chirped laser pulse considered here is given by:
 (7)
(7)
With ξ is the chirp parameter, 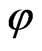 the pulse carrier-envelope phase (CEP), A(ξ) the peak amplitude, ω(t, ξ) the instantaneous frequency and F(t, ξ) the Gaussian time envelope. We note that, in experiment, chirp filters are implemented by use of dispersive optical systems. Upon transmission through a filter characterized by a b chirp coefficient, an initially transform-limited pulse (ξ = 0) becomes chirped, i.e., with frequency ω(t, ξ) that varies in time and depends on the chirp parameter
the pulse carrier-envelope phase (CEP), A(ξ) the peak amplitude, ω(t, ξ) the instantaneous frequency and F(t, ξ) the Gaussian time envelope. We note that, in experiment, chirp filters are implemented by use of dispersive optical systems. Upon transmission through a filter characterized by a b chirp coefficient, an initially transform-limited pulse (ξ = 0) becomes chirped, i.e., with frequency ω(t, ξ) that varies in time and depends on the chirp parameter  (for the experimental details see [26]).
(for the experimental details see [26]). 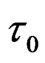 is the full width at half maximum (FWHM) duration of the transform-limited pulse. The filtered pulse will be upchirped if ξ is positive and will be down-chirped if ξ is negative.
is the full width at half maximum (FWHM) duration of the transform-limited pulse. The filtered pulse will be upchirped if ξ is positive and will be down-chirped if ξ is negative.
The expression of A(ξ) is given by:
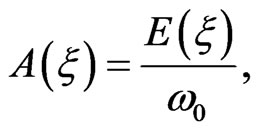 (8)
(8)
where  is the electric field amplitude of the chirped pulse, with
is the electric field amplitude of the chirped pulse, with 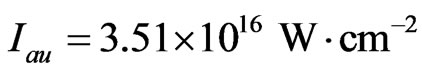 the atomic unit of intensity and ω0 the central carrier frequency. The intensity of the chirped pulse I(ξ) is related to the intensity I0 of the transform-limited pulse by :
the atomic unit of intensity and ω0 the central carrier frequency. The intensity of the chirped pulse I(ξ) is related to the intensity I0 of the transform-limited pulse by :
 (9)
(9)
The instantaneous frequency ω(t, ξ) and the Gaussiatime envelope F(t, ξ) are given, respectively, by :
 (10)
(10)
and
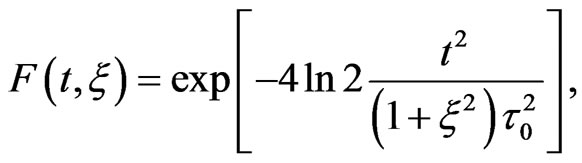 (11)
(11)
The FWHM duration of the chirped pulse is given by:
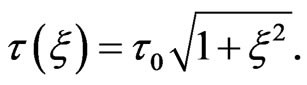 (12)
(12)
During the progress of the laser pulse, the probability of finding the system in the 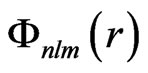 electronic eigenstate at any time t is given by:
electronic eigenstate at any time t is given by:
 (13)
(13)
The ionization probability, at any time t during the laser-atom interaction, is the sum of the population of all the continuum electronic states of positive energy E. It is given by:
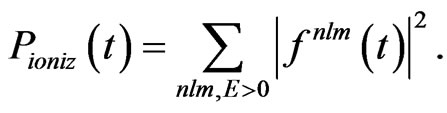 (14)
(14)
3. Results and Discussions
For the numerical calculations, we have considered a set of Nb =1200 B-splines of order k = 7 defined on the radial box of maximum length Rmax = 1000 a.u. We have fixed the maximum electron angular momentum to l = 12. As we choose the laser pulse to be polarized linearly along the z axis, only electronic transitions between states of m = 0 magnetic quantum number are permitted. We kept in all our calculations the CEP constant and set to φ = 0. The convergence of our numerical results has been checked by increasing the number of B-spline functions, the radial box size and the number of angular moment a. We have also checked that the results are gauge independent.
We consider in this paper a transform-limited pulse (ξ = 0) of central carrier frequency ω0 = 0.399 a.u. (10.85 eV), which corresponds to the 7th harmonic of Ti:Sa laser (λ = 114 nm). The pulse has an intensity  and a FWHM duration
and a FWHM duration .
.
We plot, in Figure 1, the transform-limited pulse vector potential 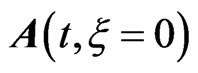 variation with time. In experiment, upon transmission through a chirp filter, an initially transform-limited pulse becomes chirped with a chirp parameter
variation with time. In experiment, upon transmission through a chirp filter, an initially transform-limited pulse becomes chirped with a chirp parameter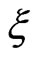 . The filtered pulse will be up-chirped if
. The filtered pulse will be up-chirped if  is positive and will be down-chirped if
is positive and will be down-chirped if 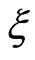 is negative. In Figure 1, we compare between the shape of the
is negative. In Figure 1, we compare between the shape of the  and the vector potentials of a simulated up-chirped pulse of
and the vector potentials of a simulated up-chirped pulse of 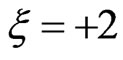 and a down-chirped pulse of
and a down-chirped pulse of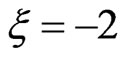 . Both chirped pulses, according to Equations (9) and (12), have an intensity of
. Both chirped pulses, according to Equations (9) and (12), have an intensity of
 and a FWHM duration
and a FWHM duration . The form of the vector potential we use in this paper (see Equation (7)) simulates a realistic experimental case in which the chirp filtering decreases the intensity of the transform limited pulse and increases its to talduration. We present also, in Figure 1, the spectral profile of the three pulses and the variation of their instantaneous frequency
. The form of the vector potential we use in this paper (see Equation (7)) simulates a realistic experimental case in which the chirp filtering decreases the intensity of the transform limited pulse and increases its to talduration. We present also, in Figure 1, the spectral profile of the three pulses and the variation of their instantaneous frequency 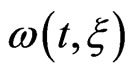 with time. Specifically, an up-chirped pulse (down-chirped) with a positive (negative) value of
with time. Specifically, an up-chirped pulse (down-chirped) with a positive (negative) value of  means that the instantaneous laser frequency increases (decreases) with time. Nevertheless, the frequency bandwidth of the up-
means that the instantaneous laser frequency increases (decreases) with time. Nevertheless, the frequency bandwidth of the up-

Figure 1. Dependence of laser pulse vector potential A(t, ξ), spectral profile and instantaneous frequency ω(t, ξ) on the chirp parameter ξ = −2, 0, +2. The chirped pulses (ξ = ±2) have a central carrier frequency ω0 = 0.399 a.u. (10.85 eV), CEP φ = 0, intensity 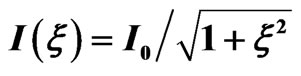 and FWHM duration
and FWHM duration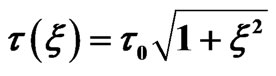 , where
, where 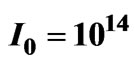 W·cm−2 and τ0 are respectively the intensity and the FWHM duration of the transform-limited pulse of ξ = 0.
W·cm−2 and τ0 are respectively the intensity and the FWHM duration of the transform-limited pulse of ξ = 0.
and down-chirped pulses remains the same that the transform-limited pulse.
We submit the atom taken initially in its fundamental electronic state 1s to each of the three pulses presented in Figure 1. As the energy of the 1s state is , the atom needs to absorb two photons to be ionized. We present, in Figure 2, the results of the ionization probability as a function of the time duration of each of the unchirped pulse
, the atom needs to absorb two photons to be ionized. We present, in Figure 2, the results of the ionization probability as a function of the time duration of each of the unchirped pulse 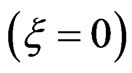 and the chirped pulses of
and the chirped pulses of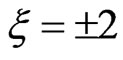 . We notice that the up-chirped pulse ionizes more the atom than both the unchirped and the downchirped pulses. More interesting, the ionization probability obtained at the end of the up-chirped laser pulse is three and a half times higher than that obtained with the down-chirped laser pulse. Figure 2 clearly indicates that the sign of the chirp parameter induces an asymmetry in the ionization yield.
. We notice that the up-chirped pulse ionizes more the atom than both the unchirped and the downchirped pulses. More interesting, the ionization probability obtained at the end of the up-chirped laser pulse is three and a half times higher than that obtained with the down-chirped laser pulse. Figure 2 clearly indicates that the sign of the chirp parameter induces an asymmetry in the ionization yield.
To understand how the sign of the chirp influences the two-photon ionization yield, we analyzed the transfer of the population from the 2p bound state involved in the ionization path to the continuum states. In the present study, the absorption of the first photon by the atominduces a transfer of the population from the fundamental state 1s to the 2p state, whereas the absorption of the second photon results in a transfer of 2p state population to the continuum states. We follow in time the survival population of the 1s state and the amount of the population transferred to the 2p state. We show in Figure 3 (Figure 4) how the 1s (2p) state is depopulated (populated) as each of the three pulses progresses.
We notice from both figures that when the chirped pulses reach their higher intensity, the up-chirped pulse, in contrast with the down-chirped pulse, makes a large amounts of the 1s population transferred to the 2p excited state which considerably depopulates the 1s state and hence enormously populates the 2p sates. Consequently, higher amount of the population is transferred from the 2p bound state to the continuum channel when 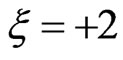 than when
than when . The upand down-chirped laser pulses are of the same intensity and duration, however, the excitation process they induce inside the atom is different. The sign of the chirp parameter influences the variation of the instantaneous frequency
. The upand down-chirped laser pulses are of the same intensity and duration, however, the excitation process they induce inside the atom is different. The sign of the chirp parameter influences the variation of the instantaneous frequency  with
with
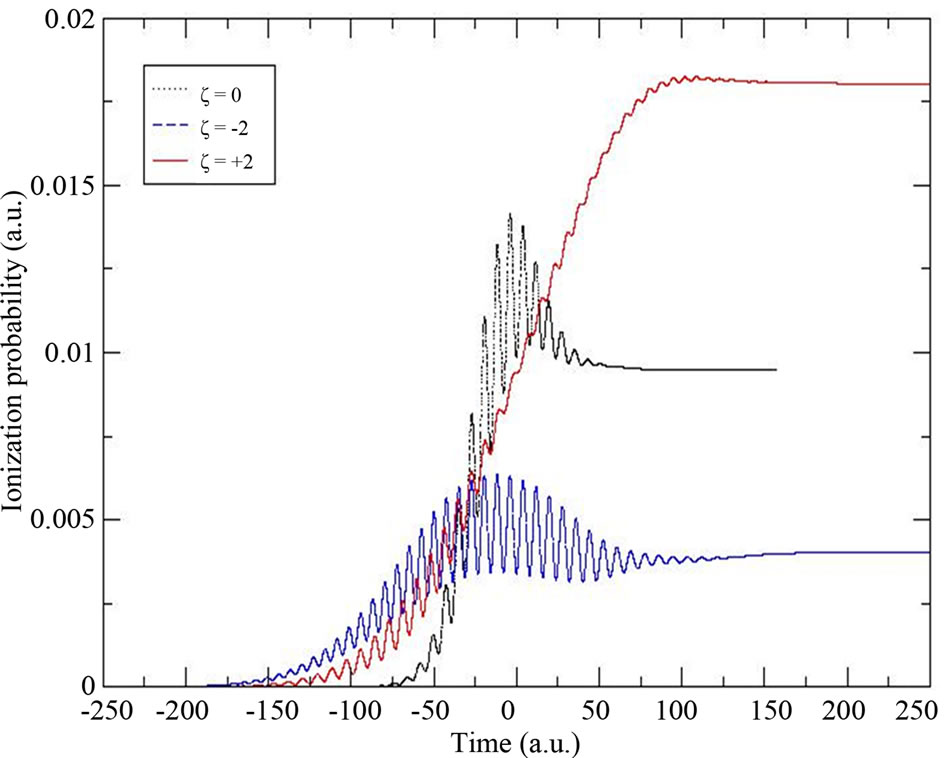
Figure 2. Ionization probability as function of the time duration of the unchirped pulse (ξ = 0) and the chirped laser pulses of ξ = ±2.
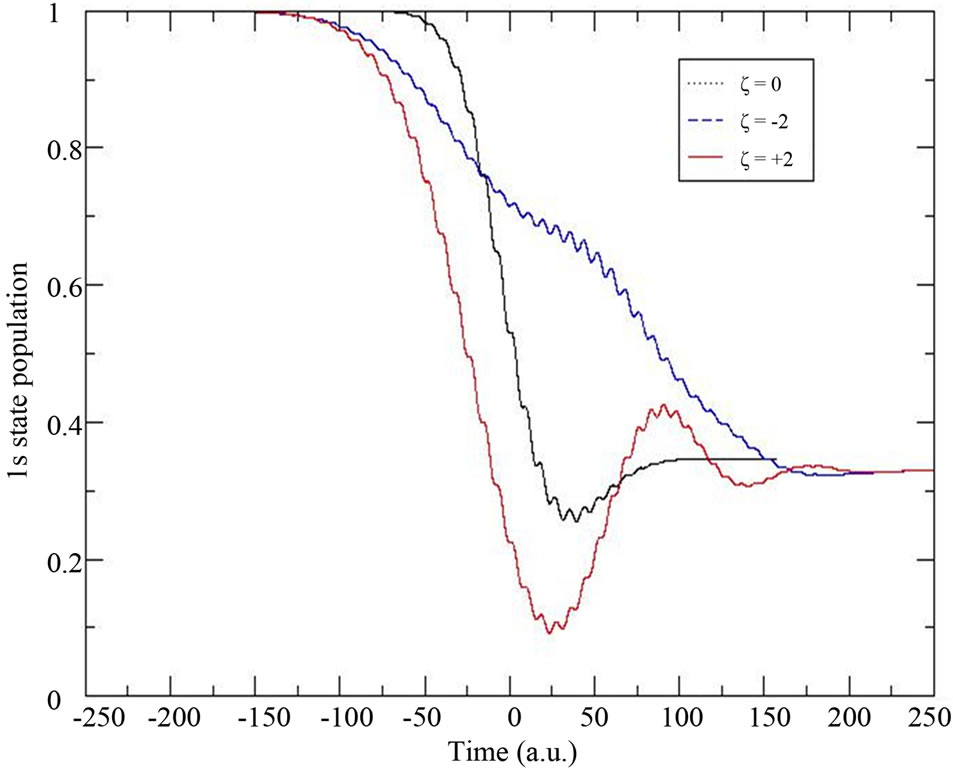
Figure 3. Population of the 1s fundamental state under the unchirped pulse (ξ = 0) and the chirped laser pulses of ξ = ±2.
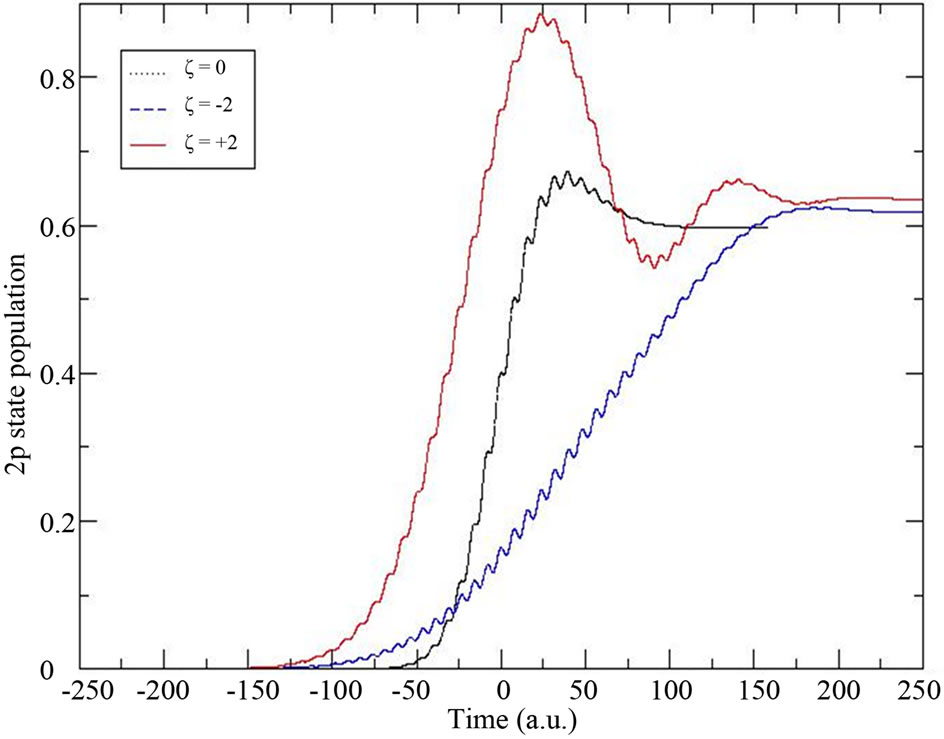
Figure 4. Population of the 2p first excited state under an unchirped pulse (ξ = 0) and the chirped laser pulses of ξ = ±2.
time, which affects the average of the population transferred to the 2p state and then to the continuum states. When the atom is under a chirped laser pulse of a positive , the instantaneous frequency increases as the pulse progresses (see Figure 1). The 2p bound state becomes close to resonance in the first half duration of the laser pulse when the latter is gaining in intensity which reinforces the transfer of the population from the 1s to the 2p state and then to the continuum states. In contrast, when the atom is under a chirped pulse of negative
, the instantaneous frequency increases as the pulse progresses (see Figure 1). The 2p bound state becomes close to resonance in the first half duration of the laser pulse when the latter is gaining in intensity which reinforces the transfer of the population from the 1s to the 2p state and then to the continuum states. In contrast, when the atom is under a chirped pulse of negative , the instantaneous frequency decreases as the pulse progresses. Here, the 2p bound state becomes close to resonance in the second half duration of the pulse when the intensity of the latter is decreasing which weakens the transfer of the population from the 1s to the 2p state and then to the continuum states.
, the instantaneous frequency decreases as the pulse progresses. Here, the 2p bound state becomes close to resonance in the second half duration of the pulse when the intensity of the latter is decreasing which weakens the transfer of the population from the 1s to the 2p state and then to the continuum states.
4. Conclusion
We have numerically investigated in this paper the ionization process in a real hydrogen atom by short and intense chirped laser pulses. We have observed an asymmetry in the ionization yield induced by the sign of the chirp parameter. We found that an up-chirped laser pulse is more efficient to ionize the atom than a down-chirped laser pulse. Our study has proven that chirped laser pulses that are selective are an efficient tool to control the atomic ionization process. The study presented in this paper could be applicable in another atomic or molecular target.
5. Acknowledgements
The present research was supported by the NSERC and by the New Brunswick Innovation Foundation (NBIF). Allocation of CPU time and assistance with the computer facilities from the Atlantic Computational Excellence Network (ACEnet, St-John’s, NL, Canada) and from the “Réseau Québecois de Calcul de Haute Performance” are acknowledged.
REFERENCES
- J. C. Diels and W. Rudolph, “Ultrashort Laser Pulse Phenomenon: Fundamentals, Techniques and Applications on Femtosecond Time Scale,” Academic Press, New York, 1996.
- P. Agostini and L. F. DiMauro, Reports on Progress in Physics, Vol. 67, 2004, pp. 813-855. http://dx.doi.org/10.1088/0034-4885/67/6/R01
- K. Yamanouchi, S. L. Chin, P. Agostini and G. Ferrante, “Progress in Ultrafast Intense Laser Science III,” SpringerVerlag, New York, 2007.
- J. Xu, Physical Review A, Vol. 83, 2011, Article ID: 033823.
- X. Feng, S. Gilbertson, H. Mashiko, H. Wang, S. D. Khan, M. Chini, Y. Wu, K. Zhao and Z. Chang, Physical Review Letters, Vol. 103, 2009, Article ID: 183901.
- F. Krauz and M. Ivanov, Review of Modern Physics, Vol. 81, 2009, p. 163. http://dx.doi.org/10.1103/RevModPhys.81.163
- F. Grossman, “Theoretical Femtosecond Physics: Atoms and Molecules in Strong Fields,” Springer-Verlag, New York, 2008. http://dx.doi.org/10.1007/978-3-540-77897-4
- A. D. Bandrauk, S. Barmaki and G. Lagmago Kamta, Physical Review Letters, Vol. 98, 2007, Article ID: 013001. http://dx.doi.org/10.1103/PhysRevLett.98.013001
- G. L. Kamta and A. D. Bandrauk, Physical Review Letters, Vol. 94, 2005, Article ID: 203003.
- S. Laulan, J. Haché, H. S. Ba and S. Barmaki, Journal of Modern Physics, 2013, in Press.
- V. Prasad, B. Dahija and K. Yamashita, Physica Scripta, Vol. 82, 2010, Article ID: 055302. http://dx.doi.org/10.1088/0031-8949/82/05/055302
- J. Wu, G. T. Zhang, C. L. Xia and X. S. Liu, Physical Review A, Vol. 82, 2010, Article ID: 013411.
- T. Nakajima, Physical Review A, Vol. 75, 2007, Article ID: 053409. http://dx.doi.org/10.1103/PhysRevA.75.053409
- Y. Xiang, Y. Niu and S. Gong, Physical Review A, Vol. 80, 2009, Article ID: 023423. http://dx.doi.org/10.1103/PhysRevA.80.023423
- J. Cao, C. J. Barden and K. R. Wilson, Journal of Chemical Physics, Vol. 113, 2000, pp. 1898-1909. http://dx.doi.org/10.1063/1.481993
- K. J. Schafer and K. C. Kulander, Laser Physics, Vol. 7, 1997, pp. 740-750.
- R. Marani and E. J. Robinson, Journal of Physics B, Vol. 32, 1999, pp. 711-736. http://dx.doi.org/10.1088/0953-4075/32/3/014
- J. Lambert, M. W. Noel and T. F. Gallagher, Physical Review A, Vol. 66, 2002, Article ID: 053413. http://dx.doi.org/10.1103/PhysRevA.66.053413
- C. W. S. Conover, M. C. Doogue and F. J. Struwe, Physical Review A, Vol. 65, 2002, Article ID: 033414. http://dx.doi.org/10.1103/PhysRevA.65.033414
- R. B. Vrijen, D. I. Duncan and L. D. Noordam, Physical Review A, Vol. 56, 1997, pp. 2205-2212. http://dx.doi.org/10.1103/PhysRevA.56.2205
- C. de Boor, “A Practical Guide to Splines,” SpringerVerlag, New York, 1978. http://dx.doi.org/10.1007/978-1-4612-6333-3
- H. Bachau, E. Cormier, P. Decleva, J. E. Hansen and F. Martin, Reports on Progress in Physics, Vol. 64, 2001, pp. 1815-1943. http://dx.doi.org/10.1088/0034-4885/64/12/205
- S. Barmaki, H. Bachau and M. Ghalim, Physical Review A, Vol. 69, 2004, Article ID: 043403. http://dx.doi.org/10.1103/PhysRevA.69.043403
- S. Laulan and H. Bachau, Physical Review A, Vol. 68, 2003, Article ID: 013409. http://dx.doi.org/10.1103/PhysRevA.68.013409
- S. Laulan and H. Bachau, Physical Review A, Vol. 69, 2004, Article ID: 033408. http://dx.doi.org/10.1103/PhysRevA.69.033408
- B. E. A. Saley and M. C. Teich, “Fundamendals of Photonics,” John Wiley and Sons Inc., Hoboken, 2007.
NOTES
*Corresponding author.

