Journal of Modern Physics
Vol.4 No.9(2013), Article ID:36562,5 pages DOI:10.4236/jmp.2013.49157
QCD as High Energy Limit of the Scalar Strong Interaction Hadron Theory
Dragarbrunnsg, 55C, 75320 Uppsala, Sweden
Email: hoh@telia.com
Copyright © 2013 F. C. Hoh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 24, 2013; revised July 26, 2013; accepted August 22, 2013
Keywords: QCD at High Energies; Scalar Strong Interaction; Internal Symmetry
ABSTRACT
This paper is an extension of the book of reference [1] below. QCD Lagrangian is derived from the same equations of motion for quarks used to construct the equations of motion for mesons and baryons in the scalar strong interaction hadron theory that accounts for many basic low energy data not covered by QCD. At high energies, the energetic quarks in a hadron can be far from each other and approximately free. Each quark is associated with a vector in an internal space characterizing its mass and charge. These spaces are interchangeable and provide a new symmetry equivalent to color symmetry in QCD. A quark in a meson has two “colors” and in a baryon three “colors”; the β function of QCD is 61%-92% greater in high energy interactions leading to baryons than that to mesons. This function enters the measurable running coupling constant and this prediction is testable against experiment. QCD, successful at high energies, is thus reconciled with the scalar strong interaction hadron theory and both complement each other.
1. Introduction
The scalar strong interaction hadron theory [1,2] can account, to a limited extent of varying accuracy, low energy hadronic phenomena of basic importance. The high energy end has been left out. Quantum Chromodynamics (QCD) on the other hand, has proven to be successful at high energies but can basically not account for low energy phenomena.
The situation may be summarized in Table 1, which includes the established QED as reference.
In the following, references of the form (x, y, z), Section x.y, §x.y.z, pxyz, and Table x. y refer to those in [1].
QCD is a quantum field theory for “colored” quarks based on the QCD Lagrangian [3 Reviews.../Standard Model.../Quantum Chromodynamics, Equations (9.1, 2)]. The interquark force is of “color” vectorial nature. However, the equations of motion at the quantum mechanical level obtained from the QCD Lagrangian are in terms of unobservable “colored” quarks and are of no use at low energies. This theory has proven to be successful at high energies.
The equations of motion for ground state mesons (2.4.2) and for baryons (9.3.11) form the basis of the present scalar strong interaction hadron theory. There is no quark wave function in these equations and the interquark force is of scalar nature. These equations and the corresponding Lagrangians can be converted into each other. The theory remains largely at the quantum mechanical level and, as mentioned in §6.4.4, has not been quantized.
The wave functions for mesons in (2.4.2) and for baryons in (9.3.11) have been solved for hadrons at rest. In motion, only dimensional estimates for pseudoscalar meson are given in Section 3.5. Feyman propagator for these hadrons is thus not known and Feynman diagrams in an eventual quantized version cannot be evaluated. More basically, the free hadron wave functions in (2.4.2) and (9.3.11) contain via (3.2.3a) in addition to the laboratory coordinate X, also the relative coordinate x as well as the internal coordinate z and u. The latter ones have no correspondence in classical mechanics and the usual transition rule to quantum mechanics is insufficient. This agrees with the known fact that nonlocal thoeries cannot be quantized.
2. Genaralized Equations of Motion for Quarks
The starting point of the scalar strong interaction meson theory [1,2] is a quark A at space-time point xI with flavor p interacting scalarly with an antiquark B at point xII having antiflavor r described by
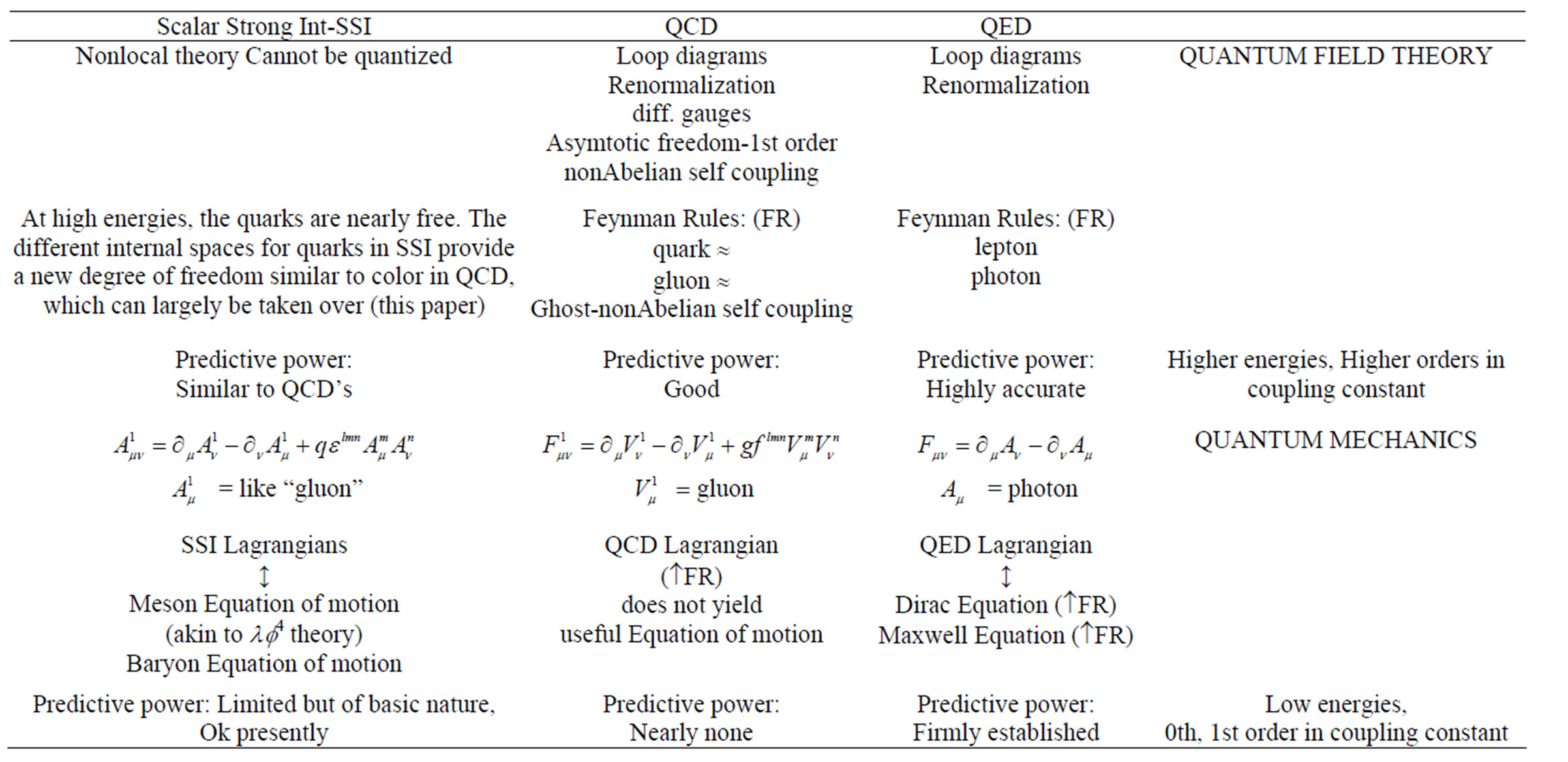
Table 1. Key ingredients in QED, QCD and SSI (scalar strong interaction hadron theory) for comparison.
 (1)
(1)
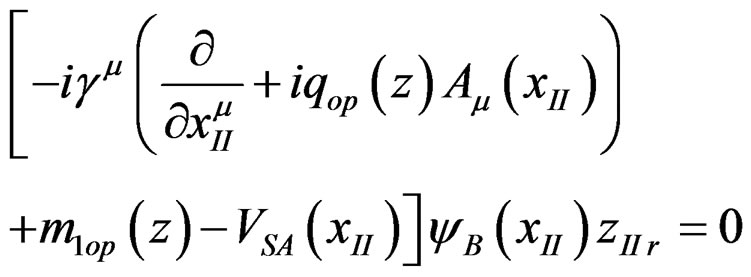 (2)
(2)
In (1) and (2), following the notations of (A1-A5), y is usual Dirac bispinor and VSB(xI) is the scalar potential (2.1.2) emanating from B acting on A and vice versa (2.1.4) for VSA(xII). zp are p complex variables originally providing a point field for implementing SU(p) transformations [4] and zp = (zp)* in (2.3.4). They [2, Section5] acquire here a more physical role as eigenfunctions of the mass operator [2 (9.6a)], (2.3.26)
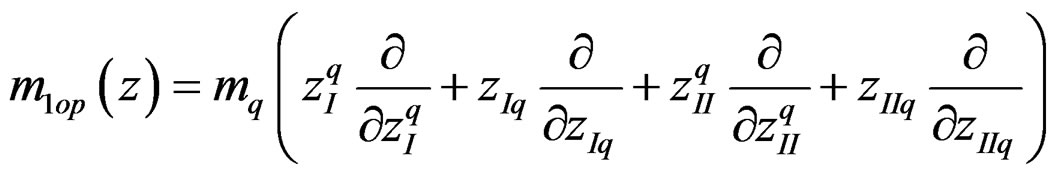 (3)
(3)
as well as the charge operator
 (4)
(4)
generalized from (2.3.14). Repeated indices are summed over. Acting upon zp in (1), (3) and (4) produce the quark mass mp and charge qp, respectively, as eigenvalues. The Am’s are the associated electromagnetic fields. 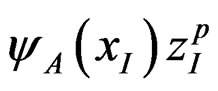 is regarded as the total wave function for quark A and yB(xII)zIIr that of the antiquark B. zI and zII refer to different internal or flavor spaces in Section 2.1 and are as distinct as xII and xI. These z’s, like the relative coordinates x = xII − xI, are “hidden varaiables” in §2.3.5, p. 327. The above equations are taken as hypothetical, as free quark has not been observed, but are used to construct equations of motion for meson. For this purpose, (1) was originally written in van der Waerden’s two spinor form (2.1.1a, 3a) via (2.3.11).
is regarded as the total wave function for quark A and yB(xII)zIIr that of the antiquark B. zI and zII refer to different internal or flavor spaces in Section 2.1 and are as distinct as xII and xI. These z’s, like the relative coordinates x = xII − xI, are “hidden varaiables” in §2.3.5, p. 327. The above equations are taken as hypothetical, as free quark has not been observed, but are used to construct equations of motion for meson. For this purpose, (1) was originally written in van der Waerden’s two spinor form (2.1.1a, 3a) via (2.3.11).
3. Quark Confinement in Meson
The so-constructed equations of motion have been solved for mesons at rest to account for a number of basic problems in the book [1]. After its publication, CP violations in neutral kaon decays have been substantially clarified [5].
The rest frame pseudoscalar meson is confined by the interquark potential (3.2.8a, 19, 20) via the genealization (2.2.3),
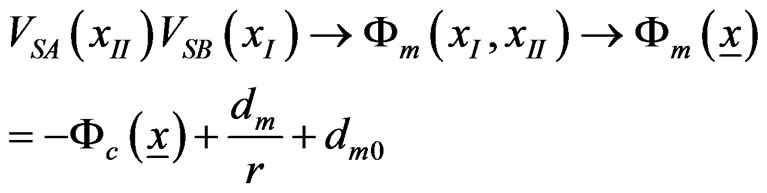 (5)
(5)
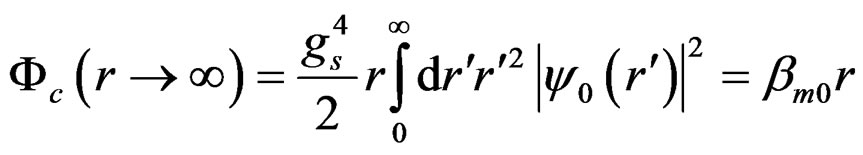 (6)
(6)
where 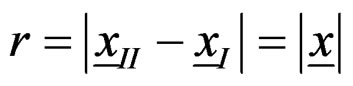 is the interquark distance, dm = 0.864 Gev in (5.2.3), dm0 = 0.24455 Gev2 in Table 5.2,
is the interquark distance, dm = 0.864 Gev in (5.2.3), dm0 = 0.24455 Gev2 in Table 5.2, 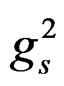 is the scalar strong quark-quark coupling in (2.2.1, 4), and Fc(x) the nonlinear (in y) confinement which provides linear confinement at large r. The meson wave fnnction y0(r) is formed from generalization of the product of yA(xI) in (1) and yB(xII) in (2) according to (2.2.1), satisfies (3.2.10) and is given by (4.3.2)
is the scalar strong quark-quark coupling in (2.2.1, 4), and Fc(x) the nonlinear (in y) confinement which provides linear confinement at large r. The meson wave fnnction y0(r) is formed from generalization of the product of yA(xI) in (1) and yB(xII) in (2) according to (2.2.1), satisfies (3.2.10) and is given by (4.3.2)
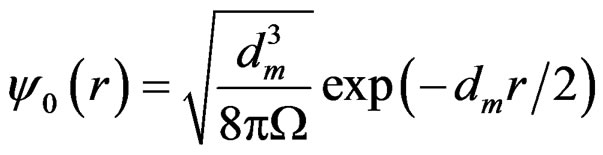 (7)
(7)
where W is a large normalization volume in the laboratory space . For a free meson, W → ¥ and (7) and (6) → 0 and the quarks are confined by dm/r in (5) only. From (7), the size of the meson is about 2 fm in (4.7.3); the quarks are tightly bound.
. For a free meson, W → ¥ and (7) and (6) → 0 and the quarks are confined by dm/r in (5) only. From (7), the size of the meson is about 2 fm in (4.7.3); the quarks are tightly bound.
If the same meson is moving, Section 3.5 shows that its wave function is of the plane wave form  , where E is the energy and K the momentum, and is a four vector in relative space. y0 is the time and large component and the vector part y makes up the spatial and small components. Equations governing these components have not been solved. In addition, the free meson wave function is seen to be nonlocal and can therefore not be quantized.
, where E is the energy and K the momentum, and is a four vector in relative space. y0 is the time and large component and the vector part y makes up the spatial and small components. Equations governing these components have not been solved. In addition, the free meson wave function is seen to be nonlocal and can therefore not be quantized.
For small K, however, approximate forms of y0 and y have been estimated using dimensional approximations and yµK, shown in §3.5.3, 4.
As is discussed in Section 4.5, the above plane wave form is distorted and the corresponding quantity playing the role of W no longer → ¥ when the meson is interacting with another particle. Hence, the wave function becomes finite and the linear confinment (6) is called into action in (5); the quarks are always confined.
At higher energies, the quarks also become energetic and the interquark distance r is expected to be large so that the confining term dm/r in (5) becomes small. In this case, quarks are no longer tightly bound and the nonlinear confinement Fc in (6) can still be weak over a large range of r for large enough W type of volumes. In this r range, Fm in (5) is small and quarks may be considered as approximately free so that (1) and (2) with VSB, VSA → 0 via the left member of (5) are applicable.
4. Internal Space Symmetry and Gauge Transformation
In Section 12.8, on p. 272 at the end of the book, it was pointed out that “The internal degrees of freedom in form of the three internal coordinates zI, zII and zIII of Section 9.3 can play some of the roles of the three colors in QCD...”. This observation will now be pursued and developed. The two internal spaces zI and zII in (1) and (2) are not observables and are interchangeable and thus provide a new symmetry analogous to color symmetry in QCD. Noting this, the total quark wave function 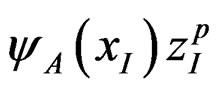 in (1) is generalized to a column matrix with two elements, one with zI the other zII. Consequently, the U(1) gauge field Am must also be generalized to an SU(2) gauge field. The so-generalized (1) and (2) read
in (1) is generalized to a column matrix with two elements, one with zI the other zII. Consequently, the U(1) gauge field Am must also be generalized to an SU(2) gauge field. The so-generalized (1) and (2) read
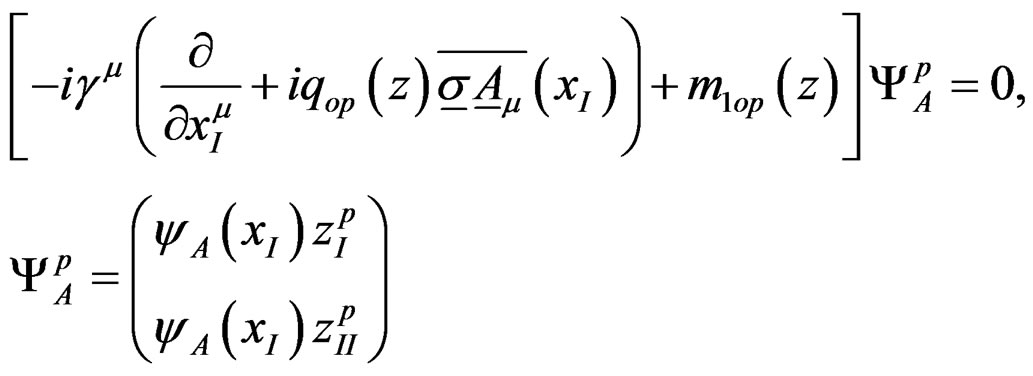 (8)
(8)
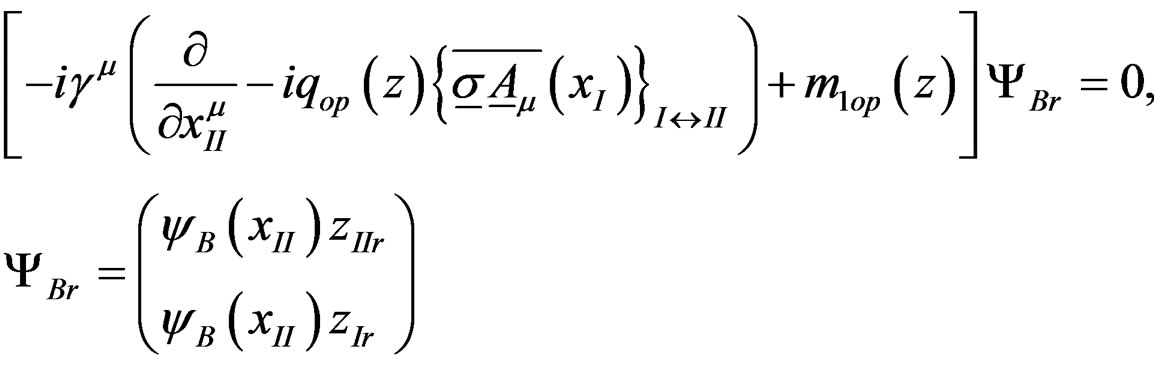 (9)
(9)
observing the definitions
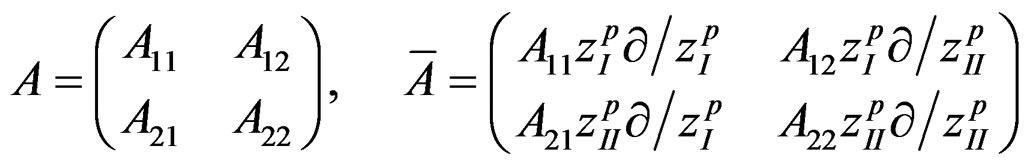 (10)
(10)
The stepping operators of the from zI¶/¶zII has been introduced earlier [6] in connection with the W± bosons. As the`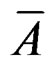 type of matices in (8) and (9) operates on zI and zII,
type of matices in (8) and (9) operates on zI and zII,
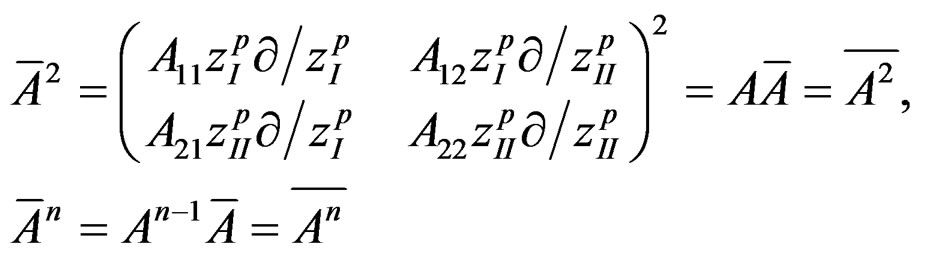 (11)
(11)
because the second order deivatives of the form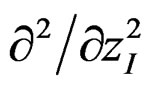 ,
, 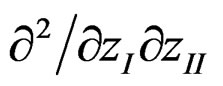 in (11) vanish. Therefore, all higher order deivatives in zI and zII also drop out. Also, zI¶/¶zI and zII¶/¶zII in`A may be dropped without affecting the results.
in (11) vanish. Therefore, all higher order deivatives in zI and zII also drop out. Also, zI¶/¶zI and zII¶/¶zII in`A may be dropped without affecting the results.
Analogous to the usual field tensor [7 (18.8)], define the gauge field tensor
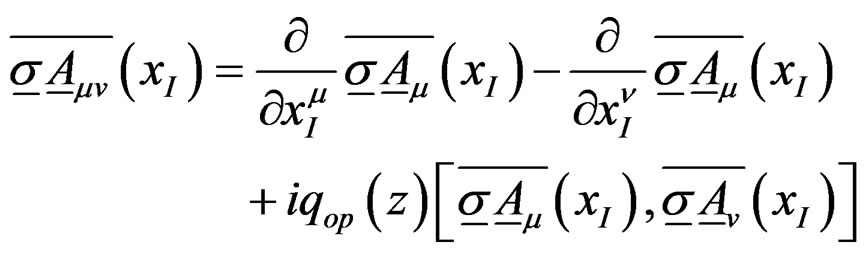 (12)
(12)
Let
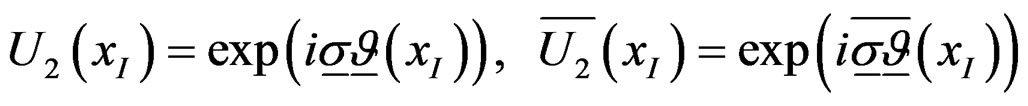 (13)
(13)
Under the SU(2) gauge transformations
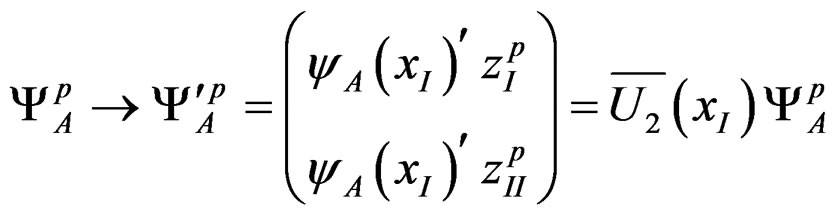 (14a)
(14a)
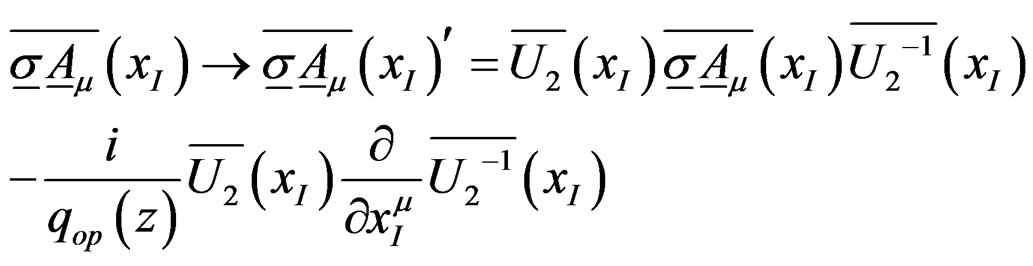 (14b)
(14b)
(8) and (12) are invariant; these invariances are the same as the conventional ones without the z’s in (13) and in (8) and (12), noting that (3) and (4) are invariant under zI « zII and can respectively be replaced by mp and qp. 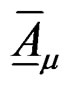 corresponds to the SU(2) gluons in QCD. There are only two degrees of freedom represented by zI and zII corresponding to two colors for quarks in a meson.
corresponds to the SU(2) gluons in QCD. There are only two degrees of freedom represented by zI and zII corresponding to two colors for quarks in a meson.
5. Derivation of QCD Lagrangian
The quark Lagrangian density LQ is obtained by multiplying (8) from the left by  and integrating over the angles in
and integrating over the angles in  and
and . Limiting ourselves to light quarks u, d and s corresponding respectively to flavor p = 1, 2 and 3, which have about the same quark mass mp in Table 5.2, one obtains
. Limiting ourselves to light quarks u, d and s corresponding respectively to flavor p = 1, 2 and 3, which have about the same quark mass mp in Table 5.2, one obtains
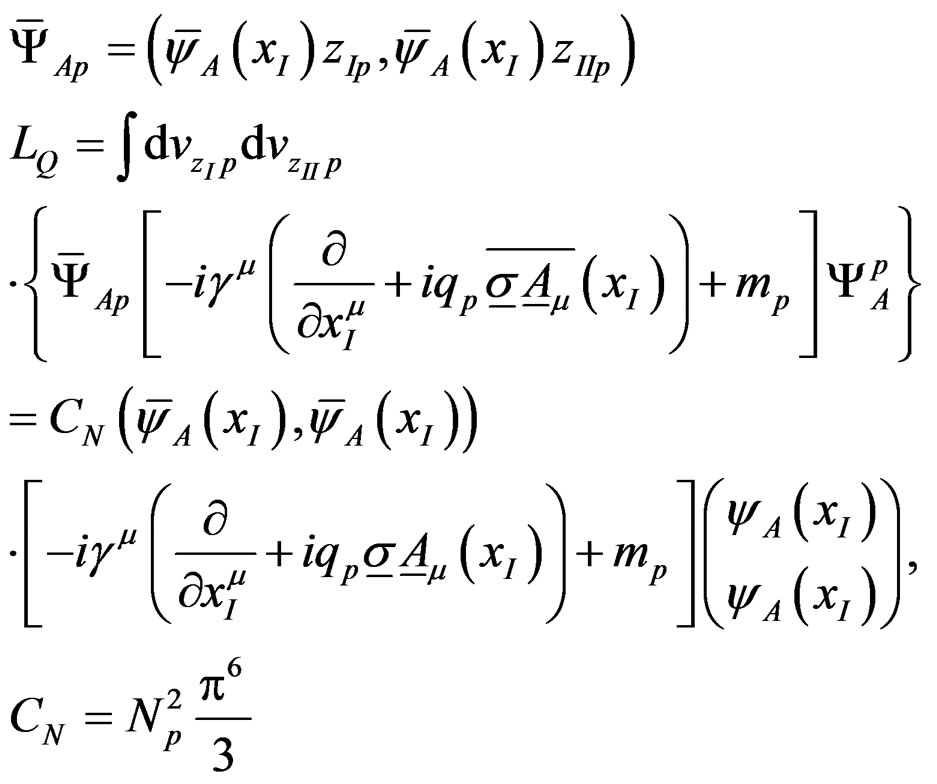 (15)
(15)
Here, (2.3.9, 6b) have been employed and Np is a constant in (2.3.9). The quark charge qp becomes here an unrenormalized coupling constant.
The SU(2) “gluon” Lagrangian density LG is similarly obtained
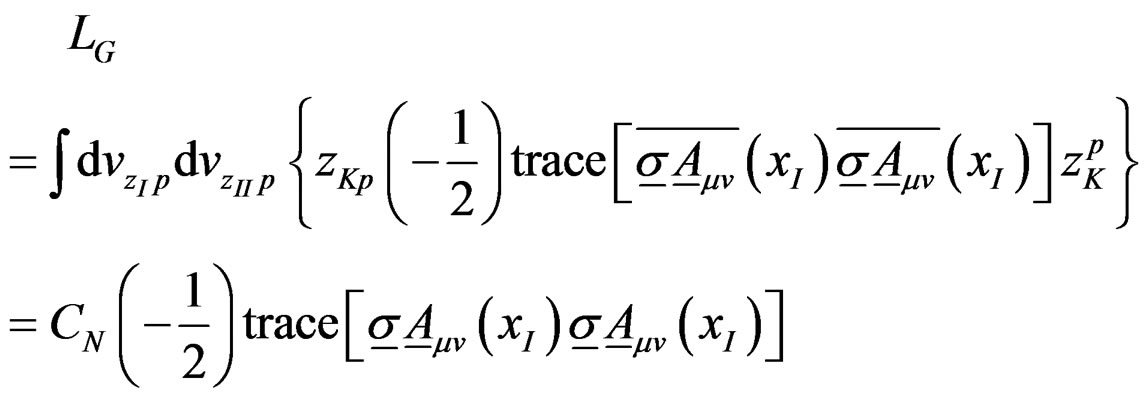 (16)
(16)
where K runs from I to II and (4) has been used in (12). Note that quarks having different “colors” or zK’s have the same space time wave function in (15), as it should. Adding (15) and (16) yields the total “two color” Lagragian density for p = 1, 2 or 3.
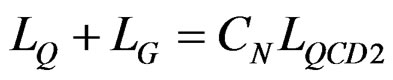 (17)
(17)
The conventional QCD Lagragian density LQCD2 [7, 6 line below (18.6)] for two colors is thus recovered.
The antiqauark Equation (9) can be treated analogously leading to the same results.
Baryon consists of three quarks and makes use of three of (1) associated with three internal spaces zI, zII and zIII in (9.3.1) or three internal degrees of fredom or “colors”. At rest, two quarks merge to form a diquark via (9.2.12) and (9.3.4) and there are only two “colors”. The quarkdiquark confinement potential (10.1.6a, 8) differs from (5) in that db2r2 there provides confinement independent of the nonlinear confinement Fbc(x) there; the quark and the diquark are always confined irrespective whether there is another particle nearby.
When interacting with another particle at higher energies, the quarks also become energetic and the diquark is expected to break up so that there are three interquark distances instead of r. The corresponding form of Fb(x) is unknown but these three distances, like r in high energy mesons, are expected to be large so that the three quarks may be regarded as approximately free in some ranges of the three distances. Again, the nonlinear confinement corresponding to Fbc(x), which provides cubic form of confinement at large r in the quark-diquark configuration (10.2.5b), renders the quarks to be confined. In this case, the above treatment of quarks in meson can straightforwardly be extended to apply to quarks in baryons. The Pauli matrices s above is replaced by the GellMann matrices l and q has now eight components. The conventional LQCD3 [7, 6 line below (18.6)] for three colors is recovered.
The whole development of LQCD2 and LQCD3, including quantization, choice of gauges, renormalization, Feynman rules, asymtotic freedom, etc can be taken over. The QCD beta function µ 11C2-2nf [7 (18.146)] where C2 is 3 for baryon and 2 for meson and the number of flavors nf is 2-5. This function is thus 61%-92% greater in high energy interactions leading to baryons than that to mesons. As this function enters the measurable running coupling constant, this prediction should be testable against experiment.
This effect appears to be effective at large quark separations r for confinement which is taken over by the scalar strong interaction confinement dm/r in (5) and db/r in (10.1.6a) for small r.
In this way, QCD is reconciled with the scalar strong interaction hadron theory and complement each other; the former holds at high energies while the latter accounts for, so far to limited extent of basic nature, data at the low energy end of elementary particle theory. The intermediate energy range remains not covered.
6. On Exact and Broken Symmetry
The known symmetries, C, P, T, and electroweak SU(2) gauge, are all broken. Because they reside in space-time and isospace, the degrees of symmetry breaking can be measured. The SU(2) internal or “color” gauge symmetry here is however exact and cannot be broken. The associated gauge transformation act on two abstract, internal spaces zI and zII, which have been created artifcially [2 Section 5], Section 2.3 to accommodate different quark flavor vectors. These two spaces are identical in structure and there is no quantity in the formalism that distinguish them from each other, i.e., can break this zI « zII symmetry. Even if some such quantity will appear later, it cannot be measured to determine the degree of symmetry breaking because zI and zII are unobservable “hidden” variables mentioned below (4). Such a symmetry breaking would appear as nonexisting. As the “gluons” in (8, 9) depend upon the unobservable quark coordinates xI and xII as well as zI and zII, they can also not be observed.
7. Conclusion
QCD has hitherto been based upon the assumption that a quark has three colors. This has its root in the Pauli exclusion principle. This principle has been confirmed for freely observable fermions; but quarks are not freely observable and hence do not have to obey this principle and the above assumptions become ad-hoc. In the scalar strong interaction theory [1], the quark wave function is generalized to include an internal part in Section 2.3 characterized by zI, and zII in (1) and (2), which is needed to specify its mass and charge via its flavor. It is shown here that this internal degree freedom plays an analogous role as color does in QCD and “justifies” the assumption of colored quarks, with the difference that quarks in mesons have only two “colors”. This difference is testable experimentally. QCD is thus reconciled with the scalar strong interaction hadron theory.
REFERENCES
- F. C. Hoh, “Scalar Strong Interaction Hadron Theory,” Nova Science Publishers, 2011. https://www.novapublishers.com/catalog/product_info.php?products_id=27069
- F. C. Hoh, International Journal of Theoretical Physics, Vol. 32, 1993, pp. 1111-1133. doi:10.1007/BF00671793
- J. Beringer, et al., Physical Review D, Vol. 86, 2012 Article ID: 010001. doi:10.1103/PhysRevD.86.010001
- M. A. B. Bég and H. Ruegg, Journal of Mathematical Physics, Vol. 6, 1965, p. 677 doi:10.1063/1.1704325
- F. C. Hoh, Journal of Modern Physics, Vol. 3, 2012, pp. 1562-1571. http://www.scirp.org/journal/jmp
- F. C. Hoh, International Journal of Theoretical Physics, Vol. 37, 1998, pp. 1693-1705. doi:10.1023/A:1026640524638
- T. D. Lee, “Particle Physics and an Introduction to Field Theory,” Harwood Academic Publisher, 1981.

