Journal of Modern Physics
Vol.4 No.8A(2013), Article ID:36069,9 pages DOI:10.4236/jmp.2013.48A003
Modification of the Newtonian Dynamics in ᴧFRW-Cosmology an Alternative Approach to Dark Matter and Dark Energy
Department of Physics, FACYT, University of Carabobo, Valencia, Venezuela
Email: nelsonfalconv@gmail.com
Copyright © 2013 Nelson Falcón. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 2, 2013; revised July 9, 2013; accepted August 3, 2013
Keywords: Dark Matter; ᴧFRW Cosmology; MoND
ABSTRACT
Modified Newtonian Dynamics (MoND) is an empirically motivated modification of Newtonian gravity at largest scales, to explain rotation curves of galaxies, as an alternative to nonbaryonic dark matter. But MoND theories can hardly connect to the formalism of relativistic cosmology type Friedmann-Robertson-Walker. Presently work intends the existence of one scalar potential, with non gravitational origin, that would solve these problems. This potential Yukawa type inverse is build starting from a specular reflection of the potential of Yukawa: null in very near solar system, slightly attractiveness in ranges of interstellar distances, very attractiveness in distance ranges comparable to galaxies cluster and repulsive to cosmic scales. The consequences of this potential are discussed, through Cosmological Model Tipe Friedmann-Roberston-Walker with cosmological term in function of the distance (lambda like function of r). In the cosmological model so raised the critical density of matter is consistent with the observed density does not include dark matter, MoND theory is deduced for interstellar scales and consequently would explain rotation curves. Also it is shown that Yukawa type inverse does not alter the predictions of the Cosmic Microwave Background neither the primordial nucleosynthesis in early universe; and can be explain the large-scale structure formation.
1. Introduction
The scientific cosmology is based on the description of gravitation by the General Theory of Relativity, more specifically in the solutions of the Friedmann equations for a model of isotropic and homogeneous universe on a large scale (metric Friedman-Robertson-Walker FRW) and continued expansion according to Hubble’s Law. According to this description the dynamics of the universe would be determined by the amount of matter existing in it, which in turn determines the large-scale geometry of space-time.
Recent observations of relic radiation in the Cosmic Microwave Background (CMB) have confirmed in essence the predictions of the Big Bang model and seem to corroborate the predictions of the FRW universe models with zero curvature (k = 0). More refined measures of inhomogeneity in the CMB [1,2] with the measurements of the supernovae (SNe Ia) at high redshift [3,4] suggest the existence of a cosmic acceleration in accordance with the predictions of the model universe with constant cosmological (Λ ≠ 0). This large-scale cosmic acceleration, also called dark energy, is today one of the most important enigmas of modern cosmology [5-7]. Even more disturbing is the apparent contradiction between the models of the universe with zero curvature (k = 0) in the FRW formalism and the total density parameter (Ω), according to which should be exactly equal to unity, but the observed density of matter is an order of magnitude lower than expected to play the null curvature [8].
Assuming that the dynamics of the universe is prescribed only by the force of gravity (as the only fundamental force in the astronomical scales) we encounter serious difficulties in describing the behavior of the Universe:
1) Can not explain the rotation curves of galaxies, which show its incompatibility with the virialized masses of the galaxies [9,10];
2) Into of the rich clusters of galaxies, the mass observed in the form of stars and the gas mass inferred from the X-ray diffuse emission is significantly less than that required to maintain these systems gravitationally stable [8,11];
3) In cosmological scales, the observed baryonic matter density is much lower than predicted by the FRW models with cosmological constant and curvature zero [5-8].
The problem of missing mass appears to affect the dynamics at all length scale beyond the Solar System [12]. One solution has been to propose the requirement of missing material of unknown origin (non baryonic Dark Matter) with equally unknown properties and only interacts gravitationally with ordinary matter. However, after more than a decade of strenuous efforts: theoreticals, astronomical observations and laboratory experiments, only their existence has been suggested conjectural or paradigmatically.
In recent years there have been several alternatives to dark matter paradigm to explain the rotation curves of galaxies, or as alternatives to the TGR and the Big Bang cosmology. Among the first calls include MOND theories, which reproduced successfully the rotation curves of galaxies. But the formalism of the MOND theories 1) can not resolved the lack of dark matter at scales of clusters of galaxies 2) neither the missing masses in the cosmological scale and 3) is based on the modification of the Gravitation Universal Law to scales larger than the solar system, where the dependence of the force of gravity does not necessarily verify the law of the inverse of the square. In the same vein are the Theories of Moffat [13], who postulates a modification of the Universal Gravitation constant, although it is a very promising alternative to the paradigm of Dark Matter, faces problems that a variation of 25% or more in the constant acceleration of gravity would imply an abundance of helium incompatible with the observations [14,15]. Among the proposed changes to the TRG the most promising are those that postulate the existence of an additional scalar field metric tensor (Branks-Dicke theory) [16] and within this socalled quintessence scenarios [17] to postulate a new fundamental interaction, additional to gravity and electroweak interactions (electromagnetic and weak nuclear force) and strong nuclear force.
While it is true that Newton’s law of gravitation, the inverse square law, has been highly supported in the laboratory experiments, to precisions greater than 10−8 for Eötvös-type experiments and spacecraft satellites, there is no experimental evidence to confirm the validity of Newtonian dynamics beyond the Solar System [18,19]. For a review of the many theoretical speculations about deviations from the r–2 law; see Adelberger [20] and references therein. From the very beginning of cosmology and pre-relativistic ideas raised in the modification of gravity beyond the solar system [21-23], but the experiments in laboratories on Earth and in the inner solar system, constitute a strong constraint for any alleged field the anti-gravity with range much greater than 1 AU [21].
In relation to the hypothesis of non baryonic Dark Matter the history of science has shown many examples the paradigmatic assumptions to explain the behavior of the nature, which later were nonexistent and replaced by alternatives measurable. Such as the cycles and epicycles of Ptolemy, the ether before the advent of the Special Theory of Relativity, the “caloric” (as elementary substance) before the work of Joule and Carnot. In all cases, a review of the assumptions in the phenomenological description of the processes, led to a breakthrough in our understanding of natural reality.
We can propose for modification to the theory of gravitation Newton as the Theory MoND, or the modification the General Relativity, as Brank-Dicke (quintessence scenarios), however, consistency is required to connect the new ideas with FRW models [10,24] and the observables of the Big Bang model; such as the acoustic peaks in the CMB fluctuations, the density of matter, the age of the universe in terms of the Hubble constant, primordial nucleosynthesis (baryogenesis) and the formation of structures beginning the primordial fluctuations. In that vein we propose as an alternative to release the assumption that modern cosmology is based, namely that the dynamics of stars, galaxies and clusters of galaxies is determined solely by the force of gravity.
To this end we assume the existence of a new fundamental interaction, whose origin is the baryonic matter, similar to gravity and which acts differently at different length scales, as did the approach of Yukawa for the strong interaction [25]; according to which the nuclear force would be void, attractive or repulsive at different length scales. This new interaction, which we call here Inversed Yukawa Field (IYF) is built by the specular reflection of the Yukawa potential (Section 2), resulting in a cosmological constant depending on the comoving distance, i.e. a null potential near the Solar System, in agreement with the terrestrial experiments, weakly attractive in scales of tens of kiloparsec; consistent with MoND Theory; strongly attractive at scales of tens of Megaparsec, and repulsive in cosmological scales in agreement with the cosmological constant, namely in scales of the order or greater than 50 Mpc.
In this paper, we propose to show that this potential (IYF), built heuristically, leads to a standard FRW model with cosmological constant, in which the density of matter observed is sufficient to verify the flatness (k = 0) without the assumption of the non baryonic dark matter. In Section 3, we will show that a quintessence of the type proposed (IYF) would be concomitant with the observations of CMB, primordial baryogenesis, and solve the horizon problem without the inflationary scenario, and solve the problem of exponential growth of large-scale structures the Universe. Finally, a short discussion and conclusions are shown in the last sections: 4 and 5 respectively.
2. FRW Model with Inversed Yukawa Field (IYF)
Before we assume that any particle with nonzero rest mass is subject to the Newtonian gravitational force by the law of Universal Gravitation, and an additional force that varies with distance, we call the Inverse Yukawa field. Also, without changing the argument, we could be thought that the force of gravitation is bimodal (bigravity): varies as the inverse square of distance scales negligibly small compared to r0, but it varies from very different when the comoving distance is about the kilo parsec or more. In this sense, our story line is a MoND Theory. It is also clear that the origin of this IYF is the baryonic mass like the Newtonian gravitational force.
This potential per unit mass, type Yukawa inverse, is build starting from a specular reflection of the potential of Yukawa [26]: null in ranges very near solar system, slightly attractiveness in ranges of interstellar distances, very attractiveness in ranges of distances comparable to clusters of galaxies and repulsive to cosmic scales:
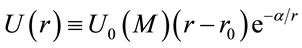 (1)
(1)
where U0(M) is the magnitude of this potencial per unit mass (in units of N/kg) as a function of baryonic mass that causes the field, and r0 is the orden of 50 h–1 Mpc. Where h is the parameter Hubble, defined as 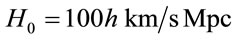 , for the Hubbble constant at the present epoch. Also, α is a coupling constant, in the order of 2.5 h–1 Mpc. The Figure 1 show the variation of U/U0 respect to adimensional variable
, for the Hubbble constant at the present epoch. Also, α is a coupling constant, in the order of 2.5 h–1 Mpc. The Figure 1 show the variation of U/U0 respect to adimensional variable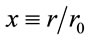 .
.
We can see that in scales of distance, of the order of Solar System, the contribution the this potential is null; is mildly attractive in distances of the order of the kilopar-
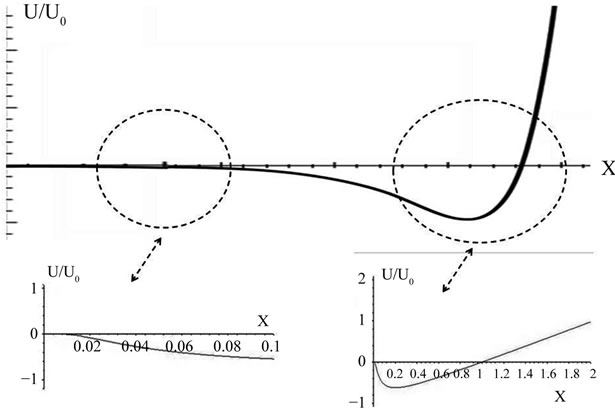
Figure 1. Potential Yukawa Inverse per unit mass as function of adimensional comoving scale x = (r/50 h−1) Mpc. (left: the function near the origin; right: Large-scale variation).
sec, strongly attractive in ranges of distances comparables to megaparsec and repulsive to cosmological scales.
Thus de Yukawa inverse force per unit mass, namely bimodal complement large-scale Newtonian gravitation would be:
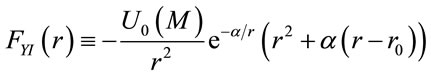 (2)
(2)
Also in the weak field approximation 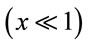 the Yukawa inverse Force per unit mass is given by:
the Yukawa inverse Force per unit mass is given by:
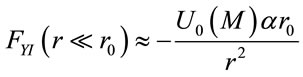 (3)
(3)
But if x→0 this Force per unit mass is null, in accordance to the measures in experiments on Earth.
Now, we prove that (Equation (2)) recovers the MONDMilgrom assumptions, is this for a given mass M, the asymptotic acceleration at r (in order to kiloparsec) goes as r–1 [24,27], Thus r ≈ kpc then
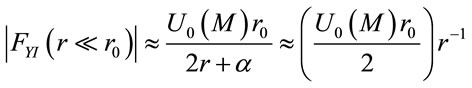 (4)
(4)
This expression is represents in the right side of the Figure 2, where IYF is decreasing. Note that the maximum occurs at a distance of the order to x = 10–2. Furthermore, if MOND theory can explain completely the rotation curves of the galaxies, then the inclusion of the IYF field can too. Remember that the usual Newton law for the gravitation, is adds to this force per unit mass (Equation (4)).
Also, in at cosmological range, the comoving distance, the force Yukawa inverse is constant and provides the asymptotic cosmic acceleration. The minimum value of the potential occurs for:
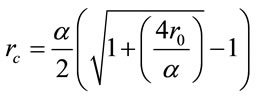 (5)
(5)
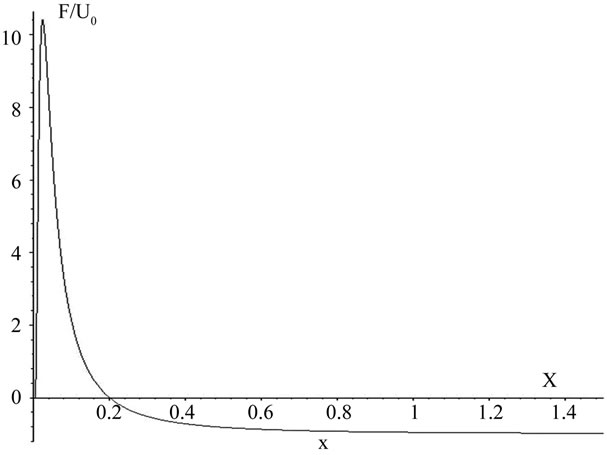
Figure 2. Force Yukawa Inverse per unit mass, as function of adimenssional scale x = (r/50 h−1) Mpc.
If we assume, as before, that α ≈ 2.5 h–1 Mpc and r0 ≈ 50 h–1 Mpc, substituting in Equation (2) we obtain that the maximum value of the force, occurs in the order to Abell radius, for the typical clusters of galaxies, i.e. r ≈ 1.2 h–1 Mpc.
The assumption is justified because r0 it is the average distance between clusters of galaxies [28]. Thus α is calculated in Equation (5) for the average value in the distribution of galaxies, of almost smooth transition to strong agglutination, in the order of rc = 10 h–1 Mpc [5].
Let us now consider a usual homogeneous and isotropic FRW metric with the line element:
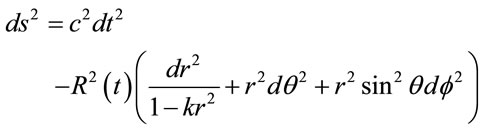 (6)
(6)
where R(t) is the rate of the expansion, gμν is the metric tensor and k = 0, –1, +1 is the scalar curvature for flat, open and closed universe, and c is the speed of light. Also consider a usual energy-momentum tensor for a perfect fluid as:
 (7)
(7)
Now, we assumed that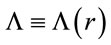 , it is the “force” cosmological, as dynamic variable, respect to the comoving distance. Without loss of generality, we can write:
, it is the “force” cosmological, as dynamic variable, respect to the comoving distance. Without loss of generality, we can write: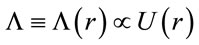 , then
, then
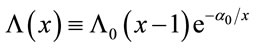 (8)
(8)
where Λ0 is a coupling constant of with dimensions of inverse square meters, and α0 = 1/20 is a dimensionless constant or α0 = α/r0. As before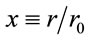 . Then
. Then 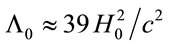 or Λ0 ≈ 0.45 h2 × 10–50 m–2.
or Λ0 ≈ 0.45 h2 × 10–50 m–2.
Thus the Einstein equation with cosmological term is given by:
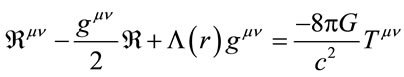 (9)
(9)
where ![]() is the Riemann tensor, and
is the Riemann tensor, and 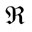 is the Riemann scalar. It’s easy see that the cosmological term leads to usual Friedmann equations (repeating the usual derivation of the equations of Friedmann [29,30], but in the assumption that Λ ≡ Λ(r)):
is the Riemann scalar. It’s easy see that the cosmological term leads to usual Friedmann equations (repeating the usual derivation of the equations of Friedmann [29,30], but in the assumption that Λ ≡ Λ(r)):
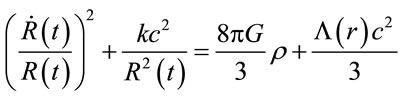 (10)
(10)
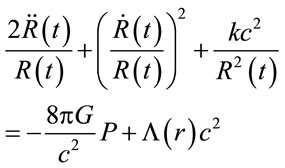 (11)
(11)
3. Cosmological Consequences
But now, the definition of the critical density, change because the potential Yukawa in now nonzero when k = 0. The critical density (ρc), using (Equation (10)) is now:
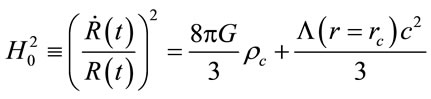 (12)
(12)
Thus the Friedmann equations (Equations (10) and (11)) are:
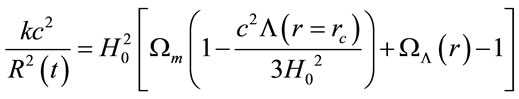 (13)
(13)
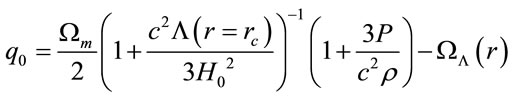 (14)
(14)
where we used the standards notation [31]: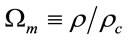 ,
,
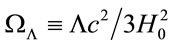 ,
, 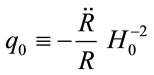 for the dimensionless density parameter of matter, dimensionless cosmological parameter and deceleration parameter respectively. Notice however that ρc is given now by (12). It is easy to see that (13) and (14) carried to the usual Friedmann equations when the Yukawa inverse potential is null.
for the dimensionless density parameter of matter, dimensionless cosmological parameter and deceleration parameter respectively. Notice however that ρc is given now by (12). It is easy to see that (13) and (14) carried to the usual Friedmann equations when the Yukawa inverse potential is null.
Using, as before, 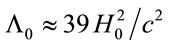 alongside (5) and (8) we obtain
alongside (5) and (8) we obtain
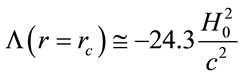 (15)
(15)
The (12) and (15) follows:
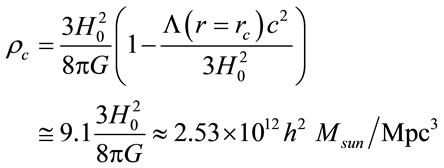 (16)
(16)
Now (Equation (16)) says that increases the value of the critical density parameter, because the critical mass has been underestimated by the usual definition. Thus it has to take to into account the energy of the Yukawa field is in addition to baryonic mass. The mean value of central density value in core of the clusters of galaxies is 3 × 1015 Msun/Mpc3 [32].
Notice that, if we define:
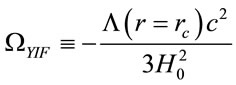 (17)
(17)
And with (15), we obtain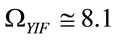 . The Freedman Equations (13) and (14) are:
. The Freedman Equations (13) and (14) are:
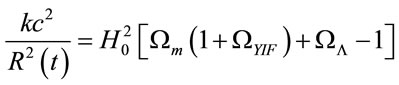 (18)
(18)
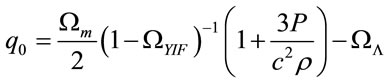 (19)
(19)
But now ΩΛ is a dynamic parameter, using (8) should be evaluated at cosmological scales:
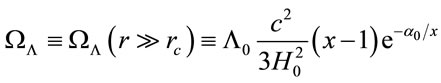 (20)
(20)
For scales larger distances, such as to ensure homogeneity and isotropy, namely at scales larger than 50 h−1 Mpc, or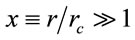 , the behavior of the Λ function is asymptotic (see Figure 1 by
, the behavior of the Λ function is asymptotic (see Figure 1 by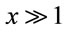 ), and can be estimated as:
), and can be estimated as:
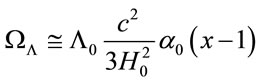 (21)
(21)
Replacing (Equation (15)) into (Equation (21)) with x ≈ 2, equivalent to a comoving distance of the order of 100 h−1 Mpc, range for which the galaxies behave as particles in accordance with a FRW model and the assumptions of homogeneity and isotropy. We obtain:
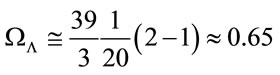 (22)
(22)
very close to the usual value 0.7 [3,4,32].
Now, the remarkable result is that: if k = 0 and ΩYIF ≠ 0 does not require the nonbaryonic dark matter assumption, i.e. using (Equation (15)) and ΩΛ ≈ 0.7 we obtain Ωm ≈ Ωb = 0.03 as the typical value [8,30,33]. for a flat universe model without nonbaryonic dark matter.
For the early stages of the evolution of the Universe, we can find from equations (Equation (13)) and (Equation (14)) the relationship between the scale factor R(t) and the variables of stated: ρ and P; derivative (Equation (13)) to replace d2R/dt2 in (14) and using again (Equation (13)) we obtain, as usual
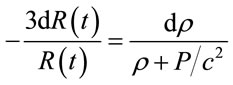 (23)
(23)
Therefore, the dependence of thermodynamic variables density and pressure on the scale factor R(t) remain unchanged and may, as usual, used the state equation 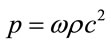 for radiation (ω = 1/3), dust (ω = 0) and vacuum (ω = –1) [31,34]. Similarly neither affects the calculation of time decoupling between matter and radiation.
for radiation (ω = 1/3), dust (ω = 0) and vacuum (ω = –1) [31,34]. Similarly neither affects the calculation of time decoupling between matter and radiation.
The Mattig formula [35,36] only is modified by introducing the critical density term. Using (18) and (21), The Freedman-Lemaitre equation (for the flat universe) is now:
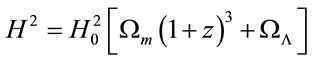 (24)
(24)
Has been omitted for simplicity the contribution of the radiation density, but can be incorporated as a sum, multiplied by the factor (1 + z)4, without loss of generality in the discussion. By flat model (k = 0) we can write the limit the age of the universe at redshift z as:
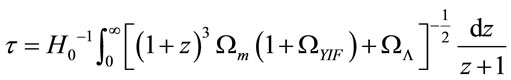 (25)
(25)
Note that if the Yukawa field is zero we obtain the standars equation for the age of the universe in ΛFRW flat model. Using here (Equation (15)), we obtain that the limit of age of the universe, increased by about 30%, until 17 h−1 Gy, because Ωm increased a factor ten.
Remember the problem of the cosmic age associated with the oldest globular clusters in galactic halo and the quasar APM 08279 + 5255 at z = 3.91. If the age estimates of these objects are correct, the puzzle about the cosmic age still remains in the standard cosmology [37- 41], but not in the present model. Also Wang and Zhang [39] suggested that the introduction of any new interaction may be helpful to remove the cosmic age problem and demonstrated that the dark energy paradigm alone, cannot remove the age problem for high redshift.
For the other hand the formation of large-scale structures should be reviewed in the context of a theory of quintessence, as in the case of the inclusion of the inverse Yukawa potential. Since the length of Jeans measuring the dimensions of stability of protogalactic clouds in the form [42]:
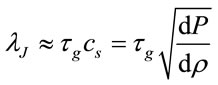 (26)
(26)
where cs is velocity of sound and τg is the free ball time.
To proto-stellar clouds, the time of free fall is only due to the Newtonian gravity, but may not be equal to dimensions higher during times of the early universe, where the dimensions of the clouds would have colossal lengths (proto-galaxies) in scales of megaparsec. At such scales would have bigravity [43,44], and the inverse Yukawa potential, per unit mass, would have to join the force of gravitation. So the length of Jeans is now
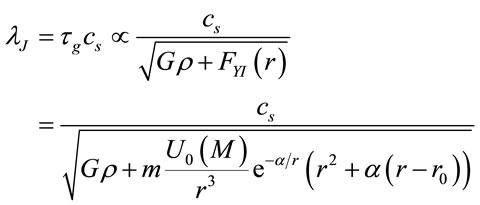 (27)
(27)
Notice that has been used (Equation (2)) as expression of the Yukawa inverse force per unit mass. The additional term is exponential, and could be an interesting approach in the hierarchical fragmentation, also Roos said “there exists no convincing theory of galaxy formation” [45].
The decrease in the Jeans length scale implies that fragmentation could begin in earlier times and consequently favors the formation of proto-galaxies from primordial clouds, whose free fall time is decreases. Also the growth of structure depends the linear contrast of the matter density, and their description is different a different scales [46] as would be expected for a dynamic cosmological term Λ(r). We wish to emphasize the function of linear growth of density perturbations in a flat universe model with cosmological constant has been reported by Eisenstein [47]. If instead of using a constant expression as in Equation (23), is used as a dynamic term (Equation (8)) would be obtained different functions of growth of disturbances at different length scales.
It should be noted that not expected variations in the fragmentation of clouds by the active regions of star formation. Because the dimensions of comoving distances are such that 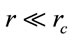 and the term of the inverse Yukawa force is negligible in this case.
and the term of the inverse Yukawa force is negligible in this case.
4. Discussion
The proposed IYF is proportional to the baryonic mass, through the coupling constant U0(M). The particles with zero rest mass, as photons, would not be affected and therefore not expected variations in the CMB. Because of this IYF potential, unlike the force of gravity on the context of general relativity, not cause a curvature in spacetime, in full accord with the hypothesis of Einstein [48] to the propose the cosmological constant, independent of Riemann tensor as in Equation (9).
We can look that the Big Bang nucleosythesis takes place in the early universe, and the baryogenesis calculation [14,49,50] explicitly used Equation (23) which is identical with or without YIF. Other models [13] include scalar fields modified in Newton’s constant of gravitation (G) could be in conflict with primordial nucleosynthesis, which explicitly uses this value compared to the Fermi constant to account for the abundances of light elements observed in the universe. Remark that not the case MoND theory as presented here; for amending the law of gravitation only in distance scales comoving forty orders of magnitude higher than the average distance per nucleon in the primordial plasma.
Another interesting controversy in recent years is that concerning to anomalous acceleration from de Pioneer 10/11 spacecraft when traveling through the outer reaches of the solar system. Indicated the presence of a drift of Doppler frequency, in blue-shift, small and anomalous, interpreted as a sunward acceleration of ap = (8.74 ± 1.33) × 10–10 m/s2 [51,52]. This signal has become known as the Pioneer anomaly; the nature of this anomaly is still being investigated [53,54]. Another possible interpretation of the Pioneer anomaly is to consider the bigravity, For example, if in addition Newtonian gravity, there is a counterpart of the Inverse Yukawa force, as in Equation (3). In this case the coupling constant U0(M) ≡ ξMsun, lest the IYF is proportional to the mass that caused the field. But the (Equation (3)) varies with the inverse square of the distance sun-pioneer, then we assume that average distance between 20 to 70 UA, i.e.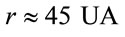 , thus
, thus
 (28)
(28)
Obviously the left side contains the effective force caused by anomalous acceleration (without the Newtonian gravitation acceleration due to sun), and the right side, contains only Inverse Yukawa acceleration for the average value of distance (45 UA). We obtain ξ ≈ 3.337 10−41 N/kg2 and then U0(M) = ξMsum ≈ 6.64 × 10−11 m/s2 This is certainly a very crude approximation but it’s easy to see in Figure 2 that in the range of 20 to 40 UA the IYF varies very slowly and therefore its contribution to the acceleration is almost constant in this range of distance (very small compared with r0).
On the other hand, the missing mass in clusters of galaxies identified by Zwicky [55] to calculate the mass excess using the Virial theorem could easily be resolved without invoking non-baryonic dark matter. Indeed, starting from the Clausius virial expression [56]:
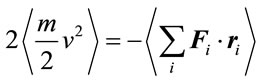 (29)
(29)
But now, the large scale interactions are the Newtonian gravitational force and the Yukawa inverse field, then:
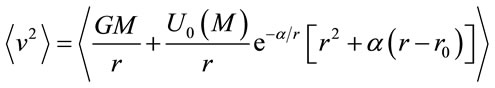 (30)
(30)
Use of the Virial theorem, as Equation (29), only with Newtonian gravity law, implies that the average mass of a star is just the order of the solar mass and average mass of the proto-galaxies is just the mass of the Milky Way [57] in contradiction with our knowledge of the universe and the Copernican Principle, according to which our location is not special in any way. When considering a long-range gravitational interaction, as Yukawa inverse potential, through (Equation (30)) we reverse this paradox.
Also, Mach Principle says that the inertia of an object, is determined as the gravitational interaction with all the distant matter distribution in the universe [58,59]. For some, the Mach principle, which outlines a local connection between inertia and mass distribution on a large scale of the Universe, is more philosophical than scientific because until now all attempts have failed their precise mathematical formulation. The TRG to connect with inertia gravitational fields through the field equations, seem to enter the Mach principle, but not fully verified to be established as the boundary conditions of the Field Equations [23]. The MoND can be interpretation as a new connection between the universe at large and the local inertia [60]. Based on this interpretation, the Yukawa Inverse field can be fully comply the Mach Principle, through of the incorporation of the cosmological term Λ(r), which depends explicitly of cosmological quantities α, ro and rc in the Equations (1)-(4). Certainly it is possible that this cosmological term would also depend on time, in this case the connection with the Higg’s global field can be easy through the cosmological term in the Equations (21) and (22) as the formalism of the Sivaram [61,62].
Ishak [63,64] have shown that the cosmological constant contributes a factor of second order in the angle of deflection from gravitational lenses. It is clear that including the effect of IYF through (21) and (22) also lead to a prediction in the variations of the estimated mass of gravitational lenses using the same estimates.
The origin of the scalar field proposed is beyond the scope of this work, we must bear in mind that there is not still a quantum theory of gravity: Neither have been directly detected gravitons (except perhaps by measurements in the binary pulsar PSR B1913+16 that could be taken as indirect evidence of gravitational waves). There is controversial evidence about the origin of quantum and gravitational phenomena in the literature that are still open and that could justify the existence of a Yukawa type field as proposed [65], also “The existence of an intermediate range coupling to the baryon number or hypercharge of the materials was confirmed.” [66] and Bezerra et al. [67] report “stronger constraints on the parameters of Yukawa-type corrections to Newtonian gravity from measurements of the lateral Casimir force”, also see review by Decca et al. [68]. The cosmological constant can be built through the extended action in the Palatini Lagrangian [69], so the variational formulation YIF field can be made by extension.
5. Conclusions
The traditional way to define the critical density deserves to be rethink, under the action of a scalar field in addition to gravitation (as in model IYF discussed here) is unclear which corresponds to the density of matter in the Einstein-DeSitter Model. A change in the critical density, as in Equation (12) opens up new theoretical possibilities to avoid the paradigm of non-baryonic dark matter.
Have been proposed several modifications to Newtonian gravity, even operating on a large scale or type Yukawa potential [11,13,70-75]. Clearly, the incompatibility between the flatness of the Universe (k = 0) and the density of matter comes from the Friedmann equation in its conventional form, which is removed if it is assumed that the Newtonian gravity act together with some scalar field (bigravity) or within a framework of Modified Newtonian Dynamics, maybe as like the Inverse Yukawa Potential proposed.
Regardless of whether the expression proposed for the so-called Inverse Yukawa force per unit mass, is exactly the proposal here, we see the inclusion of a MoND theory expression through some form of cosmological and dynamic term, i.e. a function of comoving distance as Equations (10) and (11), could be a viable alternative to the paradigm of non-baryonic dark matter and is concomitant with FRW cosmology.
Add a scalar field as the IYF proposed here, or MoND theory that corresponds to a kind of bigravity also imply that the masses of the nuclei of galaxies (Black Holes) have been overestimated, as well as masses as inferred by the gravitational lensing, since the scalar field as summative term, contributes additively in the calculation of the gravitational potential. At large distances from the sources, the reduction in the Newtonian field with the inverse of the square would be offset by an interaction that is growing at much greater distances. These longrange interaction also could be caused by the baryonic mass and therefore would be calculable with usual physics.
REFERENCES
- G. Hinshaw, et al., Astrophysical Journal Supplement, Vol. 180, 2009, pp. 225-245. doi:10.1088/0067-0049/180/2/225
- E. Komatsu, et al., Astrophysical Journal Supplement, Vol. 192, 2011, pp. 1-47. doi:10.1088/0067-0049/192/2/18
- A. G. Riess, et al., Astronomical Journal, Vol. 116, 1998, pp. 1009-1038. doi:10.1086/300499
- S. Perlmutter, et al., Astrophysical Journal, Vol. 517, 1999, pp. 565-586. doi:10.1086/307221
- P. J. Peebles and B. Rastra, Reviews of Modern Physics, Vol. 75, 2003, pp. 559-606. doi:10.1103/RevModPhys.75.559
- P. J. Peebles, “Dark Energy,” In: N. Metcalfe and T. Shanks, Eds., Cosmic Frontiers, ASP Conference Series, Durham University, Durham, 2006, p. 83.
- S. M. Carroll, W. H. Press and E. L. Tunner, Annual Review of Astronomy and Astrophysics, Vol. 30, 1992, pp. 499-542. doi:10.1146/annurev.aa.30.090192.002435
- J. Overduin and P. S. Wesson, “The light/Dark Universe,” World Scientific Publishing, Denvers, 2008.
- Y. Sofue, et al., Astrophysical Journal, Vol. 523, 1999, pp. 136-146. doi:10.1086/307731
- R. H. Sanders and S. McGaugh, Annual Review of Astronomy and Astrophysics, Vol. 40, 2002, pp. 263-317. doi:10.1146/annurev.astro.40.060401.093923
- A. Shirata, T. Shiromizu, N. Yoshida and Y. Suto, Physical Review D, Vol. 71, 2005, Article ID: 064030. doi:10.1103/PhysRevD.71.064030
- K. Freese, Physics Reports, Vol. 333, 2000, pp. 183-201. doi:10.1016/S0370-1573(00)00022-3
- J. W. Moffat, Journal of Cosmology and Astroparticle Physics, Vol. 2006, 2006, Article ID: 001. doi:10.1088/1475-7516/2006/05/001
- H. Reeves, Reviews of Modern Physics, Vol. 66, 1994, pp. 193-216. doi:10.1103/RevModPhys.66.193
- V. N. Melnikov, Frontiers of Physics in China, Vol. 4, 2009, pp. 75-93. doi:10.1007/s11467-009-0008-8
- Y. Fujii and K. Maeda, “The Scalar-Tensor Theory of Gravitation,” Cambridge University Press, Cambridge, 2004. doi:10.1017/CBO9780511535093
- J. M. Martin, Modern Physics Letters A, Vol. 23, 2008, pp. 1252-1265, doi:10.1142/S0217732308027631
- J. H. Gundlach, New Journal of Physics, Vol. 7, 2005, p. 205. doi:10.1088/1367-2630/7/1/205
- M. P. Silverman, General Relativity and Gravitation, Vol. 19, 1987, pp. 511-514. doi:10.1007/BF00760655
- E. G. Adelberger, B. R. Heckel and A. E. Nelson, Annual Review of Nuclear and Particle Sciences, Vol. 53, 2003, pp. 77-121. doi:10.1146/annurev.nucl.53.041002.110503
- I. Goldman, Astronomy and Astrophysics, Vol. 170, 1986, pp. L1-L3.
- H. Seeliger, Astronomische Nachrichten, Vol. 137, 1895, p. 129. doi:10.1002/asna.18951370902
- H. Bondi, “Cosmology,” Cambridge University Press, London, 1951.
- M. Milgrom, Acta Physica Polonica B, Vol. 32, 2001, p. 3613.
- H. Yukawa, Progress of Theoretical Physics, Vol. 2, 1947, pp. 209-215.
- N. Falcon, Revista Mexicana de Astronomía y Astrofísica, Vol. 40, 2010, pp. 11-12.
- M. Milgrom, Proceedings of the Conference. AIP Conference Proceedings, Vol. 1241, 2010, pp. 139-153. doi:10.1063/1.3462627
- L. Guzzo, “Clustering in the Universe: From Highly Nonlinear Structures to Homogeneity,” In: S. Bonometto, V. Gorini and U. Moschella, Eds., Modern Cosmology, Series in High Energy Physics, Cosmology and Gravitation, Institute of Physics Publishing, Bristol, 2002, pp. 344-366.
- S. Weimberg, “Gravitation and Cosmology,” John Wiley and Sons, New York, 1972.
- R. Adler, M. Bazin and M. Schiffer, “Introduction to General Relativity,” McGraw Hill Inc., New York, 1965.
- J. Peacock, “Cosmological Physics,” Cambridge University Press, Cambridge, 1999.
- C. Jones and W. Forman, Astrophysical Journal, Vol. 276, 1984, pp. 38-55. doi:10.1086/161591
- W. L. Freedman, Physics Reports, Vol. 333, 2000, pp. 13- 31. doi:10.1016/S0370-1573(00)00013-2
- P. J. E. Peebles, “Principles of Physical Cosmology,” Princeton University Press, Princeton, 1993.
- W. Mattig, Astronomische Nachrichten, Vol. 285, 1959, pp. 1-6.
- M. Dabrowski and J. Stelmach, Astronomical Journal, Vol. 92, 1986, pp. 1272-1277. doi:10.1086/114261
- F. Pont, M. Mayor, C. Turon, and D. A. Vandenberg, Astronomy and Astrophysics, Vol. 329, 1998, pp. 87-100.
- J. Ma, et al., Astronomical Journal, Vol. 137, 2009, pp. 4884-4896. doi:10.1088/0004-6256/137/6/4884
- S. Wang and Y. Zhang, Physics Letters B, Vol. 669, 2008, pp. 201-205. doi:10.1016/j.physletb.2008.09.055
- R. J. Yang and S. Zhang, Monthly Notices of the Royal Astronomical Society, Vol. 407, 2010, pp. 1835-1841. doi:10.1111/j.1365-2966.2010.17020.x
- S. Wang, X.-D. Li and M. Li, Physical Review D, Vol. 82, 2010, Article ID: 103006. doi:10.1103/PhysRevD.82.103006
- J. Jeans, “Astronomy and Cosmology,” Cambridge University Press, Cambridge, 1928.
- N. Rossi, “Dark Halo or Bigravity?” 2009, [astro-ph.CO], arXiv:0902.0072.
- D. Blas, AIP Conference Proceedings, Vol. 841, 2006, pp. 397-401. doi:10.1063/1.2218199
- M. Ross, “Introduction to Cosmology,” Wiley & Sons Ltd., London, 1997.
- J. B. Sanchez, J. Dent, S. Dutta and L. Perivolaropoulos, Journal of Cosmology and Astroparticle Physics, Vol. 9, 2010, p. 21.
- D. Eisenstein, “An Analytic Expression for the Growth Function in a Flat Universe with a Cosmological Constant,” 1997, [astro-ph.co] arXiv:astro-ph/9709054.
- A. Einstein, Annalen der Physik, Vol. 354, 1916, pp. 769- 822. doi:10.1002/andp.19163540702
- S. Burles, K. Norllett and M. Turner, Astrophysical Journal, Vol. 552, 2001, pp. L1-L5. doi:10.1086/320251
- G. Steigman, Proceedings of the International Astronomical Union, IAU Symposium, Vol. 265, 2010, pp. 15- 22. doi:10.1017/S1743921310000098
- J. D. Anderson, et al., Physical Review Letters, Vol. 81, 1998, pp. 2858-2861. doi:10.1103/PhysRevLett.81.2858
- J. D. Anderson, et al., Physical Review D, Vol. 65, 2002, Article ID: 082004. doi:10.1103/PhysRevD.65.082004
- V. T. Toth, International Journal of Modern Physics D, Vol. 18, 2009, pp. 717-741. doi:10.1142/S0218271809014728
- O. Olsen, Astronomy and Astrophysics, Vol. 463, 2007, pp. 393-397. doi:10.1051/0004-6361:20065906
- F. Zwicky, Helvetica Physica Acta, Vol. 6, 1933, pp. 110- 127.
- H. Goldstein, “Mecánica Clásica,” Reverte, Barcelona, 2000.
- J. A. Gonzalo, “Del Sistema Solar a los Confines del Universo Observable,” In: J. A. Gonzalo, J. L. Sanchez-Gomez and M. A. Alario, Eds., Cosmología Astrofísica, Alianza, Madrid, 1995, pp. 222-247.
- E. Mach, “The Science of Mechanics,” Cambridge University Press, London, 1893.
- G. Singer, Acta Historica Astronomiae, Vol. 27, 2005, pp. 142-161.
- [61] F. Darabi, International Journal of Theoretical Physics, Vol. 49, 2010, pp. 1133-1139. doi:10.1007/s10773-010-0294-5
- [62] C. Sivaram, Astrophysics and Space Science, Vol. 319, 2009, pp. 3-4. doi:10.1007/s10509-008-9952-y
- [63] C. Sivaram and K. Arun, “Dark Energy, Inertia and Mach’s,” 2009. http://arxiv.org/abs/0912.3049
- [64] M. Ishak, W. Rindler and J. Dossett, Monthly Notices of the Royal Astronomical Society, Vol. 403, 2010, pp. 2152-2156. doi:10.1111/j.1365-2966.2010.16261.x
- [65] M. Ishak, Physical Review D, Vol. 78, 2008, Article ID: 103006. doi:10.1103/PhysRevD.78.103006
- [66] C. P. Burgess and J. Cloutier, Physical Review D, Vol. 38, 1988, pp. 2944-2950. doi:10.1103/PhysRevD.38.2944
- [67] E. Fischbach, D. Sudarsky, A. Szafer, C. Talmadge and S. H. Aronson, Physical Review Letters, Vol. 56, 1986, pp. 3-6. doi:10.1103/PhysRevLett.56.3
- [68] V. B. Bezerra, G. L. Klimchitskaya, V. M. Mostepanenko and C. Romero, Physical Review D, Vol. 81, 2010, Article ID: 055003. doi:10.1103/PhysRevD.81.055003
- [69] R. S. Decca, et al., Physical Review D, Vol. 79, 2009, Article ID: 124021. doi:10.1103/PhysRevD.79.124021
- [70] E. Rosenthal, Physical Review D, Vol. 80, 2009, Article ID: 084029. doi:10.1103/PhysRevD.80.084029
- [71] M. White and C. S. Kochanek, Astrophysical Journal, Vol. 560, 2001, pp. 539-543. doi:10.1086/323074
- [72] L. Amendola and C. Quercellini, Physical Review Letters, Vol. 92, 2004, Article ID: 181102. doi:10.1103/PhysRevLett.92.181102
- [73] C. Sealfon, L. Verde and R. Jimenez, Physical Review D, Vol. 71, 2005, Article ID: 083004. doi:10.1103/PhysRevD.71.083004
- [74] S. Reynaud and M. Jaekel, International Journal of Modern Physics A, Vol. 20, 2005, pp. 2294-2303. doi:10.1142/S0217751X05024523
- [75] M. Sereno and J. A. Peacock, Monthly Notices of the Royal Astronomical Society, Vol. 371, 2006, pp. 719-726. doi:10.1111/j.1365-2966.2006.10703.x
- [76] Z. Berezhiani, F. Nesti, L. Pilo and N. Rossi, Journal of High Energy Physics, Vol. 7, 2009, p. 83. doi: 10.1088/1126-6708/2009/07/083

