ABSTRACT

In contrast to the normal operator approach, our reverse approach starts from the state vector in the Hilbert space. In this work, we give a concise introduction to our recent work in this aspect. By postulating a superconducting state (SCS) to be a generalized coherent state (GCS) constructed by pure group theory, we show that some important properties such as the Cooper pairs of the SCS naturally appear in this new framework without resorting to the microscopic origin. This latter characteristic renders this theory a more universal feature in comparison with other theories developed by the operator approach. The studies on the residue of the pair-wise constraint due to the collapse of the GCS lead to a “flat/steep” band model for searching new superconductors.

1. Introduction

The normal approach to understand a physical phenomenon is to study the relevant Hamiltonian of a quantum system, 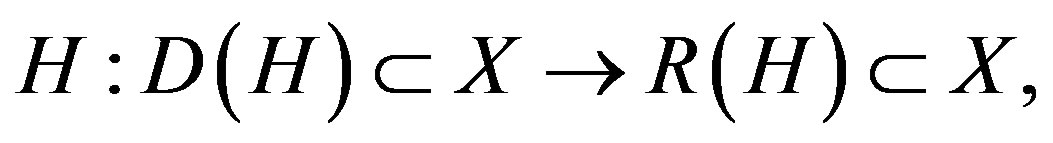where 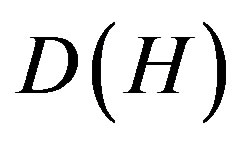and R(H) are the domain of definition and range of H, respectively, X is the complex Hilbert space, Н. This operator approach has its advantage in that the accuracy of the obtained energy by variational method is at least one order higher than its object, i.e. the trial state vector. Moreover if the proposed microscopic Hamiltonian H catches the essentials of the physics, the microscopic mechanism is revealed. However, when facing complicated problems such as superconductivity in high T_c cuprates, iron pnictides, organics etc., the choices of H and D(H) become so controversial that no consensus can be reached until today. On the other hand, this approach provides little help in searching or improving new superconducting materials. Our approach, we call it a reverse approach, starts from the state vector motivated by the coherent character of the superconducting state. This character has long been realized by earlier studies [1,2]. Furthermore, the connection between the Glauber coherent state [3] and the superfluidity as well as superconductivity has also been studied in the framework of “offdiagonal long-range” order and Landau-Ginzburg model, respectively [4,5]. However, a basic problem remains because the construction of Glauber coherent states is based on the boson operators instead of Fermion operators. Also are the Cooper pairs not well-defined bosons due to their very strong overlaps. This problem impeded further development along this line. In this work, we apply the generalized coherent state theory [6] to resolve this problem.

2. GCS for Fermions

The dynamic group of a system consisting of Fermions is decided by the Lie algebra of operators contained in the Hamiltonian as well as the transition operators between different energy levels of the system. A generic Hamiltonian for a many Fermion system can be written as follows,

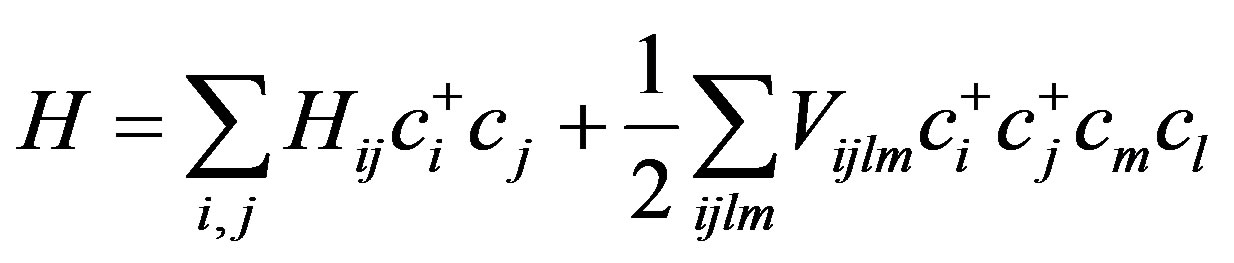(1)

where H_ij=ái|J|jñ, V_ijlm=áij|v|lmñ and J is a single particle operator for kinetic energy, while V_ijlm is the effective Coulomb interaction renormalized by other possible elementary excitations such as phonons etc. The effects of the external field of ionic cores can be included in H_ij. The set of operators, 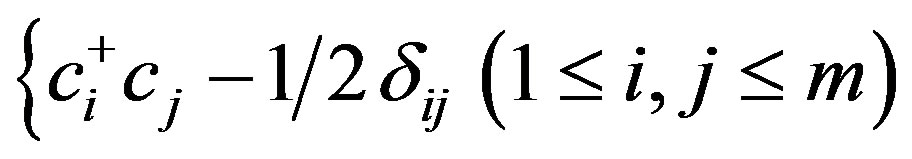, , c_ic_j 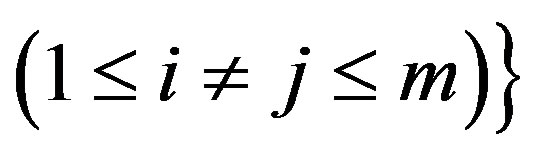span a Lie algebra, ğ, with the Lie bracket defined as the multiplication operation between the elements of ğ: ğ × ğ → ğ. For example,

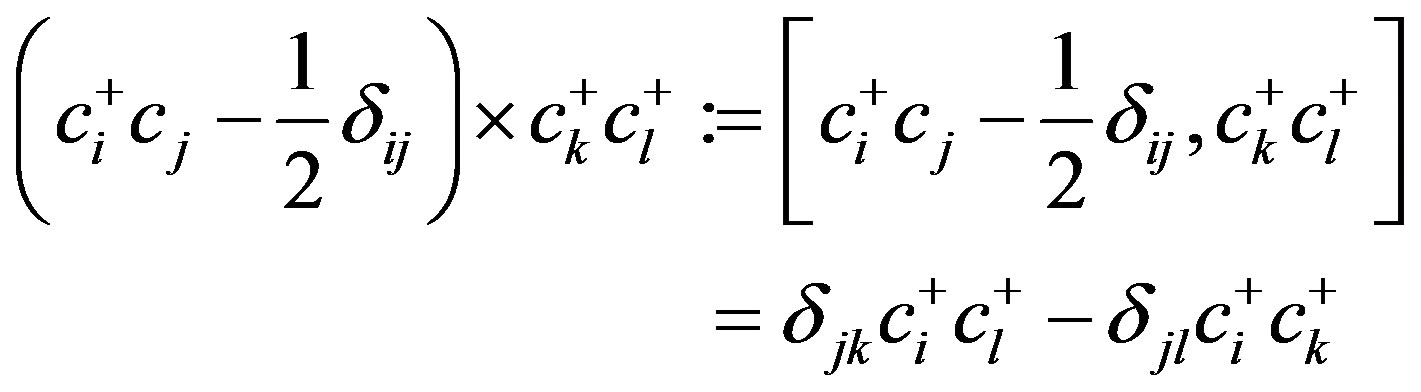(2)

The dynamic Lie group Ğ, of the system described by Equation (1) can thus be constructed by the standard exponentiation procedure of the elements of ğ, i.e. 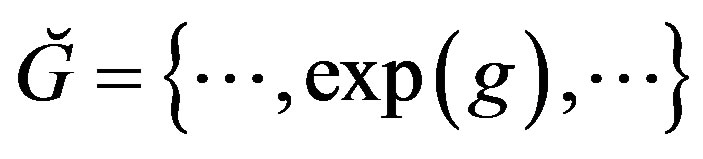for all g ğ. However one should note that the multiplication rule in Ğ is as usual for operators, which is different from that in ğ.

With the knowledge of Ğ, the second step to construct a GCS is to choose a fixed vector, 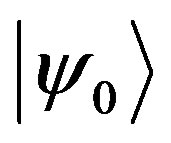, in the Hilbert space, Н. Actually, in the pure group theory approach of Perelomov [6], the choice of 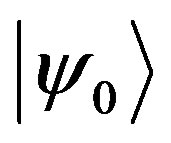is arbitrary. However, as an initial condition this will decides the structure of both GCS and the phase space of the dynamic system. A natural choice for a system with even Fermion modes is to let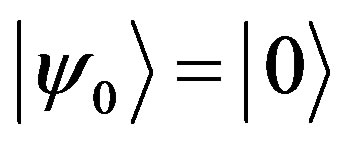, i.e. the vacuum state for Equation (1). Now we consider a subgroup, Њ, of Ğ which acts on as a gauge transformation as follows,

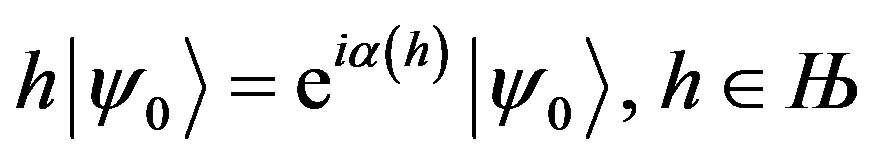. (3)

When Њ is maximal, it is called the isotropy subgroup for the vector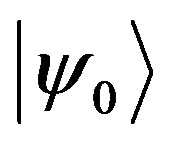. It is obvious that all of the operators in ğ span a subalgebra of ğ, and generate a subgroup of Ğ which satisfies Equation (3), because 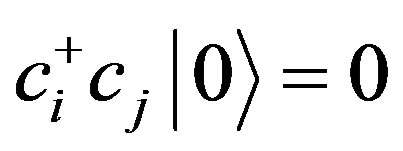. According to group theory, each element g Î Ğ can be uniquely factorized into the product of the element of Њ and the element of the quotient group Ğ/Њ: g = Qh, h Î Њ, Q Î Ğ/Њ. Thus the action of any element g Î Ğ on is given by

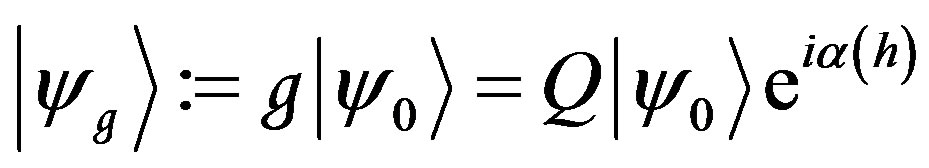. (4)

Equation (4) defines the GCS for an arbitrary Lie group for a dynamic system [6,7]. The essential part in the right side is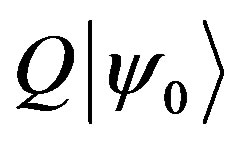, which gives a homeomorphic map between the GCS and the manifold of the quotient group Ğ/Њ. Therefore the GCS preserve all of the topological properties of the quotient group Ğ/Њ manifold.

The explicit form of a GCS, |y_gñ, can be calculated by using a suitable basis for the Lie algebra ğ. For example, for a semisimple Lie algebra the Cartan basis provides a convenient representation for the operators. In the present case, |y_gñ can be represented as the following form in the standard Cartan basis,

(5)

where h_ij are complex parameters and H.c. indicates Hermitian conjugate. It is obvious that the exponential part, T(Q), in Equation (5), is essentially a coset representation of Ğ/Њ. The further simplification of Equation (5) can be realized by using the faithful matrix representation of Ğ/Њ [8,9]. By using the anti-commutation relation of Fermion operators and the Baker-CampbellHausdorff formula, we have shown [10] that the simplified form of Equation (5) is equivalent to the following form,

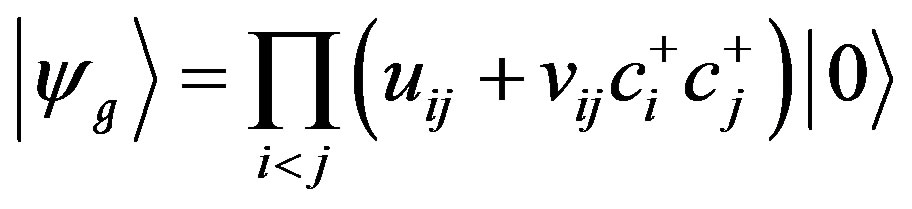. (6)

Equation (6) is formally the same as the BCS wave function [11], if a single particle state is indicated by (k,s). Where k, s indicate the momentum quantum number and spin index, respectively. However, it needs not be so because in our formalism, the sub-index i represents a set of quantum numbers which defines a single particle state. Therefore the GCS approach for the superconducting state is more general, which actually includes both BCS and Bose-Einstein condensation approach for high T_c [12] as a special case. For the latter case, a real space site coordinate should be associated to i, as did in Reference [13]. The pairing of quasi-particles as created by GCS is generally in a Fock space, which sets the necessary condition for superconductivity, while the Cooper pair in BCS theory provided just a sufficient condition. This new pairing is schematically illustrated in Figure 1 for the case of 6 Fermion states system.

The transformation to single particle operators by T(Q) in Equation (5) is shown below,

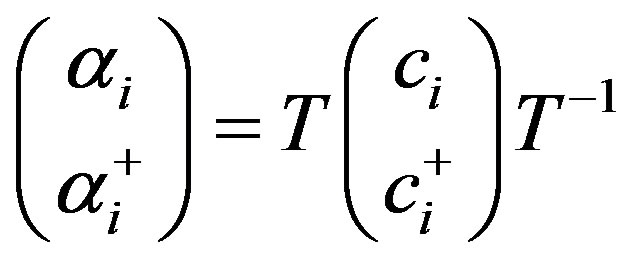. (7)

Within framework of the GCS theory, it can also be shown that Equation (7) is a more general form of Bogoliubov quasiparticle transformation. Therefore the most basic properties for a superconductor can be readily obtained in the framework of GCS theory.

An interesting question is that when the GCS breaks as the system enters into the normal state, whether the pairs still leaves some residue in the electronic structure. This question has been studied in the last few years in the flat/steep band model [13-16].

3. Normal State Characteristics

In the GCS approach, the physical origin for forming the GCS is not explored. However, this question is very important in both basic studies and application aspects. To explore the origin, we need to reverse to Equation (1), the

starting Hamiltonian, to study the characteristics of parameters, H_ij and V_ijlm, for superconducting systems. As required by the GCS condition, it can be expected that for a superconductor, the pairwise constraint for charge carriers should be stronger than that for non-superconductors even in normal state. This signifies smaller group velocities of the charge carriers in the single particle representation for superconductors. This consideration motivates the following Hamiltonian for normal state superconductors [16,17],

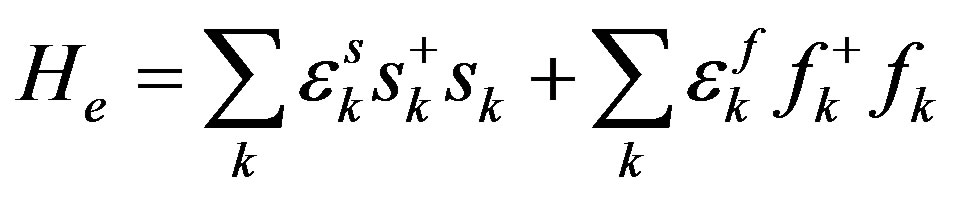. (8)

where s and f refer to steep and flat band, respectively, and the summation index k includes the spin coordinates. This Hamiltonian describes the normal state character of quasi-particles around the Fermi level for superconductors. Two important implications of Equation (8) can be deduced. The first one is the inhomogeneous character of charge carriers in k space. If the electron-phonon coupling dominates the low energy renormalization processes, Equation (8) entails the distinct coupling of steep and flat band electrons with different phonon modes. This manifests itself as a pronounced peak-like structure of electron-phonon(e-p) coupling in electron and phonon phase spaces, a character theoretically predicted before the discovery of MgB₂ (see Reference [13] for a review). In Figure 2, we show our results for Hg and MgB₂ calculated by linear response theory and first-principle method.

The second implication is a two gap structure, an intrinsic property for any two-band model [18]. However, we emphasize that only when the weights of steep and flat band electrons are comparable and there exist no other smearing processes can the two-gap structure be observed, a fact also confirmed in MgB₂.

It should be pointed out that the flatness of a band may be due to other factors such as symmetry, low-dimensionality, and other single particle renormalization of Coulombic or magnetic character. Only pairwise constraints are relevant to superconductivity.

By using an interaction-bipolaron model [16], we have shown that the electronic structures of a large class of metallic material obtained through internal/external doping for the parent covalent insulators. Obviously, the charge carriers in such systems still subject to the pairwise constraint inherited from the parent system, regardless of their phononic or magnetic origin. High-T_c cuprates and Fe-based superconductors are typical such examples. Due to the consideration of pairwise constraint, we attribute the same origin for general pairwise constraint in superconductors and covalency at low energy scale. They divide at higher energy scale, because large covalency occurs for Heitler-London bipolaron, which always leads to localization in a chemical bond. On the other hand, superconductivity can only occur for mobile charge carriers, which sets an upper bound to the pairwise constraint. This unified picture for covalence and pairing of mobile charge carries leads to a prediction initially for diamond [19] and later for all insulators [10]. Namely, “Any covalent insulator when doped into metals by what ever means becomes a superconductor at low temperature”.

4. Conclusion

By applying the GCS theory to study the superconductivity, we have shown that the most important features of superconductors can be easily obtained through pure group theory approach, and the results are more general. As GCS theory is a powerful tool, it can be expected that more interesting results can be obtained with the further studies. The flat/steep band model as motivated by the general pairwise constraint of charge carriers has predicted 1) an inhomogeneous behavior of charge carriers in the momentum space, the origin of pronounced peaklike structure for conventional superconductors; 2) an intrinsic two gap structure; 3) a clue to search new superconductors. Our researches indicate that the flat/steep band condition is fulfilled by the known superconductor from low to High T_c superconductors.

REFERENCES